(1. 同济大学土木工程防灾国家重点实验室,上海 200092;2. 铁道第四勘察设计院集团有限公司,湖北武汉 430062)
摘要 在桥梁延性抗震设计中,群桩基础往往作为能力保护构件进行设计。基于这一设计方法,计算群桩基础的设计地震力时,需要计算承台的地震惯性力。该文建立了承台 - 墩梁两质点模型,分析了承台惯性力随桥墩刚度的变化规律,提出了承台地震惯性力的简化计算公式,以及群桩基础的设计地震力简化计算公式。最后,以实际桥梁工程为背景建立有限元计算模型,通过弹塑性时程分析验证了简化计算公式的正确性和实用性。
关键词 群桩基础,设计地震力,能力保护构件,简化计算方法
中图分类号:U443.15、U442.5
文献标识码:A
文章编号:1009-7716(2011)12-0034-04
Simplified Calculation Formula for Design Seismic Force of Bridge Group Pile Foundation as Capacity Protective Member
Y in Pengcheng, Ye A ijun (34)
Abstract: In the seismic design of bridges ductility, the foundation of group pile is designed as the capacity protective member section es. Based on this design method, it is required to calculate the seismic inertial force of base slab when the design seismic force of the foundation for the group pile is calculated. The article sets up a two-particle model of base slab - pier beam, analyzes the variable rule of the inertial force of base slab with the variation of pier rigidity, and puts forward the simplified calculation formula of seismic inertial force of base slab and the simplified calculation formula of the design seismic force of the foundation for the group pile. Finally, a finite element model based on a practical bridge project is established. The correctness and practicability of the simplified calculation formula is validated by the elastoplastic time-history analysis.
Keywords: foundation of group pile, design seismic force, capacity protective member, simplified calculation formula
0前言
国内外的桥梁抗震设计规范已普遍采用延性抗震思想,并采用能力设计方法进行抗震设计。这一方法的基本思路是,主动选择潜在的塑性铰位置并进行仔细的配筋设计,利用塑性铰的塑性变形延长周期并耗散能力,从而减小地震力,而不希望发生塑性变形的构件,以及脆性的破坏模式则通过提供足够的强度防止其破坏。设置了潜在塑性铰的构件为延性构件,而脆性破坏以及不希望发生非弹性变形的构件,统称为能力保护构件。通过在延性构件和能力保护构件之间建立强度安全等级差异,就可以确保结构充分发挥延性能力,而不会发生脆性的破坏模式。
在桥梁的延性抗震设计中,在选择和设计结构中预期出现的塑性铰位置时,除了应能使结构获得最优的耗能,并尽可能使预期的塑性铰出现在易于发现和易于修复的结构部位外,还应尽可能地减小由于塑性损伤而对结构造成的不利影响。因此,潜在塑性铰位置一般选择设在桥墩上,如单桩墩的墩底、双柱墩纵桥向的墩底和横桥向的墩顶和墩底部位。而群桩基础,如果出现塑性铰既不易检查又不易修复,因此往往作为能力保护构件设计。
作为能力保护构件,群桩基础的设计地震力由桥墩下传的最大地震力和承台自身的地震惯性力两部分组成。严格来说,在地震作用下,桥墩屈服后群桩基础的最大地震内力应通过弹塑性时程反应分析来获得。而且基于能力设计思想,在弹塑性时程反应分析中,桥墩柱潜在塑性铰的截面极限弯矩应当取超强弯矩。但是,这一过程对于工程设计来说过于复杂。在我国现行桥梁抗震规范以及美国桥梁抗震设计规范中,都假定承台的贡献较小,被直接忽略了。实际上,在墩底形成塑性铰后,由于结构动力特性的改变,承台惯性力与弹性阶段相比会发生改变,甚至会增大很多,忽略承台地震惯性力贡献是不合理、不安全的。所以,有必要研究承台地震惯性力的简化计算方法,并进一步得出作为能力保护构件的群桩基础的设计地震力计算方法。
本文针对常规桥梁,首先基于承台 - 墩梁体系的两质点模型分析了墩柱刚度变化对承台惯性力的影响规律,并在此基础上提出了桥墩屈服后承台地震惯性力的简化计算方法,以及作为能力保护构件的高桩承台基础的设计地震力计算方法。然后,根据实际工程结构建立有限元模型进行弹塑性地震反应分析,以验证简化计算方法的合理性和实用性。
1桥墩屈服后承台地震惯性力简化计算方法
1.1规则桥梁两质点模型及其地震反应计算公式
以常规连续梁桥的固定墩为例,此时桥墩的纵向地震反应由一阶振型控制,可以简化为单质点体系进行地震反应计算,于是,承台 - 墩梁结构体系就可以简化为两质点模型(见图 1)。其中,m_1为等效的基础以上桥梁结构质量(包括桥墩),m_2为承台质量,k_1为墩身的水平抗推刚度,k_2为群桩基础的水平抗推刚度,l_1为m_1形心到承台顶的距离,h为承台厚度,P_1和P_2分别为两质点产生的地震惯性力。
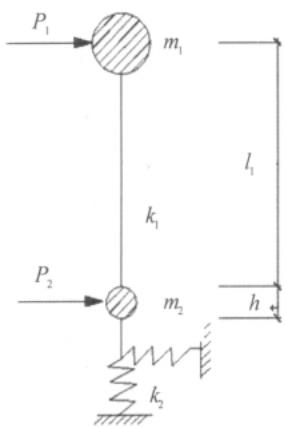
图 1 两质点模型
根据结构动力学基本公式,可得出其两阶振型对应的自振圆频率为:
相应的两阶振型坐标为:
\rho_{11} = \rho_{12} = 1
\rho_{21} = k_{1} / (k_{1} + k_{2} - \omega_{2}^{2}m)
\rho_{22} = k_{1} / (k_{1} + k_{2} - \omega_{2}^{2}m)
根据多自由度系统反应谱计算的振型分解法,各振型的振型参与系数为:
由第 1 振型引起的两质点的最大地震力为:
P_{11} = \gamma_{1}m_{1}a_{1}
P_{21} = \gamma_{1}m_{2}a_{2}\rho_{21}
由第 2 振型引起的两质点的最大地震力为:
P_{12} = \gamma_{2}m_{1}a_{2}
P_{22} = \gamma_{2}m_{2}a_{2}\rho_{22}
上述各式中,a_1, a_2为两阶振型对应的地震加速度反应谱值。
每个振型引起的墩底剪力V_1及弯矩M_1、承台底剪力V_{1}'及弯矩M_{1}'(i = 1,2)分别为:
采用 SRSS 振型组合方法,便可求出各项地震反应:
R即为上面的V_i, M_i, V'_i和M'_i。
1.2桥墩屈服后承台地震惯性力计算公式
对于式(1)中的\omega_1^2和\omega_2^2,当k_1趋向于 0 时,\lim_{k_1\to 0}\omega_1^2 = 0,\lim_{k_1\to 0}\omega_2^2 = k_2 / m_2,即两阶动力特性对应的周期分别趋向于无穷大和m_2单质点的自振周期。
进一步从式 (2) 中可得到,对于振型坐标\rho_{21},当k_1趋向于 0 时,\lim_{k_1\to 0}\rho_{21} = 0,\lim_{k_1\to 0}\rho_{22} = 1。
再根据式 (3),可得到\lim_{k_1\to 0}\gamma_1 = \lim_{k_1\to 0}\left(m_1 + \rho_{21}m\right)/ (m_1 + \rho_{21}^{2}m_2) = 1,\lim_{k_1\to 0}\gamma_2 = \lim_{k_1\to 0}\left(m_1 + \rho_{22}m\right)/ (m_1 + \rho_{22}^{2}m_2) = 1。
作用在m_2的最大惯性力为P_{21}和P_{22}的组合值,即由第一振型和在第二振型在m_2处所引起的地震力组合而成,为表达方便,如果采取绝对值组合,则有:
可见,当h_1趋于 0 或远小于h_2时,两质点模型中m_2的最大地震惯性力近似等于单质点模型的m_2的最大地震惯性力。
通过以上分析可知,当桥墩屈服之后,桥墩抗推刚度远小于基础抗推刚度,甚至可以假设为 0 时,此时上部结构对承台的约束作用非常小,可理想地认为承台 - 墩梁系统的振动就转化为承台系统的单独振动。也就是说,此时承台 - 墩梁系统中承台的惯性力就可以用单承台系统的惯性力来估计,而单承台系统的惯性力可以直接通过反应谱或者线性时程分析得到,计算模型的简化如图 2 所示。
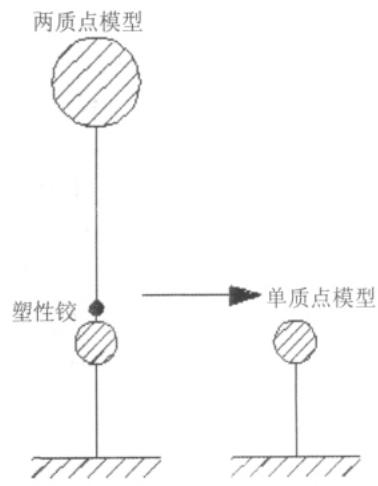
图 2 模型简化示意图
2群桩基础的设计地震力简化计算方法
作为能力保护构件,群桩基础的设计地震力由桥墩下传的最大地震力和承台自身的地震惯性力两部分组成,如图 3 所示。其中,桥墩下传的最大地震力可根据现行规范,按能力设计方法计算,取与桥墩塑性铰区超强弯矩对应的轴力N_p(包括恒载、剪力V_p和M_p弯矩)。而承台的地震惯性力I_{pc}可按前一节的简化公式,采用单自由度反应谱计算,W_{pc}为承台恒载。
忽略地震反应最大值的时间不同步影响,则承台底轴力为墩底轴力与承台重力之和,承台底剪力为墩底剪力与承台惯性力之和,承台底弯矩。
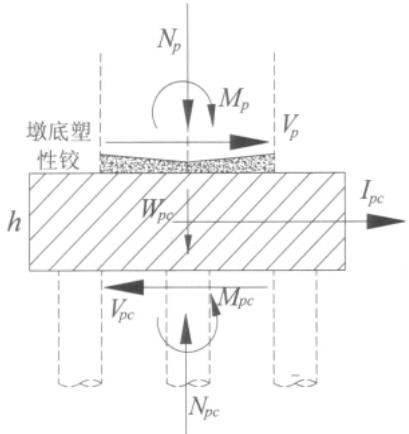
图 3 承台受力示意图
则可以等效为墩底弯矩与墩底剪力及承台惯性力对承台底的作用之和,用公式表示为:
3简化计算方法的实例验证
3.1工程实例及计算模型
选择崇后长江北支大桥引桥(上海段)7 跨50 \mathrm{m}跨径等截面连续梁的固定墩的纵向地震反应作为研究对象。桥墩底截面平面尺寸为5.5 \mathrm{m}\times 2.2 \mathrm{m},墩高15 \mathrm{m},承台厚度2.5 \mathrm{m}。墩身采用 C40 混凝土,基础采用直径为1.6 \mathrm{m}钻孔灌注桩。
建立两个动力计算模型。一个为考虑上部结构质量和桥墩刚度的承台 - 墩梁结构有限元模型。另一个为只考虑承台质量和基础刚度的单承台模型。在承台 - 墩梁结构有限元模型中,桥墩采用 ADINA 程序提供的一种集中塑性单元,即弯矩 - 曲率梁单元来模拟,并考虑了墩底截面的超强系数 1.2,按桥墩截面特性进行离散。弯矩曲率梁单元通过 ADINA 提供的M-\phi多线性弹塑性梁算法,主要采用构件的弯矩一曲率(或扭转角)试验曲线代替其应力一应变曲线参与计算,可以模拟出任意截面的梁单元在外荷载作用下的非线性弹性和弹塑性性能。承台近似按照刚体模拟,墩底与承台中心主从相连。对单承台模型,承台近似按刚体模拟,承台顶,承台中心与承台底主从相连。相关的上部结构质量 5000t 直接加在墩顶,承台质量 500t 则加在承台中心。群桩基础采用六弹簧模型模拟,弹簧刚度根据土层状况和桩的布置形式按静力等效原则确定,土性资料根据 m 法确定,最后得到群桩基础的纵向抗推刚度为 855900kN/m。
3.2地震动输入
在弹塑性时程反应分析中,选用一条人工地震加速度时程和六条实际时程记录作为地震输入。其中,人工地震加速度时程以崇后大桥(江苏段)南引桥 CK6 孔 50a 3% 设防水准的地表加速度反应谱(如图 4 所示)为目标拟合得到。另外六条实际地震记录依次为 ELCentro(1940)、Kobe(1995)、Loma Prieta(1985)、Northridge(1994)、Taft(1952),以及天津波(1976),最大加速度出现时间分别出现在 11.44s、20.92s、12.74s、15.1s、17.26s、7.58s,峰值加速度 (PGA) 根据需要进行一定的调整,以保证桥墩进入塑性且不发生破坏。
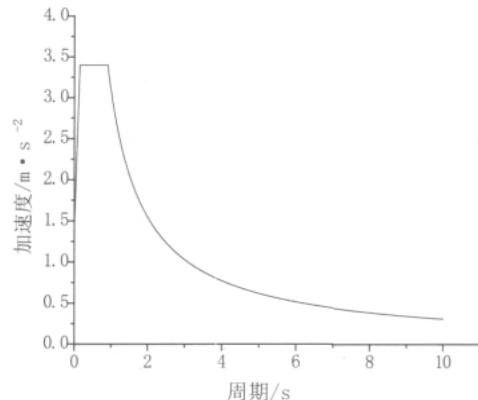
图 4 加速度反应谱
3.3桥墩刚度变化对承台地震惯性力的影响规律分析
在地震动作用下,随着地震加速度的增加,桥梁墩柱截面不断开裂,然后屈服,之后在塑性范围内工作。在这个过程中,桥墩的刚度是不断变化的。以 UCFyber 软件计算出的桥墩底部截面的曲线为依据,将其转化为墩顶的力 - 位移曲线,并计算相应的墩柱刚度的变化情况,可以获得桥梁墩柱在地震动中刚度的变化范围。图 5 为按上述方法得到的 3.1 节中所述桥墩的P-\Delta曲线。
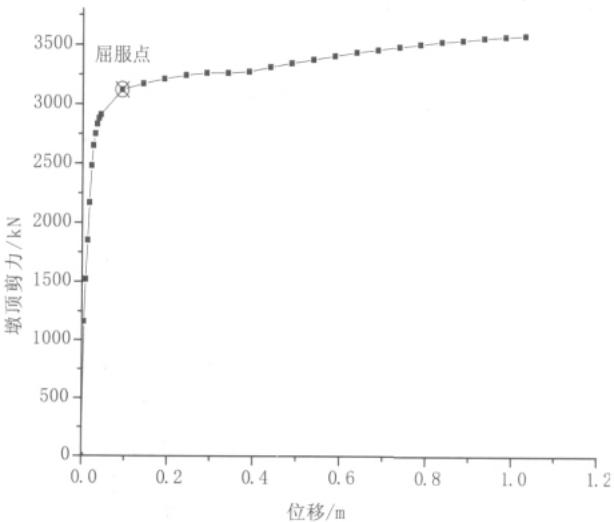
图 5 桥墩P-\Delta曲线图
基于图 5,可得到地震动过程中桥墩的刚度变化情况。进一步地建立了 3.1 节所述固定墩纵向地震反应的承台 - 墩梁结构两质点模型,采用反应谱方法分析随着桥墩刚度变化,承台惯性力的变化规律,并和单承台模型的结果进行了比较。其结果如图 6 所示。
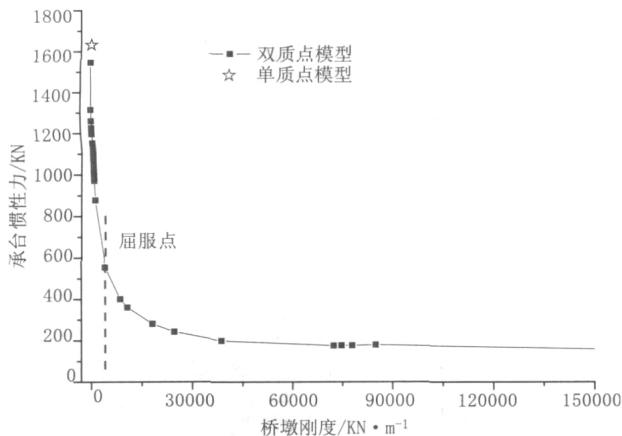
图 6 承台惯性力随桥墩刚度变化的规律曲线图
由图 6 可以看出,随着桥墩截面开裂的不断加剧,刚度不断减小,而承台的地震惯性力则逐渐增加。当桥墩屈服后,桥墩刚度很小,承台惯性力急剧增大,且当刚度趋于 0 时达到最大值,即单承台模型的计算结果。同时可以发现,当桥墩屈服之后,单承台模型可以较好地计算承台反应。
3.4承台地震惯性力验证
采用 3.2 节所述的 7 条地震加速度时程,采用 ADINA 程序,分别对承台 - 墩梁有限元模型和单承台模型进行了时程反应分析。
表 1 列出了两个模型的计算结果比较,由于两个模型的承台质量是相同的,所以直接列出加速度结果。从表 1 中的结果可以看出,承台 - 墩梁结构模型与单承台模型相比,承台的绝对加速度结果吻合的非常好,两者最大误差为6.71\%,平均误差为3.16\%。因此,用单承台模型的惯性力的最大值代替桥墩进入塑性后承台 - 墩梁模型中承台惯性力的最大值,在实际运用中是完全可行的。
表 1 承台绝对加速度计算结果比较一览表
| 地震动输入 | 弹塑性时程分析/m·s² | 简化方法/m·s² | 误差/% | 最大误差/% | 平均误差/% |
|---|---|---|---|---|---|
| 人工波 | 2.819 | 2.841 | 0.78 | ||
| EL Centro | 3.591 | 3.785 | 5.49 | ||
| Kobe | 3.2 | 3.212 | 0.38 | ||
| Loma Prieta | 5.219 | 5.353 | 2.57 | 6.71 | 3.16 |
| Northbridge | 5.779 | 5.572 | -3.58 | ||
| Taft | 3.518 | 3.282 | -6.21 | ||
| 宁海天津波 | 3.926 | 4.031 | 2.67 |
注:误差=(简化方法 - 弹塑性时程分析)/ 弹塑性时程分析,最大误差为误差的绝对最大值。平均误差为误差绝对值的平均值。
3.5群桩基础的设计地震力验证
采用 3.2 节所述的 6 条实际地震加速度记录,采用 ADINA 程序,对承台 - 墩梁有限元模型进行弹塑性时程反应分析,考虑桥墩底截面的超强弯矩影响,可直接得到承台底的地震剪力和弯矩最大值。
而另一方面,采用本文的简化计算方法,按第 2 节中的计算公式,计算桥墩底截面的超强弯矩及其对应的剪力,并叠加承台的地震惯性力贡献,也可得到承台底的设计地震力。
表 2 对采用两种方法的计算结果进行了比较。从表 2 中的结果可以看出,根据简化计算方法得到的群桩基础设计地震力比直接按弹塑性时程反应分析的地震力相比较大,六条地震加速度时程的结果,地震剪力的最大误差为20.64\%,平均误差为14.74\%,而地震弯矩的最大误差为12.57\%,平均误差为6.39\%。相对于承台惯性力而言,承台底地震力的误差更大一些,这主要是因为简化方法忽略了桥墩下传的最大地震力与承台最大地震惯性力在时间上的不同步性。
表 2 群桩基础设计地震力比较一览表
| 地震波 | 反应分量 | 弹塑性时程分析/kN | 简化方法/kN | 误差/% | 最大误差/% | 平均误差/% |
|---|---|---|---|---|---|---|
| EL Centro | 剪力 | 4 991 | 5 442 | 9.03 | ||
| 弯矩 | 62 201 | 64 490 | 3.68 | |||
| Kobe | 剪力 | 4 549 | 5 156 | 13.32 | ||
| 弯矩 | 59 913 | 64 132 | 7.04 | |||
| Loma Prieta | 剪力 | 5 330 | 6 226 | 16.81 | ||
| 弯矩 | 61 232 | 65 470 | 6.92 | |||
| Northbridge | 剪力 | 5 516 | 6 336 | 14.85 | 20.64 | 14.74 |
| 弯矩 | 58 280 | 65 607 | 12.57 | 6.39 | ||
| Taft | 剪力 | 4 560 | 5 191 | 13.81 | ||
| 弯矩 | 61 946 | 64 176 | 3.60 | |||
| 宁海天津波 | 剪力 | 4 613 | 5 565 | 20.64 | ||
| 弯矩 | 61 857 | 64 644 | 4.50 |
注:误差=(简化方法 - 弹塑性时程分析)/ 弹塑性时程分析,最大误差为误差的绝对最大值。平均误差为误差绝对值的平均值。
总体看来,使用简化方法得出的群桩基础设计地震力是偏于保守的,有一些误差,但考虑到地震荷载具有很强的随机性,这样的误差在工程上是完全可以接受的。
在实际桥梁基础的设计地震力计算中,承台的地震惯性力最大值可以采用单自由度反应谱计算,所以不需要进行时程反应分析,手算就可以解决(下转第 42 页)。
不变,由此可以看出塔梁间连接刚度的增大对斜拉桥在横向地震动作用下墩底弯矩影响很小。
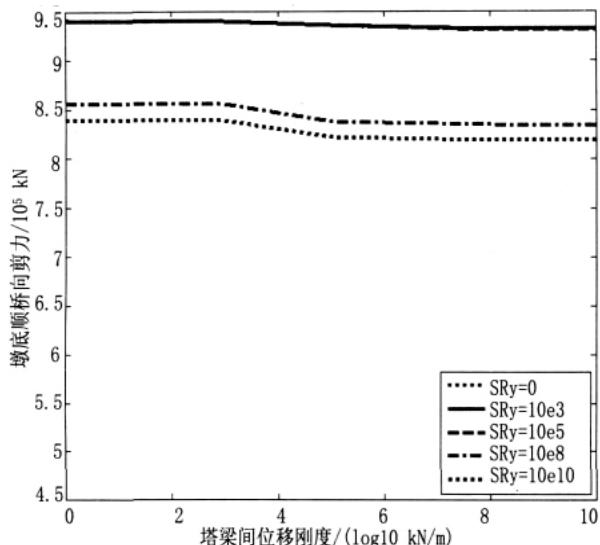
图 9 在顺桥向地震动作用下墩底弯矩 My
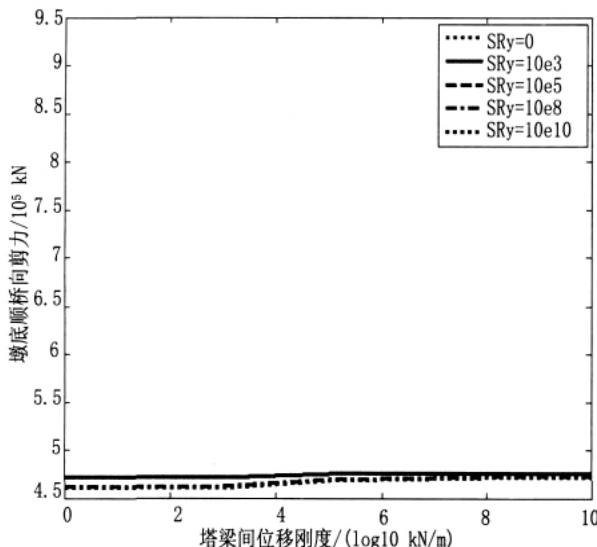
图 10 在横桥向地震动作用下墩底弯矩 Mx
综上所述可以看出,随着塔梁间连接刚度的增加可以有效控制主塔的纵向位移及其塔底弯矩,而对于主塔横桥向塔顶位移及墩底弯矩并没有起到很好的作用,因此在横桥向建议增加主塔刚度限制主塔塔顶位移。
4结论
本文对唐山市津塘运河滨河北大街钢混组合梁斜拉桥在不同塔梁连接刚度下的地震响应进行计算,通过计算发现在顺桥向地震动作用下随着塔梁间的连接刚度的增加,斜拉桥塔顶顺桥向位移逐渐减小,墩底弯矩逐渐降低,墩底剪力基本不变。而在横桥向地震动作用下随着塔梁间的连接刚度的增加,斜拉桥塔顶横桥向位移基本不变,但是塔顶位移比在顺桥向地震动作用下的塔顶纵向位移大了 1.5 倍,所以应增大主塔横向刚度,限制其塔顶位移,墩底剪力及弯矩基本不变。由此可以看出,对于该钢混组合梁斜拉桥可以在塔梁连接处采用塔梁固结形式,采用此种塔梁连接形式不但使结构的受力得到改善,而且省去了主梁在塔梁连接处的支座,使斜拉桥塔梁连接形式得到简化。因此,本文建议该斜拉桥可以采用塔梁固结形式,并增大主塔在横桥向的刚度来限制在横桥向地震动作用下的塔顶位移。