机器学习驱动的砂土场地冲刷桥梁群桩基础地震耗能机制高效识别与分析方法
期刊论文

机器学习驱动的砂土场地冲刷桥梁群桩基础地震耗能机制高效识别与分析方法

王靖程 ^{1,2} , 叶爱君 ^{1,2} , 王晓伟 ^{1,2} , 周连绪 ^{3}

(1. 同济大学土木工程防灾减灾国家重点实验室，上海 200092；2. 同济大学桥梁工程系，上海 200092;
3. 英属哥伦比亚大学工程学院，基洛纳，加拿大，BC V1V 1V7)

摘要：河床冲刷会导致桥梁的地震易损部位从桥墩向群桩基础转移，增加了传统能力保护设计策略的实施成本与难度，因而利用群桩基础耗能的抗震设计成为一种潜在的替代策略。冲刷桥梁群桩基础的地震耗能机制主要分为三类，即摇摆耗能、塑性耗能、以及摇摆 - 塑性共同耗能。对于不同土性、冲刷深度、结构参数的群桩基础，准确、高效地识别它们的地震耗能机制是开展冲刷桥梁抗震设计的前提，然而，传统的群桩基础非线性地震行为分析依赖复杂的有限元模拟，且常伴有计算收敛性问题。为此，本文提出了一种机器学习驱动的砂土场地冲刷桥梁群桩基础地震耗能机制高效识别与分析方法。利用经试验验证的有限元分析方法和随机抽样技术建立了冲刷桥梁群桩基础地震耗能机制数据集，采用经优化的支持向量机、神经网络、以及集成树算法，建立了机器学习驱动的地震耗能机制高效识别和分析模型。结果表明，神经网络能更准确地识别冲刷桥梁群桩基础的地震耗能机制，查准率和查全率基本均超过 90\% ；桩排数、桩长、桩配筋率、墩高以及桩轴压比是冲刷群桩基础地震耗能机制识别的重要变量；桩排数、桩长、桩轴压比越小，桩配筋率、墩高越大，冲刷群桩基础越倾向于摇摆耗能，反之，越倾向于塑性耗能。为了方便应用，本研究建立的地震耗能机制数据集和神经网络模型已公开于 https://bit.ly/JW912。

关键词：桥梁工程；冲刷群桩基础；地震耗能机制；机器学习；变量重要性分析

中图分类号：TU473.1 文献标志码：A doi: 10.6052/j.issn.1000-4750.2024.03.0185

MACHINE LEARNING-DRIVEN EFFICIENT IDENTIFICATION AND ANALYSIS OF SEISMIC ENERGY DISSIPATION MECHANISMS FOR SCOURED BRIDGE PILE-GROUP FOUNDATIONS IN COHESIONLESS SOILS

WANG Jing-cheng ^{1,2} , YE Ai-jun ^{1,2} , WANG Xiao-wei ^{1,2} , ZHOU Lian-xu ^{3}

(1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;
2. Department of Bridge Engineering, Tongji University, Shanghai 200092, China;
3. School of Engineering, University of British Columbia, Kelowna, BC V1V 1V7, Canada)

Abstract: Scour can transfer the seismic vulnerable portions of a bridge from piers to pile-group foundations, which increases the cost and difficulty of implementing the conventional capacity-protection design strategy for pile-group foundations. Therefore, leveraging the energy dissipation of pile-group foundations becomes a potential alternative strategy. The seismic energy dissipation mechanisms of scoured bridge pile-group foundations are mainly categorized into three types, i.e., rocking-induced energy dissipation, plasticity-induced energy dissipation, and the energy dissipation induced by both the rocking and plastic behaviors. For pile-group
foundations with different soil properties, scour depths, and structural parameters, accurate and efficient identification of their seismic energy dissipation mechanisms is a premise for the seismic design of scoured bridges. However, the conventional nonlinear seismic behavior analysis of pile-group foundations relies on complex finite element simulations frequently with computational convergence problems. In this study, a machine learning-driven method is proposed for efficient identification and analysis of the seismic energy dissipation mechanism of scoured bridge pile-group foundations in cohesionless soils. A dataset for seismic energy dissipation mechanism of scoured bridge pile-group foundations is established by using the experimentally validated finite element analysis method and by random sampling technique. The optimized support vector machine, neural network, and ensemble tree algorithms are used to establish a machine learning-driven model for efficient identification and analysis of seismic energy dissipation mechanisms. The study results show that the neural network can more accurately identify the seismic energy dissipation mechanism of scoured bridge pile-group foundations with both the precision and recall basically larger than 90\% . The number of pile rows, of pile length, of pile longitudinal reinforcement ratio, of pier height and, of pile axial load ratio are important variables for the identification of the seismic energy dissipation mechanism of scoured pile-group foundations. The smaller the number of pile rows, of pile length and, of pile axial load ratio, and the larger the pile longitudinal reinforcement ratio and pier height, the more the scoured pile-group foundation tends to consume energy by the rocking behavior, and conversely, the more it tends to dissipate energy by the structural plasticity. For easy implementation, the dataset and neural network established in this study are available at https://bit.ly/JW912.

Key words: bridge engineering; scoured pile-group foundation; seismic energy dissipation mechanism; machine learning; variable importance analysis

PDF BibTeX

我国沿江、河地区路网与水网交织，目前已建成大量桥梁普遍面临河床冲刷问题1,2,3,4,5。河床冲刷会侵蚀桥梁群桩基础的承台以及桩顶周围的土体，导致群桩基础外露形成高桩承台基础。相较于粘土和粉土，砂土的抗冲刷性能更差6，砂土场地桥梁群桩基础的冲刷问题更严重。我国现行桥梁抗震设计规范7,8规定，对于采用延性抗震体系的桥梁，冲刷前完全埋置于土中的低桩承台基础应作为能力保护构件9,10，即桥墩作为延性构件屈服耗能，而群桩基础保持基本弹性以避免震后对土下桩基进行检查与修复，同时不允许桩身上拔以避免群桩基础摇摆耗能，保证结构的耗能机制单一、明确。然而，河床冲刷会降低群桩基础的侧向强度和刚度，进而显著增大群桩基础的侧向地震位移，当群桩基础的侧向强度小于桥墩的侧向强度时，桥梁的潜在塑性区会由桥墩转移至桩顶11,12,13,14,15，即冲刷后的群桩基础更容易在地震中进入塑性状态来耗散地震能量，即塑性耗能。此外，上部结构的地震惯性力以弯矩的形式作用于群桩基础，引起承台转动，而冲刷后群桩基础的转动强度和刚度会明显减小，导致承台的地震转角增大，进而在各排桩截面产生更显著的地震动轴力16，当桩顶截面的轴拉力大于其受拉承载力时，桩身上拔，群桩基础在循环地震荷载
下摇摆耗能17。而在某些情况下，冲刷桩基的侧向位移和转角均较大，群桩基础同时发生塑性耗能和摇摆耗能18。总而言之，冲刷导致桥梁的耗能位置从桥墩向基础转移，使得传统的利用桥墩耗能的能力保护设计策略难以施行，利用桩基耗能的抗震设计策略成为一种可能的替代选择。鉴于此，美国 Caltrans 规范和 AASHTO 规范允许桥梁群桩基础进行塑性和摇摆耗能，并建议开展专题研究。

目前已有不少针对群桩基础塑性耗能行为的研究。Wang 等19、Liu 等16和 Zhou 等20开展了一系列冲刷群桩基础的拟静力试验，分别研究群桩基础的塑性损伤破坏机理与延性能力、群桩效应与承台转动效应、以及塑性损伤后的残余竖向承载能力。王晓伟等21和 Zhou 等22开展群桩基础侧向地震行为的推倒 (Pushover) 分析，揭示桥梁结构、土体参数对群桩基础塑性耗能能力的影响。Zhang 等23,24设计桩基 - 单墩桥梁模型并开展拟静力试验，研究冻土场地桥梁群桩基础的非线性地震行为。最近，Wang 等25,26采用增量动力分析 (IDA) 对桥梁群桩基础的延性地震行为及性能指标进行参数分析，并结合 Pushover 分析方法和机器学习算法建立了延性性能指标数据驱动预测模型。上述研究表明，冲刷群桩基础具有可观的位移延性能力、屈后刚度
和滞回耗能能力，利用群桩基础的塑性耗能进行抗震设计是可行的。另一方面，已有学者关注到群桩基础的地震摇摆行为并进行研究。Dezi 等27在对高架桥的地震反应分析中发现了群桩基础的摇摆行为。Wang 等17开展拟静力试验和数值分析，揭示桩身上拔对群桩基础地震耗能机制的影响。研究发现，桩身上拔的摇摆群桩基础与不发生桩身上拔的群桩基础具有近似的耗能能力，但前者主要依靠轴向土 - 桩摩擦相互作用耗能，而后者主要依赖结构塑性损伤耗能。最近，Wang 等18通过开展拟静力试验研究发现群桩基础可能同时发生塑性耗能和摇摆耗能，且群桩基础发生摇摆后表现出明显的自复位特性，地震残余位移减小，同时极限延性性能减小。上述研究表明，利用群桩基础摇摆进行抗震设计同样是可行的，不同耗能机制的群桩基础具有不同的地震行为，需要采用不同的抗震设计方法。因此，建立快速、准确的群桩基础地震耗能机制识别和分析方法是利用桩基耗能进行冲刷桥梁抗震设计的关键。

然而，目前桩基础地震耗能机制的识别通常需要建立精细的、考虑土 - 桩相互作用的非线性温克尔地基梁模型，这对工程师的知识储备要求较高，同时模型的建模和分析时间长，收敛性差。另一方面，近些年机器学习技术飞速发展，已在结构工程、地震工程中广泛应用28,29。Mangalathu 和 Jeon30、Feng 等31、Liu 和 Guo32、Todorov 和 Billah33、李启明等34、冯德成与吴刚35、以及于晓辉等36利用神经网络、集成树和支持向量机等机器学习算法预测钢筋混凝土柱的失效模式、滞回本构参数、以及地震损伤状态，结果表明机器学习的预测精准度普遍优于传统的基于物理的方法；Nguyen 等37采用集成树算法对钢框架的地震损伤状态进行分类识别，准确度可达 98\% ；施文凯等38提出的支持向量机算法极其显著地提高了建筑抗震韧性指标的计算效率；王尉阔等39采用支持向量机实现 RC 框架 IDA 曲线的快速预测。机器学习模型不仅可以很好地完成分类与回归任务，同时具有可解释性，即可以通过采用 SHapley Additive exPlanations (SHAP) 方法40对模型进行解释，分析各输入变量的重要性及其对模型预测结果的影响。Mangalathu 等41、Wakjira 等42、以及 Cakiroglu 等43分别采用 SHAP 方法分析钢筋混凝土柱的失效模式、塑性较长度以及钢管混凝土柱轴向承载力预测的重要变
量，为工程设计提供了定性和定量的参考；齐婉婉等44采用 SHAP 方法分析影响地表峰值加速度的关键场地、地震动特征参数；郑志等45采用 SHAP 方法研究了地震动强度参数随地震动强度提高的解释程度演变情况；刘廷滨46等用 SHAP 方法解决锈蚀钢筋混凝土高温粘结强度预测过程中的模型可解释性问题。目前，还没有针对桥梁群桩基础地震耗能机制的设计变量重要性及影响研究，一定程度上限制了利用桩基耗能的桥梁抗震设计实践。

鉴于机器学习算法在处理分类问题方面的突出优势，本文针对砂土场地冲刷桥梁群桩基础，旨在建立机器学习驱动的地震耗能机制高效识别和分析方法。本文首先解释冲刷桥梁群桩基础的潜在地震耗能机制；随后，采用经试验验证的有限元分析方法和随机抽样方法，创建冲刷桥梁群桩基础地震耗能机制数据集；然后，建立并比较基于支持向量机、神经网络、集成树算法的地震耗能机制识别与分析方法。最后，对建立的机器学习驱动方法进行深入解释，揭示结构、土体参数对冲刷群桩基础地震耗能机制的影响机制，并确定抗震分析的重要参数。

1 地震耗能机制分类

考虑到土面以下桩身的塑性损伤难以检修，一般不在常规抗震设计的允许范围之内7，因此本文仅讨论桩身出现土面以下塑性铰之前冲刷桥梁群桩基础的地震耗能行为。根据作者以往系列研究17,18,19，冲刷桥梁群桩基础的潜在地震耗能机制可分为如下三类 (见图 1)：

  1. 摇摆耗能。群桩基础在土下桩身屈服之前桩身上拔，而桩(顶)截面保持弹性，基础主要依赖摇摆过程中桩身竖向运动引起的土-桩轴向摩擦相互作用耗能，如图1(a)所示；
  2. 塑性耗能。群桩基础在土下桩身屈服之前发生桩顶屈服，而桩身未上拔，基础主要依赖桩顶形成的塑性铰进行塑性耗能，如图1(c)所示；
  3. 摇摆-塑性共同耗能(简称“共同耗能”)。群桩基础在土下桩身屈服之前既发生桩身上拔，又发生桩顶屈服，基础同时进行摇摆耗能和塑性耗能，如图1(b)所示。

需要说明的是，本文定义的桩身上拔为当桩尖 (桩底) 的轴向抗力为 0，桩截面屈服则定义为纵向钢筋达到屈服应变。此外，共同耗能对应两种地震行
为, 即桩身上拔分别先于和后于桩顶屈服, 如图 1(b) 所示。现行的桥梁抗震设计规范7要求结构的耗能机制单一、明确, 因此共同耗能不应作为冲刷桥梁首选的耗能机制。出于此, 本文不对共同耗能的两
种地震行为进行进一步区分，对识别为共同耗能的冲刷桥梁推荐修改设计参数使其耗能机制转变为单一的摇摆耗能或塑性耗能。桥梁设计参数对耗能机制的影响将在本文的后续章节进行讨论。


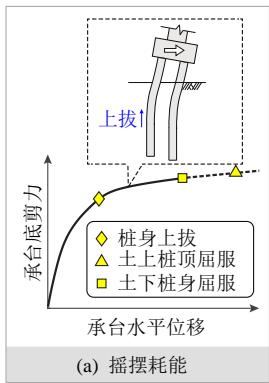
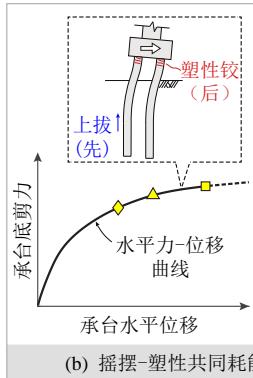
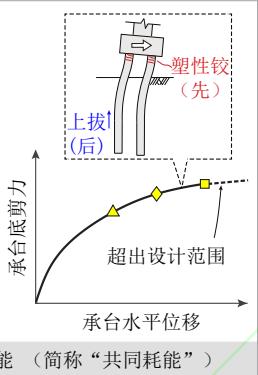
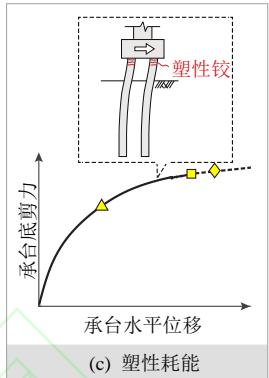
图 1 冲刷桥梁群桩基础的三类地震耗能机制
Fig.1 Three seismic energy dissipation mechanisms of scoured bridge pile-group foundations

2 地震耗能机制数据集创建

2.1 砂土场地冲刷群桩基础桥梁

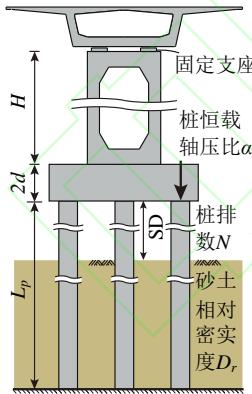
本文研究对象为砂土场地中受冲刷影响的端承式群桩基础支承的中小跨径钢筋混凝土梁式桥。本文聚焦桥梁的横桥向地震行为，一是因为横桥向往往是这类桥梁群桩基础的地震易损方向47，二是这类桥梁的各墩在横桥向具有相似的强度和刚度，可以简化为单墩模型进行研究48，如图 2(a) 所示。

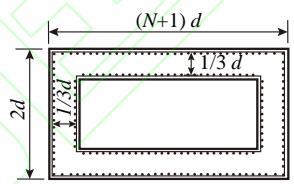
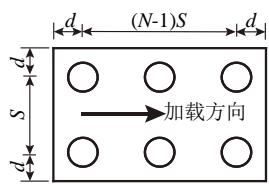
群桩基础由刚性承台和呈行列式排列的端承桩组成。需要说明的是，摩擦桩的抗拉承载能力很大，在地震中几乎不会被拔起而仅发生塑性耗能，不存在耗能机制识别问题，因此不在本文的讨论范围之内。桥梁的桥墩为矩形空心墩，上部结构为箱梁。为了聚焦群桩基础的非线性地震行为，本文不考虑支座的非线性，桥墩与主梁通过固定约束连接，这一连接方式常见于梁式桥的横桥向。


(a) 立面图


(b) 桥墩截面


(c) 承台截面


(d) 桩截面
图 2 冲刷桩基桥梁示意图


(e) 纵筋本构


(f) 混凝土本构
Fig.2 Schematic illustration of scoured bridges supported by pile-group foundations

根据先前对冲刷群桩基础地震行为和耗能机制的研究22,25, 本文共选取了 12 个桥梁结构、场地参数作为机器学习模型的输入参数, 相应的取值上下限汇总于表 1, 按实际工程统计数据和工程经验确定49,50,51,52,53,54。输入参数包括 5 个桥梁结构尺寸相关参数: 加载方向桩排数 N 、桩径 d 、桩间距 S 、桩长
L_{p} 、以及墩高 H ；4 个桥梁结构强度相关参数：钢筋屈服强度 f_{\mathrm{y}} 、保护层混凝土抗压强度 f_{\mathrm{c}} 、以及桩截面配筋率 \rho_{l} 和体积配箍率 \rho_{s} ；1 个桥梁荷载参数：桩恒载轴压比 \alpha ；以及 2 个场地土体参数：冲刷深度 SD 和砂土相对密实度 D_{r} 。桥墩和承台的尺寸与桩径和桩间距相关，见图 2(b)、图 2(c)。由于钢筋、
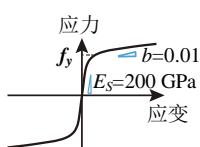
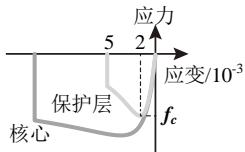
混凝土的其他材料参数对这类桥梁的地震反应敏感性较小55，本文取定值：钢筋弹性模量 200GPa，硬化率 0.01，如图 2(e) 所示；保护层混凝土的峰值

表 1 输入参数的上下限
Table 1 Upper and lower limits of input parameters

参数/单位 描述 上限 下限
N 加载方向桩排数 2 4
d/m 桩径 0.9 1.8
Lp/m 桩长 10 35
ρl/% 桩配筋率 0.5 1.5
ρs/% 桩配箍率 0.5 1.5
S/d 桩间距 2.5 3.5
fy/MPa 钢筋屈服强度 300 500
fc/MPa 保护层混凝土抗压强度 20 50
H/m 墩高 3 15
α/% 桩轴压比 5 15
SD/m 桩冲刷深度 0 6
Dr/% 砂土相对密实度 35 75

2.2 有限元模型与分析方法

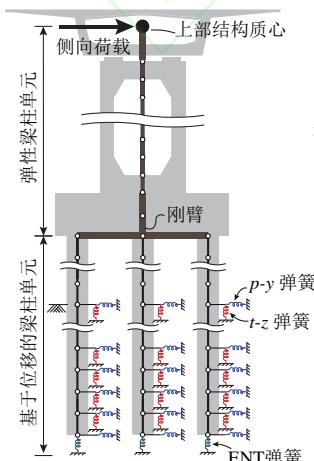
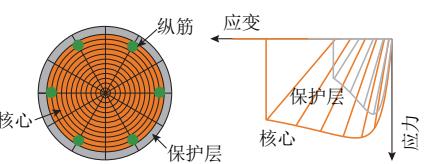
基于 OpenSees 有限元平台57，建立了冲刷桩基桥梁非线性温克尔地基梁 (BNWF) 有限元模型，如图 3 所示。桩身采用基于位移的梁柱单元模拟，每个单元 5 个积分点。桩截面采用纤维模型模拟，纤维划分如图 3(b)所示。混凝土和纵筋分别采用 Concrete04 和 Steel02 材料模拟，本构如图 3(c)、图 3(d)所示。桥墩、承台、墩 - 梁连接、以及桩 - 承台连接均采用弹性梁柱单元模拟，其中承台、墩 - 梁连接、以及桩 - 承台连接单元为刚臂，桥墩单元的刚度按实际刚度确定。

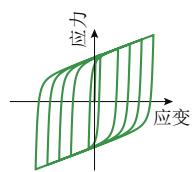
土 - 桩侧向相互作用采用 OpenSees 中的 Pysimple1 材料模拟，其本构关系如图 3(e)所示，对应美国石油协会 (API) 规范58的砂土 p - y 关系：

强度应取 0.002，极限应取 0.005，核心混凝土参数按 Mander 本构56确定，如图 2(f) 所示。

p = A \cdot p _ {u} \cdot \tanh \left(\frac {n _ {h} \cdot h}{A \cdot p _ {u}} \cdot y\right) \tag {1}

式中： p 为桩侧土抗力； y 为桩身侧向位移； A 为荷载工况系数，取 0.9； h 为埋置深度， n_h 为初始地基反应模量，是砂土的内摩擦角的函数，按 API 规范确定58； p_u 为极限桩侧土抗力，按式 (2) 确定：

p _ {u} = \min \left\{ \begin{array}{l} \left(C _ {1} \cdot h + C _ {2} \cdot d\right) \cdot \gamma \cdot h \\ C _ {3} \cdot d \cdot \gamma \cdot h \end{array} \right. \tag {2}

式中： C_1 、 C_2 、 C_3 为根据砂土内摩擦角确定的系数，按 API 规范确定58； \gamma 为砂土有效重度； d 为桩径。砂土的内摩擦角和重度根据砂土相对密实度 D_r 确定59,60。为了考虑群桩效应，对式 (2) 确定的 p_u 进行折减，即乘上一个小于 1 的 p 乘子61。由于“影子”效应22，前排桩的桩侧土抗力大于后排桩。本文参考 AASHTO 规范62，第 1、2、3、4 排桩的 p 乘子分别取 0.8、0.4、0.3、0.3。

土 - 桩轴向摩擦相互作用采用 OpenSees 中的 Tzsimple1 材料模拟，其本构关系如图 3(f) 所示，对应 Mosher63 提出的砂土 t - z 关系：

t = \frac {z}{\frac {1}{E _ {f}} + \frac {z}{t _ {u}}} \tag {3}

式中： t 为土 - 桩轴向摩擦力； z 为桩身轴向位移； E_{f} 为土 - 桩轴向摩擦力的初始模量，根据砂土内摩擦角确定63。 t_u 为极限摩阻力，根据以下式子确定63： t_u = \zeta_t\cdot K_0\cdot (\gamma \cdot h)\cdot (\pi \cdot D)\cdot \tan (0.8\cdot \varphi \cdot \pi /180) (4)


(a) BNWF 模型


(b) 桩截面纤维划分
(c) 混凝土模型


(e) p - y 弹簧模型


(f) t - z 弹簧模型


(g)ENT 弹簧模型
图 3 有限元模型
Fig.3 Finite element model

式中： k_{0} 为静止时的侧向土压力系数，取 0.4 ； \varphi 为内摩擦角； \zeta_{t} 是为了考虑侧向荷载对竖向摩擦力的提高效应64而引入的常系数，根据先前研究取 1.8^{} 。为模拟基岩提供的竖向抗力，桩尖设置弹性单压 (Elastic-No-Tension, ENT) 弹簧，受压刚度取大值 (10^{4}\mathrm{MN / m}) ，受拉刚度为 0，本构关系如图 3(g) 所示。

本文采用单向推倒 (Pushover) 分析获得群桩基础的地震行为及相应的耗能机制。如图 3(a)所示，侧向位移荷载作用于上部结构质心，模拟上部结构的地震惯性作用。考虑到研究桥梁的质量集中在上部结构，这样的荷载模式足以准确捕捉桥梁群桩基础的地震行为。侧向位移荷载的加载步长为 0.1\mathrm{mm} ，在每一个分析步中采用 Krylov-Newton 算法求解非线性静力平衡方程。需要说明的是，对于群桩基础的非线性分析，单向 Pushover 与滞回 Pushover 得到的结果几乎一致22，但单向 Pushover 的计算效率更高。在一台搭载 12th Gen Intel(R)Core(TM)i7-12700K 3.60GHz 处理器和 32.0GB RAM 的个人电脑上，完成一个工况 Pushover 分析的时间多数约 10\mathrm{min}\sim 15\mathrm{min} ，考虑到多工况可并行计算，计算效率满足建立大样本数据集的基本要求。

2.3 有限元分析方法验证

Wang 等18开展了砂土场地冲刷群桩基础 - 单墩模型的拟静力试验。在该试验中， 3\times 2 群桩基础部分埋置于均匀中密砂土，冲刷深度为 5 倍桩径；桩尖置于钢板之上，对应端承桩的边界条件；桩截面恒载轴压比为 5\% ，幅值不断增大的水平位移循环荷载作用于承台之上的刚性桥墩顶部。试验模型的土体、结构特性及加载方式均与本文接近，且试验中群桩基础既发生桩身上拔又发生桩顶屈服，试验结果可以同时验证有限元模型预测群桩基础摇摆和塑性耗能的能力。采用本文有限元分析方法得到的骨架曲线以及桩身曲率分布的结果与试验记录结果的对比分别如图 4 和图 5 所示。总体上看，有限元分析结果与试验结果吻合较好，验证了有限元分析方法预测群桩基础地震耗能机制的能力。


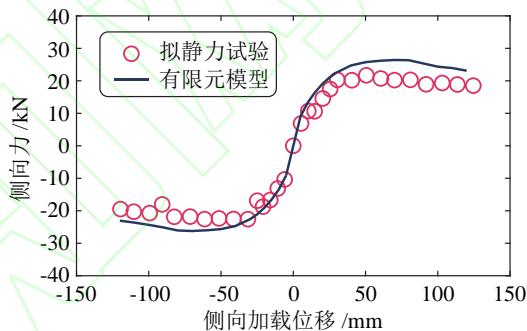
图 4 有限元模型验证：试件骨架曲线
Fig. 4 Validation of the finite element model: Skeleton curve of the specimen


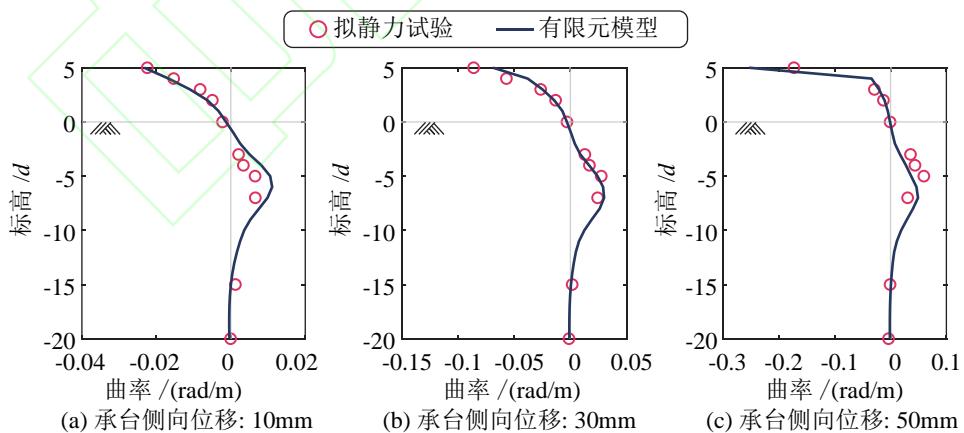
图 5 有限元模型验证：桩身曲率分布
Fig.5 Validation of the finite element model: Pile curvature distribution

2.4地震耗能机制数据集

为尽可能涵盖工程中的可能工况，且考虑机器学习数据集平衡性的要求，本文首先假定各输入变量 (参数) 服从均匀分布 (上下限如表 1 所示) 进行随
机抽样，并对抽取的参数进行随机组合，获得 500 个桥梁样本，建立有限元模型并进行 Pushover 分析。需要说明的是，相较于假定参数为正态分布，假定参数为均匀分布能更好地平衡参数上、下限范
围内的取值，即更全面地覆盖工程中可能出现的情况，保证数据集的平衡性，从而更好地揭示参数的重要性及影响。

计算结果表明，发生摇摆耗能的样本数明显小于发生塑性耗能的样本数，即样本存在类别不平衡问题，可能导致机器学习分类模型的性能显著降低26。为了解决类别不平衡问题，在 500 个样本的基础上继续抽取桩排数 N 较小、桩长 L_{p} 较短、桩配筋率 \rho_{l} 较大、墩高 H 较大、以及轴压比 \alpha 较小的样
本，以使数据集中摇摆耗能的样本比重增加。最终机器学习数据集变量分布如图 6 所示。数据集的样本总数为 1284，其中摇摆耗能、共同耗能和塑性耗能的样本各 428 个。数据集按 7：3 分为训练集和测试集，分别用于训练和测试机器学习模型。为了保证训练集与测试集中不同类别的比例相同 (即均不存在类别不平衡问题)，先对各个类别的样本按 7：3 进行随机拆分后再进一步组合成训练集和测试集。


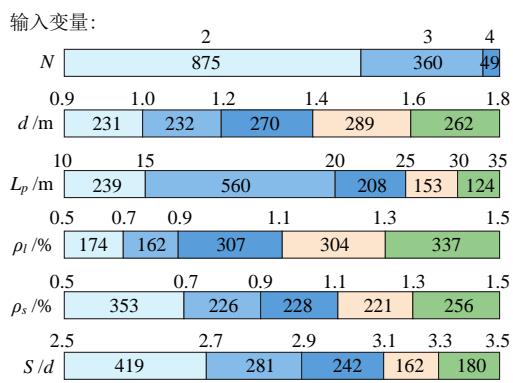
输出变量：


图 6 机器学习数据集
Fig.6 Machine learning dataset

3 机器学习驱动的地震耗能机制识别方法

3.1 机器学习算法及超参数优化

本文采用三种常用的机器学习分类算法建立冲刷群桩基础的地震耗能机制识别模型：支持向量机，神经网络，以及集成树。超参数是机器学习模型本身固有的参数，机器学习模型的训练过程就是超参数的优化过程，即搜索使得损失函数值最小的超参数取值的过程。本节将对各机器学习算法的基本原理以及超参数优化过程进行简单介绍。

支持向量机的核心思想是寻找一个超平面，使得两个类别之间的间隔最大化。这个超平面被称为最大间隔超平面，它能够实现良好的分类效果。构造最大间隔超平面涉及约束最优化问题，可以通过引入 Lagrange 函数进行求解。对于非线性问题 (即样本点不是线性可分的)，支持向量机采用核函数将数据从低维空间映射到高维空间后进行最大间隔超平面构造，实现非线性分类。常见的核函数有多项式核函数，线性核函数，以及高斯核函数等。除
了核函数，支持向量机的超参数还有框约束，核尺度参数以及多项式核函数的阶数，如表 2 所示。

神经网络是一种常见的机器学习算法，灵感来源于神经细胞间的非线性生物电传输。本文采用的浅层神经网络结构如图 7 所示。神经网络包含 1 个输入层， 1\sim N(N\leqslant 3) 个隐藏层，以及 1 个输出层。输入层的神经元个数 m 等于输入变量个数，输出层神经元个数 q 代表分类问题的类别数，每个神经元的值代表相应类别的概率。隐藏层每层包含 1~300 个神经元，神经元的值通过以下两步确定：第一步，根据前一隐藏层 (或输入层) 神经元取值及权重进行线性回归；第二步，将第一步得到的回归值输入到一个给定的激活函数中，得到的输出值即为神经元取值。激活函数的作用是在神经网络模型中引入非线性，常见的激活函数有 relu 函数，tanh 函数，sigmoid 函数等。神经网络的隐藏层尺寸、激活函数、以及正则化项强度 (为了防止出现过拟合现象而在模型的损失函数中引入的超参数，取值越大，模型的复杂度越低，越不容易出现过拟合现象) 是待优化的超参数，如表 2 所示。


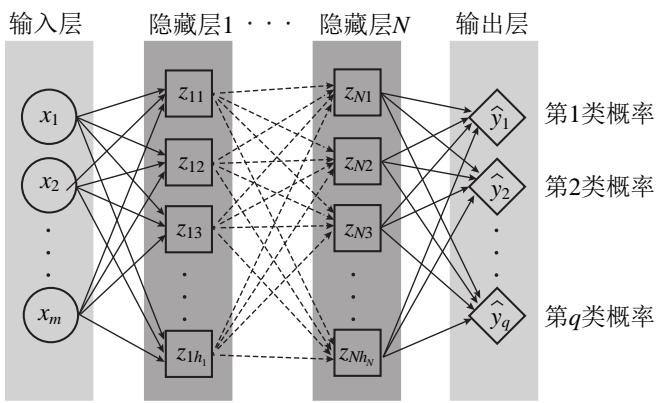
图 7 神经网络的结构
Fig.7 The architecture of neural network

集成树是一种集成机器学习算法，基本原理是通过将多个弱学习器（即决策树）采用袋袋 (Bagging)、提升(Boosting) 等方法进行集成以得到更精确、鲁棒性更好的学习器。袋袋法是先通过反复
的随机抽样训练新的弱学习器，再对所有弱学习器的预测结果取平均值的集成方法。而提升法是一种迭代算法，通过不断地使用一个弱学习器弥补前一个弱学习器的“不足”来串行地构造一个较强的学习器。除了集成方法，集成树的性能还取决于决策树个数，学习率，以及决策树的超参数 (叶节点观测的最小数量，决策拆分的最大数量以及拆分准则)，如表 2 所示。

为了权衡计算效率和精度，本文采用随机搜索确定机器学习模型的超参数，同时考虑输入变量的标准化和 5 折交叉验证。图 8 显示了随机搜索超参数的历程。各机器学习算法的损失函数最小值均随搜索次数的增加而迅速下降并趋于稳定。最终，每个算法各搜索 500 次后得到的最优超参数取值如表 2 所示。

表 2 随机搜索确定的机器学习模型最优超参数
Table 2 Optimal hyperparameters of machine learning models obtained from the random search

模型 超参数描述 搜索范围 最优取值
支持向量机 框约束 [10-3, 103] 443.9
核尺度参数 [10-3, 103] 15.5
核函数 多项式核，高斯核，线性核 高斯核
多项式核函数的阶数 -
神经网络 激活函数 relu 函数，tanh 函数，sigmoid 函数，none(无激活函数) tanh 函数
正则化项强度 [10-5, 105]/样本数量 0.0014
隐藏层尺寸 1层3层，每层1个300个神经元 单层12个神经元
集成树 集成方法 装袋，自适应提升，随机欠采样提升 自适应提升
决策树个数 461
收缩学习率 [10-3, 1] 0.35
叶节点观测的最小数量 [1, max(2, floor(样本数/2))], floor()为向下取整函数 24
决策拆分的最大数量 [1, max(2, 样本数-1)] 402
拆分准则 基尼多样性指数，最大偏差减小，或者二分准则 二分准则


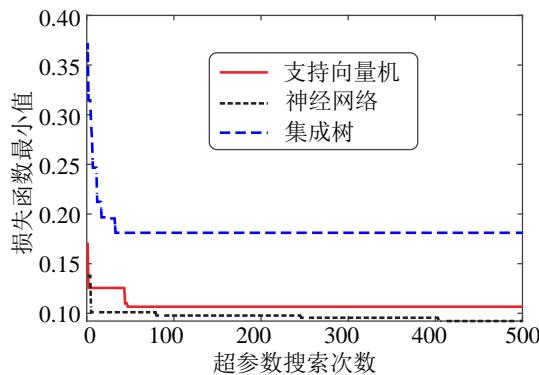
图 8 超参数优化历程
Fig.8 Hyperparameter optimization

3.2地震耗能机制分类模型验证

机器学习模型的分类性能可以由精度 (Accuracy)，查准率(Precision) 以及查全率 (Recall，又称召回率) 进行度量。精度为模型的整体性能度量，定义为被正确分类的样本数占预测样本总数的比例。每一类的识别都有相应的查准率和查全率，
其中查准率定义为正确预测为该类的样本数除以预测为该类的样本数，表征该类预测的准确率；而查全率定义为正确预测为该类的样本数除以实际观测为该类的样本数，衡量该类样本被识别的比例。精度，查准率和查全率均在 0 \sim 1(100\%) 之间，且值越大分类模型的性能越好。

图 9 显示了冲刷桥梁群桩基础地震耗能机制识别的混淆矩阵。总体上看，神经网络的表现最好，在训练集和测试集上的查准率和查全率基本都在 90\% 以上，总体精度达 94\% 。支持向量机的表现次之，查准率和查全率在 84\% 以上，总体精度达 90\% 。在三个机器学习算法中，集成树在训练集上的表现最好，达到 100\% ，即所有样本被正确预测，然而在测试集上的表现最差，查准率减小至 80\% 以下，总体精度也小于 90\% ，这表明集成树算法存在一定的过拟合现象，这可能是由超参数搜索次数过多、优化的超参数过多等因素引起的。


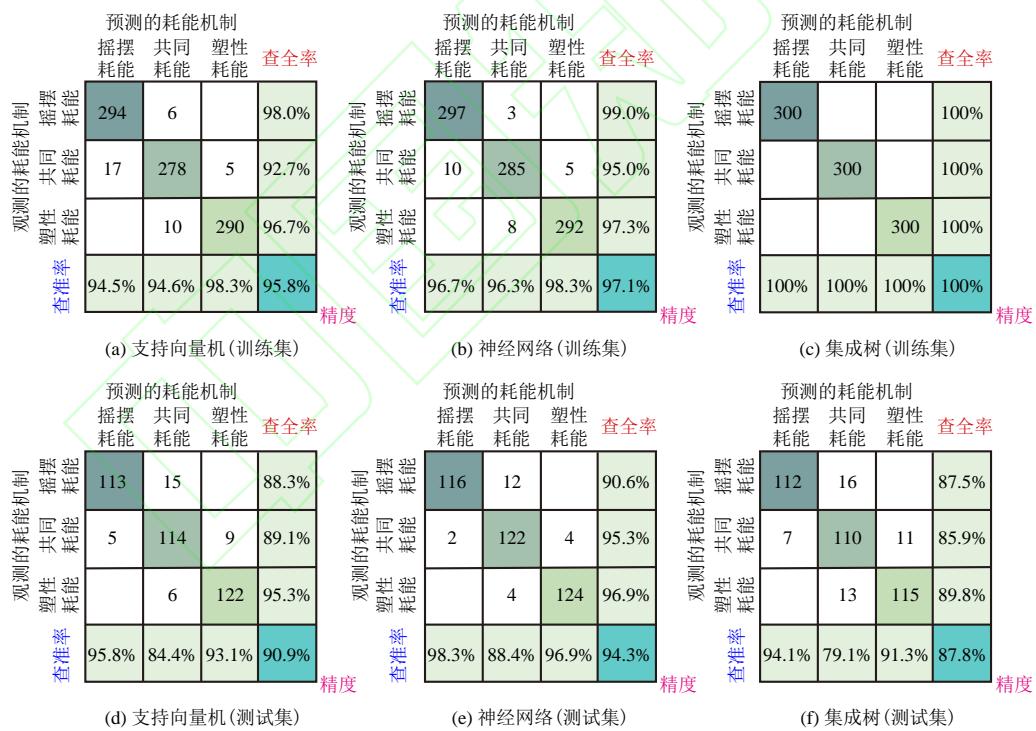
图 9 地震耗能机制识别混淆矩阵
Fig.9 Confusion matrix for the identification of energy dissipation mechanism

为了进一步对比不同机器学习算法的分类表现，图 10 绘制了冲刷桥梁群桩基础地震耗能机制识别的决策面。决策面又称决策边界，指的是机器学习分类模型预测的不同类别之间的边界。通过观察决策面的非线性程度与走向，可以分析机器学习
模型的复杂度和分类能力。计算的桥梁样本参数设置如下：桩排数 N = 2 ，桩径 d = 1.2 \mathrm{~m} ，除桩长 L_{p} ，配筋率 \rho_{l} 以及墩高 H 以外的其余参数取上下限 (见表 1) 的平均值，桩长 L_{p} ，配筋率 \rho_{l} 以及墩高 H 的取值如图 10 所示。由图可知，冲刷群桩基础地震
耗能机制的决策面呈现一定的非线性。支持向量机与神经网络模型的决策面呈现光滑连续的曲线，而集成树模型的决策面为锯齿形。图 10(i) 的结果表明，当墩高小于 8\mathrm{m} ，集成树预测的群桩基础耗能机制几乎不随桩配筋率变化，这显然不符合理论分析的结果，即提高桩配筋率会阻碍桩进入塑性，导致基础倾向于摇摆耗能，正如支持向量机和神经网络给出的预测结果 (图 10(g)、图 10(h))。同理，在图 10(c)(f) 中，集成树预测的耗能机制在较大范围内不随桩长、墩高和配筋率变化是不符合物理规律的，而支持向量机与神经网络的结果 (图 10(a)、图 10(b) 与图 10(d)、图 10(e))接近且符合定性分析规律，即桩越长，墩越矮(即群桩基础承受的弯矩越小)，配筋率越小，群桩基础越倾向于塑性耗能。因此，支持向量机和神经网络能较好地识别群桩基础的地震耗能机制，而集成树的表现欠佳。

综合考虑混淆矩阵和决策面的结果，本文推荐采用神经网络模型对群桩基础的地震耗能机制进行快速、准确地识别。为了方便应用，本文建立的
地震耗能机制数据集和神经网络模型已公开于 https://bit.ly/JW912。神经网络模型基于 MATLAB 平台运行，在用户交互界面输入桥梁的各项结构、土体参数后即可在命令行窗口查询群桩基础地震耗能机制的识别结果。

4 机器学习驱动的地震耗能机制变量重要性分析

4.1 SHapley Additive exPlanations (SHAP) 方法

为了进一步定量分析冲刷桥梁各设计变量对群桩基础地震耗能机制的影响，本文采用 SHapley Additive exPlanations (SHAP)40对上一章中建立的神经网络分类模型进行解释。SHAP 来源于博弈论，是一种复杂机器学习模型 (俗称“黑箱子”) 的解释方法。SHAP 将机器学习模型的预测结果解释为各输入变量的归因值之和：

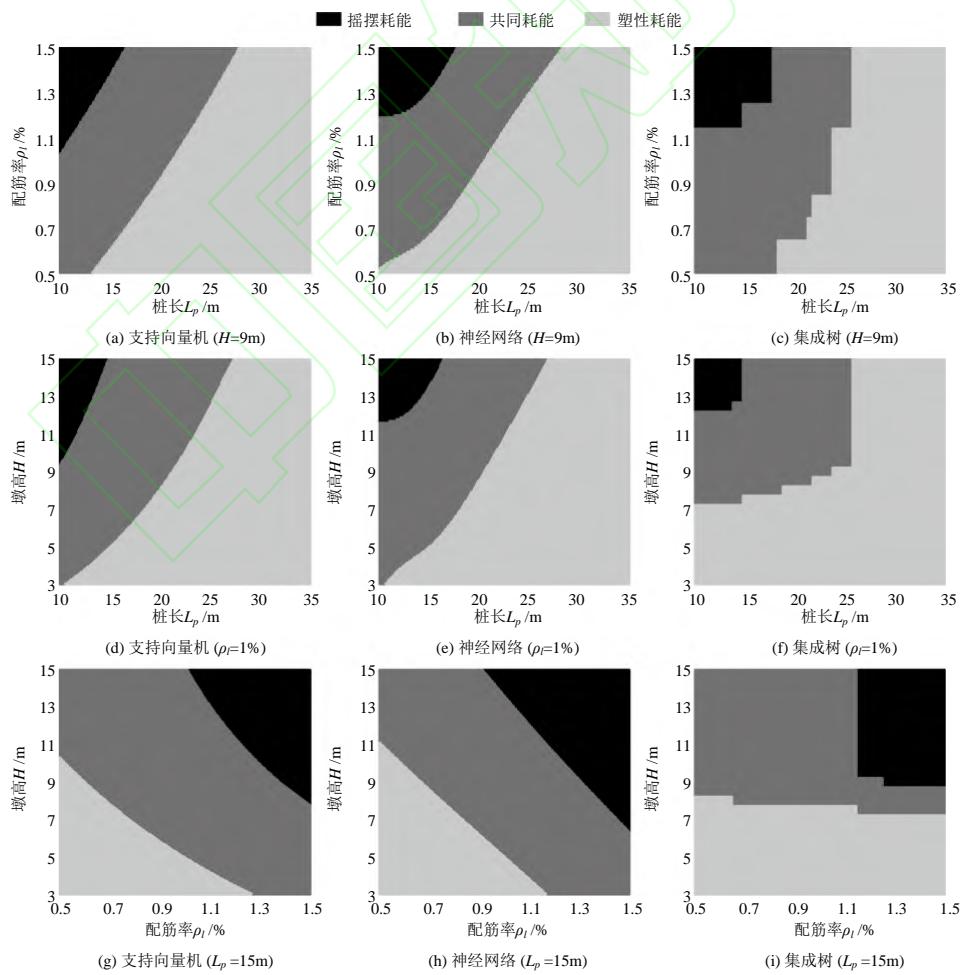
f (x) = g \left(x ^ {\prime}\right) = \phi_ {0} + \sum_ {i = 1} ^ {m} \phi_ {i} x _ {i} ^ {\prime} \tag {5}


图 10 不同机器学习方法的决策面
Fig.10 Decision surfaces for various machine learning techniques

式中： f(x) 为机器学习模型； g(x') 为 SHAP 解释模型； \phi_0 为解释模型常数； \phi_i 为第 i 个输入变量 x_i 的归因值（即 SHAP 值）； m 为输入变量总数； x_i' 根据 x_i 能否被观察到取 1 或 0。本文的涉及的问题中所有变量均能被观察， x_i' 取 1。SHAP 具有 3 个理想属性：局部准确性，缺失性和一致性。局部准确性要求各输入变量归因值之和等于机器学习模型的预测结果，即 f(x) = g(x') ；缺失性表示缺失输
入变量的归因值为零，即 x_{i}^{\prime} = 0\Rightarrow \phi_{i} = 0 ；而一致性要求变量的归因值随变量边际贡献 (即输入变量后模型预测值的变化) 的改变而改变。为了计算 SHAP 值，定义 f_{x}(S) = E[f(x)|x_{s}] ，其中 S 为输入变量的子集， f_{x}(S) 代表输入变量子集 S 的条件期望值。同时满足以上 3 个属性的 SHAP 值可按下式求解：

\phi_ {i} = \sum_ {S \subseteq \{x _ {1}, x _ {2}, \dots , x _ {M} \} \backslash \{x _ {i} \}} \frac {| S | ! (M - | S | - 1) !}{M !} \left(f _ {x} \left(S \cup \left\{x _ {i} \right\}\right) - f _ {x} (S)\right) \tag {6}

式中： \{x_{1}, x_{2}, \dots, x_{M}\} \setminus \{x_{i}\} 为在所有输入变量集合 \{x_{1}, x_{2}, \dots, x_{M}\} 中除去变量 x_{i} 后得到的集合； |S| 为子集 S 的变量个数。SHAP 方法可以局部分析每一个样本中各输入变量对预测结果的贡献，也可以通过汇总所有样本的 SHAP 结果全局分析变量的重要性及定量影响。

4.2 变量重要性分析结果讨论

输入变量的重要性可以采用整个数据集中 SHAP 绝对值的平均值 (记为 mean(|SHAP|)) 进行度量41。图 11 显示了各输入变量的重要性排序。在本文中，mean(|SHAP|) 大于 0.05 的变量被认为是重要变量，即输入该变量后地震耗能机制判定为给定类的概率变化超过 5\% ，反之，mean(|SHAP|) 小于 0.05 的变量被认为是次要变量。由图 11 可知，桩排数 N 、桩长 L_{p} 、桩配筋率 \rho_{l} 、墩高 H 以及桩轴压比 \alpha 是冲刷桥梁群桩基础地震耗能机制识别的重要变量。对于摇摆耗能和塑性耗能的识别，桩排数是最重要的输入变量，对识别概率的影响在 12\% 以上。而对共同耗能的识别，桩长是最重要的输入变
量，对识别概率的影响在 9\% 左右。此外，砂土的密实度 D_{r} 和桩的配箍率 \rho_{s} 对分类结果的影响几乎可以忽略，桩径 d 和冲刷深度 SD 也是次要变量，对所有耗能机制的识别影响都很小。桩间距 S 、纵筋屈服强度 f_{y} 和混凝土抗压强度 f_{c} 是否为重要变量取决于识别的类别，即桩间距和纵筋屈服强度为摇摆耗能识别的重要变量，而混凝土抗压强度是塑性耗能识别的重要变量。需要说明的是，冲刷深度 SD 尽管不是群桩基础地震耗能机制分类识别最重要的变量，却是影响群桩基础在地震中是否耗能的重要变量11,12,13,14,15。此外，砂土密实度 D_{r} 对地震耗能机制的影响较小，这是因为其对桩侧水平土抗力和轴向摩阻力产生的影响是同向的。例如，减小 D_{r} 会减小桩侧摩阻力，降低桩的抗拉承载能力，但同时会降低桩侧土抗力，降低了群桩基础的弯矩需求，从而减小了群桩基础桩截面的轴拉力需求，即减小 D_{r} 会同时降低桩身轴向的抗震能力与地震需求，故对耗能机制的影响相对较小。


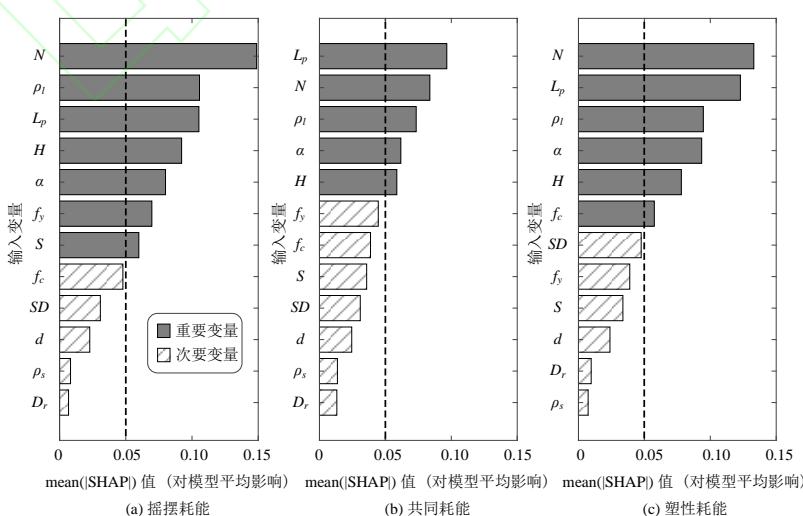
图 11 变量重要性排序
Fig.11 Variable importance ranking

图 12 汇总了整个数据集中各变量 SHAP 值的结果。图 12 中各变量从上至下按重要性 (即 mean(|SHAP|)) 递减排列，每一个点代表一个样本，点的颜色表征变量的大小(从蓝到红依次增大)，重叠点在 y 轴方向抖动， x 轴代表 SHAP 值。由图 12(a) 可知，桩排数、桩长、桩轴压比、桩间距、混凝土抗压强度、以及冲刷深度越小，桩配筋率、墩高、钢筋屈服强度、桩径以及桩配箍率越大，冲刷桥梁群桩基础发生摇摆耗能的概率越高，反之，则发生塑性耗能的概率越高，如图 12(c) 所示。对于处于摇摆耗能和塑性耗能之间的共同耗能，各变量的 SHAP 值近似均匀地分布在 0 的两侧，即各变量对冲刷桥梁群桩基础共同耗能的概率无明显的定性影响。

以数据集中被准确识别的 1# 样本为例，图 13 解释了神经网络模型识别其为摇摆耗能的原因与过程。各变量及在该样本中的取值显示在纵轴，各变量从上至下按 SHAP 绝对值递减排列，横轴为神经网络的预测结果。当所有变量都没有输入时，摇摆耗能的概率为数据集中摇摆耗能样本所占的比例，即 \phi_0 = 0.33 。随后，在神经网络模型中陆续输入 D_{r} ， f_{c},\ldots ,\rho_{l} 共 12 个变量，模型的预测值在 \phi_0 的基础上累积各变量的 SHAP 值直至达到最后的输出结果 0.951，即该工况最终有 95.1\% 的概率为摇摆耗能，远高于其他两个耗能机制的概率，因此神经网
络模型将该样本识别为摇摆耗能。此外，在该样本中变量重要性的排序与图 11(a) 的结果不一致，体现了变量局部重要性和全局平均重要性的区别。

为了进一步分析各重要变量的影响及相互之间的关联性，图 14 显示了桩排数 N 、桩长 L_{p} 、以及桩配筋率 \rho_{l} 两两之间的 SHAP 依赖图。横轴为第一个变量的取值，纵轴为第一个变量摇摆耗能的 SHAP 值，每一个点代表一个样本，点的颜色表征第二个变量的大小。为了避免横坐标相同的点发生大量重合而影响图的可读性，对各样本点的横坐标加入了一定程度的抖动。由图 14(a)、图 14(b)可知，桩排数大于等于 3 会降低群桩基础摇摆耗能的概率 (即 SHAP 值小于 0)，桩长增加会相对削弱桩排数的影响，而桩配筋率增加会进一步强化桩排数的影响。由图 14(c)、图 14(d) 可知，桩配筋率小于 1.1\% 会降低群桩基础摇摆耗能的概率，而桩排数和桩长的增加均会削弱桩配筋率的影响。由图 14(e)、图 14(f) 可知，桩长大于 20\mathrm{m} 会降低群桩基础摇摆耗能的概率，桩排数和桩配筋率分别会削弱和强化桩长的影响。

值得一提的是，基于 SHAP 分析得到的桩长 L_{p} 、桩配筋率 \rho_{l} 、墩高 H 对地震耗能机制的影响规律 (图 11~ 图 14) 与前述机器学习决策面分析 (图 10) 结果一致，且均符合物理规律，侧面印证了机器学习模型及 SHAP 分析方法的可靠性。


图 12 SHAP 汇总图
Fig.12 SHAP summary plot


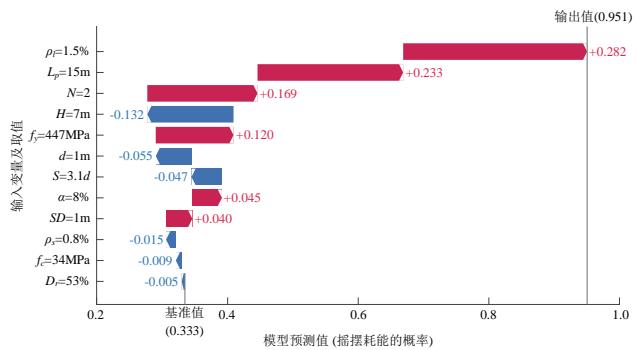
图 13 1# 工况耗能机制为摇摆耗能的解释
Fig.13 Explanation of the rocking-induced energy dissipation mechanism for Case 1#

5 结论

本文提出了一种机器学习驱动的砂土场地冲刷桥梁群桩基础地震耗能机制识别与分析方法。首先，利用有限元分析方法和随机抽样技术建立地震耗能机制数据集，再结合机器学习分类的主流算法 (支持向量机、神经网络、以及集成树) 建立地震耗能机制识别模型，并对模型进行解释，分析地震耗能机制识别的重要桥梁结构、土体参数。主要的结论如下：

(1) 本文采用的三种机器学习算法中，神经网络在识别冲刷桥梁群桩基础的地震耗能机制中表现最好，查全率和查准率基本均在 90\% 以上。支持向量机表现次之，查全率和查准率在 84\% 以上。集成树出现了过拟合现象，查准率不足 80\% ；
(2) 桩排数、桩长、桩配筋率、墩高以及桩轴压比是冲刷群桩基础地震耗能机制识别的重要变量，砂土的密实度、桩的配箍率、桩径以及冲刷深度则对冲刷群桩基础地震耗能机制的影响较小；

(3) 桩排数、桩长、桩轴压比越小，桩配筋率、墩高越大，冲刷桥梁群桩基础在地震中越倾向于摇摆耗能，反之，越倾向于塑性耗能。

需要说明的是，以上结论适用于本文参数空间内的砂土场地冲刷群桩基础支承的中小跨径钢筋混凝土梁式桥。当实际工程中桥梁结构、场地特性和参数取值不在本文的研究范围内时 (如大跨度桥梁中的大型群桩基础、特大洪水引起的极端冲刷、以及场地液化等)，本文结论仅供参考，仍需要开展进一步的专题研究。

本研究实现了冲刷桥梁群桩基础地震耗能机制的快速识别与分析。在实际工程中，桥梁设计参数变化范围大，群桩基础可能出现多种地震耗能机制，须针对不同地震耗能机制的群桩基础分别开展抗震设计，以有效控制基础的地震损伤变形。后续研究可聚焦不同地震耗能机制群桩基础的抗震性能指标，同时借助机器学习提出群桩基础地震需求的高效计算方法，与本研究成果整合形成高效的冲刷桥梁抗震设计方法。


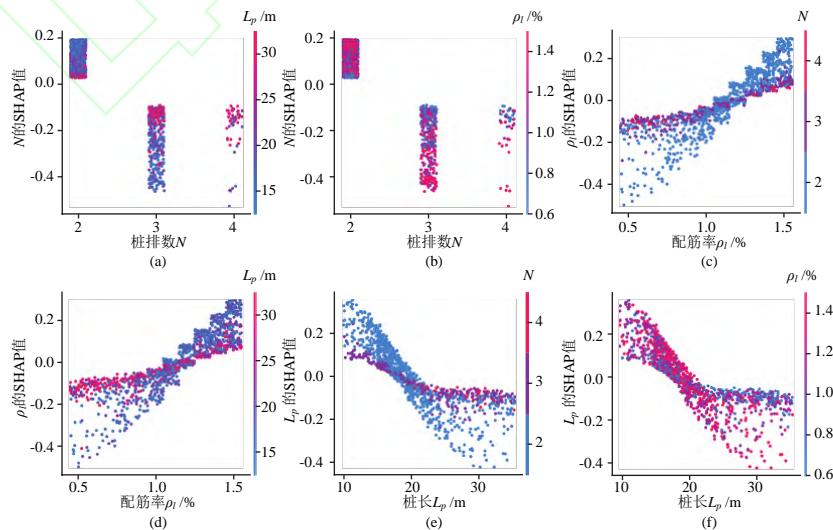
图 14 冲刷群桩基础摇摆耗能的 SHAP 依赖图
Fig.14 SHAP dependency plots for the rocking-induced energy dissipation mechanism

参考文献：

  1. WARDHANA K, HADIPRIONO F C. Analysis of recent bridge failures in the United States[J]. Journal of Performance of Constructed Facilities, 2003, 17(3): 144-150. ↩

  2. 熊文，蔡春生，张嵘钊. 桥梁水毁文献综述 [J]. 中国公路学报，2021,34(11):10-28.
    XIONG Wen, CAI C S, ZHANG Rongzhao. Review of hydraulic bridge failures[J]. China Journal of Highway and Transport, 2021,34(11):10-28. (in Chinese) ↩

  3. 周航，王增亮，刘汉龙，等. 桩基非对称局部冲刷条件下土体应力变化解析解 [J]. 中国公路学报，2021, 34(11): 72-82. ZHOU Hang, WANG Zengliang, LIU Hanlong, et al. Analytical solution of soil stress variation under condition of asymmetric local scour of pile foundation[J]. China Journal of Highway and Transport, 2021, 34(11): 72-82. (in Chinese) ↩

  4. 祝志文，刘震卿. 桥梁基础局部冲刷 CFD 模拟的研究进展 [J]. 中国公路学报, 2021, 34(11): 29-47. ZHU Zhiwen, LIU Zhenqing. Review on CFD simulations for local scour around bridge foundations[J]. China Journal of Highway and Transport, 2021, 34(11): 29-47. (in Chinese) ↩

  5. 郭健，蒋兵. 近 30 年桥梁基础冲刷研究进展及关键问题 [J]. 中国公路学报, 2020, 33(7): 1-16. GUO Jian, JIANG Bing. Research progress and key issues of bridge pile scour in recent 30 years[J]. China Journal of Highway and Transport, 2020, 33(7): 1-16. (in Chinese) ↩

  6. 王秋生，樊俊杰，王心愿，等. 堰塞体冲刷参数统计分析及快速预测方法 [J]. 工程科学与技术，2020，52(6): 83-94.
    WANG Qiusheng, FAN Junjie, WANG Xinyuan, et al. Statistical analysis and rapid prediction method of erodibility parameters of barrier dam[J]. Advanced Engineering Sciences, 2020, 52(6): 83-94. (in Chinese) ↩

  7. 中华人民共和国交通运输部. 公路桥梁抗震设计规范 (JTG/T 2231-01—2020)[M]. 北京：中华人民共和国交通运输部，2020.
    Ministry of Transport of the People's Republic of China (MTPRC). Specifications for seismic design of highway bridges(JTG/T 2231-01—2020)[M]. Beijing: MTPRC, 2020. (in Chinese) ↩ ↩ ↩

  8. 中华人民共和国住房和城乡建设部. 城市桥梁抗震设计规范 (CJJ 166-2011)[M]. 北京：中国建筑工业出版社，2011.
    Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for seismic design of urban bridges(CJJ 166-2011)[M]. Beijing: China Construction Industry Press, 2011. (in Chinese) ↩

  9. MANDER J B, DUTTA A, GOEL P. Capacity design of bridge piers and the analysis of overstrength[R]. MCEER-98-0003. Buffalo, NY: Dept. of Civil, Structural and Environmental Engineering, Univ. at Buffalo., 1998. ↩

  10. 王晓伟, 钱晋, 叶爱君, 等. 砂土场地桩柱式墩桥梁桩
    身地震需求简化计算方法 [J]. 工程力学，2023. https://doi.org/10.6052/j.issn.1000-4750.2022.10.0850 WANG Xiaowei, QIAN Jin, YE Aijun, et al. Simplified seismic demand prediction method for extended pile-shafts in cohesionless soils[J]. Engineering Mechanics, 2023. https://doi.org/10.6052/j.issn.1000-4750.2022.10.0850 (in Chinese) ↩

  11. WANG X, YE A, JI B. Fragility-based sensitivity analysis on the seismic performance of pile-group-supported bridges in liquefiable ground undergoing scour potentials[J]. Engineering Structures, 2019, 198: 109427. ↩ ↩

  12. ZHOU L, ALAM M S, WANG X, et al. Optimal intensity measure selection and probabilistic seismic demand model of pile group supported bridges in sandy soil considering variable scour effects[J]. Ocean Engineering, 2023, 285: 115365. ↩ ↩

  13. HE L G, HUNG H H, CHUANG C Y, et al. Seismic assessments for scoured bridges with pile foundations[J]. Engineering Structures, 2020, 211: 110454. ↩ ↩

  14. SONG S T, HU T F, CHIOU D J. Influence of riverbed scour on the performance of bridges subjected to lateral seismic loads[J]. Journal of Earthquake Engineering, 2020, 26(5): 2251-2282. ↩ ↩

  15. 商宇，叶爱君，王晓伟．冲刷条件下的桩基桥梁振动台试验 [J]. 中国公路学报，2017,30(12):280-289. SHANG Yu, YE Aijun, WANG Xiaowei. Shake table test of pile supported bridge under scour condition[J]. China Journal of Highway and Transport, 2017, 30(12):280-289. (in Chinese) ↩ ↩

  16. LIU T, WANG X, YE A. Roles of pile-group and cap-rotation effects on seismic failure mechanisms of partially-embedded bridge foundations: Quasi-static tests[J]. Soil Dynamics and Earthquake Engineering, 2020, 132: 106074. ↩ ↩

  17. WANG J, WANG X, LIU T, et al. Seismic uplift behavior and energy dissipation mechanism of scoured bridge pile-group foundations: Quasi-static test and numerical analysis[J]. Ocean Engineering, 2022, 266: 113172. ↩ ↩ ↩

  18. WANG J, YE A, ZHOU L. Quasi-static tests and numerical simulations of ductile seismic behavior for scoured bridge pile group foundations considering pile uplift[J]. Ocean Engineering, 2023, 290: 116370. ↩ ↩ ↩ ↩

  19. WANG X, YE A, HE Z, et al. Quasi-static cyclic testing of elevated RC pile-cap foundation for bridge structures[J]. Journal of Bridge Engineering, 2016, 21(2): 04015042. ↩ ↩

  20. ZHOU L, BARBATO M, YE A. Experimental investigation of postearthquake vertical load-carrying capacity of scoured reinforced concrete pile group bridge foundations[J]. Journal of Bridge Engineering, 2021, 26(12): 04021091. ↩

  21. 王晓伟, GUILLERMO BLANCO, 叶爱君, 等. 砂土中桥梁高桩承台基础的抗震延性能力参数分析 [J]. 土木工程学报, 2018, 51(5): 112-121.
    WANG Xiaowei, GUILLERMO BLANCO, YE Aijun, et al. Parametric study on seismic ductility capacity of bridge elevated pile-cap foundation in sand. China Civil Engineering Journal[J], 2018, 51(5): 112-121. (in Chinese) ↩

  22. ZHOU L, BARBATO M, YE A. Pile group effect modelling and parametric sensitivity analysis of scoured pile group bridge foundations in sandy soils under lateral loads[J]. Journal of Bridge Engineering, 2023, 28(8): 04023046. ↩ ↩ ↩ ↩

  23. ZHANG X, YANG Z (Joey), CHEN X, et al. Experimental study of frozen soil effect on seismic behavior of bridge pile foundations in cold regions[J]. Structures, 2021, 32: 1752-1762. ↩

  24. ZHANG X, YU S, WANG W, et al. Nonlinear seismic response of the bridge pile foundation with elevated and embedded caps in frozen soils[J]. Soil Dynamics and Earthquake Engineering, 2022, 161: 107403. ↩

  25. WANG J, WANG X, YE A. Ductile behavior of scoured RC pile-group foundations for bridges in cohesionless soils: Parametric incremental dynamic analysis[J]. Journal of Bridge Engineering, 2023, 28(9): 04023057. ↩ ↩

  26. WANG J, YE A, WANG X. Quantifying easy-to-repair displacement ductility and lateral strength of scoured bridge pile-group foundations in cohesionless soils: A classification-regression combination surrogate model[J]. Journal of Bridge Engineering, 2023, 28(11): 04023080. ↩ ↩

  27. DEZI F, CARBONARI S, LEONI G. Kinematic interaction and rocking effects on the seismic response of viaducts on pile foundations[C]//AIP Conference Proceedings: Volume 1020. Reggio Calabria: AIP, 2008: 626-633. ↩

  28. 郑史雄，雷川鹤，贾宏宇，等. 人工智能技术在桥梁抗震领域的应用综述 [J]. 地震工程与工程振动，2023,43(4). ZHENG Shixiong, LEI Chuanhe, JIA Hongyu, et al, Application overview of artificial intelligence technology in bridge seismic field[J]. Earthquake Engineering and Engineering Dynamics, 2023, 43(4). (in Chinese) ↩

  29. WANG X, MAZUMDER R K, SALARIEH B, et al. Machine learning for risk and resilience assessment in structural engineering: Progress and future trends[J]. Journal of Structural Engineering, 2022, 148(8): 03122003. ↩

  30. MANGALATHU S, JEON J S. Machine Learning-Based Failure Mode Recognition of Circular Reinforced Concrete Bridge Columns: Comparative Study[J]. Journal of Structural Engineering, 2019, 145(10): 04019104. ↩

  31. FENG D C, CETINER B, AZADI KAKAVAND M R, et al. Data-driven approach to predict the plastic hinge length of reinforced concrete columns and its Application[J]. Journal of Structural Engineering, 2021, 147(2): 04020332. ↩

  32. LIU Z, GUO A. Empirical-based support vector machine method for seismic assessment and simulation of reinforced concrete columns using historical cyclic
    tests[J]. Engineering Structures, 2021, 237: 112141. ↩

  33. TODOROV B, MUNTASIR BILLLAH A H M. Machine learning driven seismic performance limit state identification for performance-based seismic design of bridge piers[J]. Engineering Structures, 2022, 255: 113919. ↩

  34. 李启明，喻泽成，余波，等. 钢筋混凝土柱地震破坏模式判别的两阶段支持向量机方法 [J]. 工程力学，2022, 39(2):148-158. LI Qiming, YU Zecheng, YU Bo, et al. Two-stage support vector machine method for failure mode classification of reinforced concrete columns[J]. Engineering Mechanics, 2022, 39(2):148-158. (in Chinese) ↩

  35. 冯德成，吴刚. 混凝土结构基本性能的可解释机器学习建模方法 [J]. 建筑结构学报, 2022, 43(4): 228-238. FENG Decheng, WU Gang. Interpretable machine learning-based modeling approach for fundamental properties of concrete structures[J]. Journal of Building Structures, 2022, 43(4): 228-238. (in Chinese) ↩

  36. 于晓辉，王猛，宁超列. 基于机器学习的钢筋混凝土柱失效模式两阶段判别方法 [J]. 建筑结构学报，2022,43(8):220-231. YU Xiaohui, WANG Meng, NING Chaolie. A machine-learning-based two-step method for failure mode classification of reinforced concrete columns[J]. Journal of Building Structures, 2022, 43(8): 220-231. (in Chinese) ↩

  37. NGUYEN H D, LAFAVE J M, LEE Y, et al. Rapid seismic damage-state assessment of steel moment frames using machine learning [J]. Engineering Structures, 2022, 252: 113737. ↩

  38. 施文凯，周宇，王尉阔，等. 基向量引导支持向量机的 RC 框架抗震韧性评估 [J]. 建筑结构学报，2023. https://doi.org/10.14006/j.jzjgxb.2022.0922
    SHI Wenkai, ZHOU Yu, WANG Weikuo, et al. Basis vectors-guided support vector machines for seismic resilience assessment of RC frames[J]. Journal of Building Structures, 2023. https://doi.org/10.14006/j.jzjgxb.2022.0922 (in Chinese) ↩

  39. 王尉阔，施文凯，周宇，等. 低秩矩阵引导支持向量机的 RC 框架 IDA 曲线预测 [J]. 工程力学，2023. https://doi.org/10.6052/j.issn.1000-4750.2022.12.1074
    WANG Weikuo, SHI Wenkai, ZHOU Yu, et al. Low-rank matrix guided support vector machines for ida curve prediction of RC frame[J]. Engineering Mechanics, 2023. https://doi.org/10.6052/j.issn.1000-4750.2022.12.1074 (in Chinese) ↩

  40. LUNDBERG S M, LEE S I. A unified approach to interpreting model predictions[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. NY: Curran Associates Inc., 2017: 4768-4777. ↩ ↩

  41. MANGALATHU S, HWANG S H, JEON J S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations
    (SHAP) approach[J]. Engineering Structures, 2020, 219: 110927. ↩ ↩

  42. WAKJIRA T G, ALAM M S, EBEAD U. Plastic hinge length of rectangular RC columns using ensemble machine learning model[J]. Engineering Structures, 2021, 244: 112808. ↩

  43. CAKIROGLU C, ISLAM K, BEKDAS G, et al. Explainable machine learning models for predicting the axial compression capacity of concrete filled steel tubular columns[J]. Construction and Building Materials, 2022, 356: 129227. ↩

  44. 齐婉婉，孙锐，郑桐，等. 融合 XGBoost 和 SHAP 的地表峰值加速度预测分析模型 [J]. 岩土工程学报，2023, 45(9): 1934-1943.
    QI Wanwan, SUN Rui, ZHENG Tong, et al. Prediction and analysis model for ground peak acceleration based on XGBoost and SHAP[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(9): 1934-1943. (in Chinese) ↩

  45. 郑志，王勇，温卫平，等. 基于机器学习的核电厂震后损伤评估及响应预测方法 [J]. 工程力学，2023. https://doi.org/10.6052/j.issn.1000-4750.2023.04.0250
    ZHENG Zhi, WANG Yong, WENG Weiping, et al. A machine learning-based approach to post-earthquake damage assessment and response prediction for nuclear power plants. Engineering Mechanics, 2023. https://doi.org/10.6052/j.issn.1000-4750.2023.04.0250 ((in Chinese) ↩

  46. 刘廷滨，黄滔，欧嘉祥，等. 基于 ANN 和 XGB 算法的锈蚀钢筋混凝土高温粘结强度预测方法 [J]. 工程力学，2024, 41(增刊): 300-309.
    LIU Tingbin, HUANG Tao, OU Jiaxiang, et al. Prediction method of bond strength of corroded reinforced concrete at high temperature based on ANN and XGB algorithm. Engineering Mechanics, 2024, 41(Suppl): 300-309. (in Chinese) ↩

  47. HUTCHINSON T C, CHAI Y H, BOULANGER R W, et al. Inelastic seismic response of extended pile-shaft-supported bridge structures[J]. Earthquake Spectra, 2004, 20(4): 1057-1080. ↩

  48. WANG X, SHAFIEEZADEH A, YE A. Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground[J]. Bulletin of Earthquake Engineering, 2018, 16: 229-257. ↩

  49. DAS B. Principles of foundation engineering[M]. Stamford, USA: Cengage Learning, 2011. ↩

  50. BLANCO G, YE A, WANG X, et al. Parametric pushover analysis on elevated RC pile-cap foundations for bridges in cohesionless soils[J]. Journal of Bridge Engineering, 2019, 24(1): 04018104. ↩

  51. RAMANATHAN. Next generation seismic fragility curves for California bridges incorporating the evolution in seismic design philosophy[D]. Ph.D. thesis, Georgia Institute of Technology, 2012. ↩

  52. JONES A L, KRAMER S L, ARDUINO P. Estimation of uncertainty in geotechnical properties for performance-based earthquake engineering [R]. Berkeley, CA: Pacific Earthquake Engineering Research Center, 2002. ↩

  53. PEER(PACIFIC EARTHQUAKE ENGINEERING RESEARCH CENTER). Structural performance database[EB]//http://nisee.berkeley.edu/spd/index.html. (2003). ↩

  54. AVIRAM A, MACKIE K, STOJADINOVIC B. Guidelines of nonlinear analysis of bridge structures in California[R]/PEER report. Berkeley, CA: Pacific Earthquake Engineering Research Center, 2008. ↩

  55. 王晓伟，叶爱君，罗富元. 液化场地桩柱式基础桥梁结构地震反应的敏感性分析 [J]. 工程力学, 2016, 33(8): 132-140.
    WANG Xiaowei, YE Aijun, LUO Fuyuan. Sesimic response sensitivity analysis of pile supported bridge structures in liquefiable ground[J]. Engineering Mechanics, 2016, 33(8): 132-140. (in Chinese) ↩

  56. MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826. ↩

  57. MCKENNA F. OpenSees: A framework for earthquake engineering simulation[J]. Computing in Science and Engineering, 2011, 13(4): 58-66. ↩

  58. API(AMERICAN PETROLEUM INSTITUTE). Recommended practice for planning, designing and constructing fixed offshore platforms - Working stress design[M]. Washington, DC: API, 2005. ↩ ↩ ↩

  59. WANG X, LUO F, SU Z, et al. Efficient finite-element model for seismic response estimation of piles and soils in liquefied and laterally spreading ground considering shear localization[J]. International Journal of Geomechanics, 2017, 17(6): 06016039. ↩

  60. ROLLINS K M, LANE J D, GERBER T M. Measured and computed lateral response of a pile group in sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(1): 103-114. ↩

  61. BROWN D A, MORRISON C, REESE L C. Lateral load behavior of pile group in sand[J]. Journal of Geotechnical Engineering, 1988, 114(11): 1261-1276. ↩

  62. AASHTO. AASHTO LRFD bridge design specifications[M]. Washington, DC: AASHTO, 2012. ↩

  63. MOSHER R L. Load-transfer criteria for numerical analysis of axially loaded piles in sand. Part 1: Load-transfer criteria.[R]. Vicksburg, MS: US Army Engineer Waterways Experiment Station, 1984. ↩ ↩ ↩

  64. MADHUSUDAN REDDY K, AYOTHIRAMAN R. Experimental studies on behavior of single pile under combined uplift and lateral loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(7): 04015030. ↩

评论
Copyright © 2025 桥梁抗震小站 All Rights Reserved. Powered by Halo.