王靖程,叶爱君,王晓伟
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:采用严格的增量动力分析 (IDA) 方法对砂土场地桥梁群桩基础的延性性能开展了系统研究。基于砂土中单墩 - 群桩基础体系振动台试验验证了数值模拟方法;以实际工程为背景,考虑与结构、土体相关的 9 个参数,建立了一系列分析模型;将 7 条实际地震记录作为输入,进行了系统的增量动力分析。基于计算结果,对地震下桥梁群桩基础的损伤破坏过程进行了验证,提出了表征群桩基础延性性能的位移、转角、强度 3 个指标,并揭示了各性能指标随结构、土体参数的变化规律。结果表明,群桩基础在易修复状态下的平均位移延性系数为 2.52,平均水平承载力为首次屈服状态的 1.41 倍;极限状态下平均位移延性系数为 3.62,平均水平承载力为首次屈服状态的 1.47 倍,延性性能可观且稳定;承台转动引起的桥墩漂移率最大不超过 0.7\%,不控制抗震设计。
关键词:群桩基础;延性性能;增量动力分析;位移延性;水平承载力;承台转角
中图分类号:U442.5+5 文献标志码:A
Ductile Seismic Performance Analysis of Bridge Pile-group Foundations in Sand
WANG Jingcheng, YE Aijun, WANG Xiaowei
(State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: In this paper, the rigorous incremental dynamic analysis (IDA) method is employed to systematically investigate the ductile seismic performance of pile-group foundations (PGFs). A shake-table test on the pier-PGF system in sand is firstly used to validate the numerical modelling technique. Based on the engineering practice, a series of analytical models are then established considering the variation of nine structural/geotechnical parameters. Seven ground motion records are selected for the implementation of IDA. Finally, the seismic failure process of PGFs is validated and three performance indicators in terms of displacement, rotation and strength are proposed. And the impact of each parameter on the proposed performance index is investigated. It is found that for PGFs in the easy-to-repair state, the average displacement ductility is 2.52 and the average lateral strength is 1.41 times of that of the first-yield state. The average ultimate displacement ductility of PGFs is 3.62 and the average ultimate lateral strength is 1.47 times of that of the first-yield state. The maximum drift ratio of the pier induced by pile-cap rotation is less than 0.7\% .
Keywords: pile-group foundations (PGFs); ductile performance; incremental dynamic analysis (IDA); displacement ductility; lateral strength; pile-cap rotation
群桩基础是桥梁工程中广泛采用的基础形式。为了方便震后损伤的检查和修复,各国现行桥梁抗震设计规范多采用对群桩基础进行能力保护的抗震设计策略,即桥墩作为延性构件进行塑性耗能,而群桩基础作为能力保护构件保持弹性。这样的设计策略对群桩基础的水平承载力提出较高的要求,实际工程中往往需要采用较高的桩截面配筋率。然而,对于高桩承台基础或是遭受河床冲刷后的群桩基础,桩基外露导致水平承载能力降低,而且损伤部位有从桥墩向桩基转移的趋势1,因此难以进行传统的能力保护设计。此外,墙式墩或轨道交通桥梁中的桥墩截面尺寸往往较大,抗弯能力很强,对桩基采用能力保护设计是不经济的,并且难以实现。我国城市轨道交通结构抗震设计规范允许桩基出现不同等级的延性损伤,日本、美国和新西兰的桥梁抗震设计规范同样允许桩基发生有限的塑性损伤。目前这些规范中对群桩基础延性能力的规定多是基于桥墩或是桩柱式墩的试验结果,而桥梁群桩基础相较于上述结构有着更复杂的土 - 桩、桩 - 承台以及承台 - 上部结构的相互作用2,因此有必要对桥梁群桩基础的延性性能展开研究。
目前,针对桥梁群桩基础延性性能的研究主要采用 3 种简化的静力分析方法。第 1 种方法,单独研究群桩基础中的单桩,即将桩顶转动自由度约束后在桩顶进行水平静力加载。基于该方法,Song 等3理论推导了桩位移延性与截面曲率延性的关系并确定了砂土场地中桩的位移延性能力,Chiou 等4结合理论推导和数值模拟给出了砂土场地和黏土场地中桩的位移延性能力。显然,该方法忽略了承台转动,仅适用于低桩承台基础。第 2 种方法,将群桩基础从桥梁结构中分离以单独分析,在承台中心进行静力加载。基于该方法,Wang 等5、Liu 等6以及 Zhou 等7开展了一系列拟静力试验,研究群桩基础的损伤破坏机理,王晓伟等8采用 Pushover 数值方法研究了群桩基础的延性性能。然而,该方法忽略了上部结构惯性力引起的墩底弯矩和承台转动。第 3 种方法,对单墩 - 群桩基础体系进行分析,水平静力荷载作用于墩顶。基于该方法,Zhang 等9开展了拟静力试验,研究冻土场地桥梁群桩基础的非线性行为,但该方法忽略了承台的惯性力,导致相同承台位移下承台顶的弯矩偏大,即高估了承台的转动。已有研究表明6,承台的转动不仅会改变桩的曲率需求,还会产生动轴力而改变截面抗弯能力,因此会对群桩基础的延性性能产生显著影响,但上述 3 种单点加载的静力分析方法 (加载于桩顶、承台或墩顶) 均无法准确模拟承台的转动行为。相比之下,动力时程分析可以克服静力分析方法中荷载模式的局限性,最大程度地模拟桥梁群桩基础在地震下的平动、转动行为,是公认的“精确”方法,但目前尚缺少相关研究。
本文采用增量动力分析 (IDA) 10研究地震下群桩基础的延性性能。采用砂土场地单墩 - 群桩基础体系振动台试验验证数值模拟方法,以实际工程为背景,基于结构、土体参数建立一系列数值模型,并选取实际地震动输入进行系统的 IDA。基于计算结果验证了群桩基础的损伤破坏过程,然后提出了表征群桩基础延性性能的指标,最后分析了结构、土体参数的变化对群桩基础延性性能的影响,并给出了延性性能指标的统计结果。
1 数值模拟方法验证
1.1 单墩-群桩基础体系振动台试验
商宇等11开展了砂土场地冲刷条件下的单墩 - 群桩基础体系振动台试验,如图 1a 所示。桩径 d 为 0.1 m,长为 1.9 \mathrm{m},2 \times 2 布置,桩中心距为 0.3 \mathrm{m}。承台长、宽、高分别为 0.6、0.6、0.3 m。桥墩直径 D 为 0.214 \mathrm{m},高为 1 \mathrm{m}。桥墩与桩截面的纵筋配筋率为 2\%,配箍率为 0.8\%。上部结构配重 4 t,通过预制的钢板与墩顶连接。出于试验安全考虑,桩尖的钢筋骨架与带有钢套筒的预制钢板通过 2 根短钢筋焊连,并共同浇筑。试件安装时,钢板通过螺栓固定在混凝土底座上。试验的土体采用干砂,相对密实度约为 50\%,内摩擦角约为 31^{\circ},桩自由段长度 (冲刷深度) 为 0.4 \mathrm{m}。结构、土体、土箱中布置应变片、加速度计以及拉线式位移计等传感器。
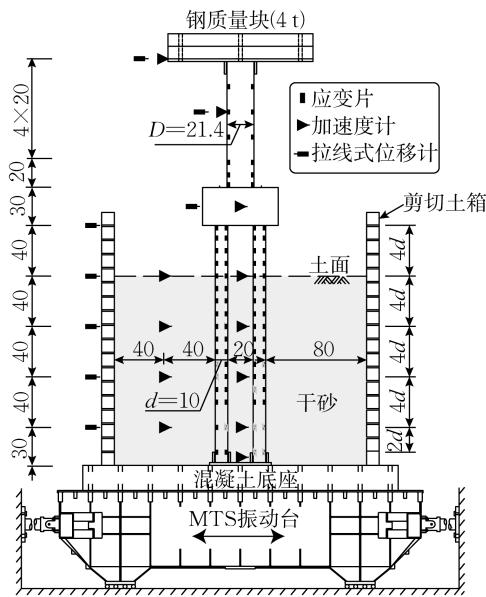
a 振动台试验
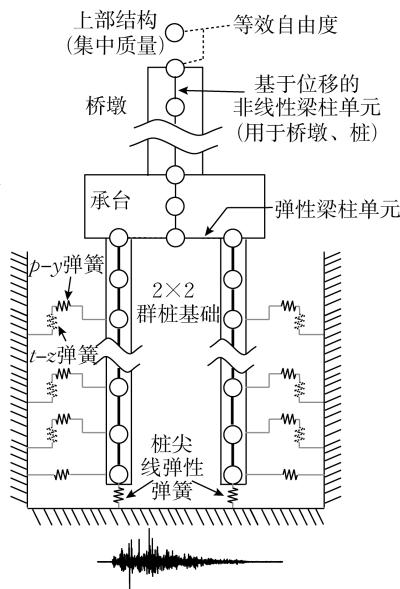
b 有限元模型
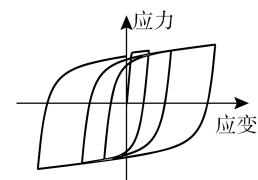
d 混凝土本构 (Concrete04 材料)
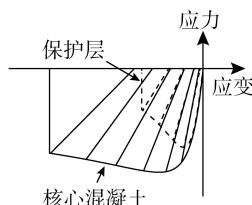
c 钢筋本构 (Steel02 材料)
图 1 振动台试验及数值模型示意图 (单位:cm)
Fig.1 Schematic diagram of shake-table test and numerical model (unit:cm)
关于试验的更多细节详见文献11。白噪声分析结果显示结构的基本周期为 0.4 \mathrm{s}。
1.2 数值模拟方法
基于 OpenSees 12平台建立的振动台试验数值模型如图 1b 所示。桥墩和桩采用基于位移的梁柱单元 (dispBeamColumn) 模拟,每个单元设置 5 个积分点,截面采用纤维单元模拟,钢筋和混凝土纤维分别采用 Steel02、Concrete04 材料模拟,本构如图 1c、d 所示。承台采用弹性梁柱单元 (elasticBeamColumn) 模拟,赋予截面大刚度以模拟刚性承台特征。上部结构节点与墩顶节点进行自由度等效。桩土侧向相互作用采用赋予 PySimple1 材料的零长单元模拟 (p-y 弹簧)。考虑土 - 桩之间的非线性接触、脱空等相互作用行为,PySimple1 材料的本构13表达式为
式中:p(y) 为土层深度 H 处桩土相对位移 y 时的桩侧土压力;A 为荷载系数(循环荷载取 0.9);k 为初始地基反力系数,是砂土内摩擦角的函数,按 ATC-32 规范14取值;p_{\mathrm{u}} 为极限土体抗力。p_{\mathrm{u}} 按下式确定13:
式中:C_{1} \sim C_{3} 为系数,是内摩擦角的函数,根据 API 规范13确定;\gamma 为土的有效重度。群桩基础在侧向荷载作用下存在群桩效应,本文采用 Mokwa15推荐的群桩效率系数对式 (2) 中的极限土体抗力 p_{\mathrm{u}} 进行折减。试验中桩中心距为 3 倍桩径,群桩效率系数取 0.8。桩侧竖向桩土相互作用采用赋予 TzSimple1 材料的零长单元 (t-z 弹簧 ) 模拟。TzSimple1 材料的本构16表达式为
式中:t(z) 为桩土竖向相对位移 \mathcal{Z} 时的桩侧摩阻力;E_{\mathrm{f}} 为桩侧摩阻力的初始模量,是内摩擦角的函数,采用 Mosher16的推荐值;t_\mathrm{u} 为桩侧极限摩阻力。t_\mathrm{u} 按下式确定17:
式中,\varphi 为以弧度为单位的内摩擦角。由于试验中桩尖的实际约束条件并非理想的固定约束,在数值模型中假设了一组线弹性弹簧,并以结构基本周期为目标,将弹簧刚度标定为 40000 \mathrm{kN} \cdot \mathrm{m}^{-1}。
1.3 数值模拟方法验证
振动台试验采用缩至 0.4g 峰值加速度的 Chi-chi 地震实测加速度记录 (见图 2a) 作为输入,该地震动输入可引起土 - 群桩基础 - 单墩体系的非线性反应。由于该地震动输入的总持时较长,为了更清晰地展现数值模拟效果,仅呈现关键持时段(对应 5\% \sim 95\% 的 Arias 强度 ) 的数值模拟与试验结果,如图 2\mathrm{b}\sim \mathrm{g} 所示。总体上看,数值模型较好地模拟了地震下桩基桥梁上部结构和承台的加速度、位移响应以及桩顶和土下桩身等关键截面的曲率响应,从而验证了数值模拟方法的可靠性。因此,下文将采用该数值模拟方法对桥梁群桩基础的延性性能进行研究。
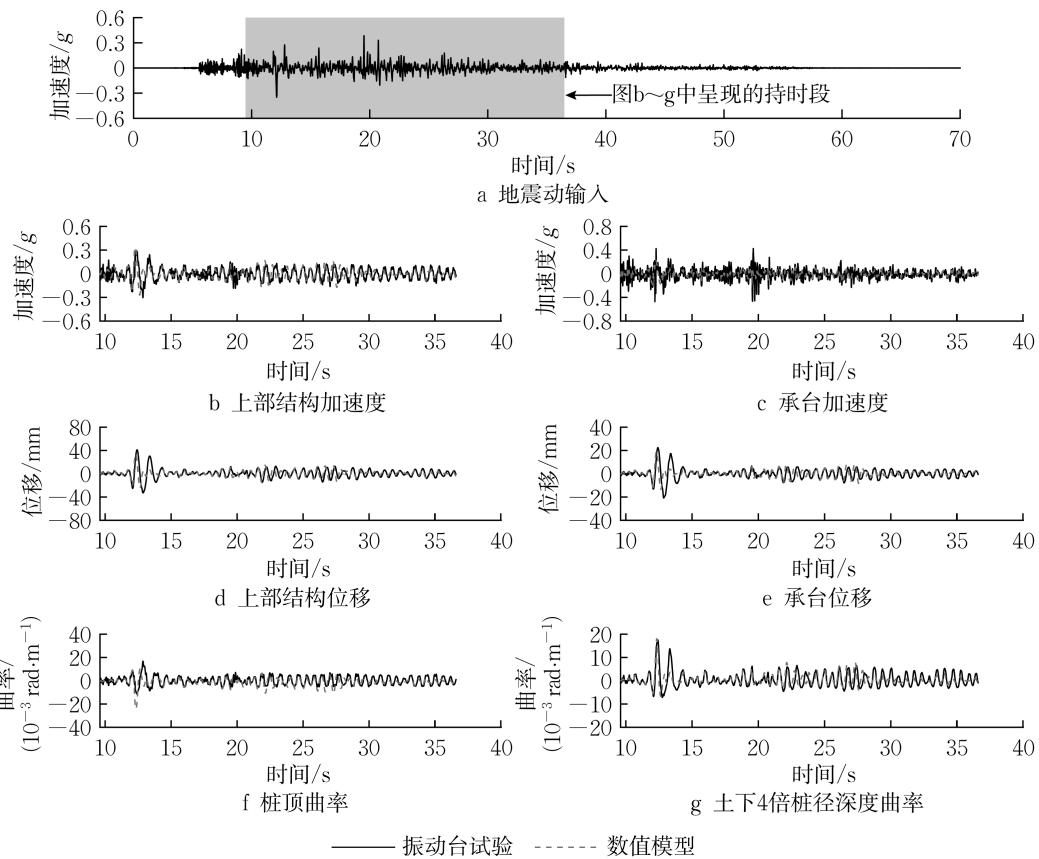
图 2 振动台试验与数值模型结构响应对比
Fig.2 Comparison of structural responses between shake-table test and numerical model
2 分析模型及IDA方法
2.1 分析模型
基于长江下游砂土场地受冲刷影响的实际桥梁工程,给出了桥梁群桩基础延性性能的分析模型,如图 3 所示。将 9 个结构、土体参数作为变量:加载方向桩排数 N、桩径 d、桩截面纵筋配筋率 \rho_{\mathrm{l}}、配箍率 \rho_{\mathrm{s}}、桩中心距 S、墩高 h、桩截面轴压比 \alpha、冲刷深度 (自由段长度) L_{\mathrm{a}}、土体相对密实度 D_{\mathrm{r}}。对于各参数,考虑大、中、小 3 个取值,每个参数的中间值形成基准工况 C0,基于基准工况 C0 每次改变 1 个参数的取值,总生成 18 个对照工况 C1~C18。需要说明的是,先前研究8已表明该工况设计方法能高效、准确地分析结构、土体参数对桩基础延性性能的影响。表 1 列出了 19 个工况 \mathrm{C0}\sim \mathrm{C18} 的参数取值。各参数取值均基于工程经验、工程调研、设计规范以及先前的学术研究,能较好地覆盖工程中的常见情况。材料参数取值如下:钢筋屈服强度 400 \mathrm{MPa},弹性模量 200 \mathrm{GPa},硬化率 0.01;素混凝土抗压强度 34 \mathrm{MPa},峰值强度对应的应变 0.002,极限应变 0.005;核心混凝土参数依据 Mander 模型18确定。承台尺寸、桥墩尺寸如图 3 所示。值得一提的是,本文关注桥梁群桩基础的延性抗震性能,因此桥墩在分析过程中假定为弹性。
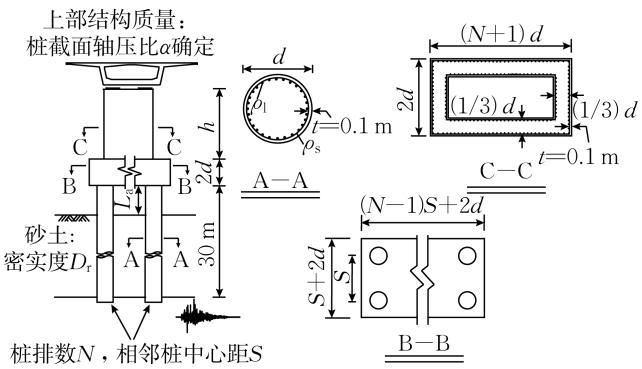
图 3 桥梁分析模型
Fig.3 Studied bridge model
表 1 工况列表
Tab.1 Case list
| 工况 | N | d/m | ρ1/% | ρs/% | S | h/m | α/% | La/m | Dr/% |
|---|---|---|---|---|---|---|---|---|---|
| C0(基准工况) | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 20 | 3 | 55 |
| C1 | 2 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 20 | 3 | 55 |
| C2 | 4 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 20 | 3 | 55 |
| C3 | 3 | 1.2 | 1.0 | 1.0 | 3.0d | 9 | 20 | 3 | 55 |
| C4 | 3 | 1.8 | 1.0 | 1.0 | 3.0d | 9 | 20 | 3 | 55 |
| C5 | 3 | 1.5 | 0.5 | 1.0 | 3.0d | 9 | 20 | 3 | 55 |
| C6 | 3 | 1.5 | 1.5 | 1.0 | 3.0d | 9 | 20 | 3 | 55 |
| C7 | 3 | 1.5 | 1.0 | 0.5 | 3.0d | 9 | 20 | 3 | 55 |
| C8 | 3 | 1.5 | 1.0 | 1.5 | 3.0d | 9 | 20 | 3 | 55 |
| C9 | 3 | 1.5 | 1.0 | 1.0 | 2.5d | 9 | 20 | 3 | 55 |
| C10 | 3 | 1.5 | 1.0 | 1.0 | 3.5d | 9 | 20 | 3 | 55 |
| C11 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 3 | 20 | 3 | 55 |
| C12 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 15 | 20 | 3 | 55 |
| C13 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 10 | 3 | 55 |
| C14 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 30 | 3 | 55 |
| C15 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 20 | 0 | 55 |
| C16 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 20 | 6 | 55 |
| C17 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 20 | 3 | 35 |
| C18 | 3 | 1.5 | 1.0 | 1.0 | 3.0d | 9 | 20 | 3 | 75 |
注:桩中心距 S 为 2.5d、3.0d 和 3.5d 时群桩效应系数分别取 0.7、0.8 以及 0.9^{}。
2.2 IDA方法
\mathrm{IDA}^{} 是将一组地震动输入调至不同强度等级后分别对结构进行动力时程反应分析以获得结构在地震下真实的损伤破坏过程及抗震性能的分析方法。本文从 PEERNGA 地震动数据库19中选取 7 条强震地震记录 ( 震级大于 5.5 级,峰值加速度大于 0.15g) 作为 IDA 的地震动输入。在 IDA 中,将每条地震动的 S_{\mathrm{a}}(T_{1})(结构基本周期对应的谱加速度值)依次调幅至 0.05g,0.10g,0.15g,…,0.35g,0.40g,0.50g,0.60g,…,直到任一桩截面达到破坏状态。截面的屈服状态对应钢筋的应变首次达到屈服应变,截面的破坏状态对应钢筋的拉应变首次达到极限(断裂)应变或核心混凝土压应变首次达到极限(压溃)应变。
3 群桩基础损伤破坏过程及性能指标
3.1 损伤破坏过程
了解结构的损伤破坏过程是研究其延性性能的基础。已往研究5通过在承台中心进行静力侧向加载的方法获得群桩基础的损伤破坏过程。结果表明:在侧向荷载作用下群桩基础的外排桩顶先屈服,随后中排桩顶、外排桩身以及中排桩身依次屈服,最后外排桩顶混凝土压溃,达到极限状态。本节以基准工况 C0 为例,基于 IDA 计算结果重新分析群桩基础的损伤破坏过程。图 4a 给出了在地震动强度 S_{\mathrm{a}}(T_{1}) 为 0.2g 时桩的曲率包络分布。由图 4a 可知,地震下群桩基础的损伤主要集中在外排桩顶、中排桩顶、外排桩身和中排桩身。图 4b 给出了这些区域钢筋应变随承台位移的发展以及损伤最严重的外排桩顶核心混凝土应变随承台位移的发展。由图 4b 可知,外排桩顶、中排桩顶、外排桩身以及中排桩身依次屈服,群桩基础的极限状态是由外排桩顶混凝土压溃导致的,此时截面的钢筋应变远小于断裂应变 (0.15)。可见,IDA 结果验证了以往研究5获得的损伤破坏过程。
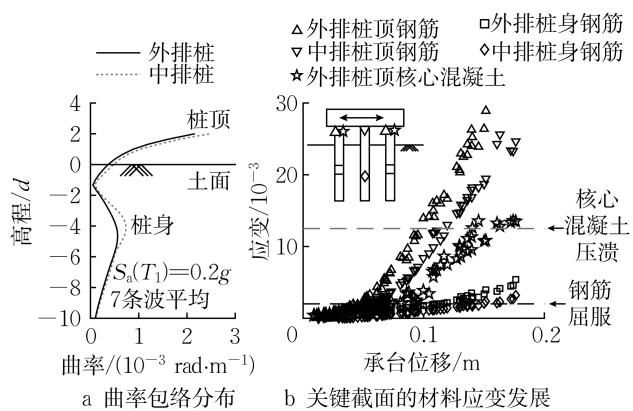
图 4 基准工况 C0 的损伤破坏过程
Fig.4 Failure process of reference case C0
3.2 性能指标
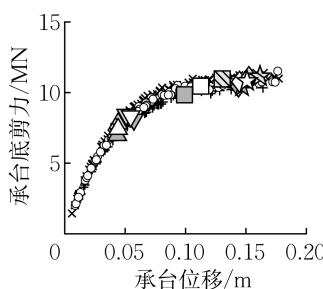
图 5 给出了基准工况 C0 下承台的力 - 位移关系、转角 - 位移关系,群桩基础在每条地震动输入下的屈服、破坏状态以及 7 条地震动输入下的平均屈服、破坏状态。由图 5 可知,群桩基础的屈服、破坏状态对地震动不敏感,因此下文中群桩基础的屈服、破坏状态取 7 条波的平均结果。

图 5 基准工况 C0 下力 - 位移关系和承台转角 - 位移关系
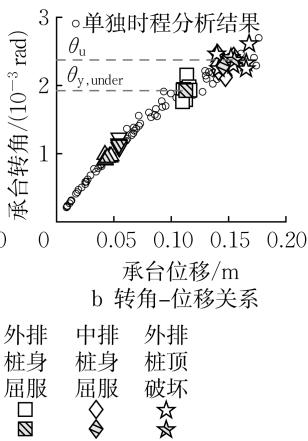
Fig.5 Force-displacement and rotation-displacement relationships of reference case C0
由图 5a 可知,当桩顶截面屈服后,群桩基础的水平承载能力仍会显著增加直至桩身截面屈服,随后水平刚度显著下降,水平承载能力小幅增加直到外排桩顶截面破坏。实际工程中,桩顶截面在土面以上或土面附近,其损伤易于检查和修复,而桩身的塑性铰在土下多倍桩径深度处(见图 4a),一旦形成将难以被发现和修复,因此应尽量避免。群桩基础在桩顶首次屈服后、桩身首次屈服前是易修复的,利用这部分延性可以获得十分可观的额外水平承载力。此外,地震动难以预测,群桩基础需要具有充足的极限变形能力,避免桩顶截面破坏造成结构的整体倒塌。基于此,本文拟采用以下指标对群桩基础在易修复状态和极限状态下的延性及强度展开研究:
式中:\mu_{\Delta, \mathrm{y}} 为易修复位移延性系数;R_{F, \mathrm{y}} 为易修复承载力提高系数;\Delta_{\mathrm{y}}, F_{\mathrm{y}} 分别为群桩基础首次屈服时承台中心的位移、承台底水平剪力;\Delta_{\mathrm{y}, \text{under}}, F_{\mathrm{y}, \text{under}} 分别为群桩基础桩身首次屈服时承台中心的位移、承台底水平剪力;\mu_{\Delta, \mathrm{u}} 为极限位移延性系数;R_{F, \mathrm{u}} 为极限承载力提高系数;\Delta_{\mathrm{u}}、F_{\mathrm{u}} 分别为群桩基础外排桩顶核心混凝土压溃时承台中心的位移、承台底水平剪力。由图 5b 可知,承台的转角与位移近似满足线性关系,随着位移的增大而增大直至达到极限状态。承台的转动会直接引起桥墩的侧向漂移,同样是抗震设计中的关键参数。因此,本文将易修复状态下的承台转角 \theta_{\mathrm{y,under}} 以及极限状态下的承台转角 \theta_{\mathrm{u}} 也作为群桩基础的性能指标进行研究。
4 群桩基础的延性性能分析
4.1 各参数对延性性能的影响
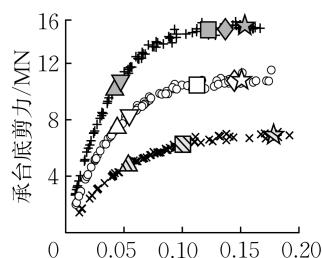
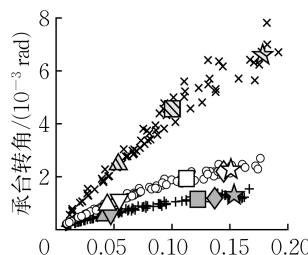
图 6 给出了桩排数 N 对群桩基础力 - 位移关系和转角 - 位移关系的影响。桩排数越多,桩顶截面的屈服、破坏位移越小,外排桩身截面的屈服位移越大,位移延性指标 \mu_{\Delta ,\mathrm{y}},\mu_{\Delta ,\mathrm{u}} 越大,各截面屈服、破坏对应的水平承载力越大,R_{F,\mathrm{y}} 从 2 排桩的 1.32 提高至 3 排桩的 1.41 后趋于稳定,R_{F,\mathrm{u}} 几乎保持不变 (1.45 \sim 1.46)。同时,桩排数越多,群桩对承台转动的限制越强,\theta_{\mathrm{y,under}},\theta_{\mathrm{u}} 越小。综合而言,桩排数越多,群桩基础的延性性能越好。
承台位移 /m
a 力 - 位移关系
承台位移 /m
b 转角 - 位移关系

图 6 桩排数对力 - 位移关系和承台转角 - 位移关系的影响
Fig.6 Impact of pile row number on force-displacement and rotation-displacement relationships
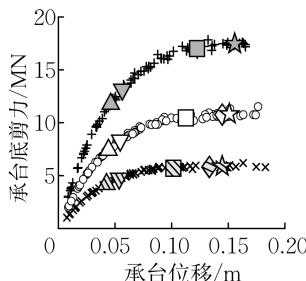
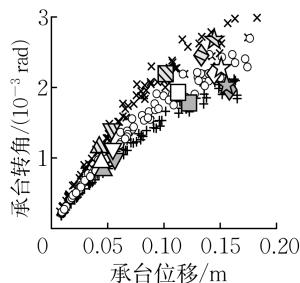
图 7 给出了桩径 d 对群桩基础力 - 位移关系和承台转角 - 位移关系的影响。桩径增大会导致桩顶截面的屈服、破坏位移小幅增大,桩身截面的屈服位移显著增大,最终导致 \mu_{\Delta ,y} 增大,\mu_{\Delta ,\mathrm{u}} 减小。同时,桩径越大,桩截面的抗弯强度越高,各截面屈服、破坏对应的水平承载力越大,R_{F,y},R_{F,u} 越大。此外,提高桩径会加强群桩对承台转动的限制,导致 \theta_{\mathrm{y,under}},\theta_{\mathrm{u}} 减小。综合而言,桩径越大,群桩基础的易修复延性性能越好。
a 力 - 位移关系
b 转角 - 位移关系

图 7 桩径对力 - 位移关系和承台转角 - 位移关系的影响
Fig.7 Impact of pile diameter on force-displacement and rotation-displacement relationships
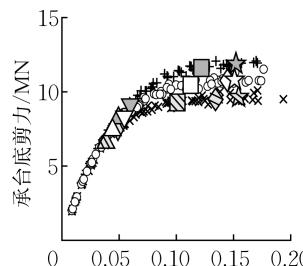
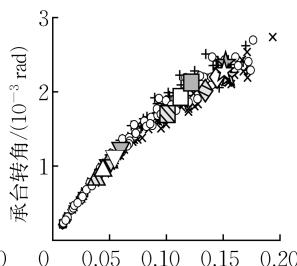
图 8 给出了桩配筋率 \rho_{\mathrm{l}} 对群桩基础力 - 位移关系和承台转角 - 位移关系的影响。配筋率越高,桩顶、桩身截面的屈服位移越大,桩顶截面的破坏位移几乎不变,\mu_{\Delta ,\mathrm{y}},\mu_{\Delta ,\mathrm{u}} 越小。同时,配筋率越高,桩截面的抗弯强度越大,各截面屈服、破坏对应的水平承载力越大,R_{F,\mathrm{y}},R_{F,\mathrm{u}} 几乎保持不变。此外,配筋率不改变承台的转动性能 (转角 - 位移关系),但是配筋率增大会导致桩身截面更晚屈服,因此 \theta_{\mathrm{y,under}} 增大,承台极限转角 \theta_{\mathrm{u}} 则与极限位移一致受配筋率的影响很小。综合而言,配筋率越小,群桩基础的延性性能越好。
承台位移 /m
a 力 - 位移关系
承台位移 /m
b 转角 - 位移关系

图 8 桩配筋率对力 - 位移关系和承台转角 - 位移关系的影响
Fig.8 Impact of pile longitudinal reinforcement ratio on force-displacement and rotation-displacement relationships
图 9 给出了桩配箍率 \rho_{s} 对群桩基础力 - 位移关系和承台转角 - 位移关系的影响。桩顶、桩身截面的屈服位移、水平承载力和转角均不随配箍率变化,因此易修复性能指标 (\mu_{\Delta ,\mathrm{y}},R_{F,\mathrm{y}},\theta_{\mathrm{y,under}}) 不随配箍率变化。然而,配箍率降低显著降低了核心混凝土的强度和极限应变18,导致桩顶截面更容易被压溃,群桩基础的极限性能指标 (\mu_{\Delta ,\mathrm{u}},R_{F,\mathrm{u}},\theta_{\mathrm{u}}) 显著下降。当配箍率过低时(如工况 C7 采用的 0.5\%),桩顶截面破坏甚至会先于外排桩身截面的屈服 (如图 9a),此时易修复性能指标与对应的极限性能指标相同,结构没有延性安全储备,这对延性抗震是非常不利的。因此,当利用群桩基础的延性进行抗震时,应保证桩顶截面具有充足的配箍率。综合而言,配箍率越大,群桩基础的延性性能越好。
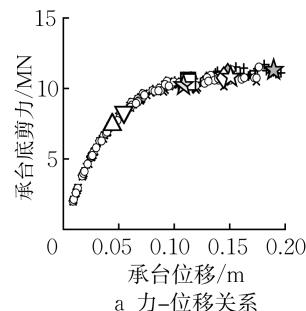
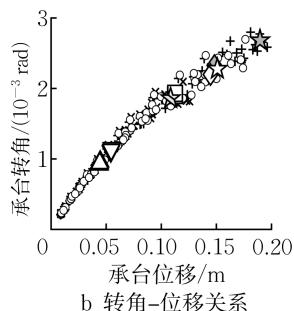

图 9 桩配箍率对力 - 位移关系和承台转角 - 位移关系的影响
Fig.9 Impact of pile transverse reinforcement ratio on force-displacement and rotation-displacement relationships
图 10 给出了桩中心距 S 对群桩基础力 - 位移关系和承台转角 - 位移关系的影响。桩中心距越大,桩顶截面屈服、破坏位移越小,外排桩身截面屈服位移越大,\mu_{\Delta, \mathrm{y}}、\mu_{\Delta, \mathrm{u}} 越大。同时,桩中心距越大,群桩效应越弱15,桩周土体抗力越大,各截面屈服、破坏对应的水平承载力越大,R_{F, \mathrm{y}} 保持不变,R_{F, \mathrm{u}} 越小。此外,桩中心距增大会限制承台的转动,导致 \theta_{\mathrm{y}, \text{under}}, \theta_{\mathrm{u}} 显著降低。综合而言,桩中心距越大,群桩基础的延性性能越好。
图 11 给出了墩高 h 对群桩基础力 - 位移关系和承台转角 - 位移关系的影响。墩高增加几乎不改变外排桩顶截面的屈服位移,但会减小桩身截面的屈服位移和桩顶截面的破坏位移,导致 \mu_{\Delta ,\mathrm{y}},\mu_{\Delta ,\mathrm{u}} 减小。同时,墩高越高,各截面屈服、破坏对应的水平承载力越小,R_{F,\mathrm{y}} 几乎不变,R_{F,\mathrm{u}} 越大。此外,墩高越高,相同承台位移下墩底 (承台顶) 弯矩越大,承台转动越显著,即 \theta_{\mathrm{y,under}},\theta_{\mathrm{u}} 越大。综合而言,墩高越小,群桩基础的延性性能越好。
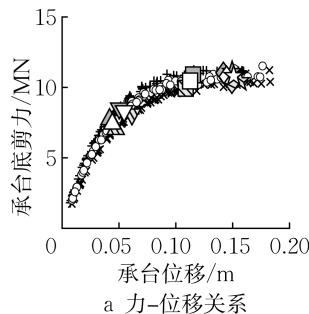
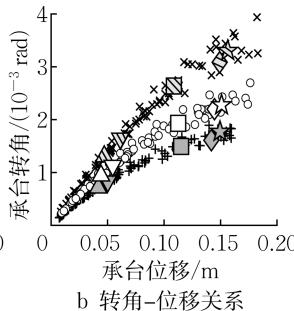
图 10 桩中心距对力 - 位移关系和承台转角 - 位移关系的影响
Fig.10 Impact of pile spacing on force-displacement and rotation-displacement relationships
a 力 - 位移关系
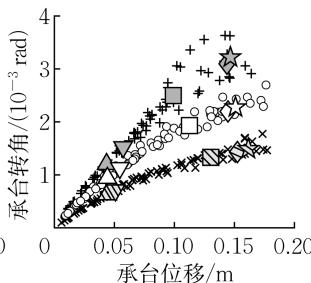
b 转角 - 位移关系

图 11 墩高对力 - 位移关系和承台转角 - 位移关系的影响
Fig.11 Impact of pier height on force-displacement and rotation-displacement relationships
图 12 给出了桩轴压比 \alpha 对群桩基础力 - 位移关系和转角 - 位移关系的影响。轴压比越大,桩截面的抗弯强度越大,群桩基础的水平承载力越高。桩轴压比对承台的转动性能基本无影响。轴压比越大,桩截面的屈服曲率 (对应钢筋受拉屈服) 越大,极限曲率 (对应核心混凝土压溃) 越小,因此各截面的屈服位移越大,桩顶截面的破坏位移越小,群桩基础极限状态的性能指标 (\mu_{\Delta ,\mathrm{u}},R_{F,\mathrm{u}},\theta_{\mathrm{u}}) 显著下降。过高的轴压比(如工况 C14 采用的 30\%)会导致桩顶截面的破坏接近于外排桩身截面的屈服(见图 12a),结构的延性安全储备很小。对于易修复状态,轴压比的增大会增大 \mu_{\Delta ,y},但会降低 R_{F,y}。
图 13 给出了冲刷深度 L_{\mathrm{a}} 对群桩基础力 - 位移关系和承台转角 - 位移关系的影响。冲刷深度越大,桩侧土提供的侧向抗力和刚度越小,导致基础的水平承载力和水平刚度越小,在相同侧向位移水平下桩截面的损伤越小,因此群桩基础的屈服、破坏对应的位移越大;同时,冲刷深度的增大会减小桩侧土对群桩基础平动的限制,使得承台更倾向于平动而非转动,导致承台转角 \theta_{\mathrm{y,under}},\theta_{\mathrm{u}} 减小。在基础各屈服、破坏状态随冲刷深度同向变化的情况下,\mu_{\Delta ,\mathrm{y}} 由冲刷深度 0\mathrm{m} 时的 2.42 增加至冲刷深度 3\mathrm{m} 时的 2.55 后保持稳定,\mu_{\Delta ,\mathrm{u}},R_{F,\mathrm{y}} 以及 R_{F,\mathrm{u}} 均随着冲刷深度的增加而降低。
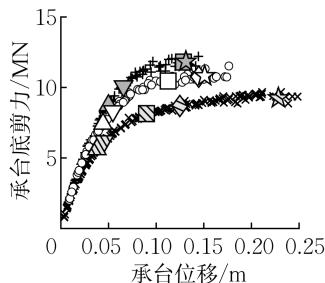
a 力 - 位移关系


b 转角 - 位移关系
图 12 桩轴压比对力 - 位移关系和承台转角 - 位移关系的影响
Fig.12 Impact of pile axial load ratio on force-displacement and rotation-displacement relationships
载力和水平刚度越小,在相同侧向位移水平下桩截面的损伤越小,因此群桩基础的屈服、破坏对应的位移越大;同时,冲刷深度的增大会减小桩侧土对群桩基础平动的限制,使得承台更倾向于平动而非转动,导致承台转角 \theta_{\mathrm{y,under}},\theta_{\mathrm{u}} 减小。在基础各屈服、破坏状态随冲刷深度同向变化的情况下,\mu_{\Delta ,\mathrm{y}} 由冲刷深度 0\mathrm{m} 时的 2.42 增加至冲刷深度 3\mathrm{m} 时的 2.55 后保持稳定,\mu_{\Delta ,\mathrm{u}},R_{F,\mathrm{y}} 以及 R_{F,\mathrm{u}} 均随着冲刷深度的增加而降低。
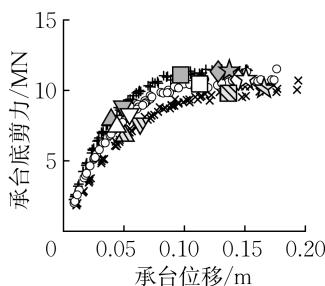
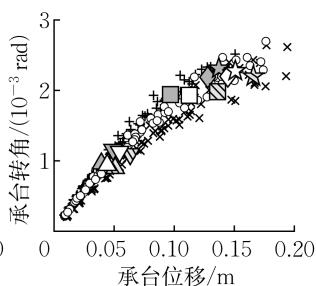
图 14 给出了土体相对密实度 D_{\mathrm{r}} 对群桩基础力 - 位移关系和承台转角 - 位移关系的影响。土体相对密实度越大,桩侧土提供的侧向抗力和刚度越大,导致基础的水平承载力和水平刚度越大,在相同侧向位移水平下桩截面的损伤越大,因此群桩基础的屈服、破坏对应的位移越小。桩顶截面的曲率需求主要由桩 - 承台之间的固定约束产生,而桩身截面的曲率需求则直接与土体抗力相关,因此相较于桩顶截面桩身截面的屈服对土体相对密实度更敏感。同时,土体相对密实度的提高增大了土体对承台平动的限制,使得承台更倾向于转动而非平动。从性能指标结果上看,\mu_{\Delta ,\mathrm{y}},R_{F,\mathrm{y}},R_{F,\mathrm{u}} 随着土体相对密实度的增大而减小,\mu_{\Delta ,\mathrm{u}} 随着土体相对密实度的增大而增大,2 个性能状态对应的承台转角 \theta_{\mathrm{y,under}},\theta_{\mathrm{u}} 则受土体相对密实度的影响较小。
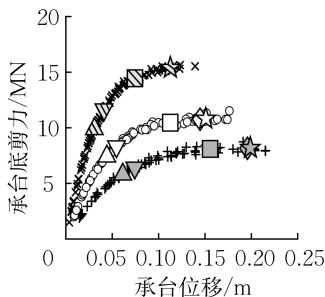
a 力 - 位移关系
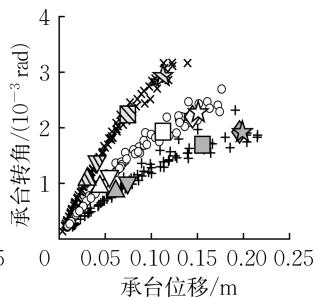
b 转角 - 位移关系

图 13 冲刷深度对力 - 位移关系和承台转角 - 位移关系的影响
Fig.13 Impact of scour depth on force-displacement and rotation-displacement relationships
a 力 - 位移关系
b 转角 - 位移关系

图 14 土体相对密实度对力 - 位移关系和承台转角 - 位移关系的影响
Fig.14 Impact of soil relative density on force-displacement and rotation-displacement relationships
4.2 延性性能指标统计
表 2 列出了所有工况中延性性能指标的统计结果。由表 2 可知,群桩基础易修复位移延性系数 \mu_{\Delta ,y} 和极限
表 2 性能指标统计
Tab.2 Statistics of performance indicators
| 工况 | μΔ,y | RF,y | θy,under/(10-3rad) | μΔ,u | RF,u | θu/(10-3rad) |
|---|---|---|---|---|---|---|
| 均值 | 2.52 | 1.41 | 2.04 | 3.62 | 1.47 | 2.63 |
| 最大值 | 2.95 | 1.46 | 4.57 | 6.17 | 1.65 | 6.77 |
| 最小值 | 1.87 | 1.32 | 1.15 | 2.45 | 1.36 | 1.32 |
| 标准差 | 0.23 | 0.03 | 0.69 | 0.72 | 0.06 | 1.13 |
| 变异系数(均值/标准差)/% | 9.3 | 2.4 | 34.0 | 19.8 | 4.4 | 43.0 |
位移延性系数 \mu_{\Delta, \mathrm{u}} 的均值分别为 2.52、3.62,变异系数分别小于 10\%、20\%,说明群桩基础的延性性能良好且相对稳定。易修复承载力提高系数 R_{F, \mathrm{y}} 和极限承载力提高系数 R_{F, \mathrm{u}} 的平均值分别为 1.41、1.47,变异系数均小于 5\%,说明群桩基础屈服后水平承载力的发展十分可观且稳定。此外,群桩基础在易修复状态下的承台转角需求 \theta_{\mathrm{y}, \text{under}} 和极限状态下的承台转角需求 \theta_{\mathrm{u}} 的最大值分别为 0.00457 rad 和 0.00677 rad,即由承台转动引起的桥墩漂移率不足 0.7\%,说明利用群桩基础的延性抗震不会在墩顶产生过量的位移需求。
5 结论
(1) IDA 结果验证了以往研究通过静力分析得到的桥梁群桩基础的地震破坏过程:外排桩顶、中排桩顶、外排桩身和中排桩身依次屈服,最终外排桩顶核心混凝土压溃,达到极限状态。当桩的配箍率过低时 ( 如 0.5\%) 或轴压比较大时 ( 如 30\%),外排桩顶截面的压溃会十分接近甚至先于外排桩身截面的屈服。
(2) 从震后易修复的角度出发,桩排数、中心距、直径、配箍率和轴压比越大,墩高、土体相对密实度、桩配筋率越小,群桩基础的延性性能越好。
(3) 桥梁群桩基础易修复、极限位移延性系数的均值分别为 2.52、3.62,变异系数分别小于 10\%、20\%,易修复、极限水平承载力提高系数的均值分别为 1.41、1.47,变异系数均不足 5\%,延性性能良好且稳定。承台转动引起的桥墩漂移率最大不超过 0.7\%,不控制抗震设计。
需要说明的是,本文结论适用于砂土场地群桩基础的延性抗震设计。后续将对黏土场地及砂土黏土多层场地的群桩基础延性抗震性能开展研究。
作者贡献声明:
王靖程:模型计算,理论分析及论文撰写与修改
叶爱君:研究选题,基金支持及论文框架指导
王晓伟:论文框架指导,论文修改。
参考文献:
SONG S T, HU T F, CHIOU D J. Influence of riverbed scour on the performance of bridges subjected to lateral seismic loads [J]. Journal of Earthquake Engineering, 2022, 26(5): 2251. ↩
XU Y, SHANG Y, YE A. Dynamic interaction between bridge pier and its large pile foundation considering earthquake and scour depths [J]. Advances in Structural Engineering, 2016, 19(9): 1390. ↩
SONG S T, WANG C Y, HU T F. Displacement ductility limits for pile foundations in cohesionless soils [J]. Journal of Earthquake Engineering, 2018, 22(4): 595. ↩
CHIOU J S, TSAI Y C. Displacement ductility capacity assessment for a fixed-head pile in cohesionless soil [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140 (1): 1. ↩
WANG X, YE A, HE Z, et al. Quasi-static cyclic testing of elevated RC pile-cap foundation for bridge structures [J]. Journal of Bridge Engineering, 2016, 21(2): 04015042. ↩ ↩ ↩
LIU T, WANG X, YE A. Roles of pile-group and cap-rotation effects on seismic failure mechanisms of partially-embedded bridge foundations: quasi-static tests [J]. Soil Dynamics and Earthquake Engineering, 2020, 132: 106074. ↩ ↩
ZHOU L, BARBATO M, YE A. Experimental investigation of postearthquake vertical load-carrying capacity of scoured reinforced concrete pile group bridge foundations [J]. Journal of Bridge Engineering, 2021, 26(12): 04021091. ↩
王晓伟, BLANCO G, 叶爱君. 砂土中桥梁高桩承台基础的抗震延性能力参数分析 [J]. 土木工程学报, 2018, 51(5): 112. WANG Xiaowei, BLANCO G, YE Aijun, et al. Parametric study on seismic ductility capacity of bridge elevated pile-cap foundation in sand [J]. China Civil Engineering Journal, 2018, 51(5): 112. ↩ ↩
ZHANG X, YU S, WANG W, et al. Nonlinear seismic response of the bridge pile foundation with elevated and embedded caps in frozen soils [J]. Soil Dynamics and Earthquake Engineering, 2022, 161: 107403. ↩
VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis [J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491. ↩
商宇,叶爱君,王晓伟. 冲刷条件下的桩基桥梁振动台试验 [J]. 中国公路学报,2017,30(12):280. SHANG Yu, YE Aijun, WANG Xiaowei. Shake table test of pile-supported bridge under scour condition [J]. China Journal of Highway and Transport, 2017, 30(12): 280. ↩ ↩
MCKENNA F. OpenSees: a framework for earthquake engineering simulation [J]. Computing in Science and Engineering, 2011, 13(4): 58. ↩
API. Recommended practice for planning, designing and constructing fixed offshore platforms : working stress design [M]. Washington DC: Americn Petroleum Institute, 2005. ↩ ↩ ↩
ATC (Applied Technology Council). Improved seismic design criteria for California bridges, provisional recommendations: ATC-32[S]. Redwood City: ATC, 1996. ↩
MOKWA R L. Investigation of the resistance of pile caps to lateral loading [D]. Blacksburg: Virginia Polytechnic Institute and State University, 1999. ↩ ↩
MOSHER R L. Load-transfer criteria for numerical analysis of axially loaded piles in sand. Part 1: load-transfer criteria [R]. Vicksburg: US Army Engineer Waterways Experiment Station, 1984. ↩ ↩
KULHAWY F H. Foundation engineering handbook [M]. Boston: Springer, 1991. ↩
MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete [J]. Journal of Structural Engineering, 1988, 114(8): 1804. ↩ ↩
POWER M, CHIOU B, ABRAHAMSON N, et al. An overview of the NGA project [J]. Earthquake Spectra, 2008, 24(1): 3. ↩