王孟欣 王靖程 叶爱君
(同济大学土木工程防灾减灾全国重点实验室,上海 200092)
摘要
基于 OpenSees 开源平台,采用基于位移的纤维梁柱单元和零长度单元,建立了考虑钢筋混凝土墩柱塑性弯曲变形和粘结滑移效应的滞回推覆(Pushover)分析有限元模型,分析了塑性铰区单元长度对墩柱弹塑性性能数值模拟结果的影响,探讨了单元长度的合理取值,最后,基于美国 \text{PEER} 结构试验数据库中 3 个弯曲破坏的钢筋混凝土悬臂墩的拟静力试验结果,验证了数值模型的正确性。结果表明:采用基于位移的梁柱单元模拟钢筋混凝土墩柱弹塑性性能时,塑性铰区单元长度对其最大水平抗力和位移延性都有显著的影响;合理单元长度为等效塑性铰长度,而等效塑性铰长度可以采用 Priestley 等17提出的经验公式计算。
关键词
钢筋混凝土墩柱,弹塑性性能,基于位移的梁柱单元,塑性铰区单元长度,等效塑性铰长度
\text{DOI}: 10.15935/j.cnki.jggs.c.20240514.001
Fiber Beam-Column Element-Based Numerical Model for Elastoplastic Performance Analysis of Column
WANG Mengxin WANG Jingcheng YE Aijun*
(State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract
Based on the OpenSees platform, a finite element model consisting of displacement-based beam-column elements (\text{DBE}) and zero-length elements is developed for cyclic pushover analysis of columns, considering the plastic flexural deformation and bond-slip effect. The influence of the element length for the plastic region on the elastoplastic performance of columns is analyzed, and the reasonable element length is discussed. Finally, the numerical model is validated based on the quasi-static tests of three reinforced concrete cantilever columns with flexural failures in the \text{PEER} structural test database. The results show that the length of the displacement-based beam-column element in the plastic region has significant effects on the horizontal strength and displacement ductility of the column. The reasonable element length should be equal to the equivalent plastic hinge length, which can be calculated using the empirical formula proposed by Priestley et al.
Keywords
reinforced concrete column, elastoplastic performance, displacement-based beam-column element, element length for plastic region, equivalent plastic hinge length
0 引言
地震荷载作用下,钢筋混凝土桥墩是最易破坏的桥梁构件之一,其地震安全性直接影响到整座桥梁的抗震性能1。随着有限元技术的不断发展,数值模拟研究也成为了桥梁结构抗震性能分析的重要方法。在钢筋混凝土墩柱抗震性能的数值模拟研究中,如何建立精度可靠的数值分析模型来客观地模拟其在滞回荷载作用下的真实弹塑性性能是核心内容。
相较于实体有限元模型,纤维梁柱单元模型具有建模简便、精度可靠和计算高效等优点2,备受国内外研究人员的青睐。目前常用的纤维梁柱单元模型主要分为两类:集中塑性模型和分布塑性模型,后者又分为基于位移法和力法的分布塑性模型3,4。分布塑性模型通过纤维截面和非线性材料本构实现,能在构件任意位置形成塑性铰5,广泛应用于结构抗震分析领域。采用分布塑性纤维梁柱模型进行非线性分析时,单元长度的划分至关重要6,决定着其是否能够客观地反映结构的真实非线性响应。
\text{OpenSees} (\text{Open System for Earthquake Engineering Simulation}) 开源地震模拟平台具备丰富的材料本构模型、单元模型和强大的非线性有限元求解功能, 适用于钢筋混凝土墩柱在地震荷载作用下的非线性分析。\text{OpenSees} 开源平台提供的基于力的梁柱单元 (\text{Force-Based Beam-Column Element, FBE}) 和基于位移的梁柱单元 (\text{Displacement-Based Beam-Column Element, DBE}) 分别对应基于力法和位移法的分布塑性纤维梁柱单元模型。相较于 \text{FBE} 模型, \text{DBE} 模型的弹塑性性能主要与材料非线性和单元长度划分有关, 而不受积分点数量的控制7, 其计算过程简单高效, 且在非线性分析中具备更好的收敛性8, 因此, \text{DBE} 模型在结构抗震分析中的应用更为广泛。但在既往研究中, \text{DBE} 模型的建模细节较为模糊, 尤其是在单元长度划分方面, 仅有少量文献讨论了 \text{DBE} 模型的合理单元长度划分方法。\text{Coleman} 和 \text{Spacone}9 结合理论分析和数值模拟结果指出: 对于截面弯矩 - 曲率响应具有软化段 (下降段) 的纤维梁柱单元数值分析模型, 塑性变形将集中于最先进入塑性状态的单元内, 其余单元在这些单元进入塑性状态后陆续发生卸载, 并始终处于弹性变形阶段, 以满足结构的整体平衡条件。对于 \text{DBE} 模型, 需要在塑性铰区单独指定一个单元, 但并未有文献说明该单元的合理长度应该如何确定; \text{Terzic}7 分别采用 \text{FBE} 和 \text{DBE} 两种类型的单元对 1 个圆形截面钢筋混凝土悬臂墩拟静力试验进行了数值模拟, 根据模拟结果指出: 对于 \text{DBE} 模型, 仅通过增加单元数量便可以提高数值模拟的精确度; 赵泰儀等10 分别采用 \text{FBE} 和 \text{DBE} 两种类型的单元对 4 个圆形截面悬臂墩和 1 个圆形截面双柱墩的拟静力试验进行了数值模拟,根据模拟结果指出:在采用 \text{DBE} 建模时,需要在塑性铰区单独设置单元,单元长度取 1.0 倍截面直径。\text{Terzic}7和赵泰儀等10所提出的建模方法均缺乏理论分析,且研究对象均局限于圆形截面墩柱,对于其他类型截面墩柱的适用性有待考量。目前,对于 \text{DBE} 模型中塑性铰区单元长度的合理取值仍没有定论。
本文基于 \text{OpenSees} 开源平台,采用 \text{DBE} 和零长度单元建立考虑钢筋混凝土墩柱塑性弯曲变形和粘结滑移效应的滞回推覆(\text{Pushover})分析有限元模型,通过改变模型中塑性铰区 \text{DBE} 的长度,分析塑性铰区单元长度对墩柱弹塑性性能数值模拟结果的影响,并探讨 \text{DBE} 模型中塑性铰区单元的合理长度取值方法。最后,以美国 \text{PEER} 结构试验数据库中 3 个不同截面形式的弯曲破坏模式钢筋混凝土墩柱拟静力试验结果为依据,验证本文建立的数值模型的正确性。
1 OpenSees有限元模型
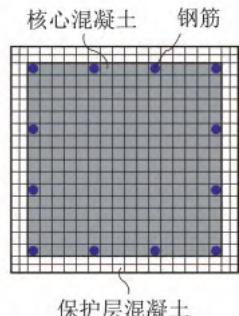
以美国 \text{PEER} 结构试验数据库中 1 个呈弯曲破坏模式的矩形截面悬臂墩 \text{Park and Paulay} 1990\text{, No.9}(以下简称 \text{PA-9})的拟静力试验为对象,建立相应的滞回推覆(\text{Pushover})分析 \text{OpenSees} 有限元模型(图 1)。墩柱 \text{PA-9} 的几何尺寸和加载方式(轴压比 10\%)详见图 1(a) 和图 1(b)。钢筋混凝土墩柱采用基于位移的纤维梁柱单元 \text{DBE} 模型,并通过 \text{PDelta Transformation} 坐标转换考虑由轴力引起的 P-\Delta 效应。墩柱纤维截面划分为纵向钢筋、核心混凝土和保护层混凝土纤维,如图 1(c) 所示。其中,核心混凝土和保护层混凝土均采用单轴材料 \text{Concrete}04 模拟,不考虑混凝土受拉,该材料对应于 \text{Mander} 模型11,其本构如图 1(d) 所示;纵筋采用单轴材料 \text{Steel}02 模拟,该材料对应具有各向同性硬化的 \text{Giuffre-Menegotto-Pinto} 模型12,其本构如图 1(e) 所示。零长度转动弹簧本构如图 1(f) 所示。纤维截面各材料的参数详见表 1。值得一提的是,箍筋不直接参与截面抗弯,因此无须进行模拟,其对截面抗弯的贡献已体现在核心混凝土的本构参数上,即相较保护层混凝土有着更高的强度和延性。
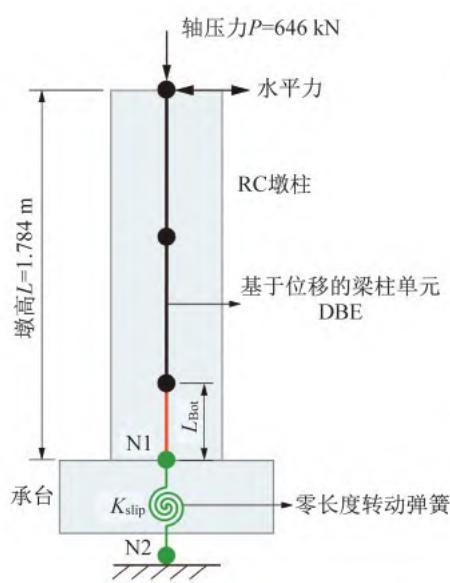
(a) 基于位移的纤维截面梁柱单元模型
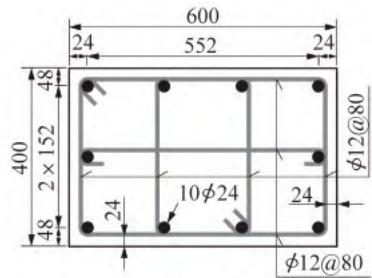
(b) 截面构造(尺寸单位:\text{mm})
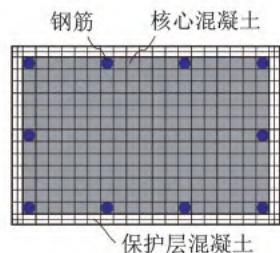
(c) 纤维截面划分
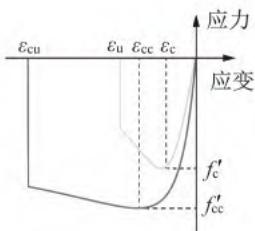
(d) \text{Concrete}04 本构
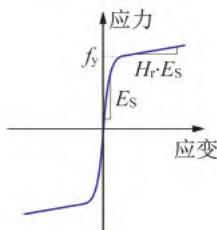
(e) \text{Steel}02 本构
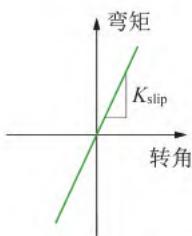
(f) 零长度转动弹簧本构
图 1 钢筋混凝土墩柱 \text{PA-9} 有限元模型
表 1 墩柱 \text{PA-9} 纤维截面材料参数
| 构件编号 | 保护层混凝土 \text{Concrete}04 | 核心混凝土 \text{Concrete}04 | 纵向钢筋 \text{Steel}02 |
|---|---|---|---|
| 抗压强度f_c'/\text{MPa} | 峰值应变\varepsilon_c | 极限应变\varepsilon_u | |
| \text{PA-9} | 26.9 | 0.002 | 0.005 |
基于 \text{Coleman} 和 \text{Spacone}9提出的观点,即塑性变形集中于最先进入塑性状态的单元内,其余单元始终处于弹性变形阶段,因此,单元长度划分方面,在图 1(a) 所示的 \text{DBE} 模型墩底处单独指定一个长度为 L_{\text{Bot}} 的 \text{DBE},其余部分均分划分为 2 个单元,各单元均设置 5 个积分点。
至于边界条件的模拟,若采用墩底固接的形式,则会忽略试验中墩柱塑性区域和承台内纵向钢筋的粘结滑移效应,从而会高估墩柱的侧向刚度、累计滞回耗能及残余位移13,无法客观反映墩柱在滞回荷载下的真实力学行为。因此,在建模中必须考虑粘结滑移效应。对于粘结滑移效应的模拟,在 \text{DBE} 模型中,可采用零长度单元法14(零长度转动弹簧法)、零长度截面单元法15(通过 \text{OpenSees} 开源平台中的 \text{zeroLengthSection Element} 和 \text{Bond\_SP}01 钢筋滑移本构实现)及等效钢筋本构法16。其中 \text{Elwood} 和 \text{Eberhard}14提出的零长度单元法相较于其他两种方法,原理简单易懂、建模高效且精度可靠,因此本文采用该方法模拟墩柱的粘结滑移效应。
以悬臂墩为例,零长度单元法的基本原理为:在墩柱底部设置一个线性本构的零长度转动弹簧 [图 1(a)],其本构如图 1(f) 所示,在一定程度上释放其转动自由度,来模拟墩柱塑性区域和承台内纵向钢筋的粘结滑移效应。零长度转动弹簧的刚度 K_{\text{slip}} 按照 \text{Elwood} 和 \text{Eberhard}14提出的经验公式计算,计算公式如下:
式中:d_s 为纵向钢筋直径;f_y 为纵向钢筋抗拉强度标准值;u 为钢筋和混凝土之间的粘结应力,其取值范围为 (0.5\sim 1.0)\sqrt{f_c'},f_c' 为混凝土圆柱体抗压强度;M_y 为截面等效屈服弯矩;\phi_y 为截面等效屈服曲率。其中截面等效屈服弯矩 M_y 和等效屈服曲率 \phi_y 根据截面弯矩曲率分析计算得到(等效双线性原则1)。
在 \text{OpenSees} 开源平台中,可以借助零长度单元 (\text{zeroLength Element}) 和线弹性单轴材料本构 (\text{Elastic Uniaxial Material})建立零长度转动弹簧。在图 1(a) 所示的 \text{DBE} 模型中,节点 \text{N}1 和 \text{N}2 坐标相同, 通过零长度单元进行连接, 该单元采用线弹性单轴材料本构, 其刚度 K_{\text{slip}} 根据式 (1) 计算。对于节点 \text{N}2, 约束其所有方向的平动和转动自由度; 对于节点 \text{N}1, 仅释放水平力作用平面内的转动自由度。
2 塑性铰区合理单元长度分析
2.1 塑性铰区单元长度对墩柱弹塑性性能的影响
为了研究 \text{DBE} 模型中塑性铰区单元长度对其弹塑性性能的影响,基于图 1(a) 所示的 \text{DBE} 模型,分别取墩底塑性铰区单元长度 L_{\text{Bot}} = 0.50H、0.75H、1.00H、1.25H 和 1.50H,H 为截面高度,以位移控制加载进行滞回 \text{Pushover} 分析。
在钢筋混凝土墩柱 \text{Pushover} 分析过程中,极限状态确定准则为:满足核心混凝土压溃或纵向钢筋拉断或水平力下降至最大水平抗力的 85\% 三个条件之一,即达到极限状态。上述 5 个墩柱 \text{DBE} 模型的极限状态均为核心混凝土压溃。在墩柱的极限状态内,提取滞回曲线的位移极值点,绘制不同模型的骨架曲线,如图 2 所示。在图 2 的基础上,根据等效双线性原则(等面积法)1和极限位移(极限状态对应的位移)计算各模型的等效屈服位移,并进一步计算各模型的位移延性系数(极限位移除以等效屈服位移),将各模型的最大水平抗力和位移延性系数计算结果汇总于表 2。
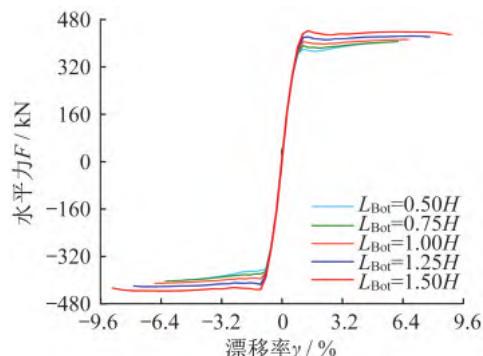
图 2 各模型骨架曲线
表 2 各模型最大水平抗力和位移延性系数
| 单元长度 L_{\text{Bot}} | 最大水平抗力 F_{\max}/\text{kN} | 位移延性系数 \mu_{\Delta} |
|---|---|---|
| 0.50H | 398.46 | 4.32 |
| 0.75H | 403.50 | 5.47 |
| 1.00H | 410.78 | 6.36 |
| 1.25H | 422.10 | 7.10 |
| 1.50H | 432.80 | 7.78 |
由图 2 可以发现,当钢筋混凝土墩柱处于弹性阶段时,基本不受 \text{DBE} 单元长度划分的影响。但随着结构进入塑性阶段,墩底塑性铰区单元长度 L_{\text{Bot}} 对墩柱的最大水平抗力(骨架曲线峰值强度)和极限状态均有显著的影响。结合图 2 和表 2 可知,随着墩底塑性铰区单元长度 L_{\text{Bot}} 的增大,墩柱的最大水平抗力、位移延性系数和极限位移均逐渐增大。采用 \text{DBE} 模型进行钢筋混凝土墩柱抗震性能分析时,塑性铰区单元长度 L_{\text{Bot}} 对于墩柱最大水平抗力和极限状态的预测有着重要的影响,若墩底塑性铰区单元长度 L_{\text{Bot}} 偏大,则会高估墩柱的位移延性能力,采用该结果指导墩柱的抗震设计是不安全的;若墩底塑性铰区单元长度 L_{\text{Bot}} 偏小,虽然计算结果是偏安全的,但可能会造成其能力过剩,无法充分发挥其抗震性能。因此,确定合理的塑性铰区单元长度 L_{\text{Bot}} 是十分必要的。
2.2 塑性铰区合理单元长度理论分析
为了进一步讨论墩底塑性铰区的合理单元长度,提取上述 5 个 \text{DBE} 模型处于极限状态时各单元各积分点处的截面曲率,绘制各模型的曲率分布图,如图 3 所示。
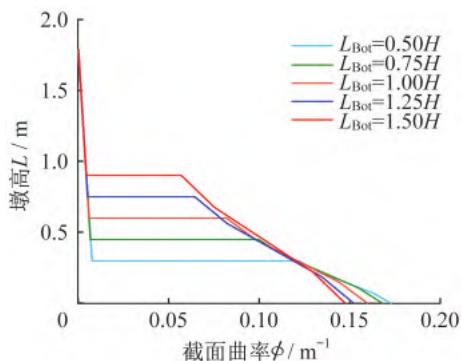
图 3 各模型曲率分布
由图 3 可知,当墩底单元产生塑性变形后,塑性变形集中于该单元内,其余单元始终处于弹性变形阶段,也证明了 \text{Coleman} 和 \text{Spacone}9所提出的观点是合理的。同时也可以发现,图 3 中各 \text{DBE} 模型的曲率分布符合等效塑性铰长度理论的基本假定(图 4),即对于钢筋混凝土墩柱而言,当墩底截面到达极限状态时,沿墩高的实际曲率分布曲线是不规则的,为了便于计算,引入“等效塑性铰长度”的概念,即假设在墩底附近存在一个长度为 L_p 的等塑性曲率段,在该段长度内,截面的塑性曲率等于墩底截面的最大塑性曲率 \phi_p,L_p 为等效塑性铰长度1,17。图 4 中 \phi_y 为截面等效屈服曲率,\phi_u 为截面极限曲率。
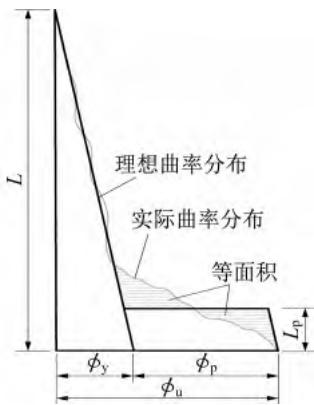
图 4 等效塑性铰长度定义
由上述分析可知,在 \text{DBE} 模型中,塑性铰区合理单元长度可以取等效塑性铰长度 L_p。关于等效塑性铰长度的计算,国内外学者进行了大量的研究,提出了不同的等效塑性铰长度 L_p 经验计算公式18,但是目前被我国《公路桥梁抗震设计规范》(\text{JTG/T}2231\text{-}01\text{—}2020)19采用以及被大多数学者所接受的是 \text{Priestley} 等17提出的等效塑性铰长度经验计算公式,在实际建模过程中,可以采用该经验公式计算塑性铰区单元长度 L_{\text{Bot}},计算公式如下:
式中:L 为悬臂墩高度或塑性铰截面到反弯点的距离;f_y 为纵向钢筋抗拉强度标准值;d_s 为纵向钢筋直径。
3 数值模型的正确性验证
上文主要以 \text{PEER} 结构试验数据库中的弯曲破坏模式的悬臂墩 \text{PA-9} 为依据,基于 \text{OpenSees} 开源平台, 采用 \text{DBE} 建立了其滞回 \text{Pushover} 分析有限元模型。在该模型的基础上, 讨论了当采用 \text{DBE} 模型进行非线性分析时, 塑性铰区单元长度对墩柱弹塑性性能的影响, 并结合墩柱曲率分布数值模拟结果和等效塑性铰长度理论, 确定了塑性铰区的合理单元长度为等效塑性铰长度 L_p。本节主要以墩柱 \text{PA-9} 和 \text{PEER} 结构试验数据库中另外 2 个弯曲破坏模式钢筋混凝土悬臂墩的拟静力试验结果为依据, 来验证上文所提出的数值模型的合理性。
从 \text{PEER} 结构试验数据库中另选 2 个弯曲破坏模式钢筋混凝土悬臂墩,分别为墩柱 \text{Kunnath et al.} 1997\text{, A2}(以下简称 \text{KU-2})和墩柱 \text{Tanaka and Park} 1990\text{, No.5}(以下简称 \text{TA-5}),其几何尺寸和轴向荷载参数详见表 3,墩柱截面构造和数值模型中纤维截面的划分如图 5 所示,纤维截面各材料参数详见表 4。
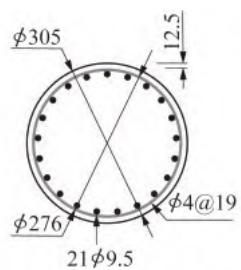
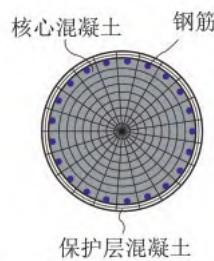
(a) 墩柱 \text{KU-2}
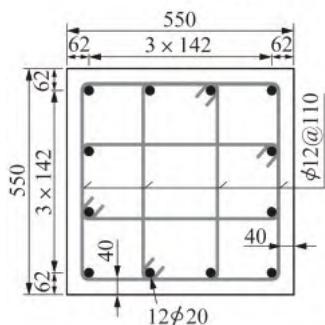
(b) 墩柱 \text{TA-5}
图 5 墩柱截面构造及纤维截面划分(单位:\text{mm})
表 3 墩柱 \text{KU-2} 和 \text{TA-5} 几何尺寸及轴向荷载
| 构件编号 | 截面形式 | 墩高 L/\text{m} | 截面高度 H(D)/\text{m} | L/H | 轴向荷载 P/\text{kN} | 轴压比 n/\% |
|---|---|---|---|---|---|---|
| \text{KU-2} | 圆形截面 | 1.372 | 0.305 | 4.5 | 200 | 9.4 |
| \text{TA-5} | 正方形截面 | 1.650 | 0.550 | 3.0 | 968 | 10.0 |
表 4 墩柱 \text{KU-2} 和 \text{TA-5} 纤维截面材料参数
| 构件编号 | 保护层混凝土 \text{Concrete}04 | 核心混凝土 \text{Concrete}04 | 纵向钢筋 \text{Steel}02 |
|---|---|---|---|
| 抗压强度f_c'/\text{MPa} | 峰值应变\varepsilon_c | 极限应变\varepsilon_u | |
| \text{KU-2} | 29.0 | 0.002 | 0.005 |
| \text{TA-5} | 32.0 | 0.002 | 0.005 |
根据式 (1) 和式 (2) 分别计算 3 个墩柱 \text{DBE} 模型中的零长度转动弹簧刚度 K_{\text{slip}} 和等效塑性铰长度 L_p,将计算结果汇总于表 5。
表 5 零长度转动弹簧刚度和等效塑性铰长度
| 构件编号 | 零长度转动弹簧刚度K_{\text{slip}}/(1.0\times 10^3 \text{kN}\cdot\text{m}\cdot\text{rad}^{-1}) | 等效塑性铰长度L_p/\text{m} |
|---|---|---|
| \text{PA-9} | 326.5 | 0.371 |
| \text{KU-2} | 22.5 | 0.203 |
| \text{TA-5} | 166.5 | 0.357 |
采用图 1 所示建模方法,分别建立 3 个钢筋混凝土悬臂墩的滞回 \text{Pushover} 分析数值模型,墩底塑性铰区单元长度 L_{\text{Bot}} 取表 5 中相应的等效塑性铰长度 L_p,结合试验结果(滞回曲线),以位移控制加载进行滞回 \text{Pushover} 分析,各墩柱滞回曲线、骨架曲线的数值模拟结果及其与试验结果的对比如图 6 所示。
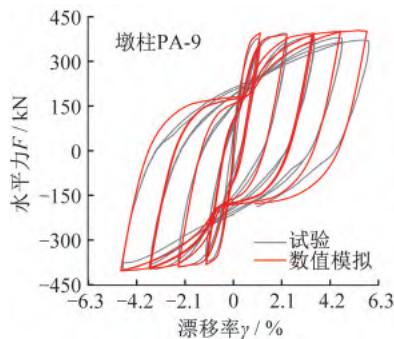
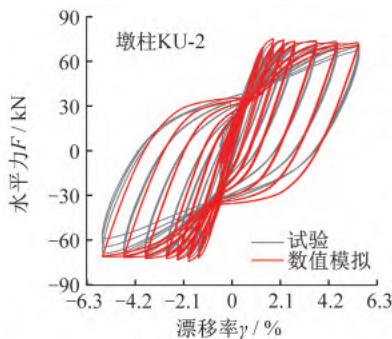
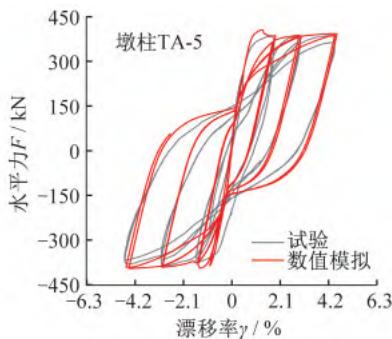
(a) 滞回曲线
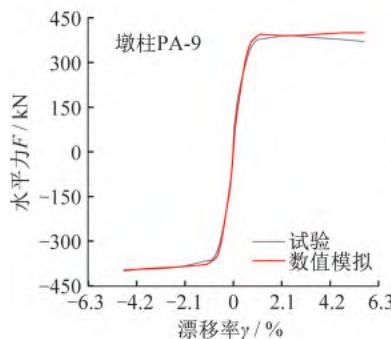
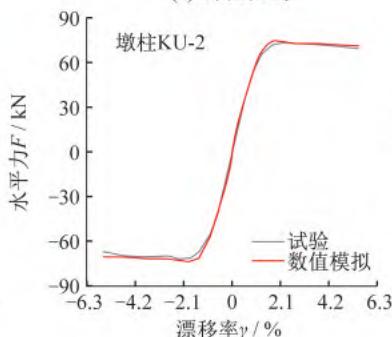
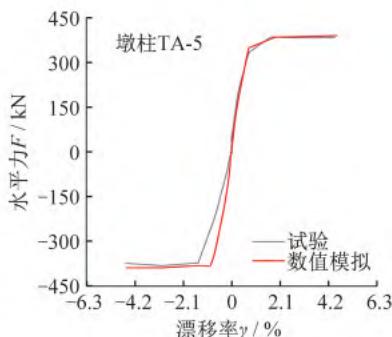
(b) 骨架曲线
图 6 数值模拟结果与试验结果对比
从图 6 可以看出,各墩柱滞回曲线、骨架曲线的数值模拟结果和试验结果基本吻合,对于不同截面形式的钢筋混凝土墩柱,采用该数值模型进行弹塑性分析,均可获得良好的模拟效果,能够比较精确地反映出墩柱的真实侧向刚度和最大水平抗力。
4 结论
基于 \text{OpenSees} 开源平台,采用基于位移的纤维梁柱单元 (\text{DBE}) 和零长度单元建立了考虑钢筋混凝土墩柱弯曲变形和粘结滑移效应的有限元模型,分析了塑性铰区单元长度对墩柱弹塑性性能的影响,探讨了其合理取值,并基于拟静力试验结果进行了数值模型验证,得出了以下结论:
(1) 采用 \text{DBE} 有限元模型分析钢筋混凝土墩柱的弹塑性性能时, 塑性铰区单元长度对墩柱的最大水平抗力和位移延性的预测有着显著的影响。若塑性铰区单元长度偏大, 则会高估墩柱的最大水平抗力和位移延性; 反之, 会低估墩柱的最大水平抗力和位移延性。
(2)采用 \text{DBE} 建模时,墩柱塑性铰区的合理单元长度为等效塑性铰长度。
(3) 采用 \text{DBE} 和零长度单元建立钢筋混凝土墩柱的有限元模型,并采用 \text{Priestley} 等17提出的等效塑性铰长度经验公式确定塑性铰区单元长度,能够比较精确地模拟墩柱的弹塑性性能。
参考文献
叶爱君, 管仲国. 桥梁抗震 [M]. 北京: 人民交通出版社, 2017. \text{YE Aijun, Guan Zhongguo}. \text{Seismic design of bridges} [M]. \text{Beijing}: \text{China Communications Press}, 2017. (\text{in Chinese}) ↩ ↩ ↩ ↩
李贵乾, 郑罡, 高波. 基于 OpenSees 的钢筋混凝土桥墩拟静力试验数值分析 [J]. 世界地震工程, 2011, 27(1):110-114. \text{LI Guiqian, ZHENG Gang, GAO Bo}. \text{Numerical analysis for pseudo-static tests of reinforced concrete bridge columns based on OpenSees} [J]. \text{World Earthquake Engineering}, 2011, 27(1): 110\text{-}114. (\text{in Chinese}) ↩
\text{ZERIS C A, MAHIN S A}. \text{Analysis of reinforced concrete beam-columns under uniaxial excitation} [J]. \text{Journal of Structural Engineering, ASCE}, 1988, 114 (4):804\text{-}820. ↩
\text{SPACONE E, FILIPPOU F C, TAUCER F F}. \text{Fibre beam-column model for nonlinear analysis of R/C frames I: Formulation}[J].\text{Earthquake Engineering and Structure Dynamics}, 1996, 25(7): 711\text{-}725. ↩
赫中营, 叶爱君. 力法非线性梁柱单元的合理单元长度划分 [J]. 工程力学, 2014, 31(7):178-184,198. \text{HE Zhongying, YE Aijun}. \text{Reasonable discrete element length of force-based nonlinear beam-column elements} [J]. \text{Engineering Mechanics}, 2014, 31 (7): 178\text{-}184, 198. (\text{in Chinese}) ↩
\text{SCOTT M H, FRANCHIN P, FENVES G L, et al}. \text{Scott et al}. \text{Response sensitivity for nonlinear beam-column elements} [J]. \text{Journal of Structural Engineering}, 2004, 130(9):1281\text{-}1288. ↩
\text{TERZIC V}. \text{Force-based element vs. displacement-based element} [R]. \text{University of Berkeley, OpenSees, NEES, \& NEEScomm}, 2011. ↩ ↩ ↩
伍永飞. 钢筋混凝土框架结构静力非线性分析程序研制 [D]. 上海:同济大学,2007. \text{WU Yongfei}. \text{The nonlinear FEA program of RC frame structures} [D]. \text{Shanghai}: \text{Tongji University}, 2007. (\text{in Chinese}) ↩
\text{COLEMAN J, SPACONE E}. \text{Localization issues in force based frame elements} [J]. \text{Journal of Structural Engineering}, 2001, 127(11): 1257\text{-}1265. ↩ ↩ ↩
赵泰儀, 孙治国, 石岩, 等. 基于纤维梁柱单元的桥梁墩柱地震反应模拟方法研究 [J]. 世界地震工程, 2019, 35(1): 117-127. \text{ZHAO Taiyi, SUN Zhiguo, SHI Yan, et al}. \text{Research on the simulation method for the seismic responses of bridge piers by using fiber beam-column elements} [J]. \text{World Earthquake Engineering}, 2019, 35 (1): 117\text{-}127. (\text{in Chinese}) ↩ ↩
\text{MANDER J B, PRIESTLEY M J N, PARK R}. \text{Theoretical stress-strain model for confined concrete} [J]. \text{Journal of Structural Engineering}, 1988, 114(8): 1804\text{-}1826. ↩
\text{FILIPPOU F C, POPOV E P, BERTERO V V}. \text{Effects of bond deterioration on hysteretic behaviour of reinforced concrete joints} [R]. \text{Berkeley}: \text{University of California}, 1983. ↩
高健峰, 李建中, 梁博. 考虑粘结滑移效应的墩柱低周往复加载模拟方法 [J]. 工程力学, 2023, 40(2): 74-84. \text{GAO Jianfeng, LI Jianzhong, LIANG Bo}. \text{Simulation method of low cycle reciprocating loading of pier column considering bond-slip effect} [J]. \text{Engineering Mechanics}, 2023, 40(2):74\text{-}84. (\text{in Chinese}) ↩
\text{ELWOOD K J, EBERHARD M O}. \text{Effective stiffness of reinforced concrete columns} [J]. \text{ACI Structural Journal}, 2009, 106(4):476\text{-}484. ↩ ↩ ↩
\text{ZHAO J, SRITHARAN S}. \text{Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structure} [J]. \text{ACI Structural Journal}, 2007, 104(2):133\text{-}141. ↩
\text{TAZARV M}. \text{Next generation of bridge columns for accelerated bridge construction in high seismic zones} [M]. \text{Nevada}: \text{University of Nevada, Reno}, 2014. ↩
\text{PRIESTLEY M J N, SEIBLE F, CALVI G M}. \text{Seismic design and retrofit of bridges} [M]. \text{New York}: \text{John Wiley \& Sons}, 1996. ↩ ↩ ↩ ↩
邵长江, 孙南昌, 佐雪, 等. 矩形截面混凝土空心墩塑性铰长度分析 [J]. 土木工程学报, 2018, 51(11): 120-128. \text{SHAO Changjiang, SUN Nanchang, ZUO Xue, et al}. \text{Study on plastic hinge length of rectangular hollow-section concrete pier} [J]. \text{China Civil Engineering Journal}, 2018, 51(11):120\text{-}128. (\text{in Chinese}) ↩
中华人民共和国交通运输部. 公路桥梁抗震设计规范: JTG/T 2231-01—2020[S]. 北京: 人民交通出版社, 2020. \text{Ministry of Transport of the People's Republic of China}. \text{Specifications for seismic design of highway bridges}: \text{JTG/T} 2231\text{-}01\text{—}2020 [S]. \text{Beijing}: \text{China Communications Press}, 2020. (\text{in Chinese}) ↩