王晓伟,钱晋,叶爱君,王靖程,杨光怡
(同济大学土木工程防灾减灾全国重点实验室,上海 200092)
摘要:桩柱式墩是桥梁工程中广泛采用的下部结构形式,但如果桩身没有进行有效的能力保护设计,在地震作用下可能形成塑性铰。而且,由于土桩动力相互作用的复杂影响,如何根据墩柱塑性铰区截面的超强弯矩计算桩身的抗震需求,依然是桩柱式墩桥梁延性抗震设计中的技术难题。为此,本文基于土 - 桩 - 结构一体化模型,对桩柱式墩桥梁的延性抗震设计方法开展研究,重点解决桩身地震需求的简化计算问题。通过开展不同地震强度下桩柱弯矩分布发展规律研究,确定了桩身地震需求参数;通过桩身地震需求参数敏感性分析,结合大量参数分析及多元线性回归方法,建立了桩身地震需求参数与土体、结构参数之间的关联关系,提出了基于能力保护的桩身抗弯需求和加强配筋范围的简化计算方法。研究成果可为我国桩柱式墩桥梁延性抗震设计方法的改进提供依据。
关键词:桥梁工程;桩柱式墩桥梁;桩身地震需求;能力保护构件;简化计算方法
中图分类号: \mathrm{U}442.5 + 5
文献标识码:A
文章编号:10.6052/j.issn.1000-4750.2022.10.0850
SIMPLIFIED SEISMIC DEMAND PREDICTION METHOD FOR EXTENDED PILE-SHAFTS IN COHESIONLESS SOILS
WANG Xiao-wei, QIAN Jin, YE Ai-jun, WANG Jing-cheng, YANG Guang-yi
(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: The pile-shaft is a substructure widely used in bridge engineering. Under earthquake, the pile may yield if the capacity protection design principle is not well followed. In addition, due to the complex soil-pile interaction in modeling and analysis, it is still difficult to predict the seismic demand of piles based on the yielding moments of piers. Therefore this study adopts a coupled soil-pile-structure model to investigate the ductility seismic design method of pile-shafts with a focus on the simplified seismic demand prediction method. Investigations are conducted on the bending moment distribution under different earthquake intensities to determine pile-shaft demand parameters, and extensive parametric analyses are performed to understand the mathematical relationship between pile-shaft demand parameters and soil/structural sensitive parameters. Finally, a simplified seismic demand prediction method is proposed.
Keywords: bridge engineering; extended pile-shaft bridge; pile-shaft seismic demand; capacity-protection component; simplified calculation method
鉴于经济性和施工便利性,桩柱式桥墩是我国中小跨径桥梁最常用下部结构形式之一。以往研究1,2,3,4,5通过理论研究、现场试验、震害调研与分析等表明,如果桩柱式桥墩的桩身没有进行有效的能力保护设计,桩身在地震下可能形成塑性铰。国外桥梁抗震设计规范允许桩身产生有限损伤6,7,8。但是,我国现行的桥梁抗震设计规范9,10对桩基础采用能力保护的抗震设计策略,在 E2 地震作用下仅允许桥墩进入屈服状态,而桩基则必须保持弹性状态。因此,准确预测桩身的最大地震需求、明确桩身加强配筋的范围是桩柱式墩桥梁延性抗震设计的关键。考虑到土桩动力相互作用模拟和分析的复杂性,桩柱式桥墩在 E2 地震下的延性抗震设计实践中,通常将墩柱和桩基础分别建模分析,即墩柱模型中桩基础以等代弹簧考虑,通过地震反应分析得到墩底内力,并考虑超强系数后将墩底轴力、超强弯矩和剪力作为外荷载输入基于温克乐地基梁理论的桩基础模型,进行静力分析。整个过程十分复杂。由此可见,如何根据桥墩塑性铰区截面的超强弯矩快速有效地获得桩身的地震需求,从而将设计人员从繁琐的有限元建模分析中解放出来,仍然是桩柱式墩桥梁延性抗震设计中亟待攻克的关键技术难题。这也是本文的研究目标。
国内外学者针对桩柱式桥墩地震需求和抗震行为进行了相关研究。Budek 等11采用沿桩身布置若干作动器的方式模拟土体外部约束,探究了桩身的弹塑性行为,但该模拟方法忽略了土体、桩身进入非线性后内力重分布的问题。Chai1将桩柱式墩简化为等效嵌固模型,采用理论推导揭示了桩柱整体位移延性需求与桩身局部曲率延性需求的关联关系,并采用现场试验进行了验证2。Gerolymos 等12采用动力有限元分析,建立了桩柱式墩整体位移延性与桩身局部曲率延性的数学模型。Zhang 等13采用 Pushover 数值分析,研究了给定位移延性目标下桩柱式墩的桩身局部曲率延性需求和等效塑性铰长度。刘腾飞等14采用循环往复的 Pushover 数值分析,研究了砂土相对密实度对桩柱式桥墩桩身塑性铰长度的影响。董召先等15采用非线性动力分析研究了地震作用下液化场地桩柱式墩的残余位移。从上述文献回顾可知,考虑土桩相互作用的试验和数值分析仍然是桩柱式桥墩抗震行为研究的主要手段16,而针对桩身作为能力保护构件的桩柱式桥墩地震需求简化计算方法的研究仍比较欠缺。特别值得说明的是,以往研究中通常假定墩径与桩径相同,而我国桥梁工程中桩柱式桥墩存在大量的桩径大于墩径的情况。因此很有必要开展不同墩、桩径的桩柱式墩桥梁桩身地震需求简化计算方法研究。
本文旨在建立桩柱式墩桥梁桩身地震需求的简化计算方法。首先介绍土 - 桩 - 结构一体化模拟方法和采用的地震动输入。然后研究桩柱弯矩分布规律,并定义桩身地震需求关键参数。在此基础上,研究场地、桩柱桥梁参数中对结构地震需求参数影响的高、低敏感性参数。最后,通过大量参数分析,结合多元线性回归方法,建立桩身地震需求的简化计算方法。
1 土-桩-结构一体化模拟方法及验证
1.1 研究对象及其数值建模方法
本文研究对象为原土场地常用的桩柱式单墩桥梁,这类中小跨径桥梁的特点是:各墩墩高和截面尺寸相同,且由于跨径较小,各墩场地条件接近,故而各墩的动力特性相近。因此,桥梁可简化为单墩模型进行抗震分析,如图 1 所示。桩柱通常采用钢筋混凝土实心截面,桩身直径略大于墩身,埋置深度通常很深,足够产生弯矩反弯点。参考以往研究17,18,影响这类桥梁地震反应的参数主要包括:墩高 L_{c} 、墩径 D_{c} 、轴压比 R_{ac} 、桩径 D_{p} 、截面配筋率 \rho_{l} 、配箍率 \rho_{s} 、以及砂土相对密实度 D_{r} 。
基于 OpenSees19平台,建立研究对象的土 - 结构一体化数值模型,如图 1 所示。上部结构以集中质量 M_{a} 替代,由 R_{ac} 、混凝土抗压强度标准值 f_{c} 、桥墩截面面积 A_{g} 确定,即 M_{a} = R_{ac} f_{c} A_{g} / g 。由于本文旨在确定桩柱式墩桥梁中作为能力保护构件的桩身的地震需求,桩基础采用弹性梁柱单元模拟,而桥墩采用基于位移的非线性梁柱单元辅以纤维截面模拟:单元划分取 1 倍墩径,每个单元取 5 个积分点,纤维截面的钢筋和混凝土分别采用 Steel02 和 Concrete04 材料模拟,核心混凝土的本构参数通过 Mander 模型20确定,纤维截面的划分方式为保护层和核心混凝土径向分别按 1 份和 8 份划分,而周向均划分为 10 份,这样的模拟方法可得到可靠的墩柱曲率反应21。此外,由于本文专注桥墩的延性抗震设计,模型中不考虑支座等墩梁连接部件。
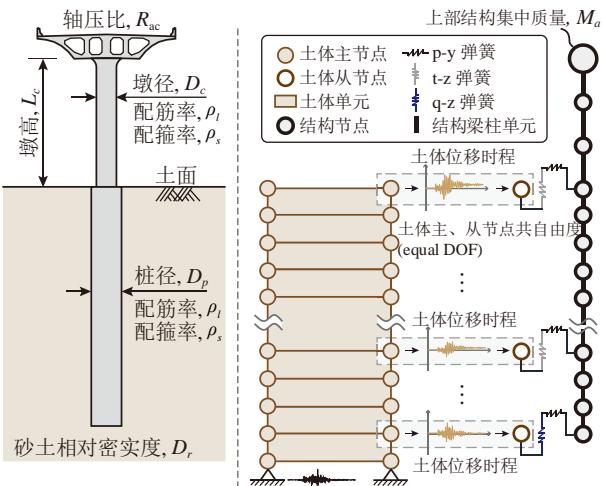
图 1 研究对象 (左) 及其数值建模(右)
Fig.1 Study object (left) and numerical model (right)
基于平面应变假定和一维剪切梁模型,土体采用四节点 Quad 单元模拟 (图 1)。每一层土按 0.5\mathrm{m} 厚度划分,该厚度可保证实际地震波的有效传播22。相同深度的土体两侧节点共自由度,土体底面节点约束水平及竖向自由度。桩身单元相应地按 0.5\mathrm{m} 进行划分23,土柱相互作用采用非线性弹簧连接。土体的非线性力学行为采用 PDMY 材料模拟,各参数的取值方法见 Wang 等24,其中影响砂土静动力特性的密度、剪切模量、内摩擦角等参数随相对密实度 D_{r} 的变化而变化。
土桩水平向相互作用采用 PySimple1 材料模拟 API 规范25推荐的砂土 p - y 关系:
式中: p(y) 为土层深度 h 处土 - 桩相对位移 y 时的桩侧土压力; A 为荷载系数 (循环荷载取 0.9); k 为地基反力系数,可根据砂土相对密实度 (D_r) ,通过 API 规范25确定; p_u 为极限土体抗力,按以下公式确定25:
式中: C_1 , C_2 , C_3 为系数,计算方法见文献26; \gamma 为土的有效重度。
桩侧竖向土桩相互作用采用 TzSimple1 材料模拟 Mosher27提出的 t - z 关系:
式中: t(z) 为土桩竖向相对位移 z 时的桩侧摩阻力; E_{f} 为桩侧摩阻力的初始模量,是内摩擦角的函数,采用 Mosher27推荐值; t_u 为桩侧极限摩阻力28:
式中, \phi 为以弧度为单位的内摩擦角。
桩尖竖向土桩相互作用采用 QzSimple1 材料模拟 Meyerhof29提出的单压 q - z 关系:
式中: q(z) 为土与桩尖相对位移 z 时的桩尖抗力; z_{eq} = 0.05D_p29 为土抗力达到峰值 q_{ult} 时的位移; q_{ult} 按下式确定: q_{u} = N_{q}\gamma h
式中, N_{q} 为桩尖竖向承载力系数,按文献29确定。
采用瑞利阻尼模拟土 - 结构一体化模型的阻尼特征。瑞利阻尼由质量阻尼和刚度阻尼组成,阻尼系数由振型参与质量系数最大的前两阶振型确定。特别需要强调的是,刚度阻尼应根据模型的“当前刚度”确定,而非“初始刚度”,即 OpenSees 中瑞利阻尼设置为当前刚度项,而非初始刚度项,否则可能导致强震下桩柱在介质突变处 (比如土面) 出现弯矩分布不连续的非正常情况。场地底部认为假象基岩面,地震动加速度时程从场地底部输入,进行非线性地震反应分析。
1.2 数值模拟方法验证
上述土 - 结构一体化建模方法采用 UCDavis 完成的离心机试验 CSP3 进行验证。如图 2 所示,桩柱式墩模型置于砂土场地的剪切土箱中,土箱底部的地震输入为 SantaCruz 波,峰值加速度 (PGA) 0.49\mathrm{g}30 。为缩减篇幅,数值模型参数取值见作者以往文献24,但考虑到文本表述逻辑的连贯性和完整性,图 3 给出了试验结果和数值模型的对比结果,总体上时程反应得到了很好的再现,其中上部结构加速度峰值和桩身最大弯矩的误差均在 10\% 以内,而上部结构位移峰值的误差为 26\% 。考虑到本文重点关注桩身的最大弯矩反应,所采用的数值模型是可靠的。
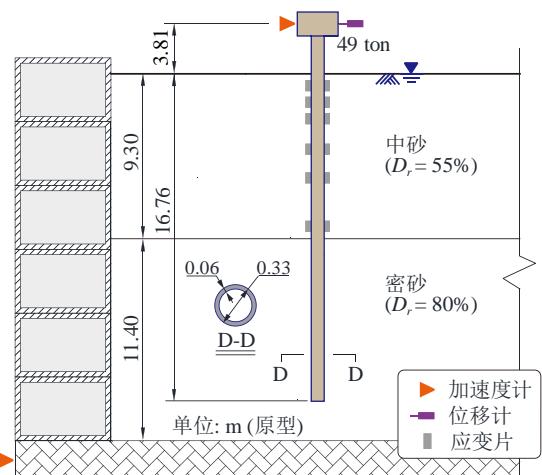
图 2 CSP3 桩柱式墩结构地震反应离心机模型试验
Fig.2 CSP3 centrifuge test model of extended pile-shaft-supported structure
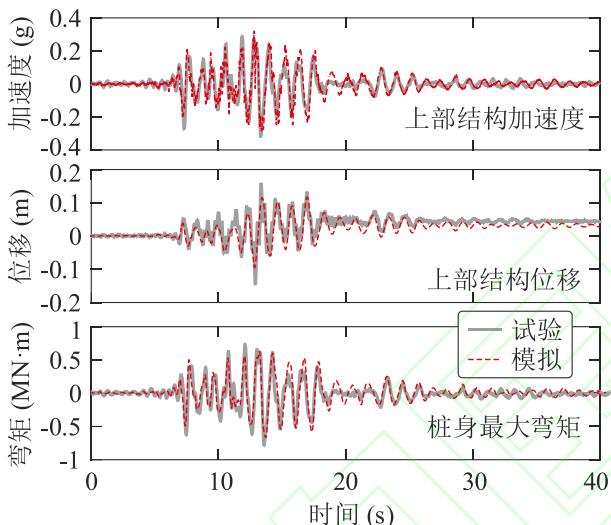
图 3 离心机试验结果与数值模拟结果对比
Fig.3 Comparison between centrifuge and simulation results
2 地震动输入
对于不同工况,采用 Baker 等31选取的 40 条岩石场地地震记录作为地震动输入。这 40 条波对应的加速度反应谱见图 4,从竖轴看,该组地震记录的 PGA 介于 0.06\mathrm{g}\sim 1.0\mathrm{g} 之间 (即竖轴截距),反应谱峰值介于 0.2\mathrm{g}\sim 2.5\mathrm{g} 之间,从横轴看,该组地震记录频谱特性差异较大。以我国《公路桥梁抗震设计规范》9中桥梁重要性分类为据,图 4 还给出了桩柱式墩较常用的 B 类和 C 类桥梁的最大、最小 E2 设计反应谱,以及下文算例桥梁的 E2 设计反应谱。由图可知,40 条地震记录的反应谱基本介于桩柱式墩桥梁的最大、最小 E2 设计反应谱之间;算例桥梁的 E2 设计反应谱与这些反应谱的均值较接近。因此,这 40 条地震记录以及下文考虑的土体和结构参数所形成的工况可涵盖工程中的绝大多数情况。
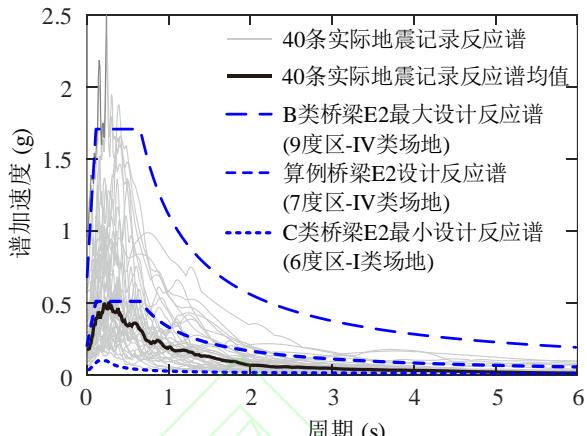
图 4 40 条地震记录加速度反应谱及其与设计反应谱的比较
Fig.4 Acceleration response spectra of the 40 ground motions and the design spectra
3 桩柱弯矩分布发展规律
3.1 不同PGA下的桩身弯矩分布规律
本节以我国华东地区高速公路某典型桩柱式墩桥梁为例 (主要参数见图 5(a)),研究不同 PGA 下桩柱弯矩分布发展规律 (图 5(b))。地震动输入采用前述 40 条地震动输入中的 1971 年 San Fernando 地震动。由图 5 可见,随着 PGA 的增加,桩柱弯矩最大值不断增加,但增加幅度逐渐减小,特别是 PGA 从 0.7\mathrm{g} 增大到 0.9\mathrm{g} 时弯矩增幅很小,说明墩柱已屈服;换言之,该图展示了典型桩柱式墩的弹塑性弯矩发展规律。从图 5(b) 还可知,桩身最大弯矩埋深、土面以下弯矩反弯点埋深受 PGA 的影响很小。为进一步说明该现象,图 5(c) 给出了高程和弯矩标准化后的结果,即高程除以桩径,而弯矩除以墩底弯矩。由图可知,桩身最大弯矩与墩底弯矩的比值、最大弯矩埋深、以及弯矩反弯点埋深均几乎不受 PGA 的影响,即这三个可表征桩身地震需求的参数与桩柱是否屈服无关。
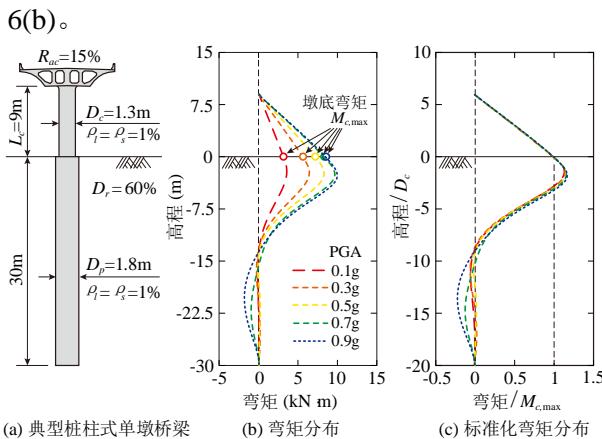
图 5 不同 PGA 下的桩柱弯矩分布发展规律
Fig.5 Development of bending moment distribution of the extended pile-shaft under different PGA levels
3.2 桩身地震需求参数定义
基于上述发现,从桩身按能力保护构件设计的角度出发,本文考虑的桩身地震需求参数包括:桩身最大弯矩 (M_{p,\mathrm{max}}) ,最大弯矩所在深度 (H_{p}) ,以及土面以下弯矩反弯点深度 (L_{p}) ,如图 6 所示。为得到通用性结论,这些地震需求参数以标准化方式表达,见式 (7),其中, \overline{H_{p}} 和 \overline{L_{p}} 可用于保守地确定桩身加强配筋的范围,见图。
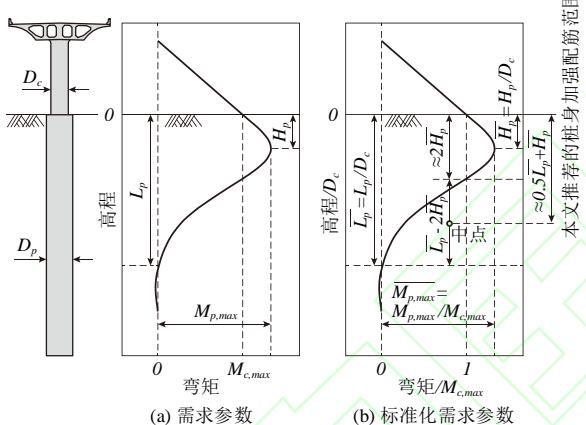
图 6 桩柱弯矩分布及桩身地震需求参数定义
Fig.6 Bending moment distribution of extended pile-shaft and definition of seismic demand parameters
4 桩身地震需求参数敏感性分析
4.1 敏感性分析参数取值
确定影响结构地震需求参数的高、低敏感性参数是建立可靠且简洁数学模型的重要前提。为此,本节对前述的桩柱式墩桥梁关键参数(或标准化参数 )进行了敏感性分析。由于工程中钢筋和混凝土型号相对固定,且以往研究表明钢筋、混凝土强度参数不是桩基地震需求的高敏感性参数,故在本文敏感性分析中不考虑(模型中混凝土抗压强度取 30MPa,钢筋屈服强度取 400MPa)。分析参数取值见表 1,中间值和上、下限取值在调研了我国几十座桩柱式墩桥梁所确定。中间值组成的工况为基本工况,在基本工程基础上,每次改变一个参数为其上限或下限值,共形成 13 个工况。每个工况下结构地震响应取前述 40 条地震动下结果的平均值,共进行 13\times 40 = 520 次非线性地震反应分析。
表 1 敏感性分析参数取值
Table 1 Parameters in sensitivity analysis
| # | 参数 | 中间值 | 上、下限值 |
|---|---|---|---|
| 1 | 相对密实度,D_r(%) | 58.5 | 80.8、35.0 |
| 2 | 标准化墩高,\overline{L_c} | 6 | 8、2 |
| 3 | 标准化桩径,\overline{D_p} | 1.25 | 1.40、1.10 |
| 4 | 桩柱配筋率,\rho_l(%) | 1.00 | 1.25、0.75 |
| 5 | 桩柱配箍率,\rho_s(%) | 1.00 | 1.25、0.75 |
| 6 | 轴压比,R_{ac} | 0.15 | 0.20、0.10 |
4.2 参数敏感性分析原理
为降低各参数上、下限幅值差异化对参数敏感性分析的影响,采用 Ahmed 和 Dasgupta32提出的敏感性指标 SI 来量化各参数的敏感性:
式中: I_{1} 和 I_{2} 为同一参数的两个不同输入值 (I_2 > I_1 ,即各参数的中间值和上限,或下限和中间值 ); O_{1} 和 O_2 为对应的地震需求参数; Mean(*) 为返回平均值的函数。若 SI 为正,则需求参数随变量的增大而增加,反之若 SI 为负,则需求参数随变量的增大而减小。
4.3 参数敏感性计算结果
图 7 给出了 6 个参数对标准化结构地震需求参数 (\overline{M_{p,\mathrm{max}}}, \overline{H_{p}}, \overline{L_{p}}) 的敏感性指标 SI ,并按 SI 的绝对值从上至下排列, SI 绝对值越大则敏感性越高。由图可知,标准化墩高、桩径、土体相对密实度为高敏感性参数,而桩柱的配筋率、配箍率及轴压比为低敏感性参数。因此,下文在建立结构地震需求参数的数学模型时主要考虑高敏感性参数。从 SI 的正负结果上看,墩高越高,标准化桩身最大弯矩 \overline{M_{p,\mathrm{max}}} 越小,这是因为墩高越高,桩身最大弯矩埋深越浅,即桩身达到最大弯矩所需的土抗力深度范围越小,因此桩身最大弯矩与墩底弯矩越接近,即标准化桩身最大弯矩越小;同理,相对密实度越大,桩身最大弯矩埋深和反弯点埋深越浅,标准化桩身最大弯矩越小;桩径变大,桩身最大弯矩和桩身最大弯矩埋深与反弯点埋深略有增加。
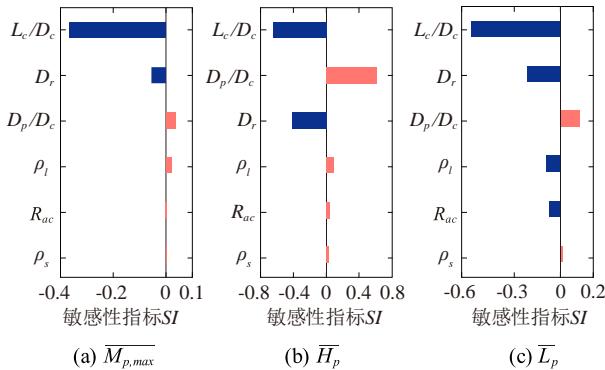
图 7 场地、结构参数对不同地震需求参数的敏感性
Fig.7 Sensitivity of examined parameters to structural demand parameters
5 桩身地震需求简化计算方法
5.1 高敏感性参数分析工况
为构建用于建立桩身地震需求参数数学模型的数据库,且尽可能覆盖工程中桩柱式墩桥梁的情况,以实际工程中最常用的墩径 D_{c} = 1.5\mathrm{m} 为基准,表 2 列出了所考虑的高敏感性参数的取值范围,每个参数取 4 个值。对所有取值进行全排列,共形成 4\times 4\times 4 = 64 个工况,每个工况采用 40 条地震动进行加载,共形成 2560 次非线性地震反应分析。
表 2 所考虑的高敏感性参数及其取值
Table 2 Sensitive parameters and values
| 参数 | 符号 | 取值 |
|---|---|---|
| 砂土相对密实度(%) | D_r | 35、50、65、80 |
| 标准化墩高(L_c/D_c) | \overline{L_c} | 4、6、8、10 |
| 标准化桩径(D_p/D_c) | \overline{D_p} | 1.1、1.2、1.3、1.4 |
5.2 桩身地震需求参数计算公式建立及检验
为建立桩身地震反应计算公式,从结构物理力学基本关系出发构建拟合公式。桩身地震反应主要取决于结构刚度和土抗力。众所周知,结构刚度与墩高的三次方成反比,与截面直径的四次方成正比,而土抗力与砂土相对密实度成正相关关系。因此,以 1 / \overline{L_c}^3 、 \overline{D_p}^4 、 D_r 、 \overline{L_c} 为变量,采用前述 2560 个非线性地震反应结果为训练集,得到桩身地震需求的拟合公式如下:
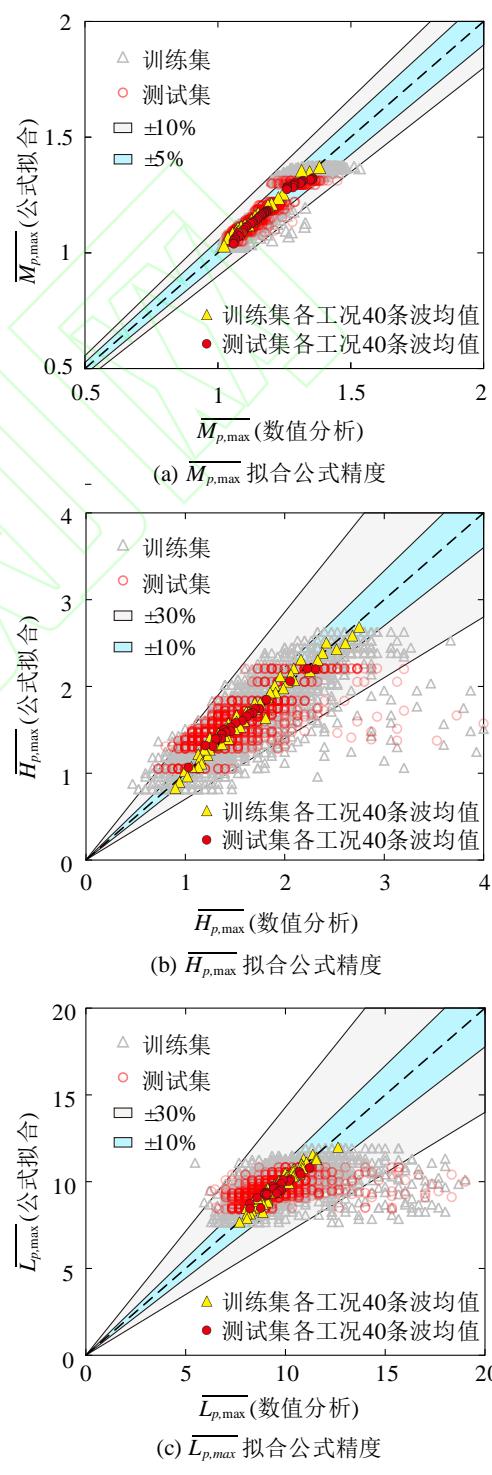
图 8 标准化需求参数拟合公式的精度
Fig.8 Precision of the fitting formula for standardized demand parameters
为检验拟合公式的准确度,在表 2 所列的参数上、下边界范围内,随机抽取 23 组工况(与训练集的 64 组工况不重叠 ),每组进行 40 次非线性地震反应分析,共形成 23\times 40 = 920 个数据作为测试集。
根据训练集和数据集的计算结果,图 8 给出了桩身地震需求参数的数值分析结果和公式拟合结果对比。由图可知, \overline{M_{p,\mathrm{max}}} 的拟合精度很高,训练集和测试集的结果误差基本都在 10\% 以内;相比之下, \overline{H_p} 和 \overline{L_p} 的拟合精度稍低,但绝大多数结果的误差仍在 30\% 以内。尽管如此,40 条地震记录的均值反应对所提出公式的拟合精度极高,误差均在 10\% 以内。值得说明的是,在实际工程中,桩身最大弯矩是延性抗震设计最关键的需求参数,预测精度要求高,而最大弯矩深度和反弯点深度主要用于确定加强配筋的范围,预测精度要求相对较低。因此,本文提出的拟合公式基本满足工程要求。
5.3 基于能力保护的桩身最大弯矩需求和加强配筋范围确定方法
从桩身能力保护构件的角度出发,桩身的最大地震弯矩需求 M_{p,\mathrm{max}} 可按下式计算:
式中: M_{y,c} 为墩底截面在恒载作用下从弯矩曲率分析中得到的等效屈服弯矩; \phi 为超强系数,可取 1.29 ,即 \phi M_{y,c} 为墩柱塑性铰区截面的超强弯矩。回顾图 6,土面以下桩身加强配筋范围 L_{R} 可按下式估算:
结合前述图 8 的结果,可初步判断,桩身最大弯矩需求的计算误差控制在 10\% 以内,而桩身加强配筋范围计算误差基本控制 30\% 以内。
6 结论
本文基于土 - 桩 - 结构一体化模型,研究了不同地震动强度下桩柱弯矩分布发展规律,揭示了桩柱式墩桥梁地震需求的敏感性参数,建立了桩身弯矩需求与土体、结构参数之间的关联关系,提出了作为能力保护构件的桩身抗弯需求简化计算方法。主要结论如下:
(1)桩身反弯点深度及最大弯矩深度随地震动峰值加速度的变化几乎可以忽略;虽然最大弯矩随加速度峰值加速度的增大而增大,但其与墩底最大弯矩的比值几乎不变。
(2)墩高与墩径的比值、桩径与墩径的比值、以及土体相对密实度是桩柱式墩桥梁桩身地震需求的高敏感性参数,而桥墩轴压比和桩柱截面配筋率、配箍率是低敏感性参数。
(3)墩高越高,桩身最大弯矩越小,桩身最大弯矩埋深和反弯点埋深越浅;相对密实度越大,桩身最大弯矩越小,桩身最大弯矩埋深和反弯点埋深越浅;桩径变大,桩身最大弯矩和桩身最大弯矩埋深与反弯点埋深略有增加。
(4)提出的桩身地震需求计算公式在工程应用可接受的范围内,其中桩身最大弯矩需求的计算误差控制在 10\% 以内,而桩身加强配筋范围计算误差基本控制在 30\% 以内。
本文结论限于非液化砂土场地桩柱式单墩桥梁。下一步研究将拓展到砂土液化及侧扩场地。
参考文献
CHAI Y H. Flexural strength and ductility of extended pile-shafts. I: analytical model[J]. Journal of Structural Engineering, 2002, 128(5): 586-594. ↩ ↩
CHAI Y H, HUTCHINSON T C. Flexural strength and ductility of extended pile-shafts. II: experimental study[J]. Journal of Structural Engineering, 2002, 128(5): 595-602. ↩ ↩
HAN Q, DU X, LU J, et al. Seismic damage of highway bridges during the 2008 Wenchuan earthquake[J]. Earthquake Engineering and Engineering Vibration, 2009, 8(2): 263-273. ↩
KAWASHIMA K, TAKAHASHI Y, GE H, et al. Reconnaissance report on damage of bridges in 2008 Wenchuan, China. Earthquake[J]. Journal of Earthquake Engineering, 2009, 13(7): 965-996. ↩
WEI X, WANG Q, WANG J. Damage patterns and failure mechanisms of bridge pile foundation under earthquake[C]//14th World Conference on Earthquake Engineering. Beijing, China: IAEE, 2008. ↩
CALTRANS. Caltrans Seismic Design Criteria Version 2.0[S]. Sacramento, CA: California Department of Transportation, 2019. ↩
JRA. Specifications for highway bridges[S]. Tokyo, Japan: Japan Road Association, 2019. ↩
AASHTO. Guide Specifications for LRFD Seismic Bridge Design[S]. Washington D.C.: American Association of State Highway and Transportation Officials, 2017. ↩
中华人民共和国交通运输部. JTG/TB 02-01-2008 公路桥梁抗震设计细则 [S]. 北京: 人民交通出版社, 2008. (Ministry of Transport, PRC. JTG/TB 02-01-2008 Rules for Seismic Design of Highway and Bridge [S]. Beijing: China Communications Press, 2008. (in Chinese)) ↩ ↩ ↩
中华人民共和国住房和城乡建设部. CJJ 166-2011, 城市桥梁抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2011. (Ministry of Housing and Urban-Rural Development, PRC. CJJ 166-2011, Code for Seismic Design of Urban Bridges [S]. Beijing: China Architecture and Building Press, 2011. (in Chinese)) ↩
BUDEK A M, PRIESTLEY M J N, BENZONI G. The effect of external confinement on flexural hinging in drilled pile shafts[J]. Earthquake Spectra, 2004, 20(1): 1-24. ↩
GEROLYMOS N, DROSOS V, GAZETAS G. Seismic response of single-column bent on pile: Evidence of beneficial role of pile and soil inelasticity[J]. Bulletin of Earthquake Engineering, 2009, 7: 547-573. ↩
ZHANG J, HUTCHINSON T C. Inelastic pile behavior with and without liquefaction effects[J]. Soil Dynamics and Earthquake Engineering, 2012, 36: 12-19. ↩
刘腾飞, 叶爱君, 王晓伟. 土体约束对桩柱式桥墩塑性较长度的影响 [J]. 同济大学学报 (自然科学版), 2016, 44(10): 1490-1496. (LIU Tengfei, YE Aijun, WANG Xiaowei. Confinement effect of soil on plastic hinge length in extended pile-shafts[J]. Journal of Tongji University (Natural Science), 2016, 44(10): 1490-1496. (in Chinese)) ↩
董召先, 孙治国, 李宏男等. 液化场地钢筋混凝土桥墩残余位移分析 [J/OL]. 工程力学, 2022. https://kns.cnki.net/kcms/detail/11.2595. O3.20221024.18.13.482. html. (DONG Zhaoxian, SUN Zhiguo, LI Hongnan, et al. Analysis on residual displacement of reinforced concrete bridge piers standing in liquefiable field[J/OL]. Engineering Mechanics, 2022. https://kns.cnki.net/kcms/detail/11.2595. O3.20221024.18.13.482. html. (in Chinese)) ↩
谢文, 何天涛, 孙利民. 带剪切连梁双柱式桥墩地震响应特性振动台试验研究 [J]. 工程力学, 2021, 38(5): 171-181. (XIE Wen, HE Tiantao, SUN Limin. Shaking table tests on the seismic response characteristics of double-column piers with shear beams [J]. Engineering Mechanics, 2021, 38(5): 171-181. (in Chinese)) ↩
王晓伟, 叶爱君, 罗富元. 液化场地桩柱式基础桥梁结构地震反应的敏感性分析 [J]. 工程力学, 2016, 33(8): 132-140. (WANG Xiaowei, YE Aijun, LUO Fuyuan. Seismic response sensitivity analysis of pile supported bridge structure in liquefiable ground [J]. Engineering Mechanics, 2016, 33(8): 132-140. (in Chinese)) ↩
王晓伟, BLANCO G, 叶爱君等. 砂土中桥梁高桩承台基础的抗震延性能力参数分析 [J]. 土木工程学报, 2018, 51(5): 112-121. (WANG Xiaowei, BLANCO G, YE Aijun, et al. Parametric study on seismic ductility capacity of bridge elevated pile-cap foundation in sand[J]. China Civil Engineering Journal, 2018, 51(5): 112-121. (in Chinese)) ↩
MCKENNA F. OpenSees: A framework for earthquake engineering simulation[J]. Computing in Science and Engineering, 2011, 13(4): 58-66. ↩
MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826. ↩
WANG X, SHAFIEEZADEH A, YE A. Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground[J]. Bulletin of Earthquake Engineering, 2018, 16(1): 229-257. ↩
ZHANG Y, CONTE J P, YANG Z, et al. Two-dimensional nonlinear earthquake response analysis of a bridge-foundation-ground system[J]. Earthquake Spectra, 2008, 24(2): 343-386. ↩
赫中营, 叶爱君. 力法非线性梁柱单元的合理单元长度划分 [J]. 工程力学, 2014, 31(7): 178-184. (HE Zhongying, YE Aijun. Reasonable discrete element length of force-based nonlinear beam-column elements[J]. Engineering Mechanics, 2014, 31(7): 178-184. (in Chinese)) ↩
WANG X, YE A, JI B. Fragility-based sensitivity analysis on the seismic performance of pile-group-supported bridges in liquefiable ground undergoing scour potentials[J]. Engineering Structures, 2019, 198: 109427. ↩ ↩
API. Geotechnical and foundation design considerations[S]. Washington D.C.: American Petroleum Institute, 2011. ↩ ↩ ↩
O'NEILL M W, MURCHISON J M. An evaluation of py relationships in sands[M]. Houston, TX: University of Houston, 1983. ↩
MOSHER R L. Load transfer criteria for numerical analysis of axial loaded piles in sand[R]. WES-TR-K-84-1. Vicksburg, MS: Automatic Data Processing Center, 1984. ↩ ↩
KULHAWY. Drilled shaft foundation[M]//H. Y. FANG. Foundation Engineering Handbook. 2nd Edition. New York: Van Nostrand Reinhold, 1991. ↩
MEYERHOF G. Bearing capacity and settlement of pile foundations[J]. Journal of the Geotechnical Engineering Division, 1976, 102(3): 195-228. ↩ ↩ ↩
WILSON D W. Soil-pile-superstructure interaction in liquefying sand [D]. Davis, CA: University of California, Davis, 1998. ↩
BAKER J W, LIN T, SHAHI S K, et al. New ground motion selection procedures and selected motions for the PEER transportation research program[R]. PEER Report 2011-03, Berkeley, CA: Pacific Earthquake Engineering Research Center, 2011. ↩
AHMED B F, DASGUPTA K. Seismic limit states for reinforced concrete bridge pile in sand[J]. Structures, 2021, 33: 128-140. ↩