吴学平,李闯,叶爱君(1. 同济大学土木工程防灾国家重点实验室,上海市 200092;2. 浙江数智交院科技股份有限公司,浙江杭州 310013)
摘要:中小跨度斜交连续梁桥普遍采用板式橡胶支座,在地震作用下,主梁与支座间容易发生滑动,同时主梁会发生平面内转动,落梁风险较大。以中等烈度区一座三跨斜交连续矮 T 梁桥为工程背景,建立板式橡胶支座支承的斜交桥有限元模型,采用非线性时程分析方法,进行地震反应特性分析,针对性地提出了板式橡胶支座(允许滑动)+ 钢阻尼器的组合减震体系,并对提出的减震体系做了位移控制效果分析。结果表明:在地震作用下,斜交桥中板式橡胶支座极易发生滑动,从而增大主梁地震位移并丧失自复位能力,但只要不发生主梁与桥台(挡块)的碰撞,主梁平面内转动的影响可以忽略不计。板式橡胶支座 + 钢阻尼器的组合减震体系可以有效控制主梁纵横向位移,并限制主梁平面内转动。
关键词:斜交桥板式橡胶支座矮 T 梁抗震体系钢阻尼器
中图分类号:U443.2 文献标志码:A 文章编号:1009- 7716(2022)06- 0219- 05
0 引言
斜交桥在高速公路和城市道路中较为常见。中小跨度斜交连续梁桥通常采用普通板式橡胶支座,由于斜交角的存在,斜交桥锐角侧恒载支反力小于对应直桥恒载支反力,在相同的地震动输入下,斜交桥比对应直桥更容易产生板式支座的滑动。在汶川地震中,板式橡胶支座桥梁由于支座滑动导致的桥梁移位震害非常常见,而斜交桥中支座滑动还会使主梁发生平面内转动,因此主梁移位震害更为严重。图 1 是汶川地震中一座多跨简支斜桥主梁平面内转动后的主梁移位震害,主梁产生平面转动后,锐角侧撞击横向挡块,钝角侧撞击桥台或相邻主梁,加剧主梁平面内旋转,增大落梁风险。因此,有必要研究斜交连续梁桥的合理抗震体系,解决其在地震中普通板式橡胶支座滑动后导致结构缺乏回复力,地震位移难以估计的问题。

图 1 斜交桥主梁移位震害
目前,斜交桥的抗震研究多集中于地震时普遍发生的主梁平面内旋转现象的产生机制和地震反应的数值建模方法。Maleki 对跨度为10\sim 30\mathrm{m}斜度为0^{\circ}\sim 60^{\circ}的简支斜交桥进行了地震反应分析和计算模型的比较。Kelley 研究了斜交桥的简化建模方法,并比较了不同简化方法的计算结果。何健等研究了斜交连续梁桥的有限元简化建模方法,提出了一种带碰撞单元并考虑竖向、水平和扭转刚度的单梁简化模型。Meng 等以斜度、刚度偏心率、宽跨比等作为基本参数进行了地震反应特征影响的分析。卓秋林对公路简支斜交桥在支座刚度、多跨简支结构等方面做了相关研究。以上研究主要关注斜交桥的有限元模型和地震反应特性的参数分析。研究结果表明,墩(台)梁间的碰撞使斜交桥产生主梁平面内转动,但几乎没有针对抗震体系进行相关研究。
为了研究斜交连续梁桥的合理抗震体系,本文选取中等烈度区一座三跨连续斜交梁桥为工程背景,建立板式橡胶支座支承斜交桥的非线性动力有限元模型,进行时程反应分析,重点研究常规体系下板式支座的滑动情况和主梁平面转动问题。然后提出板式橡胶支座 + 钢阻尼器的组合减震体系,并分析这一体系对主梁位移的控制效果。
1 背景工程与动力分析模型
本文以一座3\times 16\mathrm{m}连续斜交梁桥为工程背景,其平面图如图 2 所示。各墩、台编号从左至右分别为 0 号桥台、1 号墩、2 号墩、3 号桥台。其中,全局坐标系\mathcal{X}轴为桥轴纵向,\mathcal{Y}轴为桥轴横向,局部坐标系\mathcal{X}_1轴为与桥轴纵向夹-55^{\circ}角方向,\mathcal{Y}_1轴为与桥轴纵向夹35^{\circ}角方向。该桥斜交角为35^{\circ},属于大斜交角桥梁。上部结构采用 7 片预制矮 T 梁拼装,梁高0.8\mathrm{m},单幅宽10.5\mathrm{m},每片矮 T 梁梁端设置 1 个普通板式橡胶支座。其中,桥台处采用\mathrm{GYZF}_4350\times 65型四氟滑板橡胶支座,桥墩采用\mathrm{GYZ350\times 63}型普通板式橡胶支座。桩柱式桥墩横桥向为双柱框架结构,墩柱土上部分长度分别为2.2\mathrm{m}和3.4\mathrm{m};土下部分长度分别为65.974\mathrm{m}和65~\mathrm{m}。桩柱式墩采用圆形截面,土上部分直径为1.1\mathrm{m};土下部分直径为1.2\mathrm{m}。
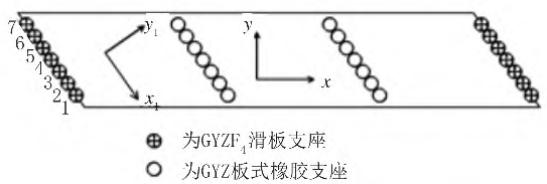
图 2 桥梁平面布置图
本文基于 SAP2000 软件建立了桥梁的空间有限元动力分析模型,如图 3 所示。模型中,主梁、桩柱、柱顶盖梁均用弹性梁单元模拟。盖梁节点用刚臂连接,质量集中于质心。支座采用连接单元模拟。根据《公路桥梁抗震设计规范》9,普通板式橡胶支座采用如图 4(a)所示的线弹性本构模型,刚度为2564~\mathrm{kN/m},水平位移能力为0.045\mathrm{m}(剪切应变允许值100\%),支座顶橡胶与钢板动摩擦系数为 0.2,对应支座滑动位移0.041\mathrm{m}。因此,地震时板式橡胶支座将在达到设计位移前发生滑动,而考虑支座滑动后的普通板式橡胶支座和四氟滑板橡胶支座(摩擦系数0.02)采用理想弹塑性本构模型,如图 4(b)所示。桩-土相互作用采用沿桩身分布的土弹簧模拟,土弹簧刚度按《公路桥涵地基与基础规范》10中的“m 法”计算,桩尖固接处理。
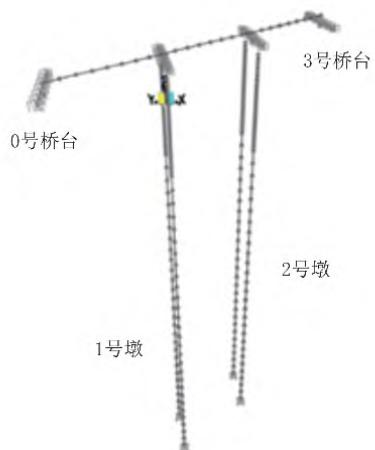
图 3 桥梁动力分析模型
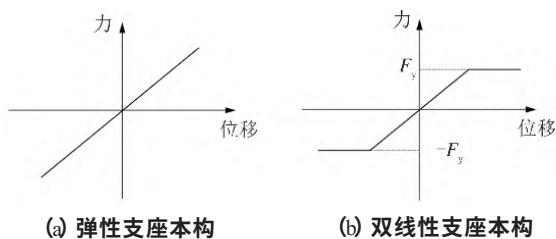
图 4 支座本构模型
2 地震动输入与桥梁动力特性
根据《公路桥梁抗震设计规范》9,场地水平向设计反应谱按式(1)式(2)确定。
其中,反应谱水平段起点T_{0} = 0.1\mathrm{s},特征周期T_{\mathrm{s}} = 0.65\mathrm{s},结构重要性系数C_i = 1.7,场地系数C_s = 1.2,阻尼调整系数C_d = 1,地表地震动加速度峰值A = 0.1g,反应谱峰值S_{\mathrm{max}} = 0.5\mathrm{g}。
以这一设计反应谱为目标,本文拟合了 7 条人工地震加速度时程。图 5 代表性地给出了其中一条人工加速度时程曲线,图 6 对人工加速度时程对应反应谱和设计反应谱进行了比较。结果表明,两者吻合程度较好。因此,本文采用上述 7 条人工加速度时程作为地震动输入,地震反应结果取 7 条地震动输入的平均值。
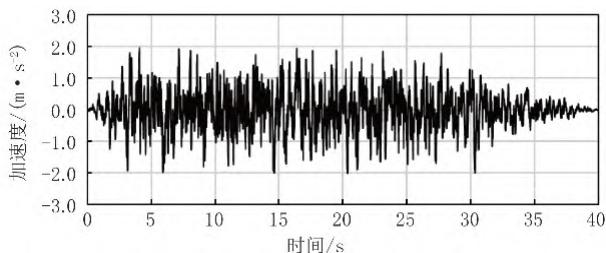
图 5 地震加速度时程
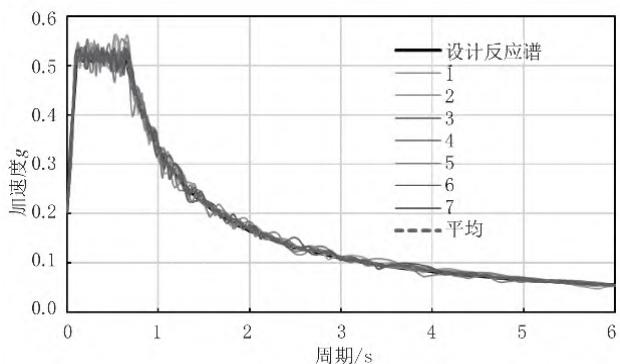
图 6 加速度时程对应反应谱与设计反应谱比较
表 1 列出了桥梁前 3 阶振型及对应的周期。从中可以看出斜交梁桥振型不同于一般直桥,出现了墩梁反对称横向振动。表明该桥的整体转动刚度相对其纵向、横向刚度要小。
表 1 桥梁动力特性
| 振型阶数 | 周期/s | 振型描述 |
|---|---|---|
| 1 | 2.14 | 墩梁反对称横向振动 |
| 2 | 1.72 | 墩梁纵向振动 |
| 3 | 1.31 | 墩梁横向振动 |
3 中小跨度常规体系斜交连续梁桥地震位移响应
首先不考虑普通板式支座的滑动,对常规体系桥梁进行了非线性时程分析。考虑到斜交连续梁桥地震反应的纵横向耦联性,分别考虑了纵桥向、横桥向、桥轴线35^{\circ}和桥轴线-55^{\circ}四个地震输入方向(分别对应图 2 中的x_{1}y_{1}y_{1}x_{1}四个方向)进行比较分析。表 2 列出了常规体系各输入方向下中墩板式橡胶支座、桥台四氟滑板支座的纵横向位移最大值和主梁平面内转角最大值。由表 2 可知:由于板式支座滑动位移仅0.041\mathrm{m},因此各工况下板式支座均出现滑动。纵向输入为支座纵向位移最不利工况,横向输入为支座横向最不利工况,35^{\circ}方向输入为主梁平面内转角最不利工况。
表 2 支座位移及主梁转角最大值
| 输入 方向 | 板式支座位移/m | 滑动支座位移/m | 主梁转角/ (×10-4rad) | ||
|---|---|---|---|---|---|
| 纵向 | 横向 | 纵向 | 横向 | ||
| 纵向 | 0.052 | 0.025 | 0.094 | 0.053 | 4.46 |
| 横向 | 0.026 | 0.056 | 0.050 | 0.088 | 5.91 |
| 35° | 0.044 | 0.030 | 0.090 | 0.064 | 6.41 |
| -55° | 0.039 | 0.056 | 0.050 | 0.075 | 2.79 |
进一步,为研究板式橡胶支座滑动对主梁平面内转动的影响,考虑板式橡胶支座的滑动(为避免程序求解时刚度矩阵奇异,板式支座滑动后刚度取10\mathrm{kN/m}),对常规体系桥梁进行了地震反应分析,地震输入方向为主梁平面内转角最不利的35^{\circ}方向。表 3 列出了常规体系考虑板式支座滑动与否的支座位移最大值。该工况下不考虑板式橡胶支座滑动时主梁平面转角为6.41\times 10^{-4}~\mathrm{rad},考虑板式橡胶支座滑动时主梁平面转角为9.79\times 10^{-4}~\mathrm{rad},增大52.7\%。结果表明:考虑板式支座滑动后,板式支座、四氟滑板支座位移最大值和主梁平面内转角最大值显著增大,主梁落梁与碰撞风险进一步提高。
为了分析支座滑动后,主梁平面转动对墩梁相对位移的影响,表 4 列出了 1 号墩顶横向 7 个板式支座、0 号桥台顶横向 7 个四氟滑板支座的位移分布。
表 3 支座位移最大值
| 分量 | 纵向 | 横向 | ||||
|---|---|---|---|---|---|---|
| 不考虑滑动 | 考虑滑动 | 增大率/% | 不考虑滑动 | 考虑滑动 | 增大率/% | |
| 板式支座位移/m | 0.044 | 0.052 | 18.2 | 0.030 | 0.037 | 23.3 |
| 滑动支座位移/m | 0.090 | 0.103 | 14.4 | 0.064 | 0.080 | 25.0 |
注:增大率=(考虑滑动响应 - 不考虑滑动响应)/ 不考虑滑动响应。
情况。由表 4 可知,桥台和桥墩上横向各支座的纵横向位移差别很小(最大仅差3.9\%)。因此,当主梁和桥台或挡块间不发生碰撞时,主梁平面转动的影响可以忽略不计。
表 4 墩台顶横向各支座位移
| 支座编号 | 板式支座位移/m | 滑动支座位移/m | ||
|---|---|---|---|---|
| 纵向 | 横向 | 纵向 | 横向 | |
| 1 | 0.051 5 | 0.035 8 | 0.101 3 | 0.077 0 |
| 2 | 0.051 6 | 0.035 9 | 0.101 6 | 0.077 5 |
| 3 | 0.051 7 | 0.036 1 | 0.101 9 | 0.078 0 |
| 4 | 0.051 8 | 0.036 3 | 0.102 2 | 0.078 5 |
| 5 | 0.051 9 | 0.036 4 | 0.102 5 | 0.079 0 |
| 6 | 0.052 0 | 0.036 6 | 0.102 9 | 0.079 5 |
| 7 | 0.052 1 | 0.036 7 | 0.103 2 | 0.080 0 |
| 最大支幅/% | 1.2 | 2.5 | 1.9 | 3.9 |
注:最大变幅=(最大响应 - 最小响应)/ 最小响应
4 中小跨度斜交连续梁桥合理抗震体系
由前述分析可知,在地震作用下,常规体系中小跨度斜交连续梁桥中板式橡胶支座极易发生滑动,从而增大支座地震位移,并增大主梁与桥台或挡块间的碰撞风险,而碰撞又会加剧主梁的平面转动11,进而增大落梁风险。反之,只要避免主梁与桥台或挡块间发生碰撞,地震中主梁的平面转动就可以忽略。因此,对于中小跨度斜交梁桥,合理的抗震对策是采取合理抗震体系,控制普通板式橡胶支座滑动后的主梁位移,并避免主梁与桥台或挡块间发生碰撞。
4.1板式橡胶支座+钢阻尼器组合减震体系
基于前述分析,本文提出采用普通板式橡胶支座(考虑滑动)与钢阻尼器组合的减震体系。其中,板式支座承担结构的竖向荷载,滑动后延长结构周期并通过摩擦提供一定的耗能能力,钢阻尼器在耗能的同时提供复位能力,限制主梁的位移。另外,中小跨度斜桥墩顶空间有限,不仅要求钢阻尼器构造简单、受力明确,还要求尺寸小。因此,本文选用沈星等12研发的以三角形钢板作为基本耗能构件的桥梁钢阻尼器。该阻尼器可以在横向(纵向)耗能的同时适应主梁的纵向(横向)变形。
桥梁横向钢阻尼器如图 7(a)所示,其力学本构可采用如图 7(b)所示的双线性本构模型。
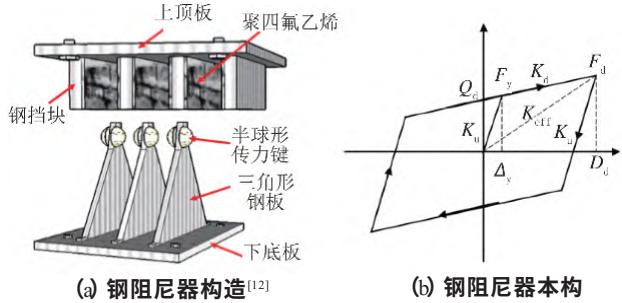
图 7 钢阻尼器构造及力学本构
根据已有研究成果13,结合桥梁的结构特点和常规体系的地震反应特性,为了不影响桥梁的正常使用功能,本文在桥梁 1 号墩墩顶设置 1 个纵向钢阻尼器,在 1 号墩、2 号墩墩顶各设置 1 个横向钢阻尼器。
1 号墩上钢阻尼器布置形式如图 8 所示,经过优化计算,综合考虑下部结构的地震内力和主梁位移,确定了钢阻尼器的选型:单个钢阻尼器含 3 块三角形钢板,其高、宽、厚分别为25\mathrm{cm}、37.5\mathrm{cm}、2\mathrm{cm}。板材为 Q345,总屈服力为138~\mathrm{kN},弹性总刚度为19680~\mathrm{kN/m},屈后硬化率为0.071。
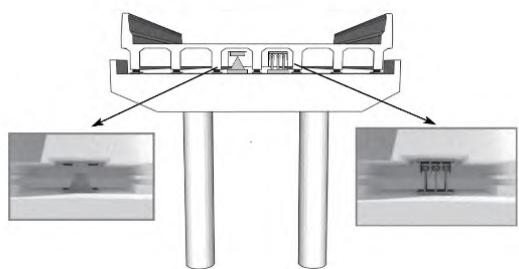
图 8 钢阻尼器布置示意图
4.2组合减震体系位移控制效果分析
为了说明这一组合减震体系中钢阻尼器对桥梁位移的控制效果,本文采用前述 7 条地震加速度时程,按最不利方向输入,进行了非线性时程反应分析,分别得到支座的纵向最大位移、横向最大位移和主梁最大转角的平均值,并与常规体系进行了比较,结果见表 5。结果表明,钢阻尼器使板式支座、滑动支座纵向位移分别减小了30.3\%、15.7\%,横向位移分别减小了45.3\%、38.5\%,而主梁转角更是减小了57.7\%,可见能有效控制桥梁位移。
进一步,本文选取其中一条地震加速度时程,代表性地给出了常规体系和组合减震体系桥梁的关键位移反应时程曲线。图 9、图 10 分别给出了纵向、横向输入下 0 号桥台四氟滑板支座的纵向、横向位移。
表 5 两种体系桥梁位移、转角比较
| 输入方向 | 反应分量 | 常规体系 | 组合减震体系 | 减震率/% |
|---|---|---|---|---|
| 纵向 | 板式支座位移/m | 0.066 | 0.046 | 30.3 |
| 滑动支座位移/m | 0.108 | 0.091 | 15.7 | |
| 横向 | 板式支座位移/m | 0.075 | 0.041 | 45.3 |
| 滑动支座位移/m | 0.109 | 0.067 | 38.5 | |
| 35° | 主梁转角/(×10-4rad) | 9.79 | 4.14 | 57.7 |
注:减震率 = (常规体系响应 - 减震体系响应)/ 常规体系响应。时程曲线,图 11 对35^{\circ}方向输入下两种体系主梁的平面转角时程进行了对比。结果同样表明,钢阻尼器能有效控制支座的位移和主梁的平面转动。
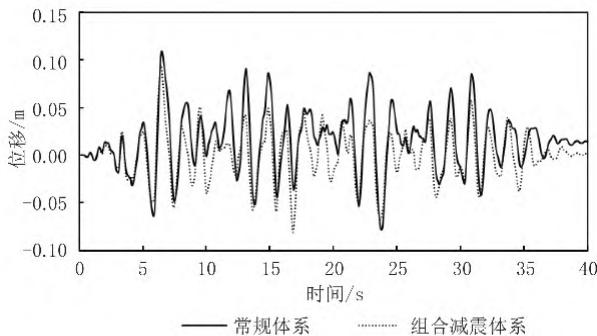
图 9 滑动支座纵向位移
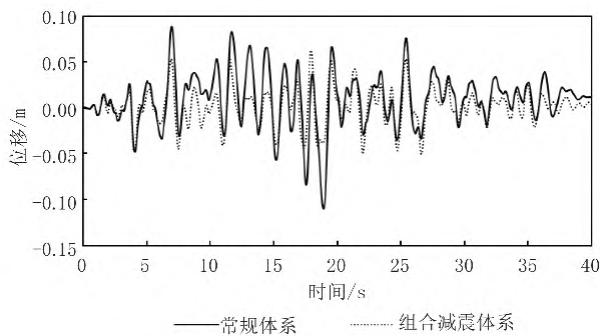
图 10 滑动支座横向位移
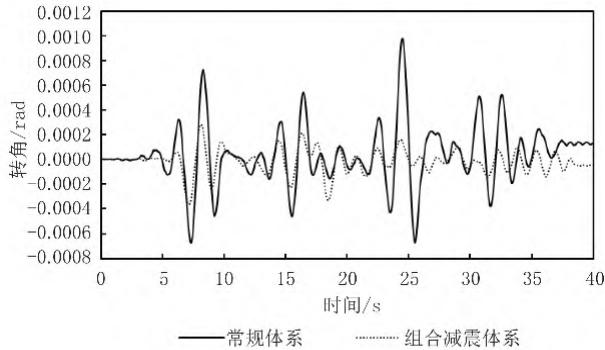
图 11 主梁平面转角
5 结语
本文以一座三跨斜交连续矮 T 梁桥为工程背景,通过动力特性分析和非线性时程分析,分析了常规体系桥梁的地震反应特性。然后针对常规体系存在的问题提出了一种组合减震体系,并进行了减震效果分析。结果表明:
(1) 地震作用下,板式橡胶支座支承的中小跨度斜桥极易发生支座滑动,从而使桥梁丧失自复位能力,显著增大主梁、墩(台)间相对位移和碰撞风险。
(2) 对于斜桥,只要不发生主梁与桥台(挡块)的碰撞,主梁平面内转动的影响可以忽略不计。
(3) 对于中等烈度区的中小跨度斜桥,板式橡胶支座(允许滑动)+ 钢阻尼器的组合减震体系可有效控制主梁纵横向位移,并限制主梁平面转动。
参考文献
黄平明. 混凝土斜交桥 [M]. 北京:人民交通出版社,1999.
项海帆. 高等桥梁结构理论 [M]. 北京:人民交通出版社,2013.
庄卫林,刘振宇,蒋劲松. 汶川大地震公路桥梁震害分析及对策 [J]. 岩石力学与工程学报,2009,28(7):1377- 1378.
Maleki S. Deck modeling for seismic analysis of skewed slab- girder bridges[J]. Engineering Structures,2002,24(10):1315- 1326.
Kelley J D. Three dimensional finite element modeling techniques and their effect on the seismic response of a highly skewed mul- ti- span bridge[D]. Philadelphia: Drexel University. College of Engineering,2005:1- 20.
何健,叶爱君. 连续斜交梁桥地震下碰撞效应分析 [J]. 中南大学学报(自然科学版),2012,43(4):1475- 1481.
Meng J Y, Lui E M. Reduced stick model for dynamic analysis of skew highway bridges[J]. Journal of Bridge Engineering,2002,7(3):184- 194.
卓秋林. 公路简支斜梁桥地震反应分析 [D]. 福州:福州大学土木工程学院,2004:5- 30.
JTG D63—2007,公路桥涵地基与基础规范 [S]. ↩
王军文,湛敏,邓琴,等. 三跨斜交简支梁桥地震旋转机理及斜度影响研究 [J]. 哈尔滨工程大学学报,2018,39(8):1357- 1362. ↩
沈星,倪晓博,叶爱君. 桥梁新型横向金属阻尼器研究 [J]. 振动与冲击,2014,33(2):96- 101. ↩
叶爱君,等. 小箱梁桥横向减震体系及其耗能特性 [J]. 中国公路学报,2017,30(12):22- 29. ↩