刘延芳,叶爱君,王斌斌 (同济大学桥梁工程系,上海 200092)
[摘要] 本文以苏通大桥南引桥为例,按照现行《公路工程抗震设计规范》提供的相关计算公式与有限元的计算结果进行比较分析,探讨了梁桥纵横向相邻桥跨之间的耦联作用。比较结果表明:对于纵桥向,两者反应谱的计算结果相差不大。时程结果表明,如果不考虑滑动摩擦支座的滞回耗能作用,两者的计算结果误差较大;对于横桥向,非均匀刚度的连续梁桥相邻跨之间的耦联性较大,建议今后采用规范对于明显非均匀刚度连续梁桥的横桥向进行地震反应分析时应该予以重视。
[关键词] 桥梁;抗震设计规范;非均匀刚度;耦联作用
[中图分类号] U448.21*5 [文献标识码] A
Applicability of the Existing Seismic Design Code for the Ultra Long Multispan Continuous Bridges
Liu Yan-fang, Ye Ai-jun, Wang Bin-bin (Department of Bridge Engineering, Tongji University, Shanghai 200092, China)
Abstract: Taking the south approach of the SUTONG Bridge as example, the interaction of the adjacent spans in the longitudinal and lateral direction is discussed in this paper, comparing the results according to Specifications of Earthquake Resistant Design for Highway Engineering with the results from FEM analysis. The results indicate that in longitudinal direction the results of the two methods are almost the same based on response spectrum analysis, but the discrepancy of the two methods through time-history analysis are consequent when the ability of energy dissipated of friction bearing is not taken into account. Meanwhile, in lateral direction, much more attention should be paid to the seismic analysis of the inhomogeneous rigidity's continuous bridges due to the remarkable interaction between the adjacent spans.
Keywords: bridges; seismic design code; Inhomogeneous rigidity; couple
1 概述
目前,大型桥梁工程的引桥往往采用连续梁桥的结构形式,且单联的桥跨数有不断增多的趋势。如东海大桥的引桥采用的结构形式主要是 5 \times 30\mathrm{m} 、 7 \times 50\mathrm{m}, 6 \times 60\mathrm{m}, 5 \times 70\mathrm{m} 的预应力混凝土连续梁桥,而苏通大桥引桥采用的结构形式主要是 12 \times 30\mathrm{m} , 11 \times 50\mathrm{m}, 10 \times 75\mathrm{m} 的预应力混凝土连续梁桥,单联跨数均超过 10 跨,最长一联长度达 750\mathrm{m} 。由于现行《公路工程抗震设计规范》(以下简称《规范》)适用于主跨不超过 150\mathrm{m} 的梁桥和拱桥,但没有明确规定适用的桥梁长度,因此工程师们大多认为这些连续梁桥是常规结构,可以参照现行《规范》进行抗震设计。实际上,盲目地采用《规范》提供的公式进行
地震反应计算可能会导致不安全的后果。而且,在历次破坏性地震中,梁桥的破坏最为严重。因此,有必要对超长多跨连续梁桥的地震反应分析进行研究。
本文以苏通大桥南引桥为例,将按现行《规范》提供的相关计算公式与有限元的计算结果进行比较分析,研究现行《规范》对于超长多跨连续梁桥的地震反应分析的适用性,并且探讨梁桥的纵横向相邻桥跨之间的耦联作用。
2 计算模型及地震动输入
苏通大桥南引桥为三联的连续梁桥,跨径布置为 11 \times 50\mathrm{m} (第一联) +11 \times 50\mathrm{m} (第二联) +11 \times 50\mathrm{m} (第三联),全长 1650\mathrm{m} 。墩号从 80 \sim 113 ,墩顶标高从 50.387\mathrm{m} 变化到 16.316\mathrm{m} 。其中 84 \sim 87,95 \sim 98,107 \sim 108 号墩采用固定支座,其余各墩均采用滑动支座。南引桥方案设计为双幅桥,两幅主梁之间无
横向连接,本文采用单幅桥建模。
有限元的动力分析采用三维模型,见图 1,其中,主梁、墩采用梁单元模拟;桩基础采用 6 根弹簧模拟。详细信息可参见文献4。

图 1 全桥动力模型
地震输入采用江苏省地震工程研究院提交的 500 年重现期的反应谱 (见图 2) 及对应的 6 组地震加速度时程,本文有选择地画了一组地震加速度时程,如图 3 所示。
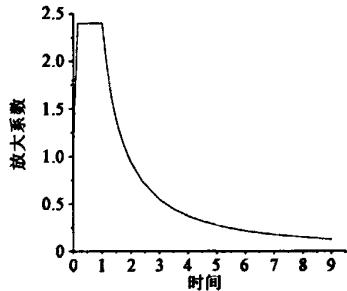
图 2500 年重现期水平向反应谱图
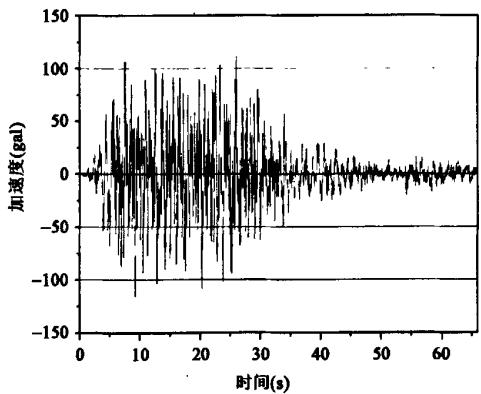
图 3500 年重现期水平向地表加速度时程
3 纵桥向地震反应分析比较
3.1 动力特性的比较分析
连续梁桥纵桥向基本周期的计算公式采用《规范》中附录一的计算公式,即将上部结构、盖梁、墩身的重力全部集中在支座顶面或上部结构的质量重心处按单质点体系进行计算,基本周期的计算公式为:
其中, G_\mathrm{t} 为单质点体系的总重力, \pmb{g} 为重力加速度, \delta 为在顺桥向或横桥向作用于支座顶面或上部结构
质量重心处单位水平力在该点引起的水平位移。
根据上述计算公式,计算得到苏通大桥南引桥三联连续梁桥的纵向基本周期,以及有限元模型的计算结果见表 1,可见两者吻合得很好,最大误差仅为 4.4\% 。
表 1 纵桥向各联基本周期 (s)
| 位置 | 规范结果 | 有限元结果 | 误差 |
|---|---|---|---|
| 第一联 | 5.64 | 5.9 | 4.4% |
| 第二联 | 3.6 | 3.7 | 2.7% |
| 第三联 | 2.93 | 3.0 | 2.3% |
3.2 反应谱分析结果比较
由于反应谱方法不能考虑支座的非线性,因此采用有限元模型进行反应谱分析时,一般忽略滑动支座的作用,即桥墩和梁相互自由。本文采用有限元模型进行纵桥向地震反应谱分析时,计算了前 300 阶振型,振型组合采用 CQC 方法。
出于结果的可比性考虑,相应地,采用规范公式进行地震反应分析时,也忽略滑动支座的作用,同时不考虑 C_{\mathrm{z}} 系数折减,即《规范》(4.2.6-4) 公式变化为:
式中, E_{\mathrm{hop}} 为单质点体系的总水平地震力,当有几个桥墩共同分担时,应按各桥墩的抗推刚度分配每桥墩顶面的水平地震力; K_{\mathrm{h}} 为水平地震系数; \beta 为相应于桥墩顺桥向基本周期的动力放大系数,根据输人反应谱计算。
根据上述计算原则,计算得到苏通大桥南引桥三联连续梁桥各固定墩底的地震内力,以及有限元模型的计算结果分别列于表 2,可见两者吻合得很好,墩底弯矩最大误差仅为 2.9\% 。
3.3 时程分析结果比较
采用有限元模型进行地震时程反应分析时,可以模拟滑动支座的滞回耗能作用。本文采用图 1 所示计算模型,考虑了滑动支座的摩擦耗能作用。
现行《规范》对于桥梁在地震作用下顺桥向地震作用的计算采用的是单墩的简化模型,对于滑动支座,现行规范仅考虑了各滑动摩擦力分担的上部结构惯性力,但没有考虑滑动摩擦支座的动力滞回耗能作用。出于结果的可比性考虑,采用《规范》(4.2.6-4) 公式进行地震反应分析时,不考虑 C_{\mathrm{z}} 系
数折减,则该公式变化为:
式中, E_{\mathrm{hop}} 为单质点体系的总水平地震力,当有几个桥墩共同分担时,应按各桥墩的抗推刚度分配每桥墩顶面的水平地震力; K_{\mathrm{h}} 为水平地震系数; \beta 为相应于桥墩顺桥向基本周期的动力放大系数,根据输入反应谱计算。 \mu_{\mathrm{id}} 为第 i 号聚四氟乙烯滑板支座的动摩阻系数,取 \mu_{\mathrm{id}} = 0.02;R_{i} 为上部结构重力在第 i 号聚四氟乙烯滑板支座上产生的反力 (kN)。
根据上述计算原则,计算得到苏通大桥南引桥三联连续梁桥各固定墩底的地震内力,以及有限元模型的计算结果分别列于表 3,可见规范公式的计算结果与有限元的时程分析结果相比偏于保守,并且随着桥墩高度的降低,即桥墩刚度的增加,两者的差别也随之增加,误差为 35.6\% \sim 79.4\% 。两者之间较大的误差,主要是由于规范公式没有考虑滑动摩擦支座的滞回耗能作用,可见滑动摩擦支座的滞回耗能作用非常显著。
表 2 各固定墩纵桥向地震内力比较 (反应谱法)
| 联号 | 墩号 | 分配水平力 | 墩底弯矩 | 墩底剪力 | 墩底弯矩 | 弯矩误差(%) |
|---|---|---|---|---|---|---|
| 第一联 | 84 | 1.16E+03 | 5.09E+04 | 1.45E+03 | 5.09E+04 | 0 |
| 85 | 1.17E+03 | 5.02E+04 | 1.34E+03 | 5.09E+04 | 1.4 | |
| 86 | 1.35E+03 | 5.50E+04 | 1.61E+03 | 5.55E+04 | 1.0 | |
| 87 | 1.50E+03 | 5.84E+04 | 1.72E+03 | 5.88E+04 | 0.7 | |
| 第二联 | 95 | 2.05E+03 | 6.31E+04 | 2.17E+03 | 6.24E+04 | 1.1 |
| 96 | 2.28E+03 | 6.71E+04 | 2.38E+03 | 6.66E+04 | 0.8 | |
| 97 | 2.54E+03 | 7.16E+04 | 2.60E+03 | 7.09E+04 | 1.0 | |
| 98 | 2.82E+03 | 7.61E+04 | 2.85E+03 | 7.48E+04 | 1.7 | |
| 第三联 | 107 | 5.70E+03 | 9.64E+04 | 5.89E+03 | 9.90E+04 | 2.6 |
| 108 | 6.19E+03 | 1.01E+05 | 6.39E+03 | 1.04E+05 | 2.9 |
表 3 各固定墩纵桥向地震内力比较 (时程法)
| 联号 | 墩号 | 分配水平力 | 墩底弯矩 | 墩底剪力 | 墩底弯矩 | 弯矩误差(%) |
|---|---|---|---|---|---|---|
| 第一联 | 84 | 8.42E+02 | 3.62E+04 | 8.39E+02 | 2.67E+04 | 35.6 |
| 85 | 8.44E+02 | 3.63E+04 | 8.43E+02 | 2.67E+04 | 36.0 | |
| 86 | 9.80E+02 | 3.98E+04 | 9.06E+02 | 2.92E+04 | 36.3 | |
| 87 | 1.08E+03 | 4.22E+04 | 9.65E+02 | 3.10E+04 | 36.1 | |
| 第二联 | 95 | 1.75E+03 | 5.37E+04 | 1.11E+03 | 3.17E+04 | 69.4 |
| 96 | 1.94E+03 | 5.72E+04 | 1.21E+03 | 3.39E+04 | 68.7 | |
| 97 | 2.16E+03 | 6.10E+04 | 1.33E+03 | 3.61E+04 | 69.0 | |
| 98 | 2.40E+03 | 6.48E+04 | 1.46E+03 | 3.80E+04 | 70.5 | |
| 第三联 | 107 | 4.87E+03 | 8.23E+04 | 2.70E+03 | 4.60E+04 | 78.9 |
| 108 | 5.29E+03 | 8.61E+04 | 2.93E+03 | 4.80E+04 | 79.4 |
4 横桥向地震反应分析
连续梁桥横桥向的振型受相邻结构的耦联性影响较大,整体模型与单墩模型的动力特性很难进行比较,所以本文不进行横桥向动力特性的比较,只进行横桥向地震反应分析的比较。
4.1 规范公式与整体有限元计算结果的比较
现行《规范》在计算连续梁桥的横桥向动力特性及地震反应时采用的依然是单墩的简化模型,近似认为一阶振型起控制作用,略去高阶振型的影响。
现行《规范》4.2.2 条规定,梁桥桥墩顺桥向和横桥向的水平地震荷载,一般情况下应按下式计算:
式中, E_{i\mathrm{hp}} 为作用于梁桥桥墩各质点 i 的水平地震荷载; C_i, C_\mathrm{z}, K_\mathrm{h} 分别为重要性修正系数、综合影响系数和水平地震系数; \beta 为相应于桥墩横桥向基本周期的动力放大系数,基本周期根据规范公式计算; \gamma_1 为桥墩横桥向的基本振型参与系数。
X_{1i} 为桥墩基本振型在 i 分段重心处的相对水平位移,根据《规范》公式计算; G_{i = 0} 为梁桥上部结构重力,计算横桥向地震荷载时为相邻两孔梁重力的一半; G_{i = 1,2,3,\dots} 为桥墩墩身各分段的重力。
本文以非均匀刚度连续梁桥 - 苏通桥南引桥为例,对规范公式的适用性进行了分析。表 4 对规范公式的计算结果和连续梁桥整体有限元模型的计算结果进行了比较,结果表明,对于非均匀刚度的连续梁桥,采用单墩模型的现行规范公式的计算结果对于高墩明显偏小,而对于矮墩则显著偏大。就弯矩来说,每一联弯矩的误差随着墩高的降低逐渐增大。总体来说,矮墩误差比高墩大,弯矩误差比剪力大。
表 4 规范结果与整体有限元结果比较
| 截面位置 | 分配水平力 | 墩底弯矩 | 墩底剪力 | 墩底弯矩 | 剪力 | 弯矩 |
|---|---|---|---|---|---|---|
| 第一联 | ||||||
| 81#墩底 | 1.95E+03 | 9.06E+04 | 2.60E+03 | 9.59E+04 | -25.0 | -5.5 |
| 85#墩底 | 2.06E+03 | 8.63E+04 | 3.12E+03 | 1.14E+05 | -34.0 | -24.3 |
| 89#墩底 | 2.40E+03 | 9.09E+04 | 2.39E+03 | 7.49E+04 | 0.4 | 21.4 |
| 第二联 | ||||||
| 92#墩底 | 2.94E+03 | 9.74E+04 | 2.99E+03 | 8.93E+04 | -1.7 | 9.1 |
| 96#墩底 | 3.51E+03 | 1.04E+05 | 3.42E+03 | 8.98E+04 | 2.6 | 15.8 |
| 100#墩底 | 4.38E+03 | 1.10E+05 | 3.79E+03 | 8.39E+04 | 15.6 | 31.1 |
| 第三联 | ||||||
| 103#墩底 | 5.20E+03 | 1.15E+05 | 4.06E+03 | 8.14E+04 | 28.1 | 41.3 |
| 107#墩底 | 5.30E+03 | 9.59E+04 | 4.10E+03 | 6.66E+04 | 29.3 | 44.0 |
| 111#墩底 | 5.22E+03 | 8.21E+04 | 3.29E+03 | 4.64E+04 | 58.7 | 76.9 |
4.2 误差来源的探讨
针对上述比较结果,为了探讨其误差来源,首先将规范公式的计算结果与单墩有限元的计算结果进行比较。
采用上述规范公式(不考虑重要性系数和综合影响系数)和单墩有限元模型,对多个桥墩的地震反应进行计算并列于表 5 做了比较。
表 5 结果表明,两种算法的弯矩计算结果吻合得很好,误差均在 1\% 之内,而对于剪力,高墩的误
差较大,最大的为 13.2\% (误差原因是梁与墩的振动相互耦合在一起所致),但矮墩的误差较小,如 91# 墩为 3.1\% ,100# 墩为 0.2\% 。考虑到高墩为弯矩控制设计,因此可以认为,对于单墩模型,规范公式和有限元模型的计算结果一致。
其次,由于现行《规范》在没有考虑相邻桥跨之间的横向耦联性时,其横桥向地震力计算结果与单墩模型吻合得较好;因此,本文对均匀刚度连续梁桥(各桥墩刚度以及各桥跨均相等)的相邻联结构耦联
性进行了分析,连续梁桥的跨数假定从 2 跨变化为 20 跨,图 4 直观显示了对于跨数不同的连续梁桥,单墩模型与整体有限元模型相比的计算误差随跨数增大的变化规律。可见,对于各桥墩刚度以及各桥
跨均相等的连续梁桥,相邻联结构耦联性很小,而且随着跨数的增大,误差明显变小,三跨以上的连续梁桥,单墩模型的计算误差仅在 5\% 以内。
表 5 规范公式与单墩有限元计算结果比较
| 截面位置 | 分配水平力 | 墩底弯矩 | 墩底剪力 | 墩底弯矩 | 剪力 | 弯矩 |
|---|---|---|---|---|---|---|
| 83#墩底 | 2.10E+03 | 9.40E+04 | 2.42E+03 | 9.48E+04 | 13.2 | 0.8 |
| 85#墩底 | 2.06E+03 | 8.63E+04 | 2.29E+03 | 8.60E+04 | 10.0 | 1.0 |
| 91#墩底 | 2.84E+03 | 9.76E+04 | 2.93E+03 | 9.68E+04 | 3.1 | 0.8 |
| 100#墩底 | 4.38E+03 | 1.10E+05 | 4.37E+03 | 1.09E+05 | 0.2 | 0 |
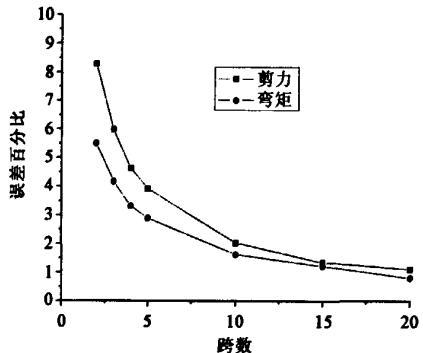
图 4 单墩模型误差随连续梁桥跨数的变化
由以上的误差分析结果可以看出,对于明显非均匀刚度的连续梁桥,现行《规范》公式与有限元对于横桥向计算结果的误差主要来自相邻桥跨之间的耦联作用。因此,按照现行《规范》公式对于明显非均匀刚度的连续梁桥在进行横桥向地震反应分析时是存在缺陷的。为此建议,今后在采用规范公式计算连续梁桥的横向地震反应时要慎重,应充分认识到相邻跨桥梁结构间的耦联作用。
5 结论
本文以苏通大桥南引桥为例,将按现行《规范》提供的相关计算公式的计算结果与有限元的计算结果进行比较分析,探讨梁桥的纵横向相邻桥跨之间的耦联作用,结果表明:
(1) 在纵向地震荷载作用下,现行规范的纵向计算结果与有限元的计算结果吻合的较好。
(2) 纵桥向时程分析结果表明,规范计算结果与有限元的时程分析结果相比偏于保守,并且随着桥墩高度的降低,即桥墩刚度的增加,两者的差别也随之增加,误差为 35.6\% \sim 79.4\% 。可见,滑动摩擦支座的滞回耗能作用很显著。
(3) 对于均匀刚度的连续梁桥,其横桥向相邻联结构耦联性很小,而且随着跨数的增大,误差明显变小,三跨以上的连续梁桥,单墩模型的计算误差仅在 5\% 以内。
(4) 对于明显非均匀刚度的连续梁桥,由于现行《规范》公式没有考虑横桥向相邻联桥跨之间的耦联作用,导致计算结果存在误差。建议,今后在采用规范公式计算连续梁桥的横向地震反应时应慎重。
参考文献:
范立础. 桥梁抗震 [M]. 上海:同济大学出版社,1997
范立础,胡世德,叶爱君.大跨度桥梁抗震设计 [M]. 北京:人民交通出版社,2001
JTJ004-89, 公路工程抗震设计规范 [S]. 北京: 人民交通出版社, 1990
同济大学土木工程防灾国家重点实验室. 苏通长江公路大桥跨江大桥工程结构抗震性能分析研究最终报告(下册)[P]. 上海, 2004 ↩