沈星,叶爱君,王晓伟
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:在目前单柱墩延性能力研究的基础上,通过分析动轴力和塑性铰机制对双柱墩弹塑性位移能力的影响,得出双柱墩弹塑性位移能力简化计算方法,并对该简化计算方法进行误差分析。结果表明:双柱墩墩顶简化计算屈服位移较推倒 (Pushover) 分析的屈服位移略大;当双柱墩轴压比为 5\% \sim 20\% 、长细比为 5 \sim 10 时,简化计算破坏位移误差在 20\% 内,随着长细比的增加和轴压比的减小,简化计算墩顶破坏位移小于 Pushover 分析的破坏位移,因此该简化计算方法的结果是偏安全的。
关键词:双柱墩;动轴力;塑性铰机制;推倒(Pushover)分析;弹塑性位移能力
中图分类号:U442.5
文献标志码:A
Simplified Calculation Method of Elastic-plastic Displacement Capacity for Double-column Bent
SHEN Xing, YE Aijun, WANG Xiaowei
(State Key Laboratory for Disaster Reduction of Civil Engineering, Shanghai 200092, China)
Abstract: Based on the current research for ductility capacity of single-column pier, a simplified calculation method of elastic-plastic displacement capacity for double-column bent was obtained by analyzing the effects of dynamic axial force and plastic hinge mechanism on the elastic-plastic displacement capacity of double-column bent. With the proposed simplified calculation method of double-column bent, the obtained yield tip pier displacement was larger than that calculated by pushover analysis and the accuracy was within the acceptable range. When the axial compression ratio was within 5\% \sim 20\% and the slenderness ratio was within 5 \sim 10 , the calculated tip pier collapse displacement was within 20\% . With the increasing of the slenderness ratio and the decreasing of axial compression ratio, the tip pier collapse displacement by the proposed simplified calculation method was less than that by pushover, therefore, the proposed simplified calculation method was safe.
Key words: double-column bent; dynamic axial force; plastic hinge mechanism; pushover analysis; elastic-plastic displacement capacity
桥梁结构抗震设计方法从基于力的抗震设计方法转变到基于性能的抗震设计方法1,目前美国常用的 AASHTO 和 Caltrans 抗震设计标准中都明确体现了这一设计理念:将结构根据损伤程度的不同,定义不同的性能目标,然后根据桥梁结构的重要性选择不同概率水准作用下,桥梁结构应达到的预期性能目标,从而使桥梁结构在抗震设计中的安全性和经济性达到平衡。基于性能的抗震设计方法需要准确预测结构力与位移的关系,以此判定结构是否处于预期性能目标状态下。因此,如何正确计算结构体系的弹塑性位移能力对采用基于性能抗震设计方法的结构至关重要。
目前,对单柱墩塑性位移能力的计算普遍采用基于集中塑性铰原理的计算方法,因此确定合理的等效塑性铰长度是计算单柱墩塑性位移能力的关键。关于等效塑性铰长度经验公式的试验研究及其影响因素的理论研究相当广泛。Park 等2从理论上推导出两侧配筋混凝土梁屈服曲率和破坏曲率的计算公式以及配筋率对曲率延性的影响,得出提高箍筋配筋率可以提高核心混凝土极限抗压强度以及增加塑性铰长度的结论。Bayrak 等3和 Bae 等4分别对 56 组钢筋和 162 组钢筋进行单调递增压压试验,研究受压区钢筋屈曲对塑性铰长度的影响。Dhakal 等5分析结构在承受单调递增荷载和循环滞回荷载时对塑性铰发展的影响,以及根据对 25 个墩、37 个梁、36 道墙的试验研究给出屈服曲率和极限曲率的简化计算方法。Dowell 等6和 Hines 等7对奥克兰海湾桥等实际工程的空心桥墩进行试验研究,针对该墩柱截面得出比 Priestley1提出的等效塑性较长度更准确的计算公式。Bae 等8对五个足尺单柱墩模型进行循环递推加载,从截面层次和构件层次研究 P-Delta 效应对等效塑性较长度的影响。Berry 等9通过对 37 个大尺寸圆柱墩模型进行试验研究并利用概率统计对 Priestley1提出的等效塑性较长度公式进行修正。沈星等10通过数值计算方法分析不同刚度变化的柔性横系梁结构,揭示出柔性横系梁双柱墩的破坏机理和抗震性能。韦晓等11采用振动台试验和理论分析相结合的方法对单柱式和双柱式桥墩结构抗震性能进行相关探讨。
单柱墩等效塑性铰长度经验计算公式已经得到各国规范的认同,但是对于双柱墩,由于在地震荷载作用下,双柱墩会受到随水平地震荷载变化的动轴力,同时墩顶由于系梁刚度的变化而产生塑性铰,因此国内外桥梁抗震规范对双柱墩墩顶位移能力要求采用推倒 (Pushover) 分析方法求解。但 Pushover 分析方法对于桥梁工程设计人员而言,计算过程过于繁琐,因此提出双柱墩墩顶弹塑性位移能力简化计算方法,对于采用基于性能抗震设计方法的结构简化延性验算具有重要的工程实践意义。
本文基于单柱墩成熟的弹塑性位移能力研究方法,分析双柱墩中动轴力和塑性铰机制对双柱墩弹塑性位移能力的影响,提出双柱墩弹塑性位移能力简化计算方法,并进行误差分析,同时给出该方法对双柱墩结构的适用范围。
1 动轴力对双柱墩弹塑性位移能力的影响
双柱墩在水平地震荷载作用下,墩柱截面内会产生随水平地震力变化的动轴力。本文首先从构件层次上分析动轴力与水平推力的关系,然后从截面层次上分析动轴力对关键截面曲率的影响,从而进一步得出动轴力对弹塑性位移能力的影响
1.1 双柱墩动轴力与水平推力的关系
针对一般双柱墩受力图,运用力法得出墩柱受动轴力和弯矩与水平推力的关系,具体受力图见图 1。
在单位水平推力作用下,单个墩柱所受的轴力和弯矩分别为
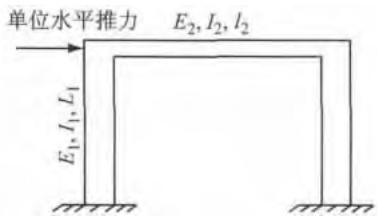
图 1 双柱墩受力图
Fig.1 Force diagram of double-column bent
式中: E_{1} 和 E_{2} 分别为墩和系梁的弹性模量, I_{1} 和 I_{2} 分别为墩和系梁的截面惯性矩, L_{1} 为双柱墩墩高, l_{2} 为系梁长度。根据公式可知:对于双墩柱结构,随着系梁刚度增大,墩柱产生的动轴力也越大。当系梁为柔性横系梁时,双柱墩墩柱内产生的动轴力很小,其墩柱受力图与单柱墩相近;当系梁为盖梁或刚性系梁时,即系梁的刚度很大,在双柱墩墩柱内产生的动轴力最大。
1.2 动轴力对双柱墩屈服位移的影响
双柱墩在屈服之前,结构的响应都在线性范围之内,即可在线性范围内分析动轴力对墩柱截面应力及等效刚度的影响,从而得到动轴力对双柱墩屈服位移的影响。
1.2.1 动轴力对墩柱截面应力的影响
当系梁刚度为无穷大时,双柱墩墩柱内产生的动轴力最大,动轴力对墩柱的影响也最大,因此仅以这一类刚性系梁双柱墩来进行分析。
当系梁刚度为无穷大时,动轴力与单位水平推力关系为
假定墩柱为矩形截面,边长为 a ,由动轴力在截面边缘产生的正应力
由弯矩在截面边缘产生的正应力
动轴力产生的正应力与弯矩产生的正应力之比为
假设系梁长度是墩柱截面边长的 5 倍时,动轴力在墩柱截面内产生的正应力为弯矩产生的正应力的 6.67\% 。可见动轴力对墩柱截面正应力的影响在 10\% 以内,对于柔性系梁双柱墩,动轴力对墩柱截面应力的影响将更小。
1.2.2 动轴力对墩柱截面等效刚度的影响
墩柱截面的等效刚度定义为截面首次屈服时的割线刚度。在水平地震荷载作用下,一侧墩柱承受动轴压力,使墩柱的刚度增加;另一侧墩柱则承受动轴拉力,使墩柱的刚度减小。考虑在一定范围内动轴力对刚度的影响是线性的,地震力在两个墩柱上产生的轴力相等,只是方向相反。
图 212 为不同纵向钢筋配筋率时,墩柱矩形截面承受不同轴压力所对应的开裂钢筋混凝土截面等效刚度的变化趋势。图中, A_{\mathrm{g}} 为混凝土截面面积,\mathrm{m}^2; A_{\mathrm{st}} 为截面纵筋总面积,\mathrm{m}^2; I_{\mathrm{e}} 为截面的等效惯性矩,\mathrm{m}^4; I_{\mathrm{g}} 为毛截面惯性矩,\mathrm{m}^4; f_{\mathrm{ck}} 为混凝土抗压强度标准值,\mathrm{kN} \cdot \mathrm{m}^2; F_{\mathrm{s}} 为截面所受到的轴力,\mathrm{kN} 。

图 2 开裂钢筋混凝土截面的等效刚度12
Fig.2 Effective stiffness of cracked reinforced concrete sections12
根据对双柱墩墩柱动轴力受力影响的分析和图 2 中墩柱截面随轴力变化对等效刚度敏感性分析可知,动轴力对双柱墩墩柱截面等效刚度影响很小,所以双柱墩的整体横向刚度与恒载作用下单柱墩的横向刚度变化不大,可以近似采用恒载作用下单柱墩墩底截面的等效刚度作为地震作用下的等效刚度。
以上分析可知,在线性范围内,动轴力对双柱墩墩柱截面内的屈服曲率影响很小,即在对双柱墩墩柱进行截面分析时,可以不考虑动轴力的影响,从而进行屈服位移能力的简化计算。
1.3 动轴力对双柱墩塑性位移的影响
结构进入屈服阶段以后,结构的动轴力由于核心混凝土的箍筋束缚效应和纵向钢筋的强化作用会有一定的增加,破坏时的动轴力也会比屈服时的动轴力大。但从数值分析的数据中得出,总的动轴力变化还是很小的。
墩柱关键截面屈服以后,截面外侧的正应力大小基本不变,截面内会发生应力重分布,截面内侧混凝土的正应力逐渐增大,整个截面的应变会不断增加。因此双柱墩的塑性位移能力取决于核心混凝土和纵向钢筋进入非线性后的本构关系,以及整个结构体系塑性铰机制对墩顶塑性位移的影响,而动轴力对关键截面破坏曲率相对于弯矩的影响是有限的。
2 塑性铰机制对双柱墩弹塑性位移能力的影响
单柱墩屈服后,仅在墩底形成一个塑性铰。对于双柱墩,当系梁的刚度很小时,墩底首先形成塑性铰,墩顶在破坏之前也不会屈服,即塑性铰机制与单柱墩类似。随着系梁刚度的增大,结构在屈服后不仅在墩底形成塑性铰,墩顶位置也将形成塑性铰。当为刚性系梁双柱墩时,墩底和墩顶屈服时将形成四个塑性铰。因此,可通过对单柱墩和刚性系梁双柱墩进行 Pushover 分析,分析比较两个结构体系墩顶力与位移的关系及弹塑性位移分布的关系。
2.1 有限元模型
本文基于 OpenSees 大型非线性有限元分析软件,利用其纤维面单元对单柱墩和刚性系梁双柱墩结构建立有限元模型,并进行 Pushover 分析,以此获得桥墩结构由开始受力经历屈服直至破坏倒塌时的弹塑性位移能力。
钢筋和混凝土本构关系对正确模拟结构进入塑性后的响应至关重要。本文有限元中本构模型参考文献10,13。双柱墩的屈服位移是以任一墩柱关键截面的钢筋达到屈服拉应变或核心混凝土外侧达到屈服压应变时的墩顶位移,破坏位移是以任一墩柱关键截面的钢筋达到极限拉应变被拉断或核心混凝土外侧达到极限压应变被压溃时的墩顶位移,塑性位移就是破坏位移和屈服位移之差。
2.2 双柱墩与单柱墩的力和位移关系比较
通过对单柱墩和刚性系梁双柱墩进行 Pushover 分析,得到两个结构体系从开始受力经历屈服直至最后破坏过程中墩顶水平推力与墩顶位移的关系曲线,以此来分析单柱墩与双柱墩结构体系总体刚度的区别。
双柱墩模型来源于实际工程,其钢筋配筋率均满足规范要求。 双柱墩墩柱采用矩形截面,截面尺寸为 1.8 \mathrm{~m} \times 1.8 \mathrm{~m} , 纵向钢筋配筋率为 2.509\% , 系梁长度为 12.5 \mathrm{~m} 。 墩柱采用纤维面单元; 系梁采用弹性单元, 并将其弹性模量设置得很大, 以此来模拟系梁的无穷大刚度。 单柱墩与双柱墩墩柱截面形式及尺寸相同, 通过模拟相同截面的单柱墩模型与刚性系梁双柱墩模型来探索双柱墩的弹塑性位移能力的变化规律。
由图 3 可知,刚性系梁双柱墩在屈服时的总体刚度是单柱墩在屈服时总体刚度的 8 倍。这是因为屈服时刚性系梁双柱墩在墩顶和墩底形成塑性铰,且墩顶和墩底产生的弯矩大小基本相同,方向相反。因此在总体结构上的响应表现为刚性系梁双柱墩承受的墩顶水平推力是单柱墩的 4 倍,而墩顶屈服位移却是单柱墩的一半。
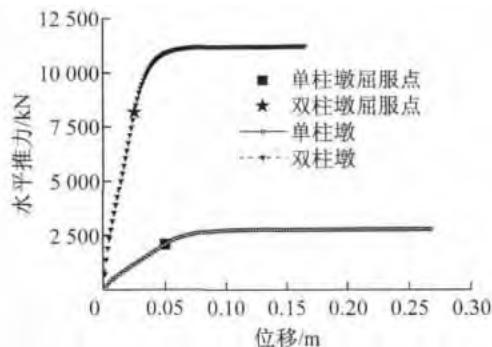
图 3 水平推力 - 位移关系对比
Fig.3 Comparison of lateral force-displacement relationship
2.3 双柱墩与单柱墩的弹塑性位移分布的比较
通过比较墩柱为 10\mathrm{m} 高的单柱墩和刚性系梁双柱墩在屈服阶段和破坏阶段的屈服位移分布和塑性位移分布,分析其弹塑性位移能力。由图 4 可知,刚性系梁双柱墩墩顶屈服位移是单柱墩的一半,而塑性位移可看成是绕墩底某一点的转动。即可以参照单柱墩,运用集中塑性铰方法来得到双柱墩的塑性位移。
由于动轴力对柔性系梁双柱墩的影响较小,其受力和变形图介于单柱墩和刚性系梁双柱墩之间,且更偏向于单柱墩,因此柔性系梁双柱墩也可以采用集中塑性铰方法计算。
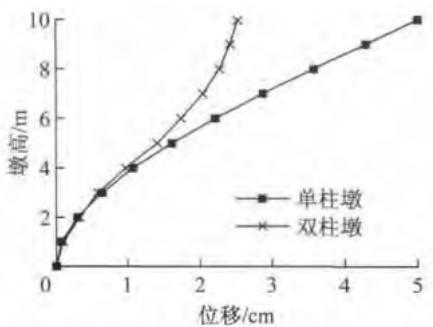
a 屈服位移
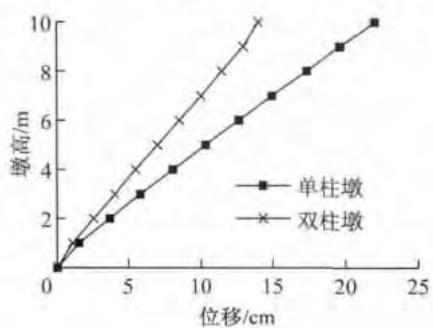
b 塑性位移
图 4 控制阶段位移分布图
Fig. 4 Displacement distribution of critical stages
3 双柱墩弹塑性位移能力简化方法
通过对双柱墩动轴力和塑性铰机制的影响分析,并与单柱墩进行比较,发现双柱墩的弹塑性位移能力可在单柱墩的基础之上进行推导。本节从墩顶屈服位移和墩顶塑性位移两方面来分析双柱墩弹塑性位移能力简化计算方法。
3.1 双柱墩墩顶屈服位移简化公式
单柱墩墩顶屈服位移计算公式可根据屈服状态时沿墩底到墩顶的曲率积分求解,具体计算公式如下:
式中: \Delta_{\mathrm{y}}^{\mathrm{s}} 表示屈服墩顶位移, M_{\mathrm{y}} 表示屈服墩底弯矩, EI_{\mathrm{eff}} 表示屈服等效刚度, \phi_{\mathrm{y}} 表示屈服曲率, L 为单柱墩墩高。
当系梁刚度为无穷大时,墩顶和墩底屈服弯矩大小相等,忽略动轴力的影响,刚性系梁双柱墩墩顶屈服位移计算公式为
式中: \Delta_{\mathrm{y}}^{\mathrm{u}} 表示刚性系梁双柱墩屈服时墩顶位移; M_{\mathrm{y}}^{\mathrm{u}} 和 M_{\mathrm{y}}^{\mathrm{d}} 分别为墩顶和墩底屈服弯矩,两者大小相同且与 M_{\mathrm{y}} 一致。由上可知,刚性系梁双柱墩墩顶屈服位移是单柱墩墩顶屈服位移的一半,与图 4 中结果一致。当系梁为柔性时,墩柱仅在墩底产生塑性铰,墩顶的弯矩很小,完全可以不用考虑动轴力的影响,直接沿墩底到反弯点距离对屈服状态时曲率进行线性积分,即可得到柔性系梁双柱墩墩顶屈服位移。
3.2 双柱墩墩顶塑性位移计算公式
根据图 4 中单柱墩和刚性系梁双柱墩的塑性位移分布可知:双柱墩亦可以像单柱墩一样采用集中塑性铰计算墩顶塑性位移,即结构进入塑性以后,结构的变形相当于绕等效塑性较长度内一点的转动。因此,选择合理的等效塑性较长度是准确预测墩顶塑性位移能力的关键。
近二十年来,许多学者提出过等效塑性较长度经验计算公式。 Mortezaei 等14总结了前人通过不同试验方法和考虑不同因素所提出的 14 个等效塑性较长度计算公式。但是目前被 Caltrans 和 AASHTO 抗震设计标准以及大多数学者所接受的是 Priestley 等12提出的等效塑性较长度经验计算公式,如下式所示:
式中: l_{\mathrm{p}} 为等效塑性铰长度, H 为塑性铰截面到反弯点的距离, f_{\mathrm{y}} 为纵向钢筋抗拉强度标准值, d_{s} 为纵向钢筋直径。我国现行抗震规范也采用这一公式,同时与墩柱截面宽度的 2/3 比较,取最小值。
塑性转角计算公式为
式中: \theta_{\mathrm{u}} 为塑性转角; \phi_{\mathrm{u}}, \phi_{\mathrm{y}} 分别表示截面极限破坏状态曲率和等效屈服曲率; K 为延性安全系数。国外抗震规范中没有明确对塑性转角进行一定的折减,而我国规范根据我国规则桥梁适用范围,对塑性转角采用延性安全系数 2 来进行折减。本文计算塑性转角时,也考虑 K = 2 时的延性安全系数折减。
根据集中塑性铰模型,得出最后的双柱墩墩顶塑性位移能力为
即墩顶的塑性位移是绕墩底等效塑性较长度中点的转动。
最后得出双柱墩墩顶位移能力为
这样,就可以基于截面层次对关键截面(墩底)进行曲率分析,得到关键截面的屈服曲率和破坏曲率,然后就可以避开繁琐的 Pushover 分析方法,从而对双柱墩的弹塑性位移能力进行简化计算。
4 简化计算方法的误差分析
影响等效塑性较长度的因素很多,如轴压比、塑性铰区域内的剪应力、纵向钢筋和横向钢筋的力学性质、混凝土的标准强度、塑性铰区域内的配筋率等。其中,轴压比和墩柱的长细比是影响等效塑性铰长度的关键因素。因此,基于这两个参数来讨论双柱墩弹塑性位移能力简化计算方法的适用性。桥梁抗震规范中对规则桥梁定义为轴压比小于 30\% ,长细比在 2.5 \sim 10.0 之间,因此本文分别取轴压比 5\% , 10\% , 20\% , 30\% 及长细比 2.5, 5.0, 7.5, 10.0 讨论简化计算公式的适用性。
4.1 屈服位移和塑性位移的数值计算和简化计算对比
双柱墩在 Pushover 单调递推过程中,一个墩柱承受动轴拉力,另一个墩柱承受动轴压力。在 30\% 轴压比范围内,双柱墩的屈服是受关键截面最外侧受拉钢筋屈服拉应变控制的,即受动轴拉力墩控制屈服;双柱墩的破坏是受关键截面核心混凝土边缘极限压应变控制的,即受动轴压力墩控制破坏。表 1 中列出对刚性系梁双柱墩运用 Pushover 分析方法得出的控制墩柱的屈服位移和塑性位移的数值解和运用简化计算公式得出的相应值的对比。
由表 1 对屈服位移进行分析可知:利用简化公式得出的墩顶屈服位移值比运用 Pushover 分析方法得出的屈服位移值略大,其原因为双柱墩中由于动轴力的影响,截面屈服曲率会小于不考虑动轴力时的屈服曲率,但总体来说在轴压比小于 30\% 时具有很好的精度。采用基于性能抗震设计的结构要求具有很好的延性,结构进入屈服之后、破坏之前会有足够的延性安全度,因此可以采用该简化计算公式计算双柱墩墩顶屈服位移。
由表 1 对塑性位移进行分析可知:随着轴压比的增大,塑性位移都将减小;对于长细比较小时,如长细比为 2.5 时,随着轴压比的增加,简化计算塑性位移值与 Pushover 分析塑性位移值的误差越来越大,这时得到的墩顶塑性位移偏于不安全;随着长细比的增大,简化计算塑性位移值逐渐小于 Pushover 分析塑性位移值,并随着轴压比的减小,简化计算方法比 Pushover 分析方法更安全。
4.2 破坏位移的数值计算和简化计算对比
对结构采用基于性能抗震设计方法时,需对结构进行位移验算,确定结构在规定地震概率水准作用下不发生倒塌,使结构在地震作用下的墩顶需求位移在破坏位移之内,即位移需求能力比要小于 1。表 2 列出刚性系梁双柱墩和与双柱墩相同构造的单柱墩通过运用 Pushover 分析方法得出的破坏位移数值解和运用简化计算公式得出相应值的对比。
表 1 屈服位移和塑性位移对比表
Tab. 1 Comparison of yield displacement and plastic displacement
| 轴压比/% | 长细比 | 屈服位移数值解/m | 屈服位移简化公式计算值/m | 误差/% | 塑性位移数值解/m | 塑性位移简化公式计算值/m | 误差/% |
|---|---|---|---|---|---|---|---|
| 5 | 2.5 | 0.005 0 | 0.005 3 | 6.00 | 0.028 8 | 0.035 8 | 24.31 |
| 5.0 | 0.020 3 | 0.021 0 | 3.45 | 0.108 5 | 0.104 7 | -3.50 | |
| 7.5 | 0.046 3 | 0.047 3 | 2.16 | 0.242 9 | 0.206 3 | -15.07 | |
| 10.0 | 0.082 5 | 0.084 1 | 1.94 | 0.427 2 | 0.340 5 | -20.29 | |
| 10 | 2.5 | 0.005 6 | 0.005 8 | 3.57 | 0.021 3 | 0.026 9 | 26.29 |
| 5.0 | 0.021 3 | 0.023 1 | 8.45 | 0.086 3 | 0.087 7 | 1.62 | |
| 7.5 | 0.048 8 | 0.051 9 | 6.35 | 0.181 5 | 0.155 0 | -14.60 | |
| 10.0 | 0.087 5 | 0.092 3 | 5.49 | 0.318 3 | 0.255 9 | -19.60 | |
| 20 | 2.5 | 0.005 9 | 0.006 7 | 13.56 | 0.011 7 | 0.017 0 | 45.30 |
| 5.0 | 0.023 8 | 0.027 0 | 13.45 | 0.046 3 | 0.049 8 | 7.56 | |
| 7.5 | 0.053 8 | 0.060 6 | 12.64 | 0.097 4 | 0.098 0 | 0.62 | |
| 10.0 | 0.096 3 | 0.107 8 | 11.94 | 0.170 4 | 0.161 8 | -5.05 | |
| 30 | 2.5 | 0.006 4 | 0.008 1 | 26.56 | 0.007 6 | 0.011 9 | 56.58 |
| 5.0 | 0.025 9 | 0.032 5 | 25.48 | 0.030 0 | 0.034 9 | 16.33 | |
| 7.5 | 0.058 8 | 0.073 1 | 24.32 | 0.066 3 | 0.068 7 | 3.62 | |
| 10.0 | 0.103 8 | 0.130 0 | 25.24 | 0.112 4 | 0.113 5 | 0.98 |
注:误差 = (简化公式计算值一数值解值)/ 数值解值。负值为偏于安全。
表 2 破坏位移对比表
Tab. 2 Comparison of collapse displacement
| 轴压比/% | 长细比 | 双柱墩破坏位 移数值解/m | 双柱墩破坏位移简 化公式计算值/m | 误差/% | 单柱墩破坏位 移数值解/m | 单柱墩破坏位移简 化公式计算值/m | 误差/% |
|---|---|---|---|---|---|---|---|
| 5 | 2.5 | 0.0338 | 0.0410 | 21.30 | 0.0620 | 0.0550 | 12.72 |
| 5.0 | 0.1288 | 0.1257 | -2.41 | 0.2070 | 0.2175 | -4.83 | |
| 7.5 | 0.2891 | 0.2536 | -12.28 | 0.4338 | 0.4875 | -11.02 | |
| 10.0 | 0.5097 | 0.4246 | -16.70 | 0.7446 | 0.8713 | -14.54 | |
| 10 | 2.5 | 0.0269 | 0.0326 | 21.19 | 0.0502 | 0.0444 | 13.17 |
| 5.0 | 0.1075 | 0.1108 | 3.07 | 0.1706 | 0.1756 | -2.85 | |
| 7.5 | 0.2302 | 0.2069 | -10.12 | 0.3587 | 0.3931 | -8.75 | |
| 10.0 | 0.4058 | 0.3482 | -14.19 | 0.6156 | 0.6969 | -11.66 | |
| 20 | 2.5 | 0.0177 | 0.0237 | 33.90 | 0.0379 | 0.0325 | 16.75 |
| 5.0 | 0.0700 | 0.0767 | 9.57 | 0.1338 | 0.1294 | 3.41 | |
| 7.5 | 0.1511 | 0.1587 | 5.03 | 0.2863 | 0.2894 | -1.05 | |
| 10.0 | 0.2667 | 0.2696 | 1.09 | 0.4953 | 0.5113 | -3.13 | |
| 30 | 2.5 | 0.0140 | 0.0200 | 42.86 | 0.0334 | 0.0248 | 34.90 |
| 5.0 | 0.0559 | 0.0674 | 20.57 | 0.1205 | 0.0984 | 22.42 | |
| 7.5 | 0.1250 | 0.1419 | 13.52 | 0.2615 | 0.2204 | 18.66 | |
| 10.0 | 0.2162 | 0.2435 | 12.63 | 0.4559 | 0.3897 | 16.98 |
注:误差 = (简化公式计算值一数值解值)/ 数值解值。负值为偏于安全。
由表 2 双柱墩破坏位移能力误差分析可知:对于低长细比高轴压比时,运用简化计算公式计算误差较大且偏于不安全。当轴压比在 5\% \sim 20\% 时、长细比在 5.0 \sim 10.0 之间时,在工程运用范围内该简化计算公式的误差是可以接受的。该误差分析可以从以下两方面来解释:①首先目前规范中计算单柱墩位移能力都是基于等效塑性较长度的经验公式,从表 2 中可以看出运用该公式计算单柱墩位移能力本身就存在一定误差,而本文推导出的双柱墩经验公式产生的误差与单柱墩产生的误差相差不大,特别是在高轴压比时运用该简化公式计算得出的双柱墩位移能力的误差比单柱墩更小。②在桥梁抗震设计中,基础的抗震设计起主要控制作用。在地震作用下桥墩的弹塑性位移能力相对于地震需求而言,其富裕度较大。因此对于桥墩在地震作用下的弹塑性位移能力验算精度的要求也不高,本文在限定轴压比为 5\% \sim 20\% 、长细比为 5.0 \sim 10.0 时运用双柱墩位移能力简化计算公式产生的最大误差为 20\% (偏于不安全) 是完全可以接受的。另随着长细比的增加和轴压比的减小,简化计算的墩顶破坏位移小于 Pushover 分析得出的墩顶破坏位移,得出的结果是偏于安全的。根据表中数据变化趋势可推测出当轴压比较高时,如大于 30\% 时,该简化计算公式可偏安全地适用于长细比大于 10\% 的双柱墩墩柱。
5 结论
(1)双柱墩从开始受力经历屈服到破坏过程中,动轴力在墩柱截面内产生的正应力相对于弯矩在墩柱截面内产生的正应力更小,同时双柱墩墩柱与单柱墩等效刚度相差不大,因此可以不考虑动轴力对双柱墩弹塑性位移能力的影响。
(2)双柱墩墩顶塑性位移亦可看成绕墩底等效塑性较长度内一点的转动,柔性系梁双柱墩墩顶塑性位移介于刚性系梁双柱墩与单柱墩墩顶塑性位移之间。
(3)运用墩顶屈服位移简化公式得出的双柱墩墩顶屈服位移比实际墩顶屈服位移略大,对于规则桥梁而言,其精度在工程可接受范围之内。运用墩顶塑性位移简化公式得出的双柱墩墩顶塑性位移在低轴压比高长细比时误差较小,且是偏于安全的。
(4)运用双柱墩弹塑性位移能力简化计算方法计算出的破坏位移在轴压比为 5\% \sim 20\% 、长细比为 5.0 \sim 10.0 时,在地震工程运用范围内,具有很好的适用性,并随着长细比的增加和轴压比的减小,简化计算的墩顶破坏位移小于 Pushover 分析得出的墩顶破坏位移,得出的结果是偏于安全的。
Priestley M J N. Performance-based seismic design [J]. Engineering Structures, 2000, 25(14):1803. ↩ ↩ ↩
Park R, Ruitong D. Ductility of doubly reinforced concrete beam sections[J]. ACI Structural Journal, 1988, 85(2): 217. ↩
Bayrak O, Sheikh S A. Plastic hinge analysis [J]. ACI Structural Journal, 2001, 127(9): 1092. ↩
Bae S, Mieses A M, Bayrak O. Inelastic buckling of reinforcing bars[J]. Journal of Structural Engineering, ASCE, 2005,131(2):314. ↩
Dhakal R P, Fenwick R C. Detailing of plastic hinges in seismic design of concrete structures[J]. ACI Structural Journal, 2008, 105(6):740. ↩
Dowell R K, Hines E M. Plastic hinge length of reinforced concrete bridge columns[J]. ACI Structural Journal, 2008, 105 (3): 290. ↩
Hines E M, Dazio A, Seible F. Cyclic tests of structural walls with highly-confined boundary elements [R]. San Diego: University of California, 2002. ↩
Bae S, Bayrak O. Seismic performance of full-scale reinforced concrete columns[J]. ACI Structural Journal, 2008, 105(2): 123. ↩
Berry M P, Lehman D E, Lowes L N. Lumped-plasticity models for performance simulation of bridge columns[J]. ACI Structural Journal, 2008, 105(3): 270. ↩
沈星,叶爱君,王晓伟. 柔性横系梁双柱墩的抗震行为分析 [J]. 同济大学学报:自然科学版,2013,41(3):342.
SHEN Xing, YE Aijun, WANG Xiaowei. Seismic behavior analysis for link beam of double-column bent[J]. Journal of Tongji University: Natural Science, 2013,41(3):342. ↩ ↩韦晓,范立础,王君杰. 考虑桩 - 土 - 桥梁结构相互作用振动台试验研究 [J]. 土木工程学报,2002,35(4):91.
WEI Xiao, FAN Lichu, WANG Junjie. Shake table test on soil-pile-structure interaction [J]. China Civil Engineering Journal, 2002, 35(4):91. ↩Priestley M J N, Seible F, Calvi C M. Seismic design and retrofit of bridge[M]. New York: Wiley & Sons, 1996. ↩ ↩ ↩ ↩
Chang G A, Mander J B. Seismic energy based fatigue damage analysis of bridge columns: part I—evaluation of seismic capacity[R]. New York: NCEER, 1994. ↩
Mortezaei A, Ronagh H R. Plastic hinge length of reinforced concrete columns subjected to both far-fault and near-fault ground motions having forward directivity[J]. The Structural Design of Tall and Special Buildings, 2013, 22(12):903. ↩