王晓伟, 叶爱君
(同济大学土木工程防灾国家重点实验室, 上海 200092)
摘要: 该文比较了中国和日本两国桥梁抗震设计规范中群桩基础的抗震设计方法, 并结合一座连续梁桥分别采用中日规范进行抗震分析与比较。“中国规范”要求桩基在地震中保持弹性工作状态, 而“日本规范”允许桩基在特殊情况下塑性屈服;“中国规范”对群桩基础仅进行强度指标验算, 而“日本规范”对强度、位移或转角进行验算;中日规范的群桩基础抗震计算方法基本相同。实例计算表明: 对于桥墩的地震需求,“日本规范”明显比“中国规范”大;但对于群桩基础的地震需求, 当桥墩屈服后, 基本一致;基础的转角不控制设计。
关键词:桥梁抗震;规范比较;群桩基础;延性设计
中图分类号:U442.5’5 文献标识码:A 文章编号:1009-7716(2012)11-0125-05
Comparison and Study of Group Pile Foundation Design in China - Japan Bridge Seismic Design Code
Wang Xiaowei, Ye Aijun(125)
Abstract: The article compares the seismic design methods of group pile foundation in the bridge seismic design code of China and Japan, and carries out the seismic analysis and comparison of a regulated continuous beam bridge separately according to the standards of China and Japan. The pile foundation is required to keep in the elastic working state during an earthquake according to the Chinese Code, but the Japanese Code allows the pipe foundation is in plastic yielding state under the special condition. The Chinese Code only checks and calculates the intensity index for the group pile foundation, but the Japanese Code checks and calculates the intensity, displacement or corner. The seismic calculation methods of group pile foundation in the Chinese and Japanese codes are basically same. The practical calculation shows that the "Japanese Code" is obviously higher than the "Chinese Code" for the earthquake demands of bridge pier, but these codes are basically identical for the earthquake demands of group pile foundations after the yielding of bridge pier. The corner of foundation does not control the design.
Keywords: seismic design of bridge, comparison of standards, group pile foundation, ductility design
0 引言
近些年来, 世界各地地震频发, 其中影响较大的是 2008 年的中国汶川地震和 2011 年的日本东北地方太平洋近海地震。桥梁在地震中的安全对于震后救灾意义重大, 而先进、可靠的抗震设计规范是保障桥梁抗震性能的基础。中日两国在总结震害经验的基础上, 结合本国国情, 于 2011 年分别颁布或修订了最新的桥梁抗震设计规范, 即《城市桥梁抗震设计规范》(以下简称“中国规范”)1和《道路桥示方书(IV 耐震设计篇)・同解说》(以下简称“日本规范”)2。
“中国规范”和“日本规范”均采用两阶段抗震设计, E1 地震(“日本规范”中称为 L1 地震)为发生概率较大的小、中地震, E2 地震(“日本规范”中称为 L2 地震)为发生概率较小的大地震, 其中日本规范中的 L2 地震根据地震成因又分为 I 型(板块碰撞型)和Ⅱ型(大陆直下型);“中国规范”规定桥梁类型分为甲、乙、丙、丁四类, 而“日本规范”仅分为 A、B 两类, 其中 B 类桥梁为抗震性能要求较高的国道、城市高速道路或地震多发地区等处的桥梁。“中国规范”对于桥梁的分类更为细化。
桥梁抗震设计的基本思想和设计准则是制定规范的最重要之处, 它决定了抗震设计要达到的目标、采用的设计地震动水平和地震反应的计算方法等。抗震性能要求方面, 两规范总体上较为相似,“中国规范”规定在 E1 地震下, 各类桥梁的所有部件均保持在弹性范围内并且震后立即使用, 在 E2 地震下, 从甲类桥梁的允许产生轻微损伤到丁类桥梁的不致倒塌, 呈现由高到低的性能等级要求;而“日本规范”分为三级抗震性能要求, 即在 L1 地震下, A、B 类桥梁均保持原有功能, 各部件在弹性范围内工作(性能等级 1), L2 地震下, B 类桥梁允许产生一定的损伤, 但能够经快速修复恢复原有功能(性能等级 2), A 类桥梁不产生致命性的结构损伤(性能等级 3)。
在历次地震震害中, 群桩基础的震害较为常见, 大量的桥梁抗震设计实践也表明, 群桩基础往往是抗震薄弱部位, 由地震控制设计, 是整座桥梁抗震设计的关键。而对于群桩基础的抗震设计, 由于目前的研究还不够成熟, 各国规范往往根据震害资料做一些规定, 其中日本规范相对较为细致。
本文首先比较了中日规范的群桩基础抗震设计方法, 具体从性能要求、验算指标、需求和能力值的计算四方面进行比较, 结合一座连续梁桥的实例, 进行中日规范中关于群桩基础抗震设计的比较研究, 并得出相关结论。
1 群桩基础抗震设计方法比较
1.1 群桩基础抗震性能要求
表 1 从总体上对中日规范中群桩基础的抗震性能要求进行了比较。
表 1 中日规范群桩基础抗震性能要求比较表
| 规范 | \multicolumn{2}{c | }{中国规范} | \multicolumn{2}{c | }{日本规范} |
|---|---|---|---|---|
| 震别 | E1 | E2 | L1 | L2 |
| 性能要求 | 力学性能保持弹性,不屈服 | 力学性能保持弹性,不屈服 | 力学性能保持弹性,不屈服 | 尽量保持弹性,特殊情况允许屈服 |
“中国规范”规定, 在 E1 和 E2 地震下桩基均保持在弹性范围内工作, 不允许桩身屈服;在桥梁采用延性设计的情况下, E2 地震下依靠墩柱端部形成塑性铰以耗散地震能量。
“日本规范”规定, 在 L1 地震下桩身亦不允许屈服, 力学性能保持弹性状态, 而在 L2 地震下, 首先应尽可能使塑性铰出现在墩柱端部。但在某些特殊情况下, 比如:(1)桥墩在某水平方向有足够的屈服强度(如墙式墩), 在地震中难以形成塑性铰;(2)桩基处在土质液化较为严重的区域这两种情况, 允许桩顶产生有限的塑性变形, 以消耗地震能量, 减轻地震对整体结构的损伤。值得注意的是, 这两种特殊情况下要求墩身和上部结构均保持弹性工作状态。与“中国规范”相比,“日本规范”更为灵活。
1.2 抗震验算指标
验算指标是群桩基础达到抗震性能要求的依据, 合理的抗震验算指标对于群桩基础的抗震设计至关重要。
“中国规范”规定桩基在地震下力学性能保持在弹性范围内, 验算强度指标, 即单桩的轴向抗压、抗拉承载力和抗弯承载力, 并且仅对 E2 地震进行验算。
“日本规范”规定在 L1 地震下, 采用容许应力法验算群桩基础的承载力, 即验算最不利截面的轴向应力和剪切应力, 以及群桩基础的水平位移。在 L2 地震下, 当要求群桩基础保持弹性时, 验算桩身的抗弯能力、抗剪能力, 以及基础的转角。验算转角基础水平位移的目的是确保桥墩在塑性变形引起残余位移的情况下, 群桩基础仍有足够的变形能力;当群桩基础作为主要耗能部件, 即在特殊情况下允许塑性化的情况下, 验算桩基的反应塑性率, 以及基础的转角, 目的在于将群桩基础产生的损伤限定在可修补的范围内, 并且避免因桩基的转角过大导致上部结构的残留位移过大的问题。
由此可见, 两种规范关于抗震验算指标的规定, 主要区别是“日本规范”需验算群桩基础的水平位移、转角。
1.3 地震需求计算方法
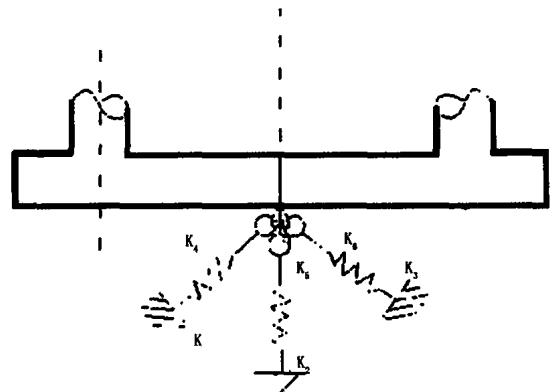
对于群桩基础的地震需求计算方法, 中日两国规范的相关规定基本相同。两种规范首先将群桩基础简化进行承台底内力的计算, 如图 1 所示, 区别在于,“中国规范”的桩基础刚度矩阵仅考虑六个对角元项(“六弹簧”模型), 而“日本规范”还额外考虑了平动、转动耦合刚度的非对角元项。此外, 当桥墩在地震中保持弹性状态的情况下, 直接根据桥墩的地震反应值计算承台底的地震需求;但当桥墩在地震中塑性屈服后, 中日规范均采用能力保护方法计算承台底的地震需求。
得到承台底内力后, 中日规范都按静力方法反算桩身内力, 区别在于土层的水平抗力系数的计算方法略有不同。需要说明的是,“日本规范”中群桩基础的水平位移、转角值亦采用静力方法进行。
1.4 抗震能力计算方法
抗震能力值表征了部件抵抗地震作用的能力, 与土体的力学特性、桩基构件的截面特征及其弹塑性发展历程有关。
“中国规范”规定, 群桩基础的单桩轴向抗压承载能力在静力规范值的基础上考虑 1.2 的地震提高系数;抗拉承载力考虑 1.5 的地震提高系数;抗弯承载力通过弯矩 - 曲率分析得到, 构件的弹塑性发展历程如图 2 所示5。 “日本规范”规定, L1 地震下, 采用容许应力法进行群桩基础抗震能力验算, 单桩的容许应力值以及群桩基础的水平位移能力值根据《道路标示方书(下部构造篇)・同解说》3相关规定得到, 桩径 1.5\mathrm{m} 以内时, 水平位移容许值为 15\mathrm{~mm}。L2 地震下, 桩基的抗弯能力值采用三线性的弯矩 - 曲率分析得到, 弹塑性发展历程如图 3 所示。桩基的转角能力值为 0.025\mathrm{~rad}, 该值的设定基于对以往震害的调查。需要说明的是, 2002 年版的“日本规范”需验算水平位移和转角, 分别为 400\mathrm{~mm} 和 0.025\mathrm{~rad}, 但条文说明中指出, 实际经验表明水平位移一般很小, 不控制设计, 所以 2002 年以后的规范里只提出了转角值。
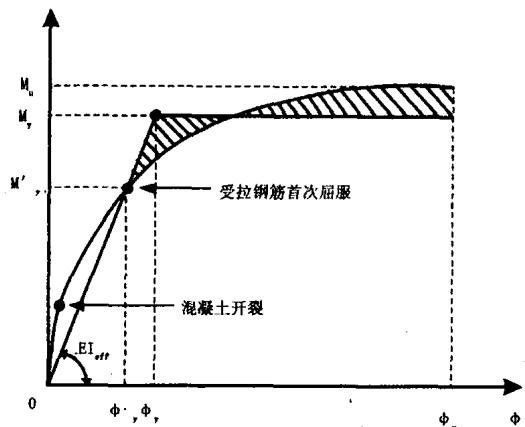
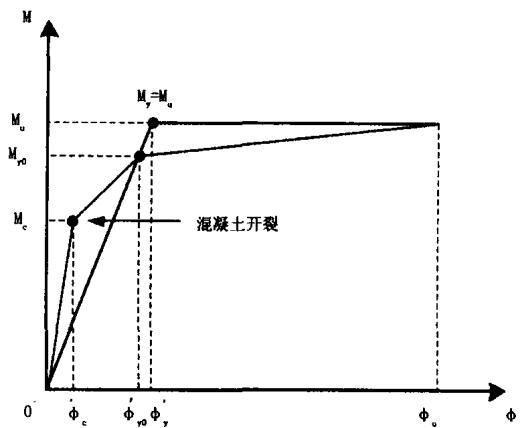
图 3“日本规范”规定的曲线图
2算例
2.1结构概况
选取某城市高架桥的一联连续梁桥 (3\times 22\mathrm{~m}) 为工程实例, 分别根据中日规范进行群桩基础的抗震分析。桥梁横断面及基础布置如图 4、图 5 所示。
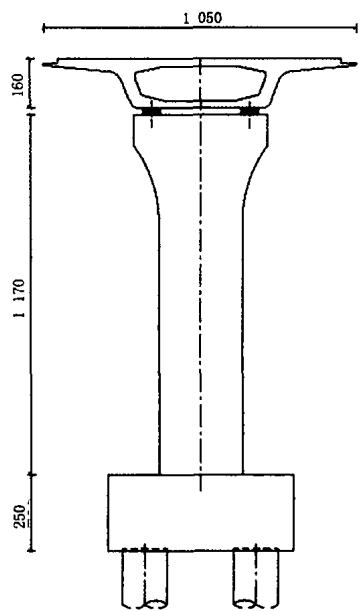
图 4 桥梁横断面图(单位:cm)
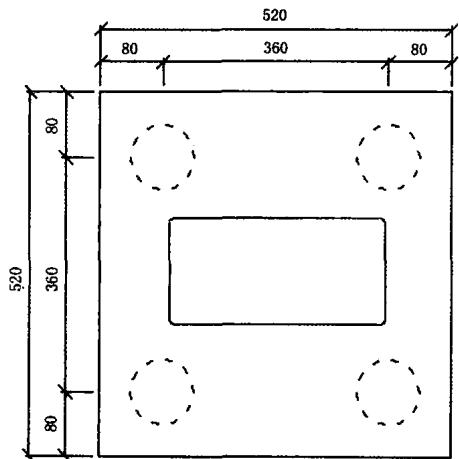
图 5 基础布置图(单位:cm)
桥墩为实心矩形墩, 墩高 11.7\mathrm{~m}, 墩底顺桥向宽 1.3\mathrm{~m}, 横桥向宽 2.8\mathrm{~m}。群桩基础采用 4 根直径 1\mathrm{~m}, 长 43.5\mathrm{~m} 的摩擦桩, 支座与垫石总高度为 0.3\mathrm{~m}, 支座布置方式为顺桥向中间设一个固定墩, 其余各支座滑动, 横桥向各支座均固定。墩柱和桩基的配筋方案如图 6 所示。
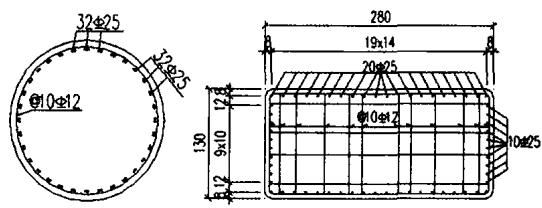
图 6 桩基与墩柱配筋图(单位:cm)
上部结构、立柱、基础分别采用 C50、C40、C30 混凝土。一联三跨的主梁总重(包括二期恒载)为 10350\mathrm{~kN}。全部恒载作用下, 中墩支座反力为 3795\mathrm{~kN}, 边墩支座反力为 1380\mathrm{~kN}。桥墩质量为 112.9\mathrm{~t}, 盖梁质量为 15.1\mathrm{~t}, 承台质量 101.6\mathrm{~t}。
2.2设计地震参数及分析方法
为保证两种规范在相同的地质条件下进行抗震分析比较, 对该工程所处位置的相关地震参数的规定如下。“中国规范”中, 该工程所在场地土的 m 系数为 15000\mathrm{~kN / m^4}, 单桩抗压承载力为 6500\mathrm{~kN}, 抗拉承载力为 2850\mathrm{~kN}, 无液化土层。根据现行《中国地震动参数区划图》查得该地区设计基本地震加速度值为 0.15\mathrm{~g}, 特征周期为 0.45\mathrm{~s}, 对应设计地震分区为第三区, 局部场地类别为Ⅱ类, 取特征周期为 0.45\mathrm{~s}。该桥是交通枢纽位置上的桥梁, 为乙类, 结合设防烈度, 选用 A 类抗震设计方法。地震调整系数, E1 地震作用为 0.61, E2 地震作用为 2.2。E1 和 E2 地震作用水平设计反应谱为:
其中, S = 2.25A, A 为地震加速度峰值。
“日本规范”中, 该工程为 B 类桥梁, Ⅲ类地基, 地域类别为 C 类(修正系数 C_{z} = 0.7), 无液化土层;值得注意的一点, 由于中国和日本的混凝土规范中的强度试验方法有所差别, 中国混凝土规范规定混凝土轴心抗压强度试验采用 150\mathrm{~mm}\times 150\mathrm{~mm}\times 300\mathrm{~mm} 的长方体试件, 而日本规范确定混凝土强度的试验所采用的试件尺寸为 150\mathrm{~mm}\times 300\mathrm{~mm} 和 150\mathrm{~mm}\times 200\mathrm{~mm} 的圆柱体, 根据构件强度与尺寸的转换关系, 该桥下部墩柱所采用的中国 C40 混凝土相当于日本相关规范中强度等级为 30\mathrm{~MPa} 的混凝土, 桩基所采用的中国 C30 混凝土相当于日本相关规范中等级强度为 24\mathrm{~MPa} 的混凝土。
该桥结构形式简单, 属于规则桥梁, 故“中国规范”在 E1、E2 地震下均采用规则桥梁的单振型反应谱法, 而“日本规范”在 L1 地震下采用震度法, L2 地震下采用地震时采用保有耐力法。
根据以上基本地震参数的规定, 分别基于“中日规范”对该桥下部结构, 特别是群桩基础, 进行抗震分析, 限于篇幅, 论文仅针对该桥梁的纵桥向设置固定支座的中墩的横桥方向进行大地震下(“中国规范”的 E2 地震,“日本规范”的 L2 地震)的抗震性能分析比较。
2.3计算模型
2.3.1“中国规范”
从该桥的结构特点可知, 横桥向每个桥墩均为固定墩, 各墩等高, 主梁横向刚度较大, 并结合规范相关规定, 简化为单跨桥梁, 建立单自由度计算模型, 质量中心位于主梁横断面质心处, 计算中取主梁质心距支座顶部的距离为 0.8\mathrm{m}。群桩基础采用“六弹簧”模型模拟, 基础刚度参数见表 2 所列。
表 2“中国规范”基础刚度参数表
| 刚度类型 | 方向 | 刚度 |
|---|---|---|
| 平动刚度/kN·m^{-1} | 横向 | 3.49E+05 |
| 纵向 | 3.49E+05 | |
| 竖向 | 2.44E+06 | |
| 转动刚度/(kN·m/Rad) | 绕纵向 | 8.96E+07 |
| 绕横向 | 8.96E+06 | |
| 绕竖向 | 2.73E+06 |
在横桥向对质量中心施加单位力, 可得质量中心横向位移及公式 (2) 中相关参数, 既得单自由度模型的换算质量为 396(\mathrm{t}), 等效刚度为 21900(\mathrm{kN} / \mathrm{m}), 故 E1 地震下的自振周期为 0.85(\mathrm{s})。
2.3.2“日本规范”
根据“日本规范”的规定可知, 该桥在横桥向由一座以上的下部结构所构成, 需建立全桥的集中质量模型, 模型的地基等效弹簧刚度可根据场地土条件及群桩基础的布置形式求得, 如表 3 所列。可见根据两规范得到的地基弹簧系数略有差异, 这主要是由于基于两规范的计算方法的不同所致, 其中“日本规范”还考虑了弹簧的平动与转动的耦合刚度, 比“六弹簧”模型更精确。
在主梁、桥墩(包括盖梁)、承台的各质点处施加横桥向的相当于该质点重量 W_i 的水平力 W_i, 求得该工况下各质点的横桥向水平位移 U_i, 其中上部结构横桥向的惯性力作用位置为主梁的质心处, 再根据公式(2)和(3)计算震度法下的该桥的
表 3“日本规范”基础的地基弹簧系数表
| 方向 | 刚度 |
|---|---|
| 竖向平动刚度Kv/kN·m^{-1} | 2.38E+06 |
| 水平向平动刚度A/kN·m^{-1} | 3.84E+05 |
| 平动、转动A/kN·rad^{-1} | 7.58E+05 |
| 耦合刚度A/(kN·m)·m^{-1} | 7.58E+05 |
| 转动刚度A/(kN·m)·rad^{-1} | 8.34E+06 |
横桥向固有周期。
2.4计算结果
2.4.1桥墩屈服状态的判别与比较
“中国规范”中 E2 地震横桥向设计时, 先假定桥墩处于弹性状态, 不进行刚度折减, 横向自振周期仍为 0.85(\mathrm{~s}), 则可得墩底组合弯矩为 20800(\mathrm{kN}\cdot \mathrm{m}), 此时采用材料的标准值求得墩底截面的横向等效屈服弯矩为 21700(\mathrm{kN}\cdot \mathrm{m}), 故墩底截面保持弹性状态, 不必进行位移能力验算。在此基础上, 对群桩基础的抗震性能进行分析。
“日本规范”中 L2 地震分为 I 型和Ⅱ型地震两类, 采用地震时保有水平耐力法, 设计水平地震烈度 K_{hc} 分别为 0.40、0.39, 得到桥墩的反应塑性率 \mu_R 分别为 1.82、1.80, 可知桥墩进入屈服状态 (\mu_R > 1), 但未超过容许的反应塑性率(I、Ⅱ型地震分别为 2.03、4.15), 且保有水平耐力 P_u < 1.5 K_{hc} \cdot W, 即桥墩在水平向不具有足够的屈服水平耐力, 这种情况下以桥墩作为地震中的主要耗能部件, 桩基不允许屈服。
在大地震下,“中国规范”计算得桥墩保持弹性工作状态, 而根据“日本规范”, 桥墩已经进入塑性状态。比较可知,“日本规范”的设计地震力更大。
2.4.2群桩基础的抗震验算与比较
“中国规范”计算得桥墩保持弹性, 直接求得承台底内力后进行群桩基础的抗震验算;而根据“日本规范”, 群桩基础的抗震性能验算应采用考虑了桥墩塑性反应的设计水平烈度, I 、Ⅱ型地震用于验算群桩基础的设计水平烈度分别为 0.47、0.48。中日规范的验算结果比较见表 4 所列。
在大地震下, 按“中国规范”设计, 群桩基础通过验算, 其中抗压承载力能力值较大, 这与考虑了 2.0 的地震提高系数有关。而依据“日本规范”, 该桩基抗弯承载力不足, 未通过验算, 值得注意的是, 在该算例中, 基础转角并未对抗震设计起控制作用。
此外, 虽然“中国规范”中桥墩未进入屈服状态, 但需求与能力值较为接近, 故假设桥墩塑性屈服, 采用能力保护方法进行群桩基础的抗震计算, 由表 4 结果可知, 这种情况下中日规范的群桩基础的地震需求基本相同。
表 4 大地震下中日规范群桩基础抗震验算结果比较一览表
| 规范 | 验算指标 | 需求值 | 能力值 | 能力/需求 |
|---|---|---|---|---|
| 中国规范 | 抗压承载力/kN | 5 294 | 13 000 | 2.46 |
| 抗拉承载力/kN | 2 273 | 3 562 | 1.57 | |
| 抗弯承载力/kN·m | 513(736)* | 1 229(751)* | 2.40(1.02)* | |
| 日本规范 | 抗弯承载力/kN·m# | 770(788)* | 764(722)* | 0.99(0.92)* |
| 抗剪承载力/kN | 710(726)* | 1 335(1590)* | 1.88(2.19)* | |
| 基础转角/nd | 0.003 | 0.02 | 6.67 |
注:x 假设桥墩屈服, 按能力保护方法计算所得的结果;
※括号内数值为 L2 地震下Ⅱ型地震对应的结果;
#两排桩基均屈服, 此处仅列出最不利单桩的情况。
3结论
本文首先从总体上比较中日桥梁抗震设计规范, 然后从抗震性能要求、验算指标、地震反应值(需求值)、能力值计算方法这四方面对两规范中的群桩基础抗震设计方法进行比较, 最后结合计算实例, 得到以下结论:
(1)“中国规范”要求群桩基础在地震中保持弹性工作状态, 而“日本规范”则允许桩基在特殊情况下屈服, 利用桩基的延性抗震。
(2)“中国规范”仅对群桩基础进行强度指标验算, 而“日本规范”进行强度、位移或转角验算。
(3)中日规范的群桩基础抗震计算方法基本相同, 都是首先计算承台底的地震内力需求, 然后采用静力方法反算桩基内力与位移、转角。桥墩屈服后, 中日规范均采用能力保护方法计算基础的抗震需求。
(4)实例计算表明: 对于桥墩的地震需求,“日本规范”明显比“中国规范”大;但对于群桩基础的地震需求, 当桥墩屈服后, 基本相同;基础的转角不控制设计。
参考文献
CJJ166-2011, 城市桥梁抗震设计规范 [S]. ↩
社团法人,道路桥示方书(V 耐震设计篇)・同解说 [S]. 东京:日本道路桥协会,2011. ↩
社团法人,道路桥示方书(I 共通篇・ IV 下部构造篇)・同解说 [S]. 东京:日本道路桥协会,2011. ↩
叶爱君. 桥梁抗震 (第二版)[M]. 北京:人民交通出版社,2011.
孙利民,范立础. 版神地震后日本桥梁抗震设计规范的改订 [J]. 同济大学学报,2001,29(1):60-64. ↩
崔晨,张磊,吴军伟,等. 桥梁预制装配的 BIM 施工管理平台设计 [J]. 土木建筑工程信息技术,2016,8(6):51-54.
沈维芳,卢永成. 上海中环线国定东路下匝道预制装配桥梁技术 [J]. 城市道桥与防洪,2017(9):68-73.
崔晨,陆小青.BIM 技术在 S20 公路入城段(G15- 嘉闵高架路)桥梁工程中的应用 [J]. 上海建设科技,2018(3):16-19.
刘亮,李利宾,束新宇,等.BIM 技术在装配式钢 - 混凝土组合箱梁桥施工中的应用 [J]. 钢结构,2018,33(6):119-122,127.