吴勇^1, 陈方有^2, 朱家豪^2
(^1上海市城市建设设计研究总院 (集团) 有限公司,上海 200125;^2同济大学土木工程防灾国家重点实验室, 上海 200092)
摘要:为研究斜拉桥横向减震体系的减震行为,以一座高低塔曲线斜拉桥为工程背景,结合桥梁新型横向钢阻尼器,给出了可行的斜拉桥全桥横向减震体系的优化设计方法,并与横向固定体系进行比较,分析了其减震效果。研究表明:地震作用下,斜拉桥横向减震体系能显著减小桥墩及其基础的地震需求,亦能一定程度上减小桥塔及其基础的地震需求,同时,将主梁的地震位移控制在合理范围内;钢阻尼器的滞回耗能能力明显优于摩擦型支座。
关键词:斜拉桥;横向钢阻尼器;横向减震体系
0 引言
随着我国桥梁建设水平的不断提升,斜拉桥的建设越来越多,斜拉桥在地震作用下,主梁惯性力主要通过斜拉索以及塔 - 梁、墩 - 梁间连接传递给桥塔和桥墩再传至基础。因此,斜拉桥的地震反应及抗震性能与其结构体系密切相关。对于纵桥向,常采用飘浮体系或半飘浮体系,且可在塔 - 梁连接处配以黏滞阻尼器控制主梁纵向位移,因此主塔的纵向抗震性能比较好1,2;对于横桥向,墩 - 梁间常采用的固定约束方式往往容易影响桥梁下部结构尤其是基础控制设计。国内抗震设计规范3,4要求,斜拉桥主塔及基础在设防地震下须保持弹性,并对桥塔及基础进行强度验算。为满足斜拉桥横向抗震要求,常将桥塔、基础等部件设计得具有足够的能力以抵抗设防地震,这将大大增加工程造价。因此,有必要给出合理的斜拉桥横向减震体系及设计方法以指导工程设计。
目前,国内外学者对大跨度斜拉桥的横向减震体系进行了一定的研究。叶爱君等5以苏通大桥为例,对边墩与主梁的合理约束体系进行了研究,指出了墩梁间横向设置黏滞阻尼器可以有效地减小边墩横向内力和梁端位移,同时指出斜拉桥横向全漂浮体系不是合理的抗震体系;管仲国等6,7对由斜拉桥弹塑性索和黏滞阻尼器组成的减震系统进行了研究,并指出该组合系统可大幅降低主塔塔底弯矩及主梁加速度响应;希腊 Rion-Antirion 桥8塔梁、墩梁横向采用由黏滞阻尼器和牺牲性连杆组成的减震系统,以适应强震作用和断层位移;沈星等9,10,11,12,13发明了一种新型桥梁横向钢阻尼器,提出了斜拉桥边墩横向新型钢阻尼器减震体系,并指出该体系能有效地减小桥墩及其基础的地震内力和墩梁相对位移。
由于本文所研究的高低塔曲线斜拉桥结构复杂,且桥址处于高烈度区,若采用横向固定体系,桥梁下部结构会控制抗震设计,若仅在边墩处设置新型横向钢阻尼器11仍无法满足桥塔及其基础的抗震要求,需将钢阻尼器布置于桥墩墩顶和桥塔横梁处。因此,需要对该减震体系力学参数进行合理优化并给出对应设计方法,同时,对高低塔曲线斜拉桥横向钢阻尼器减震体系的抗震效果作进一步研究。为此,本文以柴家峡大桥为背景,给出斜拉桥全桥横向减震体系的优化设计方法,最后与横向固定体系对比,分析斜拉桥横向减震体系的减震效果。
1 工程背景
1.1 工程概况
本文以柴家峡黄河大桥为工程背景。该桥主桥为 6 跨高低塔双索面曲线斜拉桥,主跨跨径 364 \text{m},跨径布置为 46.8 \text{m} + 49.2 \text{m} + 364.0 \text{m} + 49.20 \text{m} + 46.80 \text{m} + 42.862 \text{m},如图 1 所示。由于黄河特殊地貌环境的限制,展现空间非常紧张,因此南岸边跨和主跨范围进入曲线段,曲线半径仅 600 \text{m}。主桥平面示意图如图 2 所示。主梁采用双主梁钢箱梁作为标准截面;主塔为钻石型混凝土桥塔,其中,南塔总高度为 99.9 \text{m},北塔总高度为 115.5 \text{m};主桥基础采用群桩基础,为钻孔灌注桩并按嵌岩桩设计,主塔桩基桩径为 2.5 \text{m},过渡墩和辅助墩桩基桩径为 1.5 \text{m}。
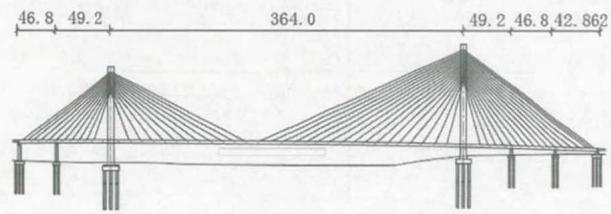
图 1 主桥立面(\text{m})

图 2 主桥平面(\text{m})
1.2 地震动输入
本文地震动输入采用由该桥 E2 设计反应谱拟合的 7 条人工时程波,计算结果取 7 条波计算结果的平均值。另外,考虑了最不利输入方向的影响,最终结果选取横向 + 竖向和南辅助墩径向 + 竖向作为输入方向,计算结果取上述两个输入方向的大值。图 3 为其中一条人工时程波图示。7 条波的峰值均调到 0.4g,且竖向地震动采用水平地震动输入值的 0.65 倍。图 4 所示为人工时程反应谱与规范反应谱对比。
图 3 地震动输入(7 条中的一条)
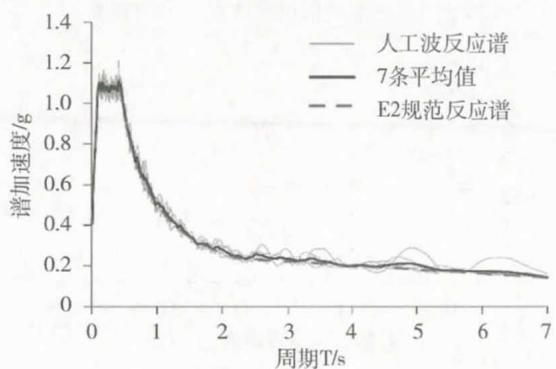
图 4 人工时程反应谱与规范反应谱比较
2 斜拉桥横向减震体系优化设计
2.1 横向钢阻尼器及减震体系简介
横向钢阻尼器构造如图 5 所示,由上、下两部分组成。上半部分用螺栓连接于梁底,由上顶板和设置了聚四氟乙烯滑板的钢挡板组成;下半部分用螺栓连接于墩顶或桥塔横梁上,由底板、焊接在底板上的三角形钢板以及半球型传力键组成;上下两部分通过半球形传力键与上顶板钢挡块两侧的聚四氟乙烯板接触连接,能够很好适应桥梁纵向较大的位移变形,同时,采用球形传力键能更好地适应地震下复杂的接触条件。该钢阻尼器以三角形钢板为耗能构件,具有较好的耗能能力。地震时,上部结构惯性力由钢挡板经三角钢板顶点的球形传力键传递给三角形钢板,三角钢板在面外水平地震作用下沿高度范围内全截面屈服耗能。钢阻尼器的力学特性可采用双线性模型模拟,力 - 位移曲线如图 6 所示,主要力学参数为阻尼器屈服力 F_{\text{eff}}、弹性刚度 K_y、屈后刚度 K_h,极限位移能力 D_u,上述参数的确定方法可参见文献9,14。
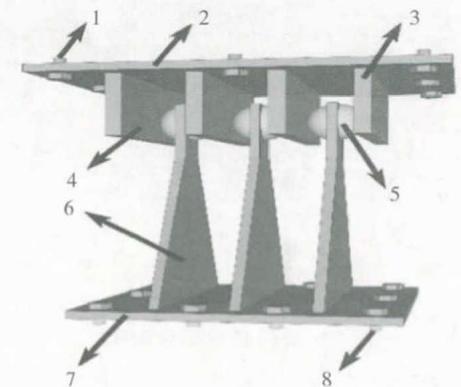
图 5 横向钢阻尼器构造示意
1 为上顶板螺栓,2 为上顶板,3 为上顶板挡板,4 为聚四氟乙烯滑片,5 为半球形钢传力键,6 为三角形钢板,7 为下底板,8 为下底板螺栓
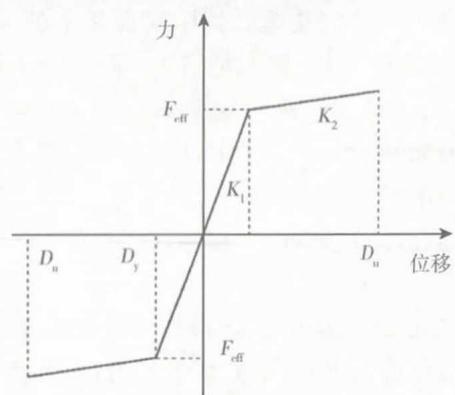
图 6 横向钢阻尼器本构图
为减小桥墩、桥塔及其基础的横向地震需求,可将上述新型横向钢阻尼器与球钢支座并联放置于桥墩和桥塔横梁处,考虑背景桥梁边跨跨度较小,钢阻尼器仅布置与过渡墩和桥塔处,辅助墩处未布置钢阻尼器。横向地震作用下,球钢支座的横向限位销被剪断,变为滑动型支座提供竖向支承,利用钢阻尼器屈服耗能,并延长结构周期,以减小桥梁横向地震力反应,同时限制连接相对位移,依靠钢阻尼器屈后刚度减小其震后残余位移。球钢支座横向限位销的剪断力满足桥梁正常使用即可,通常取支座吨位的 10\%,但须小于与之并联的钢阻尼器屈服力。
2.2 桥梁动力计算模型
采用 SAP2000 建立了三维有限元模型进行了地震反应分析,全桥模型如图 7 所示。主梁、桥墩和桥塔采用框架单元模拟,拉索采用框架单元模拟并释放杆端弯矩和扭矩;桥塔、主梁、桥墩及拉索均考虑恒载轴力对几何刚度影响,并考虑拉索垂度效应。各主塔、桥墩基础采用六弹簧模拟,基础刚度由“m 法”确定。
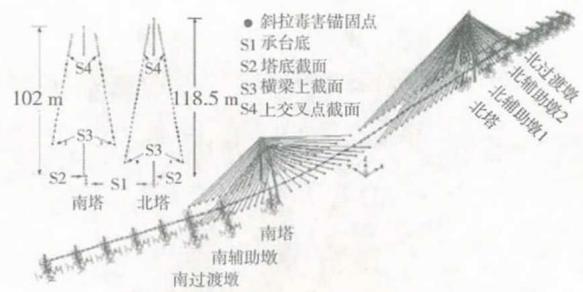
图 7 斜拉桥模型示意图
本文采用了横向固定和横向减震两种边界连接条件,为便于表述,将两种边界连接条件体系所对应的体系分别简称为横向固定体系和横向减震体系。对于横向固定体系,在纵桥向支座可自由活动,而墩梁、塔梁横向固定,竖向采用大刚度模拟支座竖向支承;横向减震体系则为滑动型球钢支座和钢阻尼器组成的减震体系边界,布置于南、北过渡墩和桥塔处,采用 PlasticWen 单元模拟;滑动型球钢支座采用 PlasticWen 单元模拟,其恢复力模型如图 8 所示。图中,F_{\max} 为临界摩擦力,X 为上部结构与墩顶的相对位移,x_y 为临界位移。弹性恢复力最大值与临界滑动摩擦力相等,即
上式中:f 为滑动摩擦因数,边墩与主塔处球形钢支座的滑动摩擦因数取为 2\%;N 为支座反力;临界位移 x_y 取 2 \text{mm}。
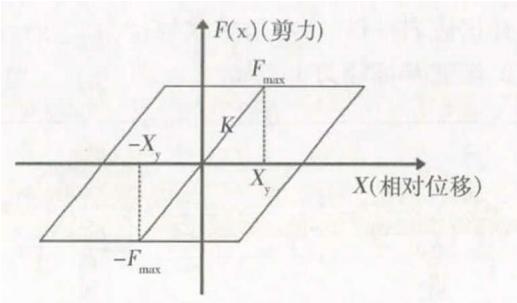
图 8 滑动支座恢复力模型
2.3 横向减震体系力学参数优化
斜拉桥横向减震体系设计是一个不断优化的过程,可按下述过程进行阻尼器屈服力优化:①确定地震下容许的墩梁、塔梁相对位移;②桥墩处支座均设置为横向活动支座,去除桥塔抗风支座,进行桥塔处阻尼器屈服力优化,根据塔梁相对位移与阻尼器屈服力的关系,初步选定桥塔处阻尼器屈服力;③在②的基础上进行桥墩处阻尼器屈服力优化,确定阻尼器屈服力;④将上述优化后的阻尼器力学参数,代入全桥计算模型,检算连接位移、结构强度是否满足要求,如若不满足,继续优化阻尼器屈服力。当减震体系的墩梁、塔梁位移满足目标位移而结构强度不满足抗震要求时,需考虑加大截面尺寸和配筋。
在进行阻尼器屈服力的优化时,钢阻尼器硬化率对连接相对位移、结构地震力影响很小,可暂取 5\%。另外,弹性刚度 K_y 与屈服力的比(记为 K)为屈服位移的倒数,即 K = E \times t / (\sigma_y \times H^2),阻尼器弹性刚度和屈服力与过渡墩、墩梁连接位移以及地震力的关系见图 9、图 10。结果表明,增大阻尼器的屈服力能显著减小墩梁连接相对位移,但不会显著增大桥墩的地震力;另外,系数 K 对连接相对位移、结构地震力的影响很小,因此,在进行阻尼器屈服力优化过程中,可根据阻尼器的安装空间和钢材等级预估比例系数 K。
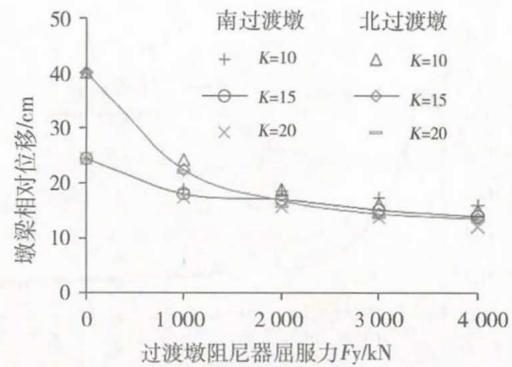
图 9 墩梁相对位移与阻尼器屈服力关系
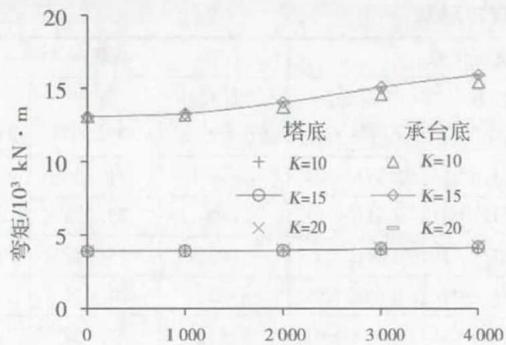
图 10 北过渡墩关键截面弯矩与阻尼器屈服力关系
下面以柴家峡大桥为例,说明斜拉桥横向减震体系力学参数优化设计过程,优化目标为将连接的相对位移控制在 0.3 \text{m} 以内。图 11、图 12 为桥塔和桥墩处阻尼器屈服力与其相对位移的关系,从图中结果可以看出,随着全桥横向阻尼器屈服力等幅增加,各连接相对位移均显著减小,且当阻尼器屈服力取为 8000 \text{kN} 时,塔梁相对位移满足优化要求。随后,将桥塔处阻尼器屈服力取为 8000 \text{kN},继续对桥墩处阻尼器进行优化,随着各桥墩处阻尼器屈服力等幅增加,墩梁相对位移显著减小,南塔塔梁相对位移缓慢减小,北塔塔梁相对位移基本不变。此外,从图中结果可以看出,斜拉桥南北侧的相对位移变化幅度呈非对称关系。为使其相对位移变化幅度趋于对称,各桥塔和桥墩阻尼器屈服力须取不同值。结合地震下容许的主梁目标位移,经过试算调整,确定南过渡墩、南塔、北塔和北过渡墩处阻尼器屈服力分别为 2000, 7000, 8000 和 3000 \text{kN}。
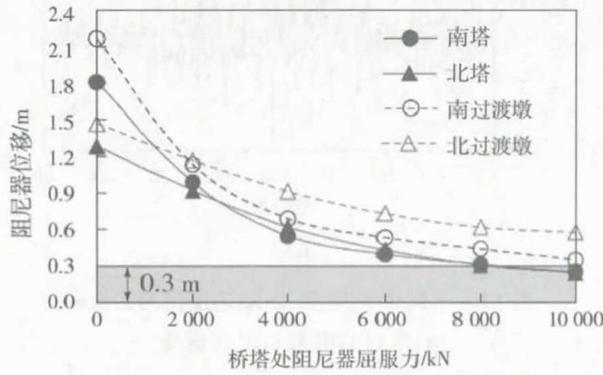
图 11 连接位移与桥塔处阻尼器屈服力关系
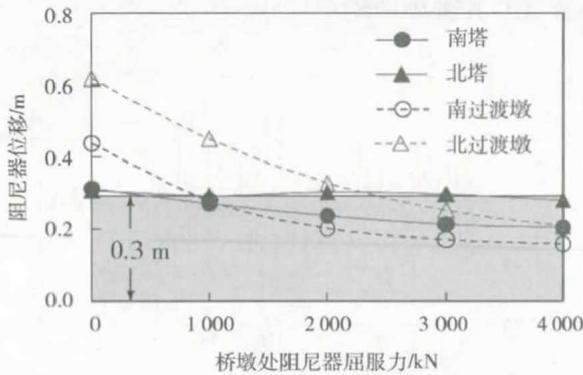
图 12 连接位移与桥墩处阻尼器屈服力关系
2.4 阻尼器选型与布置
根据阻尼器的地震位移需求、屈服力以及实际的安装空间,选定三角钢板的钢材等级为 Q500;三角形钢板的板高 H 为 80 \text{cm},板宽 B 为 100 \text{cm},板厚 t 为 3 \text{cm}。每组钢阻尼器采用 8 块三角形钢板,其中,南过渡墩布置 2 组,南塔布置 7 组,北塔布置 8 组,北过渡墩布置 3 组。
采用 Abaqus 软件,确定选型后阻尼器的力学参数,其中,南过渡墩、北过渡墩、南塔和北塔处钢阻尼器的总屈服力分别为 1936, 2904, 6776 和 7744 \text{kN};弹性刚度分别为 28960, 43440, 101360 和 115840 \text{kN/m};阻尼器的位移能力为 33 \text{cm},硬化率为 0.121。将选型后的阻尼器力学参数重新代入有限元模型中计算,检算各连接位移,此时,从南过渡墩到北过渡墩,各连接相对位移分别为 20, 23, 25, 27, 25, 23 和 22 \text{cm},连接位移满足目标位移要求,且结构抗震性能满足设防要求。
3 减震效果分析
表 1 给出了斜拉桥横向固定体系和横向减震体系关键截面地震力的比较。从表中结果可以看出,在 E2 设防地震作用下,与固定体系相比,①减震体系能显著减小桥墩墩底及承台底的剪力和弯矩需求。由于 E2 地震作用下,桥墩处预先设计的支座横向固定销被剪断,形成滑动型球钢支座和钢阻尼器组成的减震体系减震耗能。对于辅助墩而言,由于地震下主梁传递给桥墩的惯性力为支座摩擦力,因此墩底和承台底弯矩、剪力显著减小,其中承台底弯矩最大减小了 90.2\%;对于设置钢阻尼器的南、北过渡墩而言,地震下主梁传给桥墩的惯性力为阻尼器的屈服力和支座摩擦力,因此也显著减小了桥墩及其基础的地震需求,其中,南北过渡墩承台底弯矩分别减小了 74.1\% 和 64.4\%。同时,钢阻尼器起到了很好的滞回耗能及限位作用。②减震体系的桥塔塔底及承台底的弯矩和剪力均有一定程度的减小。
表 1 固定体系与减震体系地震力对比
| 横向固定体系 | 横向减震体系 | 减震率 | |
|---|---|---|---|
| 位置 | 轴力 A/\text{kN} | 剪力 B/\text{kN} | 弯矩 C/(\text{kN} \cdot \text{m}) |
| 南过渡墩底 | 1.20 \text{E}+04 | 1.51 \text{E}+04 | 1.70 \text{E}+05 |
| 南辅助墩底 | 1.21 \text{E}+04 | 5.38 \text{E}+03 | 7.24 \text{E}+04 |
| 南塔塔底 | 1.02 \text{E}+05 | 8.34 \text{E}+04 | 3.64 \text{E}+06 |
| 北塔塔底 | 1.06 \text{E}+05 | 1.04 \text{E}+05 | 3.76 \text{E}+06 |
| 北辅助墩1墩底 | 1.02 \text{E}+04 | 1.01 \text{E}+04 | 6.24 \text{E}+04 |
| 北辅助墩2底 | 1.13 \text{E}+04 | 1.48 \text{E}+04 | 7.10 \text{E}+04 |
| 北过渡墩底 | 8.33 \text{E}+03 | 1.21 \text{E}+04 | 1.02 \text{E}+04 |
| 南过渡墩承台底 | 1.44 \text{E}+04 | 1.75 \text{E}+04 | 2.16 \text{E}+05 |
| 南辅助墩承台底 | 1.31 \text{E}+04 | 8.08 \text{E}+03 | 8.42 \text{E}+04 |
| 南塔承台底 | 1.36 \text{E}+05 | 1.19 \text{E}+05 | 3.90 \text{E}+06 |
| 北塔承台底 | 1.37 \text{E}+05 | 1.34 \text{E}+05 | 4.12 \text{E}+06 |
| 北辅助墩1承台底 | 1.11 \text{E}+04 | 1.19 \text{E}+04 | 8.98 \text{E}+04 |
| 北辅助墩2承台底 | 1.28 \text{E}+04 | 1.70 \text{E}+04 | 1.11 \text{E}+05 |
| 北过渡墩承台底 | 1.09 \text{E}+04 | 1.50 \text{E}+04 | 5.05 \text{E}+04 |
注:表中截面位置见图 5
图 13 为横向地震作用下固定体系与减震体系的主梁加速度比较,图 14 为固定体系和减震体系墩梁、塔梁连接传力比较。从图示结果可以看出:在地震作用下,与固定体系相比,减震体系能显著减小主梁的加速度峰值,所以减震体系能显著降低由主梁传递给桥塔和桥墩的惯性力,进而可减小桥墩 (塔) 及其基础的地震需求;另外,横向减震体系主梁横向加速度沿主梁长度方向变化很小。
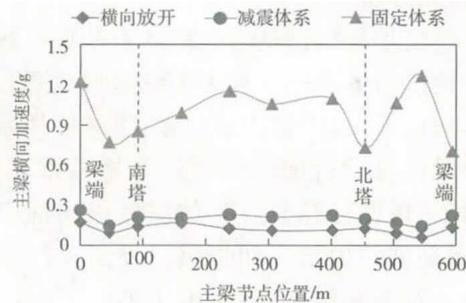
图 13 不同横向结构体系主梁加速度对比
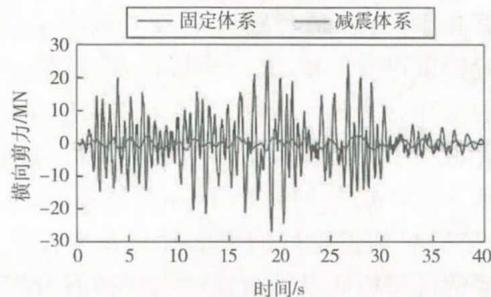
(a) 南过渡墩处
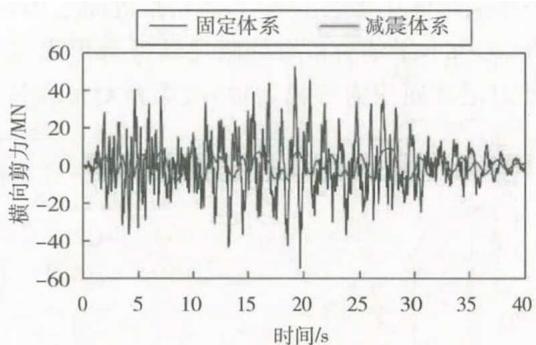
(b) 南塔处
图 14 不同体系墩梁、塔梁连接传力比较:
图 15、图 16 分别为不同体系南过渡墩处墩底剪力和弯矩比较,从图示结果可以看出,减震体系能显著减小桥墩及其基础的地震需求。
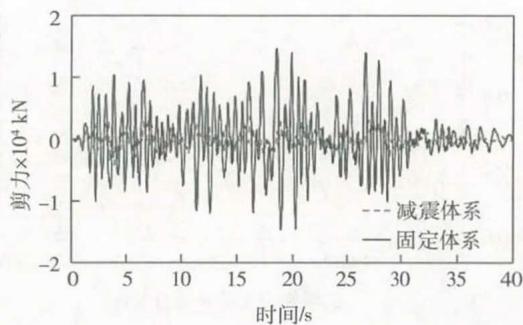
图 15 不同体系南过渡墩墩底横向剪力比较
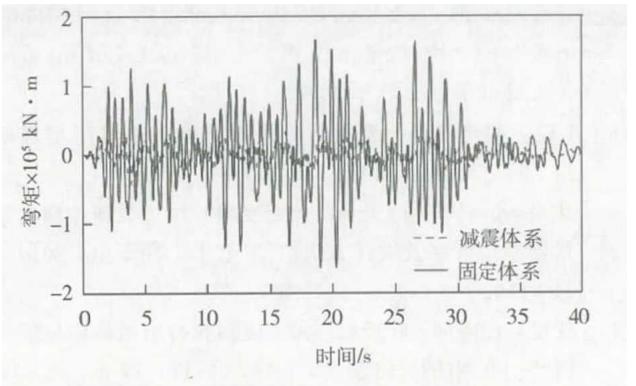
图 16 不同体系南过渡墩墩底横向弯矩比较
图 17 为横向地震作用下固定体系与减震体系的主梁跨中横向位移时程比较,从图 17 可以得出减震体系主梁呈现出低频振荡的特点,从而减小了主梁的加速度以及主梁传递给桥墩和桥塔的地震力。
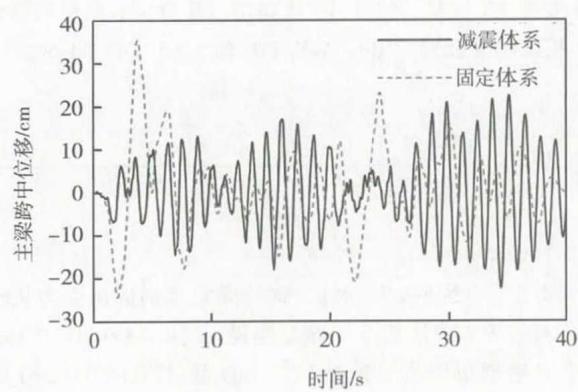
图 17 不同横向结构体系主梁跨中位移时程对比
图 18、图 19 给出了横向地震作用下减震体系过渡墩和辅助墩阻尼器位移时程,结果表明减震体系墩 - 梁、塔 - 梁横向相对位移得到了较好的控制。
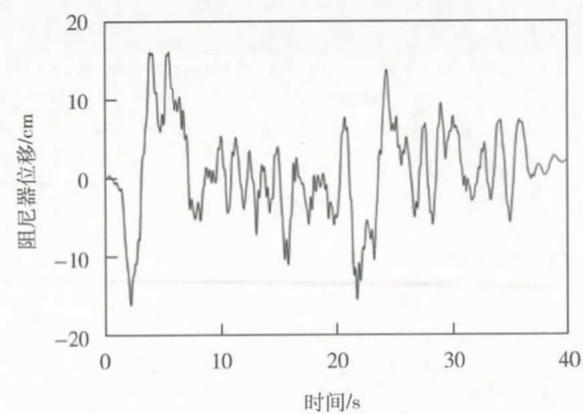
图 18 南辅助墩阻尼器位移时程
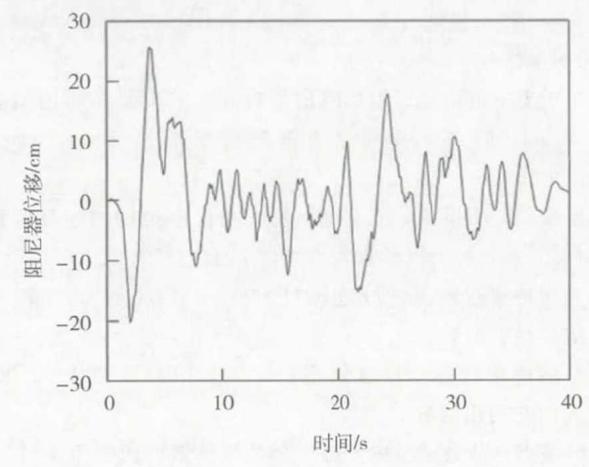
图 19 南塔阻尼器位移时程
图 20 所示为南塔处钢阻尼器和球钢支座的耗能时程比较(一条时程结果),从图示结果可以看出,与支座摩擦耗能相比,钢阻尼器耗能能力非常优异。
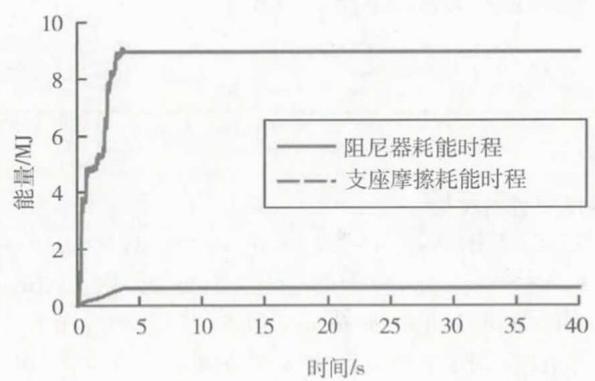
图 20 钢阻尼器和摩擦支座耗能时程比较
4 结语
(1) 本文所给的斜拉桥全桥减震体系优化设计方法可行;由于结构的非对称性,减震体系中钢阻尼器屈服力在各连接节点间的分配也是非对称的。
(2) 与固定体系相比,地震作用下,斜拉桥横向减震体系能显著减小主梁加速度,从而减小了主梁传递给桥墩和桥塔的惯性力,因此,能显著减小桥墩及其基础的地震需求,亦能一定程度上减小桥塔及其基础的地震需求,同时将主梁位移限制在合理范围内。
(3) 钢阻尼器的耗能能力明显优于摩擦型支座。
参考文献
叶爱君, 范立础. 附加阻尼器对超大跨度斜拉桥的减震效果 [J]. 同济大学学报(自然科学版), 2006, 34(7): 859-863. ↩
叶爱君, 胡世德, 范立础. 超大跨度斜拉桥的地震位移控制 [J]. 土木工程学报, 2004, 37(12):38-43. ↩
城市桥梁抗震设计规范: CJJ 166-2011[S]. 北京: 中国工业出版社, 2011. ↩
公路桥梁抗震设计细则:JTG/T B02-01—2008[S]. 北京:人民交通出版社,2008. ↩
叶爱君, 范立础. 超大跨度斜拉桥的横向约束体系 [J]. 中国公路学报, 2007, 20(2):63-67. ↩
游瀚, 管仲国. 弹塑性索和黏滞阻尼器系统用于斜拉桥横向减震分析 [J]. 振动与冲击,2017,36(14):183-188. ↩
Guan Z, You H, Li J Z. Lateral Isolation System of a Long-Span Cable-Stayed Bridge with Heavyweight Concrete Girder in a High Seismic Region[J]. Journal of Bridge Engineering, 2016, 22(1):04016104. ↩
Castellano M G, Infanti S, Papanikolas P, et al. Rion antirion bridge; design and full - scale testing of the seismic protection devices[J]. 2004. ↩
沈星, 倪晓博, 叶爱君. 桥梁新型横向金属阻尼器研究 [J]. 振动与冲击, 2014, 33(21):96-101. ↩ ↩
沈星, 倪晓博, 叶爱君. 大跨度斜拉桥边墩新型横向钢阻尼器减震体系及设计方法 [J]. 土木工程学报, 2016(5): 110-119. ↩
沈星, 倪晓博, 叶爱君. 大跨度斜拉桥边墩横向抗震体系研究 [J]. 中国公路学报, 2016, 29(11):82-89. ↩ ↩
Shen X, Camara A, Ye A. Effects of seismic devices on transverse responses of piers in the Sutong Bridge[J]. Earthquake Engineering & Engineering Vibration, 2015, 14(4):611-623. ↩
Shen X, Wang X, Ye Q, et al. Seismic performance of Transverse Steel Damper seismic system for long span-bridges[J]. Engineering Structures, 2017, 141:14-28. ↩
刘腾飞, 沈星, 叶爱君. 桥梁用三角形钢板阻尼器恢复力模型的参数确定 [J]. 结构工程师,2014(6):54-60. ↩