倪晓博,李闽,叶爱君
(同济大学土木工程防灾国家重点实验室 上海市 200092)
摘要:针对一座规则连续梁桥,采用延性抗震设计策略,分别基于《城市桥梁抗震设计规范》与《公路桥梁抗震设计细则》,进行了全面地地震反应分析和抗震验算,并着重对两本规范的设计反应谱及产生的地震反应、抗震验算指标的计算结果进行了详细地对比分析。结果表明,前者较大的反应谱参数对延性构件的强度和位移能力提出了较大的要求,对于能力保护构件,后者在构件能力计算方面偏于保守,对构件能力提出了更高要求。
关键词:桥梁抗震;规范;比较;延性;算例
1 规范概况
近几年来,我国《公路桥梁抗震设计细则》(JTG/T B02-01—2008)(以下简称《公规》)、以及《城市桥梁抗震设计规范》(CJJ 166—2011)(以下简称《城规》)先后编制出版,并开始实施。这两本规范引入了新的桥梁抗震设计理念,完善了相应的抗震设计方法,所以随着这两本规范的实施,我国的桥梁抗震设计水平将会上一个台阶。
两本规范均采用两水准设防、两阶段设计的抗震设计方法。在具体操作中,根据桥梁的重要性和在抗震救灾中起的作用,把桥梁进行分类,并对各类桥梁进行复杂程度不同的抗震设计。《城规》按照结构形式、在城市交通网络中位置的重要性及承担的交通量分为甲至丁四类,《公规》根据公路等级及桥梁的重要性和修复(抢修)的难易程度分 A 至 D 类。对于每一类桥梁,两本规范均给出了明确的抗震设防标准,即两个设防地震水准(地震动参数)以及对应的抗震性能目标,虽然两本规范的桥梁类别划分原则不同,但针对量大面广的乙 (B) 类和丁 (C) 类桥梁(以下简称“常规桥梁”)两本规范的抗震设防标准基本是一致的。
对于常规桥梁采用延性抗震设计和减隔震设计两种策略,在地震反应分析和抗震验算方法方面也基本相同。对于地震反应分析,均采用以反应谱方法为主,少量情况进行时程反应分析的方法;只是《城规》中反应谱方法的适用范围更广一些。对于延性抗震设计,均采用能力设计方法,验算延性构件(桥墩的强度和变形能力),验算能力保护构件的强度(桥墩抗剪、固定支座、盖梁、桩基础等)。
两本规范的最大不同点,是由于规范的主管部门不同,采用了不同的地震动参数。同时,在桥墩和桩基础的抗震能力计算公式方面,也有一些不同的规定。
在桥梁的延性设计中,主要需要验算延性构件(墩柱)的抗震能力,以及能力保护构件(固定支座、桩基础等)的抗震能力。下一节将针对一座实际的连续梁桥,同时根据两本规范进行延性抗震设计,在地震动输入比较的基础上,着重对桥墩、桩基础和支座的抗震需求和能力进行详细比较,以定量分析两本规范的不同地震动参数和部分抗震能力计算公式,对常规桥梁抗震设计所产生的影响,供设计人员参考。
2 延性抗震设计比较
2.1 结构概况
某城市高架连续梁桥,一联 (4\times 31\mathrm{m}),属于规范规定的规则桥。纵桥向,中墩为纵向固定墩,墩顶设纵向固定支座,其他墩设纵向活动墩,墩顶设纵向滑动支座;横桥向,各墩顶均在中间两片箱梁下设置横向固定盆式支座,其余位置均设横向活动盆式支座。每跨上部结构总质量为 1590.8\mathrm{t} (包括二期恒载)。
桥梁横断面与基础布置如图 1 所示。盖梁为矩形截面,平均高度 3.2\mathrm{m},支座和垫石总高 0.3\mathrm{m}。
立柱中心间距 7\mathrm{m},墩柱高度 15\mathrm{m}、截面尺寸为 1.8\mathrm{m} (横桥向) \times 2.0\mathrm{m} (纵桥向),桩基采用 20 根 \phi 800~\mathrm{mm} 钻孔灌注桩(摩擦桩),桩长 50~\mathrm{m},单桩配筋率 20%,单桩承载力 2500\mathrm{kN},场地土系数 m 值为 10000\mathrm{kN / m^4}。主梁、立柱、基础分别采用 C50、C40、C35 混凝土。盖梁质量 481\mathrm{t},两根立柱质量为 281\mathrm{t},承台质量为 493.8\mathrm{t}。
计算得到桥梁结构对的动力特性:纵桥向基本周期,E1 地震下 3.23s,E2 地震下 4.83s;横桥向基本周期,E1 地震下 1.06s,E2 地震下 1.36s。
(a) 横断面
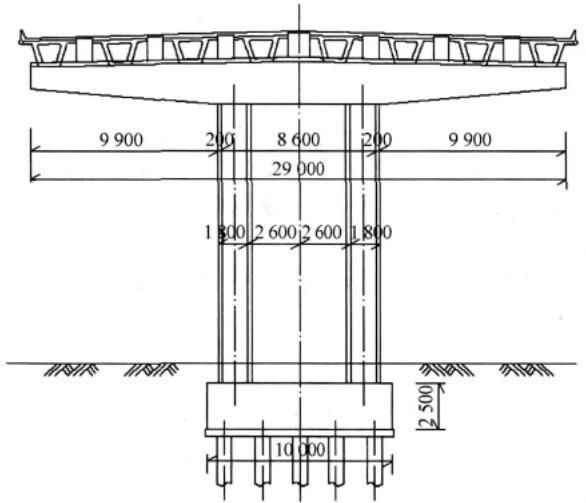
单位:mm
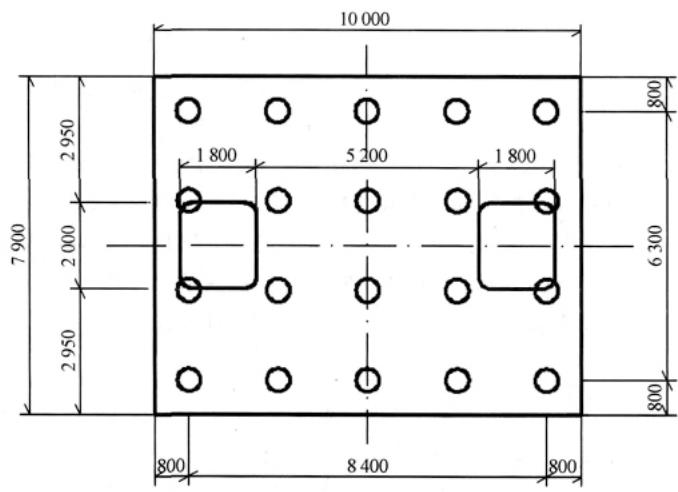
(b) 基础布置
图 1 桥梁横断面与基础布置
2.2 地震动输入比较
通过《中国地震动参数区划图》查得,桥梁所在场地的设计基本地震加速度峰值为 0.1\mathrm{g},抗震设防烈度 7 度,地震分区第一区,场地类型四类场地,反应谱特征周期为 0.65\mathrm{s}。
按照《公规》,桥梁类别为 B 类,E1 地震下抗震重要性系数 C_i 为 0.43,场地系数 C_s 为 1.4,桥梁阻尼比为 0.05,故阻尼调整系数 C_d 为 1.0;E2 地震下抗震重要性系数 C_i 为 1.3,场地系数 C_s 为 1.4,阻尼调整系数 C_d 为 1.0。而按照《城规》,桥梁类别为乙类,E1 地震下地震调整系数 C_i 为 0.61;E2 地震下地震调整系数 C_i 为 2.2。
依据上述参数,图 2 比较了两规范在 E1 和 E2 地震下的加速度反应谱,并注明了本桥梁在两设防水准下纵桥向和横桥向结构自振周期。
由图 2 可知,就加速度反应谱而言:(1)《城规》反应谱周期到6\mathrm{s}截止,《公规》反应谱到 10\mathrm{~s} 截止;(2)相同条件下,《城规》与《公规》的反应谱平台宽度相同,E1 地震下《城规》与《公规》反应谱平台高度相近,E2 地震下《城规》反应谱平台高度明显大于《公规》反应谱平台高度;(3)无论是 E1 地震还是 E2 地震下,《城规》反应谱取值始终比《公规》反应谱大,而且 E2 地震下大的程度更多;(4)在 E1 地震下,桥梁
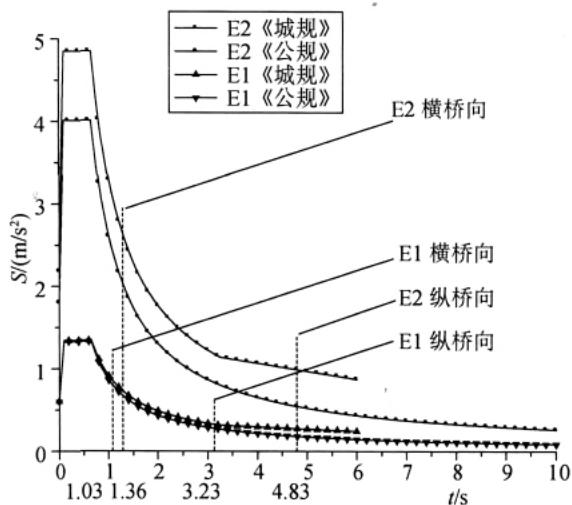
图 2 水平加速度反应谱比较
的纵、横向基本周期对应的反应谱值,《城规》分别为《公规》的 1.19 和 1.06 倍,在 E2 地震下,桥梁的纵、横向基本周期对应的反应谱值,《城规》分别为《公规》的 1.83 和 1.3 倍。
2.3 墩柱的抗震验算比较
在延性抗震设计中,常规桥梁的墩柱往往按延性构件设计,需要进行 E1 地震下的抗弯强度验算和 E2 地震下的变形能力验算,并采用能力设计方法进行抗剪验算。
2.3.1 E1地震下的墩柱抗弯强度验算比较
表 1 列出了在 E1 地震下,按两本规范进行的墩柱抗弯强度验算结果,并进行了比较。由表中结果可见,两本规范设计反应谱值的不同,导致了按《城规》计算的弯矩需求比按《公规》计算的弯矩需求稍大,而抗弯能力是相同。
表 1 E1 地震下墩柱抗弯强度验算
| 计算项目 | 纵桥向 | 横桥向 | ||||
|---|---|---|---|---|---|---|
| 城规 | 公规 | 比值 | 城规 | 公规 | 比值 | |
| 反应谱值/(m/s2) | 0.318 | 0.268 | 1.187 | 0.888 | 0.839 | 1.058 |
| 水平地震力/kN | 1247 | 901 | 1.384 | 1983 | 1874 | 1.058 |
| 弯矩需求/(kN·m) | 11531 | 8330 | 1.384 | 10396 | 10010 | 1.039 |
| 抗弯能力/(kN·m) | 11535 | 11535 | 1.000 | 14510 | 14510 | 1.000 |
2.3.2 E2地震下的墩柱变形能力验算比较
表 2 列出了在 E2 地震下,按两本规范进行的桥墩位移能力验算结果,并进行了比较。
表 2 E2 地震下墩柱位移能力验算
| 计算项目 | 纵桥向 | 横桥向 | ||||
|---|---|---|---|---|---|---|
| 城规 | 公规 | 比值 | 城规 | 公规 | 比值 | |
| 反应谱值/(m/s2) | 0.99 | 0.54 | 1.833 | 2.5 | 1.92 | 1.302 |
| 水平地震力/kN | 5897 | 2783 | 2.119 | 5583 | 4288 | 1.302 |
| 位移需求/m | 0.504 | 0.238 | 2.119 | 0.117 | 0.089 | 1.302 |
| 位移能力/m | 0.971 | 0.742 | 1.309 | 0.368 | 0.368 | 1.000 |
对于规则桥梁,两本规范在确定位移需求时,都是将延性构件的截面改为等效刚度后,采用反应谱方法计算弹性位移,然后进行修正作为弹塑性位移。但是两本规范中修正系数 R_{d} 的计算公式有所不同。
《城规》 R_{d} 计算公式:
《公规》 R_{d} 计算公式:
式中: \mu_d 为桥墩构件延性系数,一般可取 3; T_g 为反应谱特征周期。
可见,对于长周期结构,两本规范均采用等位移准则,但对长周期的定义有所不同,《公规》为 T_{g},《城规》为 1.25T_{g};而对于中短周期结构,按《城规》计算的结果将比按《公规》计算值大。E2 地震下,本文桥梁的纵、横向结构自振周期分别为 4.83\mathrm{s} 和 3.23\mathrm{s},均属于长周期范围,位移修正系数 R_{d} 取 1。两本规范的位移需求可以直接取弹性位移,按反应谱方法计算,由于设计反应谱的差别,最终得到的纵、横向位移需求,《城规》分别是《公规》的 2.12 和 1.30 倍。
另一方面,在两本规范中,桥墩的位移能力均是根据塑性铰区的允许塑性转角计算的,而允许塑性转角又取决于截面的允许塑性曲率和等效塑性较长度。除了等效塑性铰长度计算公式外,两本规范的位移能力计算公式是一致的。《公规》等效塑性铰长度计算公式中还考虑了截面尺寸的限制,这样可能得到较小的等效塑性铰长度。对于本文桥梁,《城规》等效塑性铰长度 I_{p} = 172\mathrm{cm},《公规》等效塑性铰长度 I_{p} = 120~\mathrm{cm},最终计算的位移能力《城规》 97.1\mathrm{cm},《公规》 74.2\mathrm{cm},可见按《城规》将得到较大的位移能力。
2.3.3 墩柱的抗剪能力验算比较
对于按延性抗震设计的桥梁,在 E2 地震作用下墩柱屈服后,要按能力保护原则计算墩柱的剪力需求,与地震输入无关,因此两规范将得到相同的结果。
而在墩柱的抗剪能力计算方面,《公规》与《城规》均给出了墩柱塑性铰区抗剪能力计算公式,而且都引入了美国抗震设计规范推荐的计算公式,但均未规定塑性铰区以外的抗剪强度计算公式。《公规》采用了 Caltrans 的抗剪计算公式,但对混凝土提供的抗剪能力计算公式进行了非常保守的简化,取最小残余能力,而且忽略轴压力的贡献6,7。《城规》采用 AASHTO 的抗剪计算公式,根据墩柱的延性水平计算混凝土的贡献,考并虑了轴压力的贡献。
表 3 列出了分别按两本规范计算的墩柱塑性铰区抗剪强度具体数值。表中结果表明,《城规》考虑混凝土抗剪能力贡献大约是《公路》的 10 倍,《公规》对于混凝土抗剪能力贡献过于保守。两本规范对钢筋提供的抗剪能力相同,最终总的抗剪能力《城规》是《公规》的 2 倍。
2.4 桩基础的抗震验算比较
两本规范均规定,在延性设计中,桩基础按能力保护构件设计,进行强度验算。《公规》规定,按《公路桥涵地基与基础设计规范》(JTG D63-2007)进行基础强度验算。而《城规》则规定,在《公路桥涵地基与基础设计规范》的基础上,非液化土中,单桩的
表 3 墩柱塑性铰区截面抗剪强度比较
| 规范 | 纵桥向/kN | 横桥向/kN | ||||
|---|---|---|---|---|---|---|
| 混凝土贡献 | 钢筋贡献 | 总能力 | 混凝土贡献 | 钢筋贡献 | 总能力 | |
| 公规 | 334 | 2 767 | 3 101 | 334 | 2 476 | 2 810 |
| 城规 | 3 721 | 2 767 | 6 488 | 3 207 | 2 476 | 5 683 |
| 比值 | 11.14 | 1.00 | 2.09 | 9.60 | 1.00 | 2.02 |
抗压承载能力可以提高至原来的 2 倍,单桩的抗拉承载能力,可比非抗震设计时提高 25% ;在验算桩基础截面抗弯强度时,截面抗弯能力可采用材料强度标准值计算。
显然,在墩柱进入塑性工作后,按两本规范计算的桩基础的抗震需求与地震动输入无关,只取决于墩柱的截面抗弯强度,因此是一样的。而抗震能力方面,按《城规》计算的单桩抗压承载能力和抗拉承载能力分别是《公规》的 2 倍和 1.25 倍。表 4 则对按两本规范进行的单桩抗弯强度进行了比较,结果表明,按《城规》计算单桩抗弯能力约是《公规》的 1.50 倍,《公规》偏于保守。
表 4 单桩抗弯强度比较
| 计算项目 | 纵桥向 | 横桥向 | |
|---|---|---|---|
| 轴力/kN | -1611 | -2061 | |
| 抗弯强度kN·m | 城规 | 548 | 440 |
| 公规 | 375 | 275 | |
| 比值 | 1.46 | 1.60 |
2.5 固定支座的验算比较
固定支座按照能力保护构件设计,在 E2 地震下,验算支座的水平抗力。按照能力设计方法,支座的水平力需求与墩柱剪力需求相同,因此两规范对于固定支座的验算结果是相同的。
3 结语
针对本文中的连续梁桥,依据两本抗震规范,通过对地震动输入、桥墩和桩基础及支座的抗震需求与能力的定量比较和分析,得出如下结论。
(1)两本规范的地震动参数不尽相同,《城规》的设计加速度反应谱比《公规》的大,针对本桥梁,E1 地震下纵桥向与横桥向前者是后者的 1.2 倍和 1.1 倍,E2 地震下为 1.8 和 1.3 倍。
(2)两本规范反应谱的差异导致 E1 地震下墩柱弯矩需求的不同,而抗弯能力则相同;E2 地震下墩柱水平地震力和位移需求的差异,也主要来自反应谱,但纵桥向要考虑活动墩上滑动支座摩擦的影响;位移能力上,由于等效塑性铰长度不同,纵桥向《城规》是《公规》的 1.3 倍,横桥向都采用非线性静力分析,两者相同。
(3)对于墩柱塑性铰区域斜截面抗剪能力,《公规》忽略了轴压力的贡献,较为保守。《城规》中计算混凝土的贡献较《公规》大 10 倍,钢筋贡献两本规范计算结果一致,总的抗剪能力《城规》约为《公规》的 2 倍。
(4)单桩的抗弯能力,《城规》采用材料标准值,而《公规》采用材料设计值,计算结果前者是后者的 1.5 倍,《公规》偏于保守。
(5)固定墩支座水平抗力与墩柱剪力需求相同,与地震力无关,两本规范是相同的。
参考文献:
叶爱君, 管仲国. 桥梁抗震 [M]. 北京: 人民交通出版社. 2011.
JTG/T B02-01—2008 公路桥梁抗震设计细则 [S].
CJJ 166—2011 城市桥梁抗震设计规范 [S].
范立础, 王俊杰. 桥梁抗震设计规范的现状与发展趋势 [J]. 地震工程与工程振动, 2001, 21(2): 71-77.
薛瑞杰, 袁万城. 国内外桥梁延性抗震构造设计比较 [J]. 工程抗震与加固改造, 2009, 31(2): 1-8.
贡金鑫,张勤,王雪婷.从汶川地震中桥梁震害看现行国内外桥梁抗震设计方法(二)[J]. 公路交通科技,2010,27(10):35-46. ↩
贡金鑫,张勤,王雪婷.从汶川地震中桥梁震害看现行国内外桥梁抗震设计方法(一)[J]. 公路交通科技,2010,27(9):44-54. ↩