毛勇,陈方有²
(1. 南京市公共工程建设中心,江苏南京 210019;2. 同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:鉴于大跨度悬索桥抗震性能研究的复杂性和特殊性,以南京仙新路特大跨度悬索桥为例,阐述悬索桥抗震性能研究的全过程,并分析行波效应对该桥地震响应的影响。结果表明:该桥的第一阶振型周期超过 25.0\mathrm{~s~},在常规体系 E2 地震下,桥塔及其基础保持弹性,但中央扣受拉破坏,从而使主梁位移过大;采用将中央扣作为牺牲构件,同时在塔梁间设置液压粘滞阻尼器的纵向减震体系后,能显著减小塔上支座、梁端的纵向位移以及主引桥相对位移;同时,能小幅度减小塔底和承台底地震内力;行波效应对减震体系关键位置的地震内力和地震位移的影响较小。
关键词:特大跨度悬索桥;动力特性;抗震性能;行波效应;中央扣;牺牲构件
中图分类号:U442.5°5 文献标志码:B 文章编号:1009-7716(2020)02-0041-05
Study on Seismic Performance of Nanjing Xianxin Road Super Long-span Suspension Bridge
Abstract: The dynamic property and seismic response of long-span suspension bridge are all very complicated, and the dynamic property and seismic environment of each suspension bridge are all different. Therefore, it is necessary to study the seismic performance in detail. Taking a super long-span suspension bridge with the main span 1 760 m in Xianxin Road of Nanjing as an example, this paper sets forth the whole process of the study on the seismic performance of suspension bridge and analyzes the impacts of traveling wave effect on the seismic response of this bridge. The results show that the first mode period of this bridge is beyond 25.0 s and belongs to the long period. In a conventional E2 earthquake, the bridge pylon and its foundations remain elastic, but the seismic axial force of the central buckle is too high and causes the tensile failure so as to make the main beam displacement too large. After adopting the central buckle as sacrificial component and also setting up the longitudinal damping system of hydraulic viscous damper between the pylon and beam, the longitudinal displacements of the pylon support and beam end, and the relative displacement of the main approach bridge can be obviously decreased, and meanwhile the earthquake-induced internal forces at the bottoms of the pylon and base slab can be reduced slightly. The traveling wave effect has little influence on the seismic internal force and seismic displacement at the key position of the damping system.
Keywords: super-large-span suspension bridge, dynamic characteristics, seismic performance, traveling wave effect, central buckle, sacrificial component.
0引言
在我国近十几年的大地震灾害中,桥梁工程往往都会遭到严重破坏,不仅造成了巨大的经济损失,还导致通往灾区的交通生命线被切断,增加了救灾工作的难度1。 《中华人民共和国防震减灾法》规定:“建设工程必须按照抗震设防要求和抗震设计规范进行抗震设计,并按照抗震设计进行施工。”但是,我国现行的《城市桥梁抗震设计规范》和《公路桥梁抗震设计细则》只适用于跨度 150~\mathrm{m} 以下的梁桥和拱桥,对于悬索桥则要求进行专门的抗震研究。
邓育林以泰州长江公路大桥为例,对该桥进行了线性地震反应分析,探讨了大跨度三塔悬索桥地震反应的特点;袁万城等以广东汕头海湾大桥为例,对地震反应谱分析和地震时程分析的结果进行比较,指出了对大跨悬索桥采用时程分析的必要性;闫聚考等以一座三塔两跨悬索桥为例,分析了不同视波速下行波效应对大跨多塔悬索桥的影响,得出行波效应可能会增大塔梁相对位移和主引桥梁相对位移。
尽管针对悬索桥的抗震研究文献已有很多,但大跨度悬索桥的动力特性和地震反应非常复杂,而且每一座大跨度悬索桥的动力特性和所处的地震环境又各不相同。因此,在每一座大跨度悬索桥的建设中,桥梁的抗震安全性都是一个重要课题,必须进行详细的研究。本文以南京仙新路特大跨度悬索桥为例,阐述悬索桥抗震性能研究的全过程,并分析行波效应对该桥减震体系地震响应的影响。
1抗震设防标准确定
根据《城市桥梁抗震设计规范》对甲类桥的抗震设防要求,制定南京仙新路跨江大桥的抗震设防标准(见表 1)。其中,在 E2 地震作用下要求桥梁主塔、基础保持弹性,其余构件无损坏;因此,在 E1 地震作用下无需验算。
表 1 主桥抗震设防标准
| 地震重现期 | 结构性能要求 | 结构验算目标 |
|---|---|---|
| 475年 | 结构处于弹性工作状态,震后不需修理即可正常通车 | 无需验算 |
| 2500年 | 主塔基本弹性,支座等连接构件正常工作,基础基本弹性,其它构件无损坏 | 验算主塔抗弯强度,验算各基础竖向承载能力及抗弯强度,验算支座的强度或位移 |
2动力计算模型的建立
仙新路大桥为地锚式双塔单跨悬索桥,跨径布置采用 580\mathrm{m} + 1760\mathrm{m} + 580\mathrm{m} = 2920\mathrm{m},如图 1 所示。

图 1 主桥立面(单位:m)
主梁采用封闭式流线型扁平钢箱梁,总宽 31.5\mathrm{m},梁高 4\mathrm{m};主塔采用门式框架混凝土结构,塔高 263.8\mathrm{m};主塔基础采用群桩基础,为钻孔摩擦桩,承台下设 66 根桩,桩径为 2.8\mathrm{m};主桥支座采用纵向滑动、横向约束的球形钢支座(常规体系);主跨跨中设置柔性中央扣,每个中央扣含两根拉索,每根拉索含 211 丝 \mathrm{b}5 超强钢丝。
根据悬索桥设计图纸,采用 SAP2000 软件建立三维桥梁结构动力计算模型(如图 2 所示),建模时考虑了相邻一联引桥的影响。主梁、主塔、塔座和承台采用梁单元模拟,主缆和吊杆采用桁架单元模拟。其中,主梁节点通过主从约束与吊杆连接;主缆和主塔考虑了恒载几何刚度的影响5,6。各群桩基础采用六弹簧模型模拟。
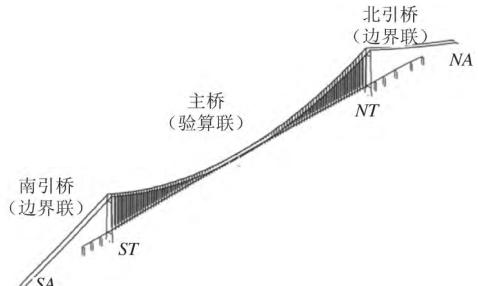
图 2 动力计算模型
在非线性时程反应分析中,采用理想弹塑性恢复力模型考虑滑动支座的摩擦耗能作用,滑动摩擦系数取 2\%,支座滑动临界位移取 2\mathrm{mm}7。
柔性中央扣在非线性时程分析时采用只受拉的桁架单元模拟,但在动力特性分析和反应谱分析时采用普通桁架单元模拟。
3动力特性分析
基于所建立的桥梁动力计算模型,对该桥进行动力特性分析。从主桥 6 阶典型振型及其周期(见表 2)中可见主桥的一阶振型为主梁对称侧弯振型,周期长达 25.03\mathrm{~s~},属于长周期;而主梁纵飘振型为第 15 阶,周期为 4.59\mathrm{~s~}。
表 2 主移动力特性
| 阶数 | 周期/s | 振型描述 |
|---|---|---|
| 1 | 25.03 | 主梁一阶正对称侧弯 |
| 2 | 12.90 | 主梁一阶反对称竖弯 |
| 5 | 7.52 | 主塔侧弯 |
| 10 | 5.47 | 主跨主缆侧弯 |
| 15 | 4.59 | 主梁纵飘+边主缆竖弯 |
| 16 | 4.45 | 边跨主缆侧弯 |
4地震动输入选择
主桥的地震动参数由江苏省地震工程研究院提供。地震反应分析选用地震重现期分别为 475a 和 2500\mathrm{a} 的地震动参数作为地震动输入,包括地震加速度反应谱和地震加速度时程(每组 7 条)。进行地震反应分析时,还考虑了竖向地震动的影响,竖向地震动为水平向地震动的 2/3;进行地震加速度非线性时程分析时,取 7 条地震加速度时程的计算结果的平均值。
此外,本文还考虑了行波效应的影响,视波速采用江苏省地震工程研究院提供的建议值 3400\mathrm{m / s}。2500a 重现期的 7 条地震加速度时程与对应反应谱的拟合情况以及其中一条地震加速度时程曲线如图 3 所示。
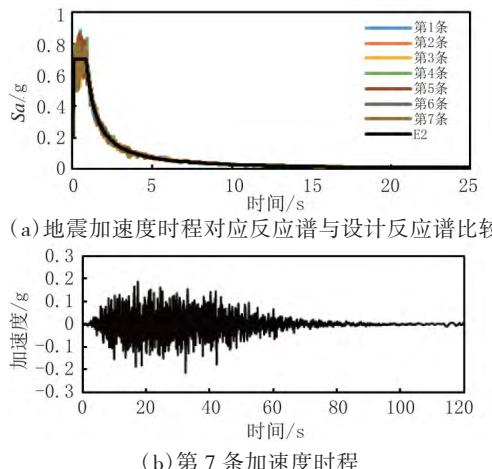
图 3 地震动输入(重现期 2500 年)
5常规体系桥梁抗震性能分析
5.1地震反应谱分析
在全桥结构动力特性分析的基础上进行地震反应谱分析,地震动输入方式分别为纵桥向 ^+ 竖向和横桥向 ^+ 竖向,计算前 1600 阶振型的贡献,振型组合方法采用 CQC 法,方向组合方法采用 SRSS 法,结构的振型阻尼比为 0.02。
为确定桥梁的控制设计截面,本节给出了 E2 地震沿纵向 ^+ 竖向、横向 ^+ 竖向输入下的桥塔轴力、剪力、弯矩以及位移包络图(如图 4 所示),可以看出:
(1) 在纵向 ^+ 竖向输入时,轴力、剪力和弯矩最大值均出现在塔底截面,且在中塔柱 1/3 处截面存在较大弯矩,此外在下横梁与塔柱交界处剪力存在突变,因此中塔柱 1/3 处截面、下横梁下侧塔柱截面和塔柱底截面为最不利截面;位移最大值出现在中塔柱 1/3 处截面。
(2)在横向 ^+ 竖向输入时,桥塔在横向的弯矩反应符合框架结构的特点,最不利截面为上横梁下侧塔柱截面、下横梁上、下侧塔柱截面、横梁端部截面和塔柱底截面;位移最大值出现在塔顶。
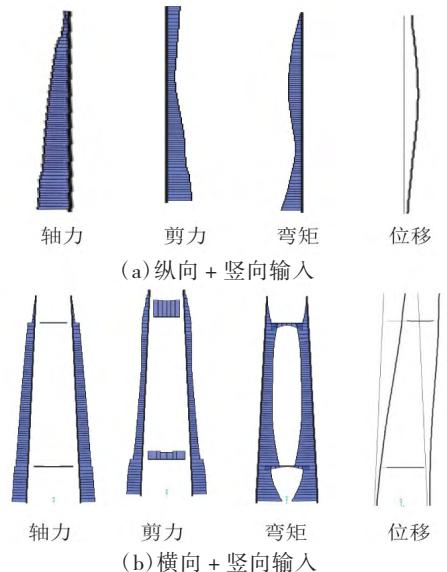
图 4 主塔地震内力、位移包络图
在复杂桥梁的地震反应分析中,由于反应谱方法存在振型组合问题且不能考虑各种复杂的非线性因素,因此计算结果仅用于对后续时程分析结果的校核,且两者对比结果基本在 20\% 以内。
5.2地震反应时程分析
由于主桥结构基本保持对称,以下分析仅列出主桥南侧(地震反应较大的一侧 ) 结构的结果。E2 地震作用下主桥南侧主塔控制截面的抗弯需求及验算结果见表 3。从表 3 中可以看出:在 E2 地震作用下,主塔均保持弹性状态,且能力需求比均在 3.12 以上,抗弯能力较富余。
表 3 南侧主塔抗弯能力验算 kN·m
| 输入 | 位置 | 抗弯需求 | 抗弯能力 | 能力/需求 |
|---|---|---|---|---|
| 纵向+竖向 | 中塔柱1/3处 | 1.09E+06 | 3.48E+06 | 3.18 |
| 下横梁下侧塔柱 | 9.52E+05 | 5.22E+06 | 5.48 | |
| 塔底 | 1.89E+06 | 6.47E+06 | 3.43 | |
| 横向+竖向 | 上横梁下侧塔柱 | 5.82E+05 | 1.92E+06 | 3.31 |
| 下横梁上侧塔柱 | 1.05E+06 | 4.27E+06 | 3.12 | |
| 下横梁下侧塔柱 | 6.52E+05 | 3.36E+06 | 5.15 | |
| 上横梁端部 | 5.58E+05 | 4.73E+06 | 8.48 | |
| 下横梁端部 | 3.67E+05 | 2.44E+06 | 6.65 | |
| 塔底 | 1.23E+06 | 4.29E+06 | 3.49 |
E2 地震作用下主塔基础最不利单桩截面的抗弯需求及验算结果见表 4。可以看出:在 E2 地震作用下,基础最不利单桩抗弯能力需求比均在 3.59 以上,抗弯能力较富余。其中,桩身钢筋按 0.84\% 纵筋配筋率和 0.60\% 体积配箍率考虑。
表 4 主塔基础最不利单桩抗弯能力验算 kN·m
| 输入 | 位置 | 抗弯需求 | 抗弯能力 | 能力/需求 |
|---|---|---|---|---|
| 纵向+竖向 | ST | 1.06E+04 | 3.81E+04 | 3.59 |
| NT | 9.41E+03 | 3.93E+04 | 4.17 | |
| 横向+竖向 | ST | 1.06E+04 | 3.96E+04 | 3.74 |
| NT | 9.03E+03 | 3.98E+04 | 4.41 |
在 E1 和 E2 纵向 ^+ 竖向地震作用时,中央扣会产生较大的地震轴拉力,其地震轴拉力分别为 8.95\mathrm{E} + 03\mathrm{kN} 和 2.05\mathrm{E} + 04\mathrm{kN},均超过其屈服强度 7.32\mathrm{E} + 03\mathrm{kN},发生受拉破坏。
由于柔性中央扣失效后,主梁的纵向地震位移会显著增大,但对主塔及其基础的地震反应影响较小。因此,在 E2 纵向 ^+ 竖向地震作用时,有无中央扣的塔梁间支座纵向地震位移和主引桥相对位移(见表 5) 中可以看出:中央扣失效后,支座纵向位移和主引桥相对位移分别增加了 35\% 和 24\%。
表 5 支座位移、主引桥相对位移 m
| 位置 | 有中央扣 | 无中央扣 | (无-有)/有 |
|---|---|---|---|
| 支座 | 0.51 | 0.69 | 35% |
| 主引桥 | 0.58 | 0.72 | 24% |
综上所述,在 E2 地震作用下,主桥桥塔和基础保持弹性状态,存在的主要问题包括:中央扣地震轴力太大,设计无法满足要求;而中央扣失效后会使主梁纵向位移显著增大,导致纵向滑动支座地震位移以及主引桥相对位移超出设计允许值。为此,抗震设计中将柔性中央扣作为牺牲构件,在给定拉力下失效,同时在塔梁间设置纵向液压粘滞阻尼器,以减小主梁的地震位移8。
6 减震体系抗震性能分析
仙新路特大悬索桥采用的纵向减震体系将柔性中央扣作为牺牲构件,拉力超过 3000\mathrm{kN} 后失效,同时在塔梁间设置纵向液压粘滞阻尼器(每个塔梁连接处各布置 2 个),以减小主梁的地震位移。粘滞阻尼器的速度指数根据静力性能要求确定,取 0.1,而阻尼系数经过优化分析后,兼顾主梁位移、主引桥相对位移以及主塔地震内力,取 2500,力的单位为 \mathrm{kN},速度的单位为 \mathrm{m / s}。
本节针对这一减震体系,采用 E2 地震输入,进行减震效果分析,然后分析行波效应对减震体系地震反应的影响。
6.1 减震体系减震效果分析
E2 纵向 ^+ 竖向地震作用下减震体系和常规体系的桥塔关键截面内力以及主塔承台底对比见表 6。从表 6 中可以看出:采用减震体系后,桥塔和承台底轴力、剪力和弯矩都有所减小,其中轴力减幅较小,在 5\% 以内;弯矩减幅较大,为 8\% \sim 16\%。
表 6 减震体系对主塔地震内力的减震率
| 位置 | 轴力 | 剪力 | 弯矩 |
|---|---|---|---|
| ST中塔柱1/3处 | -3% | -6% | -15% |
| ST下横梁下侧塔柱 | -2% | -7% | -16% |
| ST塔底 | -2% | -8% | -10% |
| NT中塔柱1/3处 | -4% | -6% | -13% |
| NT下横梁下侧塔柱 | -1% | -4% | -13% |
| NT塔底 | -1% | -6% | -8% |
| ST承台底 | -1% | -8% | -11% |
| NT承台底 | 0% | -8% | -9% |
E2 纵向 ^+ 竖向地震作用下,常规体系和减震体系关键位置的纵向位移见表 7,从表 7 中可以看出:相比于常规体系,减震体系的主梁纵向位移平均减小约 56\%,主引桥相对位移减幅约为 46\%,主塔的位移减幅较小。E2 纵向 ^+ 竖向第一条时程波输入下,常规体系与减震体系主桥南侧的主、引桥梁端的位移时程如图 5 所示,可以看出阻尼器限制了主桥位移,从而使主引桥相对位移显著降低。
表 7 减震体系对关键位置位移的减震效果
| 位置 | 常规体系 | 减震体系 | (减震-常规)/常规 |
|---|---|---|---|
| 塔顶 | 0.18 | 0.16 | -11% |
| 中塔柱1/3处 | 0.42 | 0.36 | -14% |
| 梁端 | 0.60 | 0.26 | -57% |
| 跨中 | 0.59 | 0.26 | -56% |
| 主引桥 | 0.72 | 0.39 | -46% |
在 E2 纵向 ^+ 竖向地震作用下,常规体系中主桥支座位移最大值为 0.69\mathrm{m},在减震体系中显著减小为 0.32\mathrm{m},减小了 54\%。
6.2 行波效应对减震体系地震反应的影响
在 E2 纵向 ^+ 竖向地震作用下,是否考虑行波效应的减震体系主塔承台底及桥塔关键截面内力。
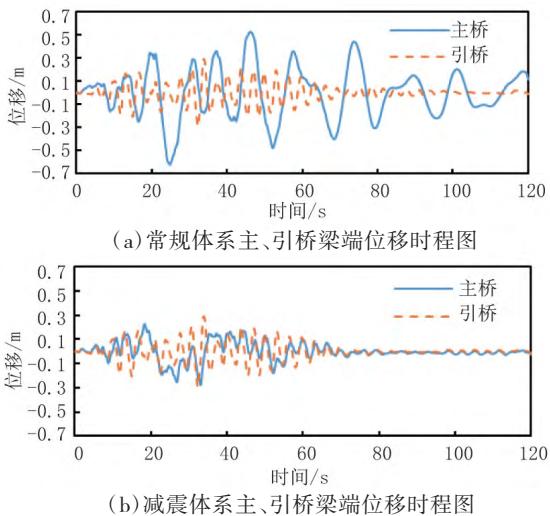
图 5 主、引桥梁端位移时程图
对比见表 8。从表 8 中可以看出:桥塔和承台底轴力变化较小,总体在 10\% 以内;南桥塔及南承台底的弯矩明显降低,减小了 10\% \sim 19\%,北桥塔及北承台底的弯矩变化很小,在 5\% 以内。
表 8 行波效应对地震内力的影响率
| 位置 | 轴力 | 剪力 | 弯矩 |
|---|---|---|---|
| ST中塔柱1/3处 | -10% | 37% | -19% |
| ST下横梁下侧塔柱 | -7% | -6% | -14% |
| ST塔底 | -7% | -11% | -10% |
| NT中塔柱1/3处 | 6% | 28% | -2% |
| NT下横梁下侧塔柱 | 8% | 4% | 3% |
| NT塔底 | 7% | 1% | 3% |
| ST承台底 | -5% | 0% | -13% |
| NT承台底 | 8% | 9% | 2% |
E2 纵向 ^+ 竖向地震作用下,考虑行波效应后减震体系关键位置的纵向位移,并与未考虑行波效应的减震体系作对比见表 9,从表 9 中可以看出:考虑行波效应增大了塔顶位移,增长了 19\%,对其余关键位置的地震位移影响不大。
表 9 行波效应对减震体系纵向位移的影响 m
| 位置 | 未考虑行波效应 | 考虑行波效应 | (考虑-未考虑)/未考虑 |
|---|---|---|---|
| 塔顶 | 0.16 | 0.19 | 19% |
| 中塔柱1/3处 | 0.36 | 0.33 | -8% |
| 梁端 | 0.26 | 0.28 | 8% |
| 跨中 | 0.26 | 0.25 | -4% |
| 主引桥 | 0.39 | 0.39 | 0% |
在 E2 纵向 ^+ 竖向地震作用下,考虑行波效应后减震体系纵向活动支座的纵向位移,并与未考虑行波效应的减震体系作对比(见表 10)。可以看出,行波效应对减震体系支座位移影响很小。
表 10 行波效应对减震体系支座位移的影响 m
| 位置 | 未考虑行波效应 | 考虑行波效应 | (考虑-未考虑)/未考虑 |
|---|---|---|---|
| ST | 0.32 | 0.30 | 6% |
| NT | 0.29 | 0.30 | 3% |
7结论
基于上述研究,本文主要得出如下结论:
(1) 主桥的一阶振型为主梁对称侧弯振型,周期长达 25.03\mathrm{~s~},属于长周期。
(2)在常规体系 E2 地震下,桥塔及其基础保持弹性,但中央扣地震轴力过大,会发生受拉破坏,从而使主梁位移过大。
(3)主桥采用的纵向减震体系为:将柔性中央扣作为牺牲构件,在给定拉力下失效,同时在塔梁间设置纵向液压粘滞阻尼器。该减震体系能显著减小塔上支座、梁端的纵向位移以及主引桥之间的纵向相对位移,减幅为 50\% 左右;同时,能小幅度减小塔底和承台底地震内力。
(4)行波效应对减震体系关键地震内力和地震位移的影响较小。
参考文献:
叶爱君. 桥梁抗震 [M]. 北京:人民交通出版社,2008:1-143. ↩
邓育林,彭天波,李建中,等. 大跨度三塔悬索桥动力特性及抗震性能研究 [J]. 振动与冲击,2008,27(9):105-110.
袁万城,胡世德,范立础. 悬索桥抗震分析方法 [C]. 北京:中国土木工程学会桥梁及结构工程学会第 11 届年会论文集,1994.
闫聚考,李建中,彭天波. 行波效应对大跨多塔悬索桥纵向约束体系影响研究 [J]. 结构工程师,2014(4):46-51.
叶爱君,周连绪,陈光,等. 大跨度斜拉桥倒 Y 形混凝土桥塔的横向拟静力试验 [J]. 土木工程学报,2018(9):66-74. ↩
周连绪,叶爱君. 千米级斜拉桥横向减震体系振动台试验 [J]. 中国公路学报,2019,32(9):71-79. ↩
Zhou L, Wang X, Ye A. Shake table test on transverse steel damper seismic system for long span cable-stayed bridges [J]. Engineering Structures,2019,179:106-119. ↩
叶爱君,胡世德,范立础. 超大跨度斜拉桥的地震位移控制 [J]. 土木工程学报,2004(12):40-45. ↩