杨当 ^{1} ，王靖程 ^{1,2} ，叶爱君 ^{1,3} (1. 同济大学土木工程防灾国家重点实验室，上海市 200092；2. 同济大学桥梁工程系，上海市 200092)

摘要：在桩基桥梁的地震反应分析中，桩 - 土动力相互作用是个重要的问题，而对于采用低桩承台基础的桥梁，承台埋在土面以下，还存在土与承台之间的动力相互作用。目前，地震反应分析中一般不考虑土 - 承台动力相互作用的影响，相关研究也很少。为此，利用 OpenSees 有限元分析程序，基于p - y曲线建立了土 - 结构一体化桩基单墩模型，选择 40 条实际岩石场地地震记录作为输入，开展了考虑土 - 承台动力相互作用的桩基桥梁地震反应分析。结果表明，考虑土 - 承台动力相互作用后，结构的基本周期会减小，墩底曲率会明显增大，桩顶曲率会大幅减小，但墩顶位移的减小可以忽略。

关键词：桥梁；群桩基础；地震反应；土 - 结构一体化模型；土 - 承台动力相互作用

中图分类号：U442.5°5 文献标志码：A 文章编号：1009-7716(2024)01-0199-06

Influence of Soil- Base Slab Dynamic Interaction on Seismic Response of Pile Foundation Bridges in Sandy Soil Site

YANG Dang, WANG Jingcheng, YE Aijun (199)

Abstract: Soil- pile dynamic interaction is an important issue in the seismic response analysis of pile foundation bridges. For a bridge with the low- pile base slab foundation, the base slab is buried below the earth surface, and there is also dynamic interaction between soil and base slab. At present, the influence of soil- base slab dynamic interaction is generally not considered in seismic response analysis, and is rarely studied in the literature. Therefore, based on the p- y curve method, a soil- structure integrated pile foundation single- pier model is established by using OpenSees finite element analytical procedure. 40 actual rock site seismograms are selected as input to carry out the seismic response analysis of pile- supported bridge considering the soil- base slab dynamic interaction. The results show that the basic period of structure will decrease after considering the soil- base slab dynamic interaction, and the curvature of pier- bottom section will obviously increase and the curvature of pile- head section will greatly decrease, but decrease of displacement at the pier top can be neglected.

Keywords: bridge; foundation of group pile; seismic response; soil- structure integrated model; soil- base slab dynamic interaction

PDF BibTeX

0 引言

大量桩基桥梁的抗震设计实践表明，桩基础往往由抗震需求控制设计。实际工程中，由于桥位地形场地条件、施工难度、美观与整体协调等多因素的影响，桩基承台埋置深度各有不同。根据承台的埋置深度不同，群桩基础可分为两类：承台底面在土面以上为高桩承台基础，反之则为低桩承台基础。对于低桩承台基础，地震作用下，不仅存在桩 - 土动力相互作用，还存在土 - 承台动力相互作用。但在工程实践中，通常不考虑土 - 承台动力相互作用，忽略承台侧土抗力对于桩基水平承载力的贡献。这种设计方法虽然比较容易操作，但是否会导致桩基础的抗震设计过于保守，以至于显著增大抗震投入，有必要进行仔细研究。

目前，土 - 承台水平向相互作用研究主要集中在静力方面。Hararika 等建立了考虑承台作用的15\mathrm{m}单桩有限元模型，研究得出承台对群桩基础水平承载力的贡献占总承载力的40\%左右，且承台水平承载力随承台埋深和桩长的增大而增大。Mohamed Ashour 等利用应变模模型分析法研究桥梁群桩基础在水平荷载下与承台的相互作用，发现承台承担的水平荷载占整个群桩基础总承担的水平荷载的比例受桩与承台的连接方式与砂土的密实度影响，最大可达53\%。对于土 - 承台动力相互作用的研究还很少，仅有张永亮等以某一实际工程为背景，采用线弹性\mathrm{m}法分析了承台侧向土刚度对曲线匝道桥抗震性能的影响。

总体而言，现有研究没有阐明土 - 承台动力相互作用对桩基桥梁地震反应的影响。为解决这一问题，本文以一砂土场地常规梁桥为工程背景，参考土 - 扩大基础动力相互作用的模拟方法，提出了土 - 承台动力相互作用的简化分析方法，利用 OpenSees 程序建立了考虑土 - 承台动力相互作用的场地 - 桩基础 - 单墩一体化模型，并从太平洋地震研究中心数据库 (Pacific Earthquake Engineering Research Center) 选取 40 条岩石场地地震记录作为地震输入，进行地震反应分析，细致分析土 - 承台动力相互作用对桩基桥梁地震反应的影响。

1 考虑土-承台动力相互作用的桩基桥梁单墩有限元模型

本文以砂土场地典型常规梁桥的桥墩及基础为对象开展研究。桥墩高6.5\mathrm{m}，采用钢筋混凝土圆形截面，直径2\mathrm{m}。上部结构重量按桥墩受压承载力的10\%取值，即墩的轴压比为 0.1。承台尺寸为8\mathrm{m}\times 5\mathrm{m}\times 3\mathrm{m}，平面布置为3\times 2混凝土灌注桩，桩长30\mathrm{m}，桩径1\textrm{m}，桩间距3\textrm{m}。墩和桩基础均采用 C40 混凝土材料。砂土场地，上层8\textrm{m}为松砂，下层22\textrm{m}为密砂。

1.1 土-承台动力相互作用的简化模拟

扩大基础在形状、尺寸、构造、埋置深度和与上部结构的连接方式等方面都与桩基承台类似，因此，本文借鉴土 - 扩大基础的动力相互作用模拟方法⁴来建立土 - 承台动力相互作用模型，如图 1 所示。

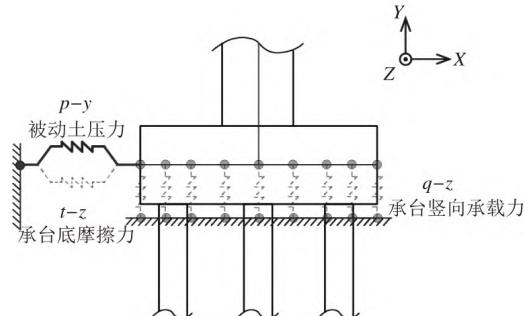
土-承台动力相互作用模拟示意图
图 1 土 - 承台动力相互作用模拟示意图

文献⁴中，土与扩大基础之间的相互作用力主要有基础侧面的被动土压力、基础底面的滑动摩擦力和基础底面的土压力。其中，基础底面的滑动摩擦力又取决于土压力。但在群桩基础的受力分析中，由于桩身竖向刚度远大于承台底面的土体竖向刚度，所以一般忽略土体承载力⁵。针对前述桥梁基础和场地条件，本文采用\mathrm{ATC - 40}⁶计算了承台底面土体总竖向刚度，为4.22\times 10^{5}\mathrm{kN / m}。同时按照《公路桥涵地基与基础设计规范》⁵计算了群桩竖向刚度，为9.28\times 10^{6}\mathrm{kN / m}，前者为后者的4.5\%。因此，本文在考虑土 - 承台动力相互作用时，忽略承台底面的水平摩阻力和承台竖向承载力的贡献，仅考虑水平向的被动土压力，在承台侧设置非线性温克勒弹簧，即水平向p - y弹簧，如图 1 所示。

承台侧p - y弹簧的极限承载力由库伦被动土压力公式⁷计算，假设其随深度线性变化，按三角形分布，计算公式如下：

p_{\mathrm{ult}} = 0.5\gamma K_{\mathrm{p}}D_{f} \tag{1}

式中：\gamma为土的有效重度，\mathrm{kN / m^3}；D_f为承台底面标高，\mathrm{m}；K_{\mathrm{p}}为被动土压力系数，可按式 (2) 计算：

K_{\mathrm{p}} = \frac{\cos^{2}(\phi + \alpha)}{\cos^{2}\alpha\cdot\cos(\alpha - \delta)\left[1 - \sqrt{\frac{\sin(\phi + \delta)}{\cos(\alpha - \delta)}\cdot\cos(\alpha + \beta)}\right]} \tag{2}

式中：\phi为土的摩擦角；\alpha为承台的倾斜角；\beta为承台侧填土面的倾角；\delta为土对承台的摩擦角。

1.2 土-结构一体化模型

本文采用如图 2 所示的土 - 结构一体化模型，来研究土 - 承台动力相互作用对结构地震反应的影响。在数值模型中考虑土面标高在承台顶面和在承台底面两种情况。为了方便称呼，在后文中分别简称为承台有侧土和承台无侧土。该模型主要包括三个部分，一是包括上部结构、墩、承台和桩的桥梁结构部分，二是由松砂和密砂构成的土体部分，三是土与桩和承台的土弹簧部分。

1.2.1 结构模拟

结构模型中，上部结构采用集中质量节点模拟，与墩顶节点采用主从约束。墩柱和桩身均采用基于位移的梁柱单元来模拟弹塑性性能，单元长度为0.5\mathrm{m}，一个单元设置 5 个积分点。墩柱和桩身的钢筋混凝土截面的纤维划分如图 2 所示。承台作为集中质量节点参与运算，从上到下共设置 3 个节点，300~\mathrm{t}质量全部赋予承台中心节点。墩柱和桩身保护层混凝土抗压强度为34~\mathrm{MPa}，屈服应变和极限应变分别为 0.002 和 0.005，核心混凝土采用 Mander 模型⁸，对应 OpenSees 材料库中的 Concrete04 材料模型。钢筋采用 HRB400 钢筋，弹性模量为200\mathrm{GPa}，硬化率为 0.01，对应 OpenSees 材料库中 Steel02 材料模型。

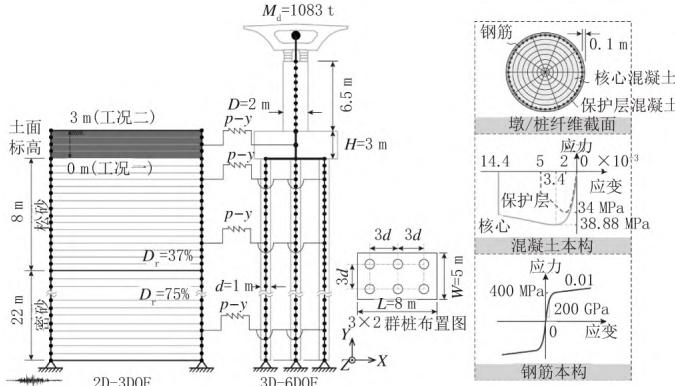
土-结构一体化模型示意图
图 2 土 - 结构一体化模型示意图

1.2.2 土体模拟

土体分为上层的松砂和下层的密砂，在 OpenSees 中采用 quad 二维单元模拟，单元尺寸为长50~\mathrm{m}\times高0.5\mathrm{m}。单元材料采用 OpenSees 材料库中的 PressureDependMultiYield（PDMY）材料模型。本文参考 Wang 等的研究成果⁹确定 PDMY 材料各参数的取值，详见表 1。

1.2.3 桩土相互作用

本模型以水平方向\mathcal{X}作为地震动输入方向，考虑到与\mathcal{X}垂直的水平方向\mathcal{Z}地震反应很小，因此选择将土体和结构的\mathcal{E}方向平动自由度约束。同时，因为竖直方向y无加速度输入，本模型主要关注结构和土体水平向地震反应，所以选择将桩尖竖向平动自由度

表 1 土体模型材料本构参数取值

材料特性	上层松砂	下层密砂
土密度ρ/(t·m-3)	1.946	2.033
密实度D1/%	37.0	75.0
参考剪切模量G1/kPa	56 731	108 304
体积模量B1/kPa	151 283	288 811
内摩擦角Φ/(°)	32.0	38.7
峰值剪应变gmax	0.1	0.1
参考约束压力Pz	80	10
压力指数d	0.1	0.5
相位角Φrr/(°)	22.2	29.3
体积收缩率cont	0.07	0.07
体积膨胀系数dilat1	0.3	0.6
体积膨胀系数dilat2	2	3
孔隙率e	0.74	0.60

约束，认为桩尖固定在基岩中。桩身与土体的相互作用模拟，即砂土p - y曲线本构模型模拟，以下做详细介绍。

对于砂土p - y曲线的参数取值，可以参考 API 颁布的规范。该规范参考了 O'Neil 和 Murchison 于 1983 年的研究¹⁰。该研究将砂土的p - y关系曲线以双曲正切函数形式表示，我国《港口工程桩基规范》也参考了此方法来计算桩基础的水平作用，具体公式如式（3）所示。

浅层砂土水平方向的极限承载力p_{\mathrm{us}}和深层砂土水平方向的极限承载力p_{\mathrm{ud}}由式（3）定义。以下两式计算得到的较小值作为砂土中桩基单位长度的水平极限承载力p_{\mathrm{u}}(\mathrm{kN} / \mathrm{m})

\begin{array}{l}p_{\mathrm{us}} = (C_1\times H + C_2\times D)\times \gamma \times H \\ p_{\mathrm{ud}} = C_3\times D\times \gamma \times H \end{array} \tag{3}

式中：H为土体深度，\mathrm{m}；D为桩径，\mathrm{m}；\gamma为砂土有效重度，\mathrm{kN} / \mathrm{m}^3；C_1, C_2, C_3为 API 规范中由图查得的系数，该系数与土体内摩擦角有关。

砂土的p - y曲线关系由式（4）定义，

p = A\times p_{\mathrm{u}} \times \tanh \left[\frac{n_{\mathrm{h}}\times H}{A\times p_{\mathrm{u}}} y \right] \tag{4}

式中：n_{\mathrm{h}}为地基初始刚度，与砂土相对密实度D_{\mathrm{r}}和内摩擦角\theta有关，可通过 API 规范中的图查得；A为荷载系数，对于静载，由式（5）计算，对于循环荷载，A可取为 0.9。

A = \left(3.0 - 0.8\frac{H}{D}\right)\geqslant 0.9 \tag{5}

在 OpenSees 材料库中，砂土的p - y关系采用 PySimple1 材料模拟，需要输入的参数为水平极限承载力p_{\mathrm{u}}和土体反力等于50\%极限承载力时对应的桩身位移y_{50}，通过反解p - y曲线关系式可得到y_{50}定义式：

y_{50} = \frac{A}{n_{\mathrm{h}}}\frac{p_{\mathrm{u}}}{\kappa H}\operatorname {artanh}\left(\frac{0.5}{A}\right) \tag{6}

2 地震动输入选择

本文采用场地 - 桩基 - 单墩一体化模型进行地震反应分析，应选择基岩地震动进行地震反应分析。为此，从太平洋地震研究中心（PEER）NGA 地震动数据库中选择了 40 条岩石场地地震记录作为地震输入，具体选波的方式参考了 Baker 等的研究¹¹。因为本模型仅考虑水平地震动下的结构反应，因此每条地震记录只选择了其中一个水平分量作为输入，40 条地震波的反应谱如图3(\mathrm{a})所示，图3(\mathrm{b})、3(\mathrm{c})代表性地给出了其中两条地震记录的加速度时程曲线。

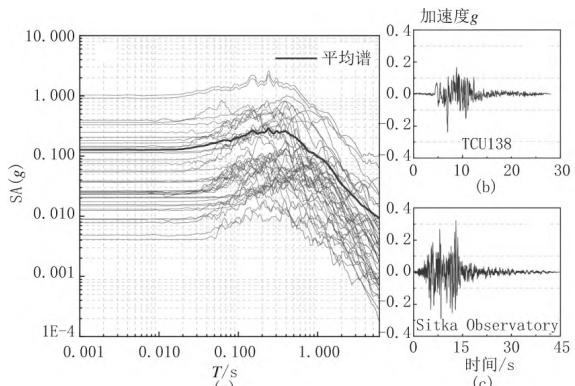
图 3 地震动输入

（a）所选地震动加速度反应谱；（b）、（c）其中的两条地震记录的加速度时程曲线

3 土-承台动力相互作用对桥梁地震反应的影响

本文首先对土 - 结构一体化模型进行了动力特性分析，无侧土时的基本周期为0.672\mathrm{~s}，有侧土时基本周期为0.580\mathrm{~s}，相对无侧土时减小了13.69\%。

3.1 有/无承台侧土时桥梁时程反应比较

本文首先采用 TCU138 波 [ 图3(\mathrm{b})] 作为地震输入，对两种情况下的场地和桥梁地震反应进行全面的比较。

图 4 给出了无承台侧土和有承台侧土两种情况下的土面加速度和承台水平加速度时程曲线，图中标记表示加速度的绝对值最大值。从图4(\mathrm{a})中可以得出，有承台侧土使土面加速度减小了1.6\%。从图4(\mathrm{b})中可以得出，有承台侧土使承台加速度减小了5.3\%。

图 5 给出了承台侧\mathrm{p - y}弹簧的反力时程曲线。

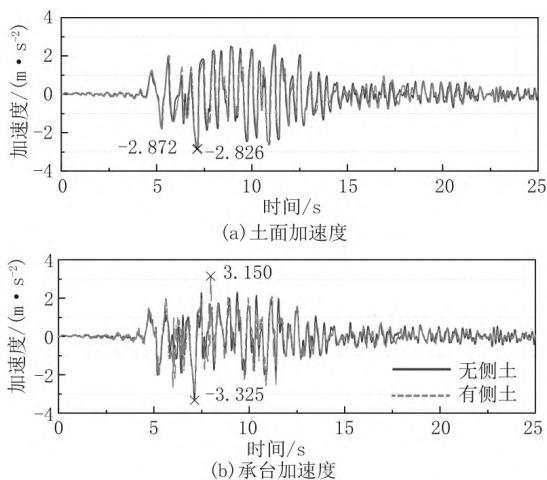
图 4 土面与承台加速度时程曲线

由图 5 可见，\mathrm{p - y}弹簧的反力达到了最大承载力。该反力大小约为承台水平惯性力最大值的 1.14 倍。

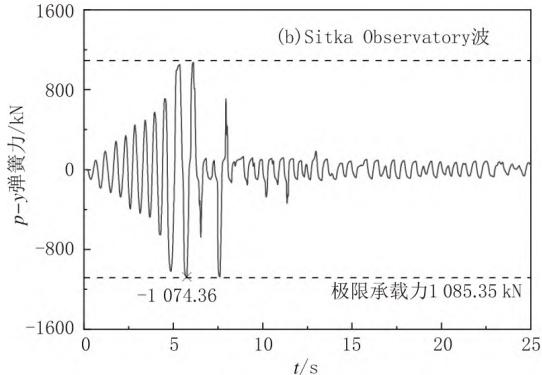
承台侧 p - y 弹簧反力时程曲线
图 5 承台侧p - y弹簧反力时程曲线

图 6 给出了有 / 无承台侧土两种工况下的结构水平地震位移包络图和时程曲线。由图 6 可见，土 - 承台动力相互作用使墩顶位移减小37.35\%，墩底位移减小18.54\%，桩顶位移减小15.60\%。

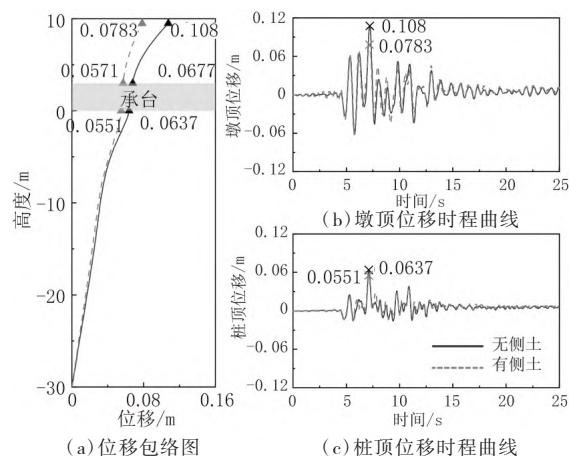
图 6 位移结果分析

图 7 给出了有 / 无承台侧土两种工况下的结构曲率包络图和时程曲线。由图 7 可见，土 - 承台动力相互作用显著减小了桩顶曲率包络值，减小幅度为45.19\%，但使墩底曲率增大了16.17\%，因为基本周期减小了。

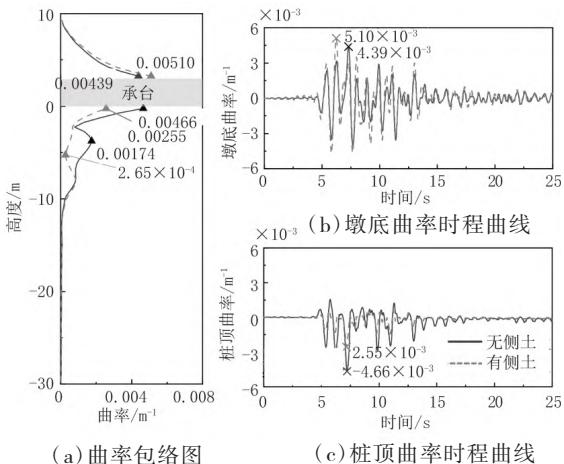
图 7 曲率结果分析

3.2 土-承台动力相互作用对桥梁地震反应的影响分析

为了考虑地震动特性对结构地震反应的影响，本文采用图 3 所示的 40 条实际地震记录作为地震输入。基于土 - 结构一体化模型分别进行了时程反应分析，并对关键反应最大值进行了统计分析。

图8(\mathrm{a})、8(\mathrm{b})分别给出了有 / 无承台侧土两种工况下，承台加速度与土面加速度比值的统计结果，蓝色曲线为累计百分比曲线。结果表明，有 / 无承台侧土，承台加速度与土面加速度的平均比值分别为 1.364 和 1.139。针对有承台侧土工况，图8(\mathrm{c})进一步给出了承台惯性力与承台侧土抗力比值的统计结果，平均值为 1.004。

图 9 对有 / 无承台侧土两种工况下，40 条地震记录导致的墩顶、桩顶位移最大值进行了比较。图中纵、横坐标分别为有 / 无侧土工况下的最大位移值，每个点对应一条地震记录。可见，40 条地震记录的反应点基本都位于对角线附近，有 / 无承台侧土两种工况的最大位移比值，墩顶、桩顶的平均比值分别为0.96、0.94。可以说，承台侧土的约束作用减小了结构基本周期，也减小了结构地震位移，但减小幅度可以忽略。

图 10 对有 / 无承台侧土两种工况下，40 条地震记录导致的墩底、桩顶曲率最大值进行了比较。图中纵、横坐标分别为有 / 无侧土工况下的最大曲率值，每个点对应一条地震记录。从图10(\mathrm{a})可知，40 条地震记录的反应点大部分位于对角线上侧，承台侧土的约束作用会明显增大墩底曲率，有侧土与无侧土两种工况的墩底曲率最大值的比值，平均值为 1.23。图10(\mathrm{b})则表明，40 条地震记录的反应点大部分位于对角线下侧，承台侧土的抗力会显著减小桩顶曲率。

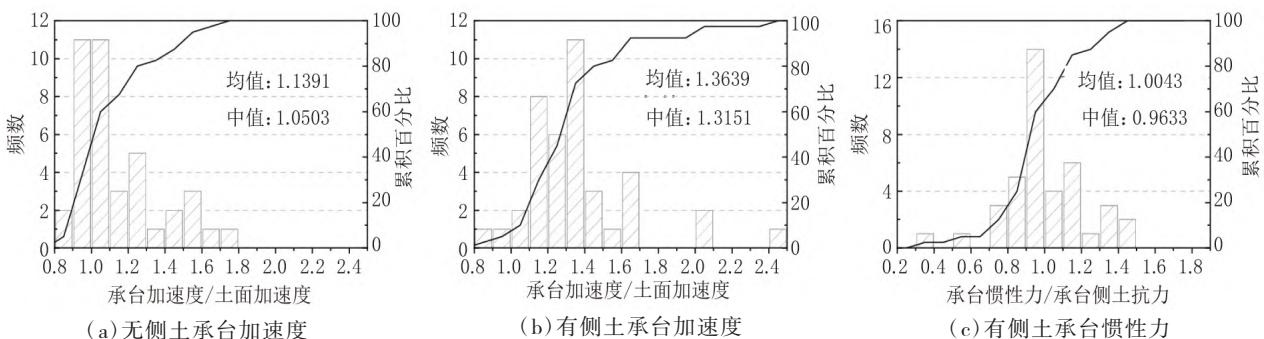
图 8 承台加速度与惯性力统计

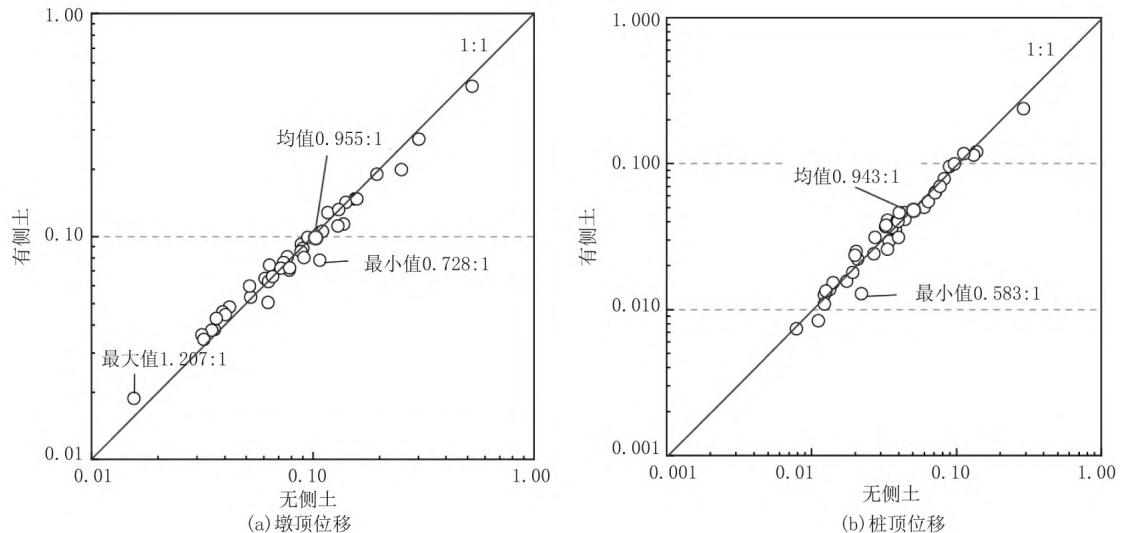
40条波有侧土与无侧土最大位移比较
图 9 40 条波有侧土与无侧土最大位移比较

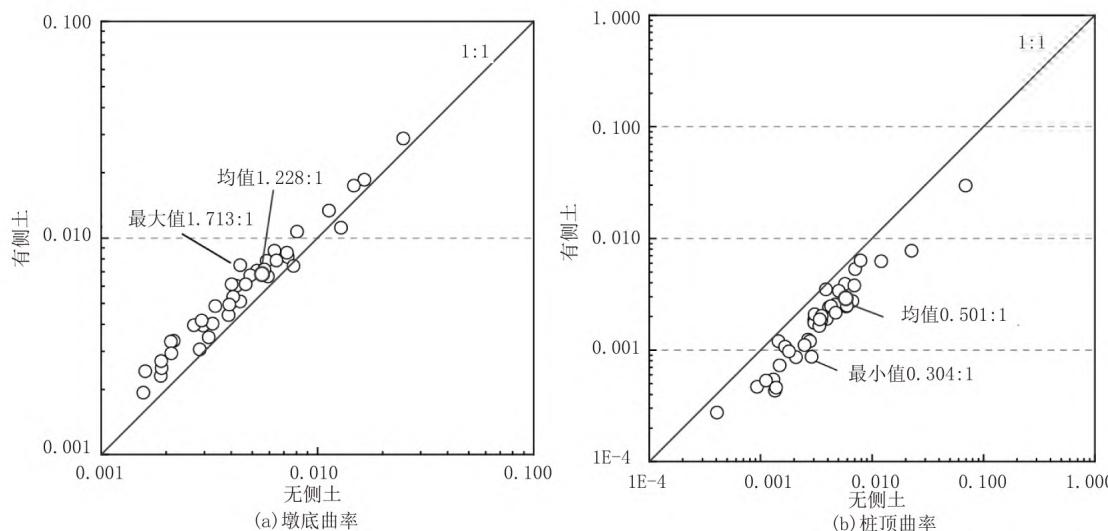
40条波有侧土与无侧土最大曲率比较
图 10 40 条波有侧土与无侧土最大曲率比较

4 结论

本文针对砂土场地典型常规桥梁，采用p - y非线性弹簧模拟土－承台动力相互作用，并建立土 - 桥梁结构一体化模型，采用 40 条实际地震记录进行了地震反应分析。通过对比有 / 无承台侧土两种情况的结构地震反应，研究了土－承台动力相互作用对砂土场地桩基础桥梁地震反应的影响，得出了以下几条结论：

(1) 土－承台动力相互作用会使结构的基本周期减小，从而使墩底曲率明显增大（平均22.8\%），墩顶位移略微减小（平均4.5\%）。因此，不考虑土－承台动力相互作用会低估桥墩的地震反应。

(2) 考虑土－承台动力相互作用后，承台加速度显著大于土面加速度（平均36.4\%），但承台侧土抗力与承台惯性力大小相近（平均 1.004 倍）。因此，在实际工程中，只要计算承台侧土抗力贡献时考虑必要的安全系数，可以假定承台加速度等于土面加速度。

(3) 考虑土－承台动力相互作用后，承台侧被动土压力分担了较大的地震惯性力，因此桩顶曲率大幅减小（平均50\%），不考虑土－承台动力相互作用过于保守。

参考文献

HARABIKA P J, NATH U K. Finite element analysis of pile- soil- cap interaction under lateral load [C]//Imlian Geotechnical Conference- 2010, GEOTrendz December. 2010: 16- 18.
MOHAMED ASHOUR, ASER I ABBAS, SEDAN BOSKOVIC. Pile cap interaction with bridge pile foundations under lateral loads [J]. Journal of Bridge Engineering, 2019, 24(6): 04019053.1- 04019053.14.
张永亮，陈兴冲. 桩－土－承台相互作用对城市曲线匝道桥抗震性能的影响 [J]. 公路交通科技，2012，29（9）：64- 68，76.
RAYCHOWDHURY P, HUTCHINSON T C. Performance evaluation of a nonlinear Winkler - based shallow foundation model using centrifuge test results [J]. Earthquake Engineering & Structural Dynamics,2009,38(5):679- 698. ↩ ↩
JTG3363—2019，公路桥涵地基与基础设计规范 [S]. ↩ ↩
COMARTIN C, NIEWIAROWSKI R, ROJAHN C. ATC- 40 Seismic evaluation and retrofit of concrete buildings[J]. SSC 96,1996,1. ↩
COULOMB C A. Essai sur une application des regles de maximis et minimis a quelques problemes de statique relatifs a l'ar- chitecture[J].Mem.Div.Sav.Acad.,1773,7. ↩
MANDER J, PRIESTLEY M. Theoretical stress- strain model for confined concrete [J]. Journal of Structural Engineering, 1988,114(8):1804- 1826. ↩
WANG X,YE A, JI B. Fragility- based sensitivity analysis on the seismic performance of pile- group- supported bridges in liquefiable ground undergoing scour potentials [J]. Engineering Structures,2019,198(1):109427.1- 109427.15. ↩
O'NEILL M W, MURCHISON J M. An evaluation of py relationships in sands[M]. Houston: University of Houston, 1983. ↩
BAKER J W, LIN T, SHAHI S K, et al. New ground motion selection procedures and selected motions for the PEER transportation research program[J]. PEER report,2011,3. ↩