液化场地桩柱式基础桥梁结构地震反应的敏感性分析
期刊论文

液化场地桩柱式基础桥梁结构地震反应的敏感性分析

王晓伟，叶爱君，罗富元

(同济大学土木工程防灾国家重点实验室，上海 200092)

摘要：地震反应的有效估计是液化场地桥梁结构设计、加固改造的必要环节，但通过数值模拟手段获得的结果易受模型参数变化的影响。为探究影响液化场地桥梁结构地震反应的控制性参数，该文首先建立了某离心机试验的场地 - 结构整体有限元模型，通过数值分析与试验结果的对比验证了数值方法的可靠性；然后，建立了上覆粘土层 - 松砂层 - 密砂层的典型倾斜液化场地 - 桩柱式桥梁结构有限元模型，采用龙卷风图和一次二阶矩方法，以场地和结构的主要物理性质为分析参数，进行场地、结构地震反应的敏感性分析。结果表明：场地、结构的地震反应与各分析参数大体上呈线性或低非线性的变化关系；在所研究的参数中，液化松砂层的内摩擦角、土层倾角和地震峰值加速度为控制性参数，而密砂层各参数和钢筋、混凝土强度参数的敏感性均很低。研究结果可对液化场地桥梁结构地震反应的准确估算，振动台、离心机模型试验的工况优化提供科学参考。

关键词：液化场地；桥梁结构；模型验证；地震反应；敏感性分析

中图分类号：TU473.1 文献标志码：A doi: 10.6052/j.issn.1000-4750.2015.01.0022

SESIMIC RESPONSE SENSITIVITY ANALYSIS OF PILE SUPPORTED BRIDGE STRUCTURES IN LIQUEFIABLE GROUND

WANG Xiao-wei, YE Ai-jun, LUO Fu-yuan

(State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract: Numerical prediction on seismic response of liquefiable soil-structure system is susceptible to varying model input parameters. In order to detect soil parameters that have most significant effects on the seismic response of pile-soil-bridge structure system in liquefiable ground, this paper firstly calibrated the numerical approach by simulating a centrifuge testing. A typical model of pile supported bridge structure embedded into an inclined ground with three layers (overburden clay crust, saturated loose sand and dense sand, respectively) was then established. Sensitivity analysis focused on soil physical properties as well as structural properties. The parameters were the displacement and acceleration of the ground surface, and the displacement of the superstructure. Linear to low-level nonlinear trends between most of the soil parameters and the demands were obtained. The first-order sensitivity analysis indicated that, among the input parameters, the friction angle of loose saturated sand, the ground inclined angle, and PGA has the most significant effect on seismic response of the ground and structure. Sensitivity analysis also revealed the soil parameters with low-level uncertainty. In general, the results of this paper are beneficial supplements for accurately evaluating the seismic response of bridge structures in liquefied and lateral spreading ground as well as the optimal design of the corresponding shaking table tests or centrifuge tests.

Key words: liquefiable ground; bridge structures; model calibration; seismic response; sensitivity analysis

PDF BibTeX

我国沿海、江河地区水网密布，采用桩柱式桥墩基础的中小跨径梁式桥建造广泛，且桥址场地多为软土地基，存在大量潜在液化土层。国内外历次地震震害显示，土体液化及场地侧向大变形导致桥梁结构的严重损伤 1,2。鉴于此，对潜在液化场地的桥梁结构进行抗震性能的评估尤为重要，而完成这项工作的必要环节是对场地及桥梁结构的地震反应做出有效的估算 3,4，但估算的精确程度往往受到模型各参数不确定性的影响，比如某一给定密实度的土体所对应的密度、内摩擦角、剪切模量等参数往往在一定范围内变化 5,6，这不可避免地影响了模型的分析结果。因此，有必要采用基于概率的方法，比较各参数的变化对结构地震反应值增减的贡献程度，即参数敏感性分析。进一步而言，该分析结果可为桥梁结构的设计、加固提供科学依据，并对振动台、离心机模型试验的优化设计提供参考。

针对液化场地桥梁结构的地震反应特性，国内外研究集中于参数分析 7,8,9，即研究了各单一参数对结构地震反应的影响，而未对各参数的影响程度进行比较分析，即很少的研究是参数敏感性分析，而这方面的代表性文献有：Na 等 10 对港口沉箱结构在场地液化下的地震反应进行了参数敏感性分析，发现土体的内摩擦角和剪切模量的变化对结构位移响应的较敏感；Haskell 等 11 研究了液化场地单桩拟静力简化分析方法的参数敏感性；Heidary-Torkamani 等 12 分析了土体参数对码头结构地震响应的敏感性，发现对于不同的响应指标，土体参数的敏感性差别较大；此外，Nour 等 13 对非液化场地桩承海洋钻井平台结构进行了参数敏感性分析，发现与土体参数相比，结构参数对地震响应的敏感性几乎可以忽略。相比之下，针对液化场地桥梁结构地震反应的参数敏感性分析，国内外研究仍缺乏。并且，与沉箱、单桩或码头结构相比，由于桩 - 土 - 上部结构的相互作用，液化场地桥梁结构的动力特性更为复杂，其地震反应的敏感性很值得研究。

本文首先介绍参数敏感性分析的方法及基本原理。然后，建立了某离心机试验的二维场地 - 单桩结构有限元模型，通过数值分析与离心机试验结果的对比，验证了数值模拟方法的可靠性。在此基础上，建立了某典型液化场地 - 桩柱式桥梁结构有限元模型, 以土体、结构的物理性质为敏感性分析参数, 通过比较场地、结构的地震反应值, 分析各参数的敏感性, 获得控制性参数, 并得到相关结论。

1 敏感性分析方法及基本原理

参数敏感性分析主要有三种常用的方法，龙卷风图 (Tornado Diagram)、一次二阶矩(First-Order Second-Moment) 和蒙特卡洛 (Monte Carlo) 方法 14。蒙特卡洛方法通常需大量的样本，考虑到液化场地 - 桥梁结构整体有限元模型的复杂性，该方法计算效率相对较低。故采用龙卷风图和一次二阶矩方法。

1.1 龙卷风图方法

对于满足正态分布的各参数，以相同的概率分布区间为上下界，获得地震反应的变化区间，将该区间按由宽到窄的顺序从上至下排列，形成类似龙卷风形状的图形，即所谓的龙卷风图方法，反应的变化区间越宽，意味着对应参数的敏感性越高。

1.2 一次二阶矩方法

场地或结构的地震反应值 Y 可表述为各随机变量 X_{i}(i = 1,2,\dots ,n) 的函数：

Y = f \left(X _ {1}, X _ {2}, \dots , X _ {n}\right) \tag {1}

假定变量满足正态分布，X_{i}\sim N(\mu_{X_{i}},\sigma_{X_{i}}^{2}) 其中 \mu_{X_i} 、 \sigma_{X_i}^2 分别为各随机变量的均值和方差，则式 (1) 可按照泰勒级数展开为下式：

\begin{array}{l} Y = f \left(\mu_ {X _ {1}}, \mu_ {X _ {2}}, \dots , \mu_ {X _ {n}}\right) + \frac {1}{1 !} \sum_ {i = 1} ^ {n} \left(X _ {i} - \mu_ {X _ {i}}\right) \frac {\partial f}{\partial X _ {i}} + \\ \frac {1}{2 !} \sum_ {j = 1} ^ {n} \sum_ {i = 1} ^ {n} \left(X _ {i} - \mu_ {X _ {i}}\right) \left(X _ {j} - \mu_ {X _ {j}}\right) \frac {\partial^ {2} f}{\partial X _ {i} \partial X _ {j}} + \dots \tag {2} \\ \end{array}

式 (2) 中仅考虑到一次项，而忽略其他高次项，则可简化为：

Y \approx f \left(\mu_ {X _ {1}}, \mu_ {X _ {2}}, \dots , \mu_ {X _ {n}}\right) + \sum_ {i = 1} ^ {n} \left(X _ {i} - \mu_ {X _ {i}}\right) \frac {\partial f}{\partial X _ {i}} \tag {3}

对式 (1) 取均值可得 Y 的均值：

\mu_ {Y} = f \left(\mu_ {X _ {1}}, \mu_ {X _ {2}}, \dots , \mu_ {X _ {n}}\right) \tag {4}

对式 (3) 取二阶矩可得 Y 的方差近似值：

\begin{array}{l} \sigma_ {Y} ^ {2} \approx \sum_ {j = 1} ^ {n} \sum_ {i = 1} ^ {n} \operatorname {C O V} \left(X _ {i}, X _ {j}\right) \frac {\partial f}{\partial X _ {i}} \frac {\partial f}{\partial X _ {j}} \approx \\ \sum_ {i = 1} ^ {n} \sigma_ {X _ {i}} ^ {2} \left(\frac {\partial f}{\partial X _ {i}}\right) ^ {2} + \sum_ {j = 1} ^ {n} \sum_ {i = 1} ^ {n} \rho_ {X _ {i} Y _ {i}} \frac {\partial f}{\partial X _ {i}} \frac {\partial f}{\partial X _ {j}} \tag {5} \\ \end{array}

式中： \mathrm{COV}(X_i, X_j) 为两变量的变异系数； \rho_{X_iY_i} 为不同变量的相关系数，若假定各随机变量是独立的，即 \rho_{X_iY_i} = 0 。于是，式 (5) 可进一步近似为：

\sigma_ {Y} ^ {2} \approx \sum_ {i = 1} ^ {n} \sigma_ {X _ {i}} ^ {2} \left(\frac {\partial f}{\partial X _ {i}}\right) ^ {2} \tag {6}

式 (6) 中偏微分 (\partial f / \partial X_{i}) 可通过有限差分方法求得：

\frac {\partial f \left(X _ {1} , X _ {2} , \cdots , X _ {n}\right)}{\partial X _ {i}} = \frac {f \left(X _ {1} , X _ {2} , \cdots , \mu_ {X _ {i}} + \Delta X _ {i} , \cdots , X _ {n}\right) - f \left(X _ {1} , X _ {2} , \cdots , \mu_ {X _ {i}} - \Delta X _ {i} , \cdots , X _ {n}\right)}{2 \Delta X _ {i}} \tag {7}

式 (7) 中： \Delta X_{i} 为各变量的上下界与均值的距离。进一步可得到各变量对地震反应值变化范围 (\sigma_{Y}^{2}) 的贡献率 R V_{X_{i}} ，该值越大说明变量的敏感性越高。

R V _ {X _ {i}} = \frac {\sigma_ {X _ {i}} ^ {2} \left(\partial f / \partial X _ {i}\right) ^ {2}}{\sigma_ {Y} ^ {2}} \tag {8}

值得一提的是，式 (2)~ 式(3) 的简化过程仅保留线性项，故一次二阶矩法适用于地震反应值随变量呈线性或低非线性的变化 15。

2 数值分析方法及可靠性验证

2.1 离心机试验

为研究桩基础在液化场地的地震反应特性，Wilson 等 15 进行了离心机模型试验。以工况 CSP3 的单桩试件为研究对象，其原型构造、土体参数 ( 重度 \gamma 、相对密度 D_{\mathrm{r}} 和内摩擦角 \varphi ) 及部分测点布置如图 1 所示，桩身弹性模量为 7\times 10^{7}\mathrm{kPa}。

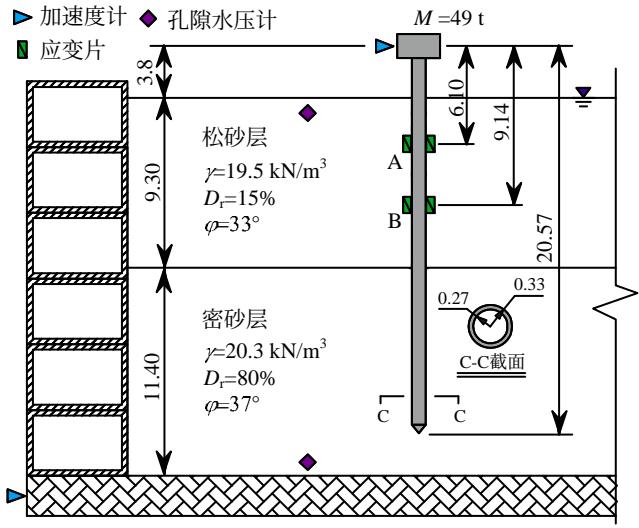
图1CSP3离心机试验布置 15
图 1CSP3 离心机试验布置 15
Fig.1 Layout of the model for CSP3 centrifuge test 15

2.2 液化场地桩-土-结构整体化模拟方法

采用开源平台 OpenSees 16, 建立上述离心机试验的桩 - 土 - 结构整体有限元模型。

2.2.1 饱和土体动力数值方程

基于 Biot 土 - 水耦合作用理论 17,18，采用忽略水的平均相对加速度的 U - P 公式（ U 为土体位移， P 为孔隙水压），该公式可较好模拟动载作用下饱和土已得到较广泛应用 19,20,21。 U - P 公式的大致代数形式 22：

\boldsymbol {M} \ddot {\boldsymbol {U}} + \int_ {V} \boldsymbol {B} ^ {\mathrm {T}} \boldsymbol {\sigma} ^ {\prime} \mathrm {d} V - Q \boldsymbol {P} - \boldsymbol {f} ^ {(\mathrm {s})} = 0 \tag {9}
\boldsymbol {Q} ^ {\mathrm {T}} \dot {\boldsymbol {U}} + \boldsymbol {H} \boldsymbol {P} + \boldsymbol {S} \dot {\boldsymbol {P}} - \boldsymbol {f} ^ {(\mathrm {p})} = 0 \tag {10}

式中： M 为质量矩阵； U 为位移向量； B 为应变 - 位移矩阵； \sigma' 为有效应力张量； Q 为土颗粒 - 水耦合离散梯度算子； P 为孔隙水压向量； S 为压缩系数矩阵； H 为渗透系数矩阵。向量 f^{(\mathrm{s})} 和 f^{(\mathrm{p})} 分别为土颗粒、水的体力及边界条件。动力体系的阻尼效应通过引入瑞利阻尼考虑。

2.2.2 材料本构

砂土的模拟采用对孔隙水压变化敏感的多屈服面塑性材料 23,24，对应于 OpenSees 材料库中的 PDMY 材料 16，该材料可模拟砂土在循环荷载作用下出现的剪胀、流动等现象。粘土的模拟采用对孔隙水压变化不敏感的多屈服面塑性材料 25,26，即孔隙水压的变化对土体剪切特性的影响较小，对应于 OpenSees 材料库中的 PIMY 材料 16。土体材料本构的具体介绍可参见文献 23,24,25,26。此外，由于离心机试验中结构始终保持弹性状态，因此桩身的模拟采用弹性梁柱单元。

2.2.3 桩-土相互作用

桩 - 土相互作用的模拟采用考虑土体液化影响的 p - y 弹簧本构 27 ( p 代表桩 - 土相互作用力， y 代表桩 - 土水平相对位移 )，弹簧的极限强度 p_{\mathrm{u\_liq}} 随场地液化的加深而减小至某残余强度 p_{\mathrm{res}} 。

p _ {\mathrm {u} \_ \text {l i q}} = p _ {\text {r e s}} + (p _ {\mathrm {u}} - p _ {\text {r e s}}) \frac {\sigma_ {\mathrm {t}} ^ {\prime}}{\sigma_ {0} ^ {\prime}} = p _ {\mathrm {u}} \left(1 - r _ {\mathrm {u}}\right) + p _ {\mathrm {r e s}} r _ {\mathrm {u}} \tag {11}

式中： p_{\mathrm{u}} 为不考虑液化的桩土相互作用力； \sigma_{\mathrm{t}}' 和 \sigma_{0}^{\prime} 分别为土体单元的实时、初始平均有效应力； r_{\mathrm{u}} 为超孔隙水压比，该值越大说明液化程度越高。

r _ {\mathrm {u}} = 1 - \frac {\sigma_ {\mathrm {t}} ^ {\prime}}{\sigma_ {0} ^ {\prime}} \tag {12}

对于砂土， p_{\mathrm{u}} 取以下两公式的较小值 28：

p _ {\mathrm {u s}} = \left(c _ {1} h + c _ {2} d\right) h \gamma^ {\prime} \tag {13a}
p _ {\mathrm {u d}} = c _ {3} d h \gamma^ {\prime} \tag {13b}

式中： p_{\mathrm{us}} 和 p_{\mathrm{ud}} 分别为不液化时浅层、深层土体的极限抗力； h 为 p-y 弹簧的深度； d 为桩径； \gamma' 为土的有效容重；系数 c_1 、 c_2 和 c_3 由图 2 29 确定。桩 - 砂土相互作用的数学表达式：

p = A p _ {\mathrm {u} _ {-} \mathrm {l i q}} \tanh \left(\frac {n _ {\mathrm {h}} h y}{A p _ {\mathrm {u} _ {-} \mathrm {l i q}}}\right) \tag {14}

式中： A 为荷载系数，对于循环荷载取 0.9 ； n_{\mathrm{h}} 为地基弹性模量，可通过图 3 29 确定。

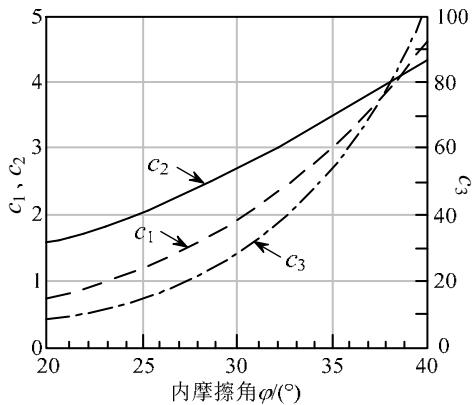
图2系数 c_{1} 、 c_{2} 和 c_{3} 与内摩擦角关系 29
图 2 系数 c_{1} 、 c_{2} 和 c_{3} 与内摩擦角关系 29
Fig.2 Coefficients c_{1}, c_{2} and c_{3} versus friction angle 29

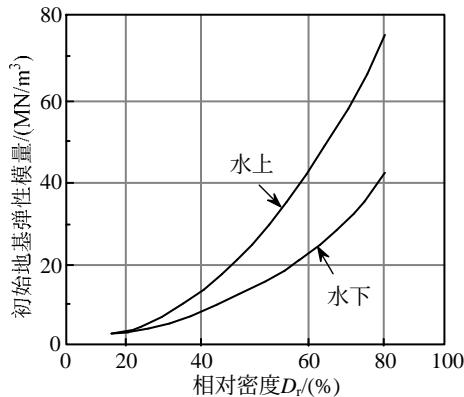
图3 砂土初始地基弹性模量与相对密度关系 29
图 3 砂土初始地基弹性模量与相对密度关系 29
Fig.3 Initial subgrade coefficient of cohesionless soils versus relative density 29

对于粘土，由于地震下一般不会发生液化，故可直接采用不考虑液化影响的 p - y 弹簧本构 28。粘土的极限强度 29：

p _ {\mathrm {u}} = \left\{ \begin{array}{l l} 3 s _ {\mathrm {u}} + \gamma^ {\prime} h + J s _ {\mathrm {u}} h / d, & h \leq h _ {\mathrm {r}} \\ 9 s _ {\mathrm {u}}, & h > h _ {\mathrm {r}} \end{array} \right. \tag {15a}
h _ {\mathrm {r}} = \frac {6 s _ {\mathrm {u}} d}{\gamma^ {\prime} d + J s _ {\mathrm {u}}} \tag {15b}

式中： s_{\mathrm{u}} 为粘土不排水剪切强度； J 为无量纲系数，通常取 0.5。桩 - 粘土相互作用的数学表达式：

p = \frac {1}{2} p _ {\mathrm {u}} \left(\frac {y}{2 . 5 d \varepsilon_ {5 0}}\right) ^ {1 / 3} \tag {16}

式中： \varepsilon_{50} 为 50\% 的最大主应力差对应的应变；软、中、硬粘土分别取 0.02、0.01、0.005。

2.2.4 离心机试验数值模型

离心机试验的数值分析模型如图 4。地震下土体有效应力的变化 (即孔隙水压的变化) 传递给与之相连的 p - y 弹簧，其中 p_{\mathrm{res}} = 0.3p_{\mathrm{u\_liq}} 。模型边界条件：基底和桩底约束平动自由度，两侧边界共用水平自由度，以模拟离心机剪切箱；基底及两侧边界土体不排水，顶层土体可排水。值得一提的是，在模拟桩 - 土相互作用时，仅考虑了水平向的 p - y 弹簧，并没有考虑竖向的 t - z 、 q - z 弹簧（ t 为桩身摩擦力， q 为桩底压力， z 为桩 - 土竖向相对位移），主要是因为单桩不具备群桩所特有的摇摆效应 (类似框架结构)，故桩 - 土相互作用应以水平向为主。

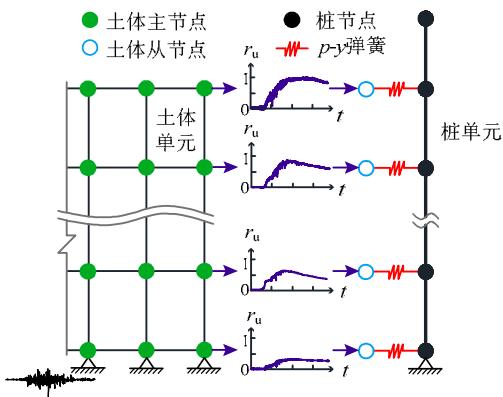
图4 数值分析模型图示
图 4 数值分析模型图示
Fig.4 Numerical model

2.3 数值方法可靠性验证

以峰值加速度 (PGA) 为 0.5 \mathrm{~g} 的 Santa Cruz 波为地震输入，进行非线性时程反应分析，数值分析与试验结果对比见图 5。总体而言，本文所采用的数值方法可有效模拟土体和桩基桥梁结构的地震反应，即验证了数值方法的可靠性 15。

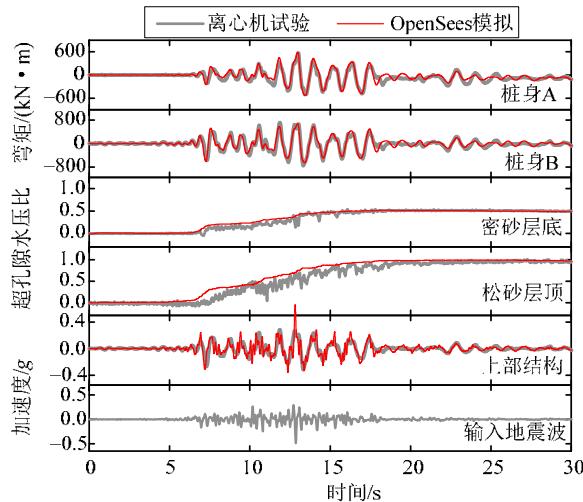
图5数值分析与离心机试验结果 15 时程对比
图 5 数值分析与离心机试验结果 15 时程对比
Fig.5 Comparison of time histories between numerical analysis and the centrifuge test 15

3 地震反应敏感性分析

3.1 液化场地-桥梁结构模型

为研究液化场地桥梁结构地震反应的控制性参数，在对已建中小跨径桥梁调研的基础上，建立了某典型三层土倾斜场地 - 桩柱式基础 - 上部结构有限元模型，见图 6。桩柱式墩截面直径 d = 1.8\mathrm{m} ，截面配筋率 2\% ，桩基埋深 32.4\mathrm{m}(18d) ，墩高 8\mathrm{m} ，上部结构质量 830\mathrm{t} 。土层分布自上而下分别为 8.1\mathrm{m} 的粘土层、 10.8\mathrm{m} 的松砂层和 13.5\mathrm{m} 的密砂层，桩身采用纤维截面 - 非线性梁柱单元，钢筋采用 Menegotto-Pinto 本构 30，混凝土采用 Kent-Park 本构 31，材料的滞回特性见图 6。模型的边界条件同离心机试验模型。

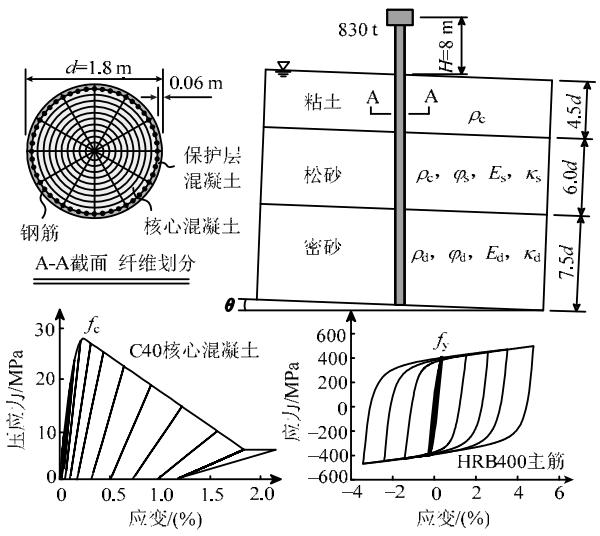
图6 倾斜液化场地-桩柱式桥墩-上部结构模型
图 6 倾斜液化场地 - 桩柱式桥墩 - 上部结构模型
Fig.6 Model of pile in inclined liquefiable ground

3.2 土体和结构的敏感性分析参数

为考察土体、结构材料的不确定性对地震反应的影响，以粘土的密度，松砂、密砂层的内摩擦角、剪切模量、渗透系数以及土层的倾角为土体的敏感性分析参数，如图 6 所示；结构材料的敏感性分析参数为钢筋的屈服强度和混凝土的抗压强度。

以 s_{\mathrm{u}} \approx 50 \mathrm{kPa} 的中性粘土、 D_{\mathrm{r}} \approx 40\% 的松砂和 D_{\mathrm{r}} \approx 80\% 的密砂所对应的土性为均值 \mu_{X} 32，根据各参数的变异系数 \mathrm{COV} = \sigma_{X} / \mu_{X} 12,33,34，取 \mu_{X} \pm \sigma_{X} 和 \mu_{X} \pm 2\sigma_{X} ，即每个参数取 5 个值，用于分析地震反应随各参数的变化规律，考察是否满足线性 (或低非线性) 规律。而敏感性分析以 \mu_{X} \pm \sigma_{X} 为各参数的上下界进行。土体和结构参数的不确定性见表 1，各参数具体取值见表 2。

表 1 土体和结构敏感性分析参数的变异系数
Table 1 COV values of soil and structure parameters for sensitivity analysis

参数 对象 符号 COV=σX/μX
土体密度/(g/cm³) 粘土 \rho_c 0.09
松砂 \rho_s 0.09
密砂 \rho_d 0.09
土体内摩擦角/(°) 松砂 \varphi_s 0.09
密砂 \varphi_d 0.09
土体剪切模量/kPa 松砂 E_s 0.12
密砂 E_d 0.12
土体渗透系数/(m/s) 松砂 \kappa_s 0.30
密砂 \kappa_d 0.30
土层倾角 所有 \theta 0.33
钢筋屈服强度/MPa 主筋 f_y 0.20
混凝土抗压强度/MPa 核心 f_c 0.20

表 2 土体和结构敏感性分析参数的取值
Table 2 Soil and structure parameter matrix considered in the sensitivity analysis

参数变化 粘土 松砂 密砂 土层倾角 结构
\rho_c/(g/cm³) \rho_s/(g/cm³) \varphi_s(°) E_s/kPa \kappa_s/(m/s)
\mu_X-2\sigma_X 1.64 1.48 26.24 53200 2.20\times 10^{-4}
\mu_X-\sigma_X 1.82 1.64 29.12 61600 3.50\times 10^{-4}
\mu_X 2.00 1.80 32.00 70000 5.00\times 10^{-4}
\mu_X+\sigma_X 2.18 1.96 34.88 78400 6.50\times 10^{-4}
\mu_X+2\sigma_X 2.36 2.12 37.76 86800 8.00\times 10^{-4}

3.3 地震动输入的敏感性分析参数

仅考虑水平地震作用，以 5 条实际地震记录作为输入，各条波的 PGA 调整为 0.4g ，作为 PGA 的均值 \mu_{X} ，对应的加速度谱见图 7，输入地震波的特征参数见表 3。此外，为分析 PGA 对地震反应的敏感性，取 PGA 变异系数为 0.18 35，分别研究 PGA=0.256 g、0.328 g、0.4 g、0.472 g 和 0.544 g 下各参数取均值 \mu_{X} 对应工况的地震反应值。

以粘土层顶的水平位移、加速度最大值，上部结构的水平位移最大值作为地震反应比较值。以表 2 中各参数的均值 \mu_{X} 为基本工况，逐次改变某一变量，进行该工况在 5 条地震波下的非线性时程反应分析，并对地震反应值取平均值。总共进行 13 \times 5 \times 5 = 325 个工况。

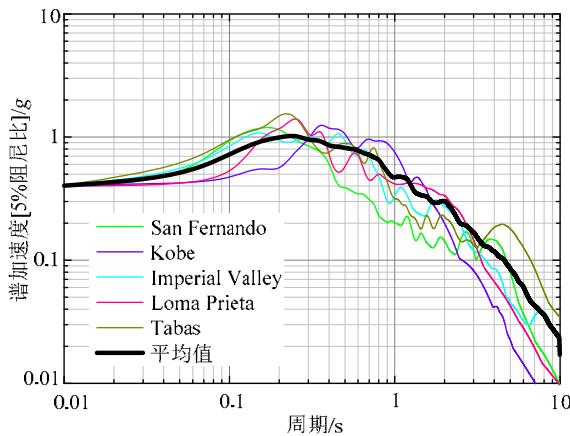
图7 \mathrm{PGA} = 0.4\mathrm{g} 地震波的加速度谱
图 7 \mathrm{PGA} = 0.4\mathrm{g} 地震波的加速度谱

表 3 \mathrm{{PGA}} = {0.4}\mathrm{\;g} 地震波特征参数
Table 3 Characteristics of ground motions with PGA=0.4 g

地震波 原始 PGA/g PGA调整 系数 特征 周期/s 峰值 速度/(cm/s) Arias 强度/(m/s)
San Fernando 0.185 2.16 0.16 31.02 1.91
Kobe 0.228 1.75 0.34 40.64 2.10
Imperial Valley 0.315 1.27 0.14 39.97 2.04
Loma Prieta 0.367 1.09 0.22 48.72 1.60
Tabas 0.852 0.47 0.20 56.91 2.54

4 结果与讨论

4.1 场地、结构地震反应规律

图 8 给出了 San Fernando 地震下基本工况在 10s 时土层的超孔隙水压比和变形情况，此时松砂层顶已液化，上覆粘土层发生了侧向变形。

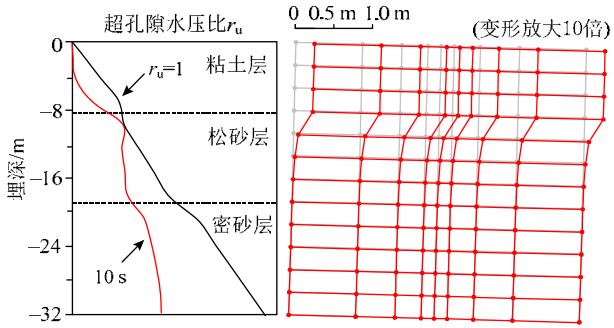
图8 基本工况的超孔隙水压比及土层变形示意
图 8 基本工况的超孔隙水压比及土层变形示意
Fig.8 Schematic of excess pore pressure profiles and deformation mesh for the case with mean values

为考察比较各变量与不同地震反应值的变化规律，对每个变量的 5 个不同取值进行归一化处理：

R ^ {*} \left(\mu_ {X} \pm n \sigma_ {X}\right) = \frac {R \left(\mu_ {X} \pm n \sigma_ {X}\right)}{R \left(\mu_ {X}\right)}, n = 1, 2 \tag {17}

式中： R(\cdot) 为各参数对应工况的地震反应值； R^{*}(\cdot) 则为对应的归一化反应结果。

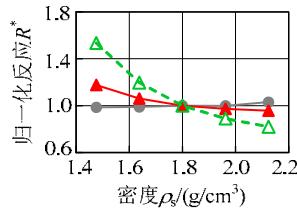
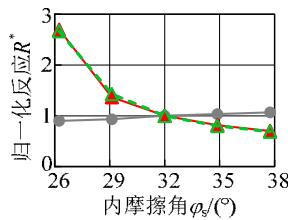
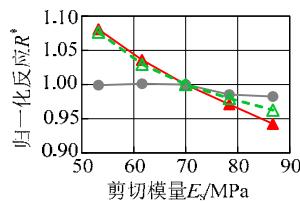
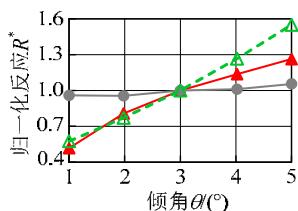
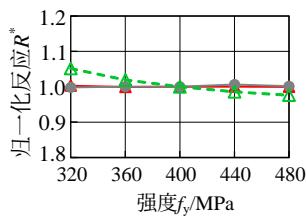
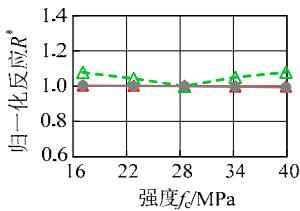
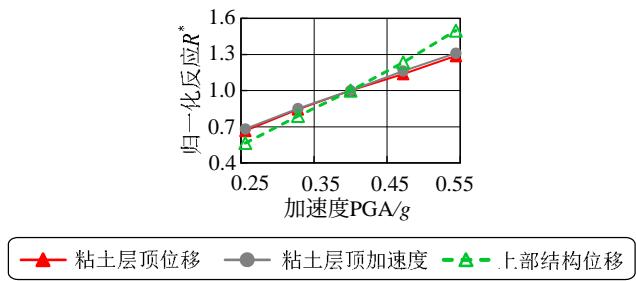
图 9 给出了各敏感性分析变量与归一化结果的变化关系。粘土层的密度、松砂层各参数、土层倾角、钢筋屈服强度、混凝土抗压强度与地震反应呈现比较明显的线性或低非线性的变化规律；对于密砂层各参数，地震反应变化范围均很小，说明密砂层的参数对地震反应不敏感。另一方面，比较图 9 中不同地震反应可知，位移反应的敏感性高于加速度反应。总体上，各参数与土体、结构的地震反应呈现线性或低非线性的变化关系，说明本文采用的敏感性分析方法对所研究的参数是适用的。

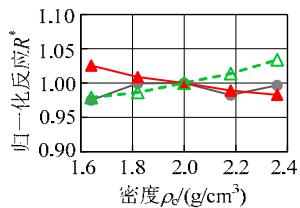
图9 地震反应随各参数的变化规律
图 9 地震反应随各参数的变化规律
Fig.9 Variation of normalized demands with different parameters

粘土层顶位移 粘土层顶加速度 \Delta 上部结构位移
(a) 粘土层密度

粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(b) 松砂层密度

粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(c) 松砂层内摩擦角

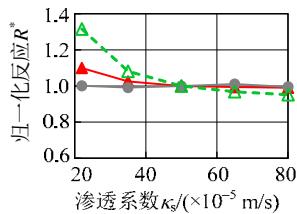
粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(d) 松砂层剪切模量

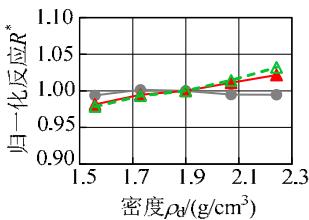
粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(e) 松砂层渗透系数

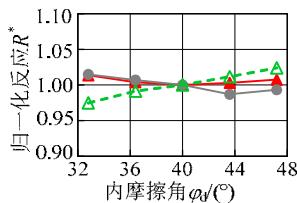
粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(f) 密砂层密度

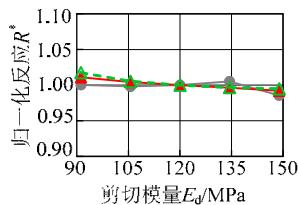
粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(g) 密砂层内摩擦角

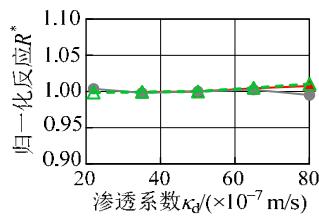
粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(h) 密砂层剪切模量

粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(i) 密砂层渗透系数

粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(j) 土层倾角

粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(k) 钢筋屈服强度

粘土层顶位移 粘土层顶加速度 -\Delta 上部结构位移
(l) 混凝土抗压强度

(m) PGA

4.2 敏感性分析结果

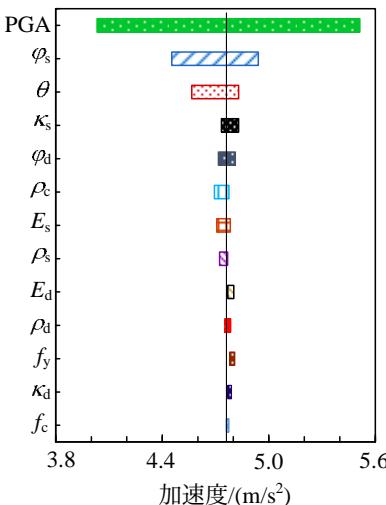
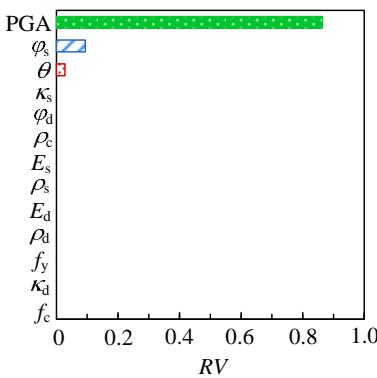
以 \mu_{X} \pm \sigma_{X} 为各参数的上下界，分别采用龙卷风图和一次二阶矩法进行敏感性分析。图 10 给出了不同地震反应的龙卷风图，图中竖线代表基本工况的地震反应。图 11 给出了一次二阶矩的分析结果。总体而言，松砂层的内摩擦角 \varphi_{\mathrm{s}} 、土层倾角 \theta 和 PGA 是场地、结构地震反应的控制性参数。具体而言：1）对于粘土层顶的水平位移，松砂层各参数的敏感性高于上覆粘土层的密度和密砂层各参数；控制参数 \varphi_{\mathrm{s}} 、PGA 和 \theta 对反应方差的贡献分别达 59\% 、 21\% 和 17\% ；而钢筋和混凝土的强度敏感性很低。2）对于粘土层顶水平加速度，控制参数为 PGA 和 \varphi_{\mathrm{s}} ，对地震反应方差的贡献分别为 86\% 和 9.4\% ，其他参数的敏感性很低。3）对于上部结构水平位移，控制性参数为 \varphi_{\mathrm{s}} 、 \theta 、PGA、 \rho_{\mathrm{s}} ，对反应方差的贡献分别为 42\% 、 26\% 、 21\% 、 10\% 而钢筋、混凝土以及密砂层各参数的敏感性较低。上部结构水平位移与土层顶位移的敏感性分析结果相似，说明结构的水平位移主要是由上覆粘土层的侧向大变形引起的。另外，松砂层各参数的敏感性高于上覆粘土层密度，更高于密砂层各参数。

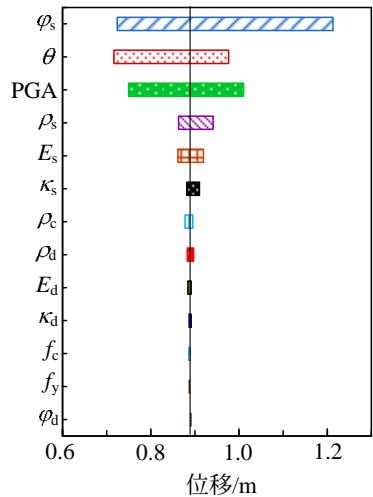
图10 不同地震反应的龙卷风图
图 10 不同地震反应的龙卷风图
Fig.10 Tornado diagram for different demand parameters

粘土层顶位移 粘土层顶加速度 \Delta 上部结构位移
(a) 粘土层顶水平位移

粘土层顶位移 粘土层顶加速度 \Delta 上部结构位移
(b) 粘土层顶水平加速度

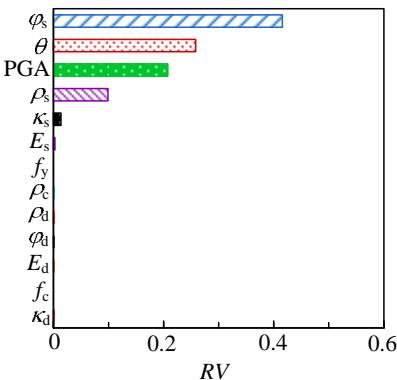
粘土层顶位移 粘土层顶加速度 \Delta 上部结构位移
(c) 上部结构水平位移

图 11 各变量的相对方差贡献值 RV
Fig.11 Relative variance contribution for different demand parameters

5 结论

本文通过对离心机试验的数值模拟，验证了液化场地 - 桥梁结构地震反应模拟方法的可靠性。在此基础上，针对典型三层土液化场地，建立场地 - 桥梁结构有限元模型，以土体材料、土层倾角、结构材料和地震动强度为分析参数，采用龙卷风图和一次二阶矩方法进行参数敏感性分析。针对文中分析的各参数，得到以下结论：

(1) 土层各参数 (密度、内摩擦角、剪切模量、渗透系数、倾角) 以及钢筋屈服强度、混凝土抗压强度与场地、结构的地震反应呈线性或低非线性的关系，龙卷风图和一次二阶矩方法适用于对本文所研究的参数进行地震反应敏感性分析。

(2) 具有上覆非液化土层的倾斜液化场地，桩身及上部结构的侧向变形主要由上覆土层的侧向变形所引起。
(3) 液化松砂层的内摩擦角、土层倾角和 PGA 为场地、结构地震反应的控制性参数，而非液化密砂层和上覆粘土层的参数敏感性均较低。对于液化场地桥梁结构的设计、加固，振动台、离心机试验的工况优化，可重点考虑改变上述控制性参数。

参考文献：

  1. Lin S, Tseng Y, Chiang C, et al. Damage of piles caused by lateral spreading—back study of three cases [C]// Seismic Performance and Simulation of Pile Foundations in Liquefied and Laterally Spreading Ground. CA: ASCE, 2006: 121-133. ↩

  2. Bhattacharya S, Tokimitsu K, Goda K, et al. Collapse of Showa Bridge during 1964 Niigata earthquake: A quantitative reappraisal on the failure mechanisms [J]. Soil Dynamics and Earthquake Engineering, 2014, 65: 55-71. ↩

  3. 黄雨，八屿厚，沢田和秀，等. 堤防地基地震液化的数值模拟 [J]. 工程力学, 2007, 24(12): 82-87.
    Huang Yu, Yashima A, Sawada K, et al. Numerical modeling of earthquake liquefaction in earth embankment foundations [J]. Engineering Mechanics, 2007, 24(12): 82-87. (in Chinese) ↩

  4. 何剑平, 陈卫忠. 桩土复合地基抗液化数值试验分析 [J]. 工程力学, 2012, 29(11): 175-182.
    He Jianping, Chen Weizhong. The numerical experiments and analysis on anti-liquefaction effect of pile-soil composite foundation [J]. Engineering Mechanics, 2012, 29(11): 175—182. (in Chinese) ↩

  5. 陈希哲. 土力学地基基础 [M]. 第 4 版. 北京：清华大学出版社，2004:40—66.
    Chen Xizhe. Soil mechanics and geotechnical engineering [M]. 4th ed. Beijing: Tsinghua University Press, 2004: 40-66. (in Chinese) ↩

  6. Electric Power Research Institute. Manual on estimating soil properties for foundation design [M]. Palo Alto, CA: EPRI, 1990: Chapter 2, 1-39. ↩

  7. Tang L, Maulab, Ling X, et al. Numerical simulations of shake-table experiment for dynamic soil-pile-structure interaction in liquefiable soils [J]. Earthquake Engineering and Engineering Vibration, 2014, 13(1): 171-180. ↩

  8. Valsamis A, Bouckovalas G, Chaloulos Y. Parametric analysis of single pile response in laterally spreading ground [J]. Soil Dynamics and Earthquake Engineering, 2012, 34: 99-110. ↩

  9. Rahmani A, Pak A. Dynamic behavior of pile foundations under cyclic loading in liquefiable soils [J]. Computers and Geotechnics, 2012, 40(3): 114-126. ↩

  10. Na U J, Chaudhuri S R, Shinozuka M. Probabilistic assessment for seismic performance of port structures [J]. Soil Dynamics and Earthquake Engineering, 2008, 28(2): 147-158. ↩

  11. Haskell J J M, Cubrinovski M, Bradley B A. Sensitivity analysis and its role in pseudo-static design of pile foundations [J]. Soil Dynamics and Earthquake Engineering, 2012, 42: 80-94. ↩

  12. Heidary-Torkamani H, Bargi K, Amirabadi R, et al. Fragility estimation and sensitivity analysis of an idealized pile-supported wharf with batter piles [J]. Soil Dynamics and Earthquake Engineering, 2014, 61/62: 92-106. ↩ ↩

  13. Nour E M, Kim J. Sensitivity analysis of pile-founded fixed steel jacket platforms subjected to seismic loads [J]. Ocean Engineering, 2014, 85: 1-11. ↩

  14. Lee T H, Mosalam K M. Probabilistic seismic evaluation of reinforced concrete structural components and systems [R]. CA: Pacific Earthquake Engineering Research Center, 2006. ↩

  15. Wilson D, Boulanger R, Kutter B. Soil-pile-superstructure interaction at soft or liquefiable soils sites — Centrifuge data report for CSP3 [R]. CA: University of California, Davis, 1997. ↩ ↩ ↩ ↩ ↩ ↩ ↩ ↩ ↩

  16. Mckenna F, Fenves G, Scott M, et al. Open system for earthquake engineering simulation. [CP]. CA: University of California, Berkeley, 2001-8-20. ↩ ↩ ↩

  17. Biot M, Theory of elasticity and consolidation for a porous anisotropic solid [J]. Journal of Applied Physics, 1955, 26(2): 182-185. ↩

  18. Zienkiewicz O C, Shiomi T. Dynamic behavior of saturated porous media: the generalized Biot formulation and its numerical solution [J]. International Journal for Numerical Methods in Engineering, 1984, 8(1): 71-96. ↩

  19. Lu J. Parallel finite element modeling of earthquake site response and liquefaction [D]. La Jolla: University of California at San Diego, 2006. ↩

  20. 唐亮，凌贤长，苏雷，等. 液液化场地桥梁群桩基动力反应三维有限元模拟方法 [J]. 岩土工程学报，2013, 35(增刊 2):401—407.
    Tang Liang, Ling Xianzhang, Su Lei, et al. Numerical simulation of dynamic response for pile groups of bridges in liquefiable soils [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Suppl 2):401—407. (in Chinese) ↩

  21. Chan A H C. A unified finite element solution to static and dynamic problems of geomechanics [D]. Swansea, UK: University of Wales, 1988. ↩

  22. Jeremic B. Development of geotechnical capabilities in OpenSees [R]. CA: Pacific Earthquake Engineering Center, 2001. ↩

  23. Elgamal A, Yang Z, Parra E. Computational modeling of cyclic mobility and post-liquefaction site response [J]. Soil Dynamics and Earthquake Engineering, 2002, 22(4): 259-271. ↩ ↩

  24. Yang Z, Elgamal A, Parra E. Computational model for cyclic mobility and associated shear deformation [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 1119-1127. ↩ ↩

  25. Parra E. Numerical modeling of liquefaction and lateral ground deformation including cyclic mobility and dilation response in soil systems [D]. NY: Rensselaer Polytechnic Institute, 1996. ↩ ↩

  26. 唐亮, 凌贤长, 徐鹏举, 等. 液化场地桩 - 土地震相互作用振动台试验数值模拟 [J]. 土木工程学报, 2012, 45(增刊 1):302-306.
    Tang Liang, Ling Xianzhang, Xu Pengju, et al. Numerical simulation of shaking table test for seismic soil-pile interaction in liquefying ground [J]. China Civil Engineering Journal, 2012, 45(Suppl 1): 302-306. (in Chinese) ↩ ↩

  27. Brandenberg S, Zhao M, Boulanger R, et al. p - y plasticity model for nonlinear dynamic analysis of piles in liquefiable soil [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(8): 1262-1274. ↩

  28. Boulanger R, Curras C, Kutter B, et al. Seismic soil-pile-structure interaction experiments and analyses [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(9): 750-759. ↩ ↩

  29. API. Recommended practice for planning, designing, and constructing fixed offshore platforms—Working stress design, 21th ed, API RP2A-WSD [S]. Washington, D C: American Petroleum Institute, 2005. ↩ ↩ ↩ ↩ ↩ ↩ ↩ ↩ ↩

  30. Filippou F C, Popov E P, Bertero V V. Effects of bond deterioration on hysteretic behavior of reinforced concrete joints [R]. Berkeley, CA: Earthquake Engineering Research Center, 1983. ↩

  31. Kent D C, Park R. Flextural members with confined concrete [J]. Journal of the Structural Division, 1971, 97(7): 1969-1990. ↩

  32. Yang Z. Numerical modeling of earthquake site response including dilation and liquefaction [D]. New York: Columbia University, 2000. ↩

  33. Jones A, Kramer S, Arduino P. Estimation of uncertainty in geotechnical properties for performance-based earthquake engineering [R]. CA: Pacific Earthquake Engineering Center, 2002. ↩

  34. Pang Y, Wu X, Shen G, et al. Seismic fragility analysis of cable-stayed bridges considering different sources of uncertainties [J]. Journal of Bridge Engineering, 2014, 19(4): 04013015. ↩

  35. 潘华. 概率地震危险性分析中参数不确定性研究 [D]. 北京：中国地震局地球物理研究所，2000.
    Pan Hua. Study on uncertainties in the parameters of PSHA [D]. Beijing: Institute of Geophysics, China Earthquake Administration, 2000. (in Chinese) ↩

评论
Copyright © 2025 桥梁抗震小站 All Rights Reserved. Powered by Halo.