PDF BibTeX

---

0 引言

小箱梁桥在中小跨度梁式桥中的应用已经非常广泛，一般在墩、梁间设置板式橡胶支座承担竖向力，同时在盖梁两端设置混凝土挡块来防止横向落梁震害。然而，2008 年汶川大地震中¹，大量采用板式橡胶支座和混凝土挡块组合抗震的梁式桥发生了支座脱落和移位震害，造成混凝土挡块和相连盖梁破坏严重，甚至发生落梁震害。因此，有必要对小箱梁桥的横向减震体系进行深入研究，以提高桥梁的抗震性能。

利用支承连接装置耗能的减震体系是国内外桥梁抗震设计规范推荐的 2 种抗震结构体系之一。对于板式橡胶支座梁桥，中国《公路桥梁抗震设计细则》（JTG/T B02-01—2008）和《城市桥梁抗震设计规范》（CJJ 166—2011）中一般不允许支座发生滑动，仅利用其柔性抗震，同时要求横桥向设置抗震挡块。然而，对于横向挡块的设计和设置方式，各国规范仅给出了指导性的规定。美国规范²对挡块提出了两水准的性能要求，即在多遇地震下保持弹性，在设计地震下设计为牺牲构件。中国桥梁抗震设计规范仅把挡块作为抗震设防措施，没有给出相应的设计方法和间隙设置方式。于是，不少学者开展了桥梁抗震挡块方面的研究。Silva 等³针对混凝土挡块提出了简化的力学计算模型；徐略勤等⁴,⁵开展了混凝土挡块的抗震性能研究，提出了不同的破坏模型；李建中等⁶,⁷针对简支梁桥，提出了板式橡胶支座与 X 形弹塑性挡块联合使用的横桥向隔震系统，进行了挡块力学参数的分析，给出了关键影响参数的建议取值，进行了振动台试验，与横桥向无约束自由滑动体系对比，证明了弹塑性挡块能够有效控制墩梁相对位移和传递到下部结构的梁体地震力。另一方面，中国桥梁抗震设计规范推荐了 3 种分离型减隔震装置，橡胶支座与金属阻尼器组合是其中之一，只是需要有合适的金属阻尼器。经过几十年的研究，已开发的金属阻尼器构造形式已多达十几种⁸，其中，E 形钢阻尼器⁹、C 形钢阻尼器¹⁰等都在桥梁上得到了许多应用。然而，当金属阻尼器应用于桥梁横向减震时，需要适应桥梁的纵向变形。沈星等¹¹,¹²基于三角形钢板，采用球形传力键适应地震下复杂接触条件，提出了一种适用于桥梁横向的钢阻尼器，并通过拟静力试验证明了阻尼器具有很好的滞回耗能特性。因此，在板式橡胶支座梁桥中，可以采用设置钢阻尼器和钢挡块 2 种方式来改善桥梁的抗震性能，只是在钢阻尼器和钢挡块的结构形式、设置方式及参数方面，还需要结合不同的主梁形式进一步研究，而对于 2 种体系的耗能特性研究，则更加缺乏。

本文将根据小箱梁桥的构造特点，以文献¹¹的横向钢阻尼器为基础，首先提出板式橡胶支座与钢阻尼器组合（后面简称“钢阻尼器体系”）、板式橡胶支座与钢挡块组合（后面简称“钢挡块体系”）2 种横桥向减震体系，阐明体系的力学特性，并提出主要参数的确定方法；然后建立典型简支小箱梁桥的单墩模型，对 2 种减震体系结构的地震反应进行时程反应分析，并着重对 2 种减震体系的耗能特性进行深入分析。

1 两种减震体系及其力学特性

1.1 减震体系的组成及力学特性

1.1.1 钢阻尼器体系

钢阻尼器体系由板式橡胶支座和钢阻尼器组成，如图 1 所示。

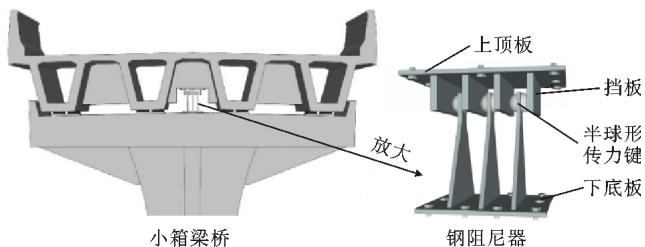
图 1 钢阻尼器体系示意

其中，板式橡胶支座采用常规方法设置在小箱梁底，承担桥梁竖向荷载，地震时允许滑动并和钢阻尼器共同耗能减震。钢阻尼器¹¹设置在桥墩中心位置，由上、下两部分组成：上半部分用螺栓铆接在梁底（横隔板处），由上顶板和设置了聚四氟乙烯滑板的钢挡板组成；下半部分用螺栓铆接在墩顶，由底板、焊接在底板上的三角形钢板以及用螺栓铆在三角形板顶部的半球形传力键组成。钢阻尼器采用三角形钢板为基本构件，在面外水平地震作用下沿高度范围内全截面屈服耗能，具有理想的耗能能力；同时，通过半球形传力键与上顶板钢挡块两侧的聚四氟乙烯板接触连接，能够很好地适应桥梁纵向较大的位移变形，而采用半球形传力键作为传力点，能够适应主梁横向复杂的变形，保证金属阻尼器在地震作用下传力路径明确。地震时，上部结构惯性力通过钢挡板和半球形传力键可靠地传递到三角形板的顶点，使三角形板发生屈服耗能；地震后，可以方便地仅更换下半部分以恢复钢阻尼器的正常功能。

在横向地震作用下，墩、梁间会发生横向相对位移。当位移较小时，板式橡胶支座发生剪切变形，基本保持弹性，直到支座剪力超过支座顶的摩擦力，则支座发生滑动，通过摩擦耗能，其力学特性可采用理想双线性模型，如图 2(a) 所示，主要模型参数为支座摩擦力 F_y、剪切刚度 K_y、支座滑动时变形 d_v。而钢阻尼器¹¹的力学特性可采用双线性模型模拟，如图 2(b) 所示，主要模型参数为阻尼器屈服力 F_{\text{eff}}、K_y、屈后刚度 K_h、极限位移能力 D_u，钢板屈服后的硬化可以控制震后的残余变形。

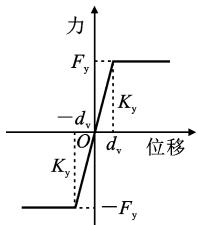
(a) 板式橡胶支座

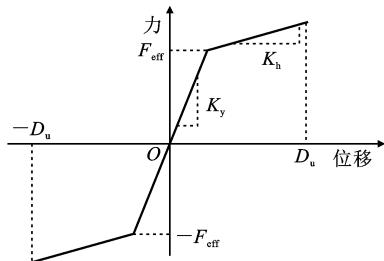
(b) 钢阻尼器

图 2 钢阻尼器体系力学特性

1.1.2 钢挡块体系

钢挡块体系由板式橡胶支座和横向钢挡块组成，如图 3 所示。

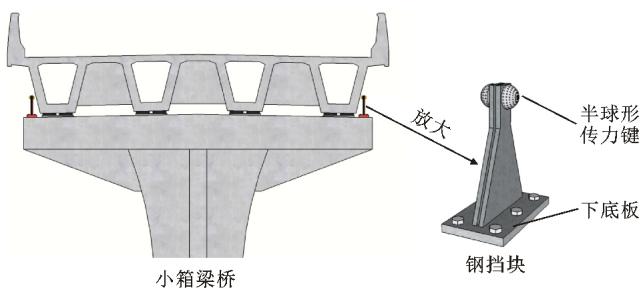
图 3 钢挡块体系示意

其中，板式橡胶支座采用常规方法设置在小箱梁底，承担桥梁竖向荷载，地震时允许滑动并通过摩擦耗能。钢挡块设置在桥墩顶盖梁处、主梁外侧（两侧对称设置），其构造是在前述钢阻尼器的基础上改进而成，由底板、焊接在底板上的 2 片三角形钢板以及用螺栓铆在 2 片三角形板顶部的半球形传力键组成，继承了阻尼器传力可靠、位移能力优越的优点。地震时，如果墩梁相对位移超过挡块间隙，则主梁惯性力通过半球形传力键可靠地传递到三角形板的顶点，使三角形板发生屈服耗能，控制墩梁相对位移；地震后，可以方便地更换钢挡块。

当桥梁设置横向挡块时，由于碰撞效应，挡块间隙对桥梁横向地震反应影响显著，其具体取值一直是个难题。在钢挡块体系中，建议挡块间隙取板式橡胶支座发生滑动时的位移 d_v，这样既可以充分发挥支座的柔性减震作用，减小碰撞效应，又不会出现随遇平衡的振动状态。一般情况下，支座滑动时的剪切位移 d_v 会小于支座允许剪切位移，因此挡块体系也可以保护支座，使支座不会发生剪切破坏。

在横向地震作用下，墩、梁间会发生横向相对位移。当位移较小时，板式橡胶支座发生剪切变形，基本保持弹性，直到支座剪力超过支座顶的摩擦力，则支座发生滑动，通过摩擦耗能，其力学特性可采用理想双线性模型模拟，如图 4(a) 所示，主要模型参数为支座摩擦力 F_y、K_y、支座滑动时变形 d_v。而钢挡块，只有在墩梁相对位移大于挡块间隙时，才发挥作用，其力学特性可采用双线性模型模拟，如图 4(b) 所示，主要模型参数为间隙 \Delta_b、挡块屈服力 F_{\text{eff}}、K_y、屈后刚度 K_h、极限位移能力 D_u，利用钢阻尼器屈服后刚度可控制阻尼器的震后残余变形。

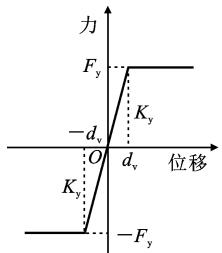
(a) 板式橡胶支座

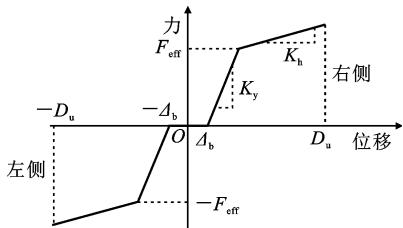
(b) 钢挡块

图 4 钢挡块体系力学特性

1.2 钢阻尼器和钢挡块的拟静力试验

为了验证新型钢挡块和钢阻尼器的构造合理、有充分的位移能力，采用 Q345-E 钢材分别制作了试件 A1 和试件 A2 进行拟静力试验，并将试验结果与有限元数值分析结果进行了对比。选用 Q345 的原因是实际桥梁中需要钢阻尼器提供较高的强度；选用 E 级钢材可以进一步提高三角形钢板的韧性，以增加钢板的位移能力。试件 A1 由 4 片三角形钢板组成，每 2 片紧密地贴合在一起（模拟钢挡块），以验证钢挡块构造的合理性；试件 A2 由 3 片三角形钢板组成（模拟钢阻尼器），以验证钢阻尼器中多块钢板同步受力的情况，具体参数见表 1。

表 1 试件参数

Tab. 1 Parameters of Specimens

编号	三角形钢板数	高 H/\text{m}	宽 B/\text{m}	厚 t/\text{m}
A1	4	0.55	0.6	0.03
A2	3	0.55	0.6	0.03

采用水平液压作动器 (MTS, 50 \text{t}) 进行水平往复循环加载，加载点位于钢阻尼器上挡板侧面。为了保证作动器只发生水平方向运动，将上顶板四周往下伸出 4 块工字钢，工字钢底部采用轴承滚轮，使其在地面上铺设的钢轨上滑动。为防止加载过程中发生向上翘曲，在上顶板上施加 10 \text{t} 恒载压重。试件 A1 和 A2 的加载示意如图 5 所示。

(a) 试件 A1

(b) 试件 A2

图 5 试件加载

图 6 给出试件 A1 和 A2 在循环荷载作用下的滞回曲线和骨架曲线，并与采用 ANSYS 建立的板壳模型进行数值分析得到的结果进行对比。由图 6 可知：试件 A1 和 A2 的滞回面积均较饱满，说明其耗能能力大；有限元模拟滞回曲线与试验吻合度较好，说明 ANSYS 板壳模型能够很好地模拟金属阻尼器的滞回曲线。

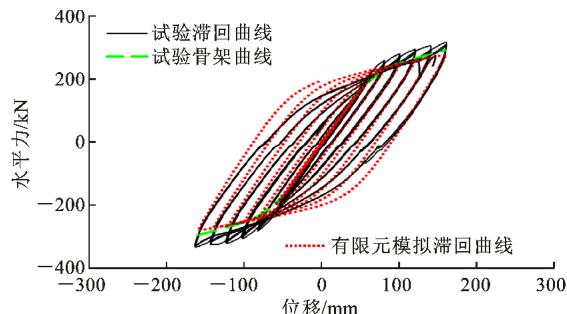
(a) 试件 A1

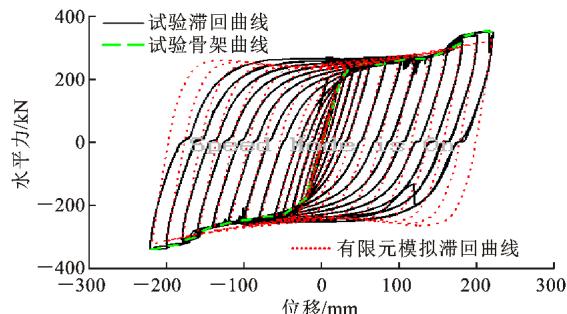
(b) 试件 A2

图 6 滞回曲线和骨架曲线

Fig. 6 Hysteresis Curves and Skeleton Curves

2 组试件接近破坏时的状态如图 7 所示。此时试件 A1 的水平位移加载到 160 \text{mm}，A2 位移加载到 220 \text{mm}。试件 A1 和 A2 均没有发生结构性破坏，只是半球形传力键内的螺栓直径设计较小 (10 \text{mm})，致使在较大水平力时，螺栓发生剪切破坏导致加载结束。通过 ANASYS 数值模拟结果发现：当试件 A1 水平位移达到 160 \text{mm} 时，三角板板底最大应变是材料屈服应变的 30 倍；试件 A2 达到 220 \text{mm} 时，三角板板底最大应变是材料屈服应变的 50 倍。说明选用 Q345-E 型钢材的塑性性能较好，至少能采用 50 倍以上的屈服应变作为破坏应变。

(a) 试件 A1

(b) 试件 A2

图 7 试件加载（接近破坏时）

Fig. 7 Load Configuration of Specimens (near Failure)

由拟静力试验可知：钢阻尼器和钢挡块的构造设计合理，传力路径明确，位移能力较大，均可用等效双线性模型模拟。通过合理地设计连接螺栓的抗剪能力，可充分发挥两者的位移能力。

1.3 减震体系的力学参数确定

在进行钢阻尼器体系和钢挡块体系的构造设计和桥梁的地震反应分析时，需要分别确定板式橡胶支座、钢阻尼器、钢挡块力学模型中的相关参数。

板式橡胶支座力学模型中的各参数分别采用式 (1) \sim (3) 计算

式中：\mu_d 为橡胶与梁底预埋钢板间的动摩阻系数；N 为支座所承担的上部结构恒载；G 为支座的动剪切模量；A 为支座的剪切面积；\sum t 为橡胶片的总厚度。《公路桥梁抗震设计细则》（JTG/T B02-01—2008）和《城市桥梁抗震设计规范》（CJJ 166—2011）均建议 \mu_d 取 0.10，G 取 1200 \text{kN} \cdot \text{m}^{-2}。

由于钢阻尼器和钢挡块的基本耗能构件均为三角形钢板，因此其力学模型取决于钢板的尺寸和力学特性。三角形钢板的尺寸可用底边宽度 B、高度 H，厚度 t 表示，为了得到较均匀的应变分布，B/H 的合理范围为 0.67 \sim 1.50 ¹³。地震力 F 通过半球形传力键作用到三角形钢板的顶点，单块钢板的弹性刚度 K_y、屈服力 F_{\text{eff}} 可采用以下公式计算¹³

而单块钢板的屈后刚度与尺寸的关系复杂，难以用单一公式表达。本文结合小箱梁桥的构造特点，选取厚度 t=2 \text{cm} 的 Q345 钢材（屈服强度 \sigma_y = 345 \text{MPa}，弹性模量 E = 2.05 \times 10^5 \text{MPa}，极限应变 \varepsilon_u 取屈服应变的 50 倍 )，拟定了一组合理尺寸（表 2）。

表 2 各尺寸三角形钢板力学参数

Tab. 2 Mechanical Parameters of Triangular Steel Plates with Different Sizes

高度 H/\text{cm}	宽度 B/\text{cm}	屈服力 F_{\text{eff}}/\text{kN}	弹性刚度 K_y/(\text{kN} \cdot \text{m}^{-1})	硬化率	极限位移 D_u/\text{cm}
25	17.0	20.0	2974	0.067	12.0
	37.5	46.0	6560	0.071	10.0
30	20.0	20.0	2025	0.053	16.0
	45.0	46.0	4555	0.054	13.0
40	27.0	23.9	1153	0.056	17.9
	57.0	44.5	2434	0.079	18.5

针对表 2 中所示尺寸的三角形钢板，采用 ANSYS 程序¹³建立实体有限元模型进行推倒分析，可得到三角形板顶点的力 - 位移曲线，再基于能量等效原则，得到如图 2(b) 所示的双线性模型，具体的力学参数见表 2。从表 2 可知，在这些尺寸范围内，三角形钢板的硬化率（屈后刚度与弹性刚度的比值）均值为 0.063。大量参数分析表明¹⁴，钢阻尼器的 3 个力学参数中，对桥梁地震反应影响较大的是屈服力。因此，在对钢阻尼器（挡块）体系进行结构设计时，可以根据地震反应分析确定钢阻尼器（挡块）的屈服力及最大地震位移，然后选择合适的三角形板的尺寸和块数。对于钢阻尼器的屈服力，建议取值为上部结构恒载反力的 5\% 左右⁶，本例中为 376 \text{kN}，由此确定屈服力变化范围为 0 \sim 800 \text{kN}，可涵盖板数为 1 \sim 20 块，板高在 25 \sim 40 \text{cm} 内，满足合理高宽比的钢阻尼器和钢挡块。

2 两种减震体系的耗能特性分析

减震体系通过减震装置来耗散地震能量以达到减小地震反应的目的，因此，对减震体系的耗能特性进行分析具有重要的意义。为此，以一座典型简支小箱梁桥为例，建立了横向约束体系和 2 种减震体系（钢阻尼器体系和钢挡块体系）共 3 个有限元模型，其中横向约束体系作为对照组用来评价减震体系对墩底内力的影响，选择实际的地震记录作为输入进行非线性时程反应分析，确定合理的钢阻尼器屈服力之后，深入比较钢阻尼器体系和钢挡块体系的减震效果和耗能特性。

2.1 桥梁动力计算模型

在对现有典型简支小箱梁调研的基础上，确定了典型简支小箱梁桥的尺寸、构造。跨径为 30 \text{m}，桥宽 11 \text{m}；桥墩高 8.5 \text{m}，采用 C40 混凝土矩形截面，纵、横向尺寸分别为 1.4 \text{m}, 2.5 \text{m}，墩顶盖梁上设置 2 \times 8 个 GYZ300 普通板式橡胶支座；采用 2 \times 2 桩基础，桩径 1.2 \text{m}，承台尺寸为 5.2 \text{m} \times 5.2 \text{m} \times 2 \text{m}。

基于 OpenSees 软件¹⁵，建立如图 8 所示的单墩有限元模型进行地震反应分析。其中，桥墩采用弹性梁柱单元模拟，盖梁质量为 79.9 \text{t}，承台质量为 135.2 \text{t}，一跨主梁总质量为 673.2 \text{t}；基础采用六弹簧模拟，弹簧刚度采用《公路桥涵地基与基础设计规范》（JTG D63—2007) 中的 M 法计算，纵、横、竖向平动刚度分别为 1.50, 0.50, 7.09 \text{GN} \cdot \text{m}^{-1}，绕纵、横、竖向转动刚度分别为 21.25, 21.25, 3.33 \text{GN} \cdot \text{m}^{-1}。墩顶板式橡胶支座采用如图 2(a) 所示的理想双线性模型模拟，弹性总刚度为 22250 \text{kN} \cdot \text{m}^{-1}，滑动位移为 30 \text{mm}，屈服力为 667.5 \text{kN}。钢阻尼器体系和钢挡块体系在墩顶并联 1 个相应的双线性弹簧，共同传递水平力。钢阻尼器采用 Steel01 材料，可以用来模拟考虑随动硬化的双线性钢材；钢挡块采用考虑损伤的 ElasticPPGap 单元，通过设置 Gap 考虑梁体和挡块的间隙，并通过设置 damage 选项考虑钢板残余变形的影响，即钢板一旦屈服，主梁再次碰上挡块前的间隙将会计入前一次产生的残余变形。

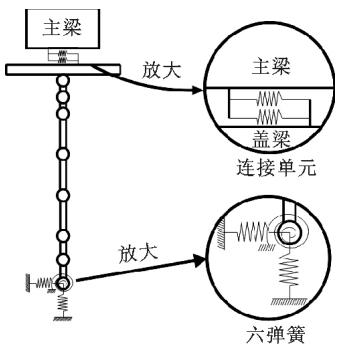
图 8 简化单墩模型

2.2 地震输入

以《城市桥梁抗震设计规范》（CJJ166—2011）的二类场地规范反应谱（特征周期 0.4 \text{s}，地震加速度峰值为 0.4g）为目标，从太平洋地震工程中心（PEER）的强震数据库中筛选了 7 条地震加速度记录（表 3），通过调整各地震记录的加速度值，使 7 条地震记录的平均加速度反应谱与规范反应谱一致，并将调整好峰值的地震动加速度记录作为后续时程分析的地震输入。图 9 将这 7 条地震动加速度记录的对应反应谱与规范反应谱进行了比较，可见，这 7 条地震动加速度记录的平均反应谱与规范反应谱是一致的。

表 3 地震动记录

Tab. 3 Ground Motion Records

编号	地震事件	记录台	PGA 调整系数
1^\#	1971, San Fernando	2516 Via Tejon PV	11.021
2^\#	1971, San Fernando	Isabella Dam (Aux Abut)	51.200
3^\#	1978, Tabas Iran	Boshrooyeh	4.096
4^\#	1979, Imperial Valley	Parachute Test Site	3.542
5^\#	1968, Borrego Mtn	San Onofre-So Cal Edison	9.840
6^\#	1971, San Fernando	LA-Hollywood Stor FF	1.574
7^\#	1976, Friuli Italy	Barcis	21.058

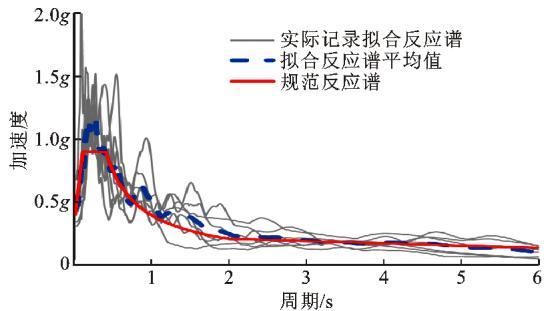
图 9 七条地震动加速度记录的拟合反应谱

Fig.9 Seven Ground Motions Compatible with Response Spectrum

2.3 钢阻尼器(钢挡块)屈服力的确定

为了确定合适的钢阻尼器屈服力，基于前述的动力计算模型和地震输入，以阻尼器减震体系的阻尼器屈服力为变化参数，进行了各体系的横向地震反应分析，结果取 7 条地震记录的平均值。其中，阻尼器的弹性刚度与屈服力之比、硬化率均取表 2 中的平均值，分别为 146.3、0.06。至于挡块体系，考虑到挡块需要对称设置在主梁两侧，因此其屈服力取为阻尼器屈服力的一半。图 10、11 分别给出了最大墩底弯矩、最大墩梁相对位移随阻尼器（挡块）屈服力的变化关系曲线。由图 10、11 可知：减震体系的墩底弯矩对地震输入不敏感，但最大墩梁相对位移受地震输入影响较大。

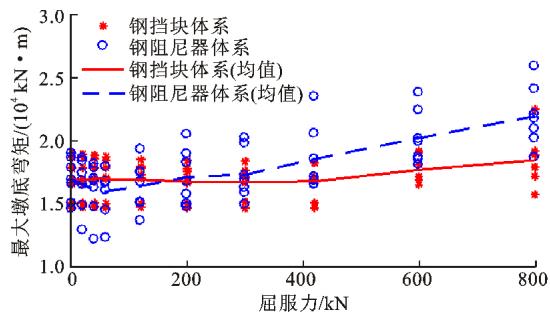
图 10 最大墩底弯矩 - 屈服力关系

Fig. 10 Relationship Between Maximum Pier Bottom Moment and Yield Force

从图 10、11 可见：阻尼器（挡块）屈服力的增大对墩底弯矩影响较小，最大弯矩约为 2.2 \times 10^4 \text{kN} \cdot \text{m}，与墩梁横向固定约束体系的地震弯矩 (4.17 \times 10^4 \text{kN} \cdot \text{m}) 相比，有显著的减震效果；但阻尼器（挡块）屈服力的增大对墩梁相对位移的影响较大，当屈服力小于 400 \text{kN} 时，墩梁相对位移随屈服力的增大而迅速减小，之后减小趋势渐缓。这一现象说明，在一定范围内（屈服力小于 400 \text{kN}），屈服力的增大对下部结构地震内力影响较小，但会显著减小横向地震下最大墩梁相对位移。因此，钢阻尼器（挡块）屈服力的确定主要由墩梁相对位移控制。从经济有效的角度考虑，可选择图 11 中迅速下降段结束时对应的屈服力作为设计值，即阻尼器的屈服力选择 300 \text{kN} 是比较合适的，相当于上部结构恒载反力的 5\% 左右，这也验证了本文第 1.3 节中减震体系参数取值的合理性。

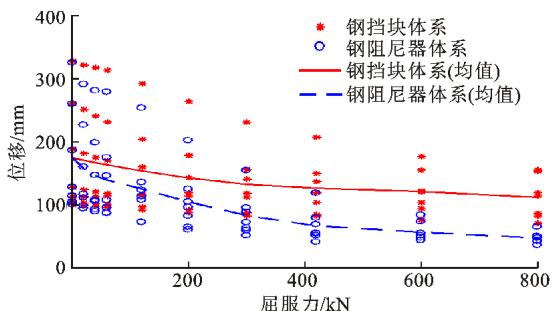
图 11 墩梁相对位移 - 屈服力关系

Fig. 11 Relationship Between Displacement and Yield Force

图 11 还表明，在控制墩梁相对位移方面，阻尼器体系与挡块体系相比具有相当大的优势。主要原因是，挡块体系只有梁体碰上挡块时，挡块才发挥作用，且只有碰上的这一侧挡块起作用；而阻尼器体系只要墩梁间发生相对位移，阻尼器就起作用，因此，减震效率高。此外，钢挡块的位移能力应根据最大墩梁相对位移减去挡块间隙来确定。

2.4 两种体系的耗能特性比较

根据本文第 2.3 节参数分析的结果，屈服力取 300 \text{kN} 时，墩梁相对位移得到了有效控制，且位于曲线迅速下降段结束处，经济可靠。文献⁶建议屈服力为上部结构恒载反力的 5\% 左右（本例中为 376 \text{kN})，验证了本文取值的合理性。基于以上分析，以相同成本为前提，2 种减震装置均选择了相同的板数，因为钢挡块横桥向对称设置，所以屈服力和初始刚度为钢阻尼器的一半，即钢阻尼器屈服力、弹性刚度、硬化率分别为 300 \text{kN}, 29300 \text{kN} \cdot \text{m}^{-1}, 0.06; 钢挡块间隙、屈服力、弹性刚度、硬化率分别为 3 \text{cm}, 150 \text{kN}, 14650 \text{kN} \cdot \text{m}^{-1}, 0.06。将表 3 中 7 条地震记录分别输入，进行 2 种体系桥梁结构的地震反应和耗能特性分析，从中选择了 2 种典型的地震反应结果（对应 1^\# 和 2^\# 地震记录）见图 12。

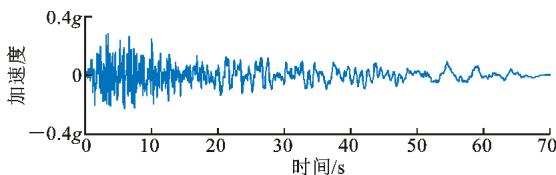
(a) 1^\# 号地震记录

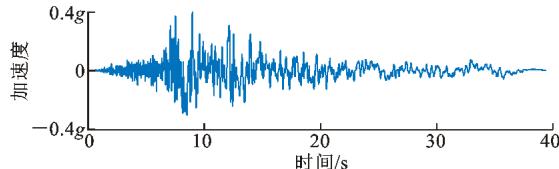
(b) 2^\# 号地震记录

图 12 地震加速度时程

Fig. 12 Seismic Acceleration Time-history

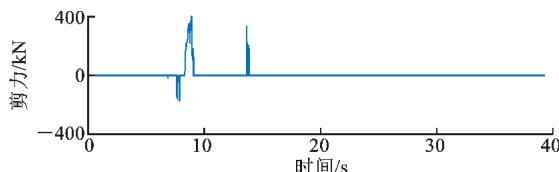
图 13、14 分别给出了 2 条地震记录输入下，2 种减震体系中钢挡块和钢阻尼器的横向剪力时程曲线。由图 13、14 可见：地震产生的挡块剪力随时间呈锯齿状分布，只有被主梁碰上的一侧挡块才发挥作用；阻尼器在正、负方向均可随时提供恢复力，剪力随时间连续变化。另外，当输入地震加速度时程的能量在正、负方向较为均衡时，梁体和挡块碰撞次数较多，两侧挡块都能发挥作用；反之，可能只有一侧挡块发挥作用。

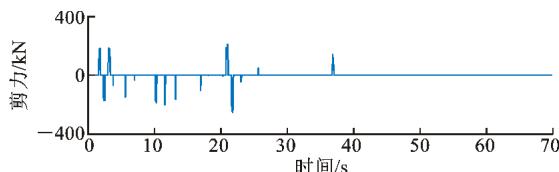
(a) 钢挡块

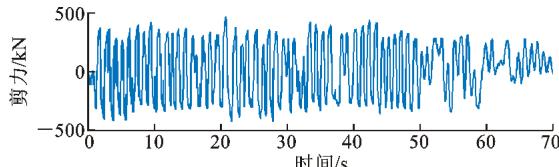
(b) 钢阻尼器

图 13 钢阻尼器 (挡块) 横向地震剪力时程 (1^\# 号地震记录）

Fig. 13 Time-history of Transverse Seismic Shear of Steel Damper (or Block) (No. 1 Earthquake Record)

(a) 钢挡块

(b) 钢阻尼器

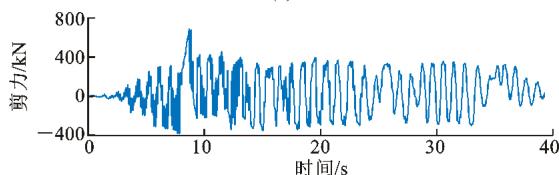
图 14 钢阻尼器 (挡块) 横向地震剪力时程 (2^\# 号地震记录）

Fig. 14 Time-history of Transverse Seismic Shear of Steel Damper (or Block) (No. 2 Earthquake Record)

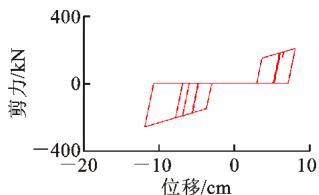
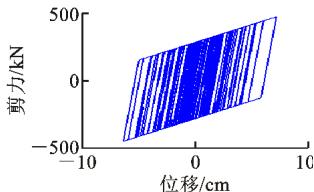
图 15、16 分别给出了 2 条地震记录输入下，2 种减震体系中钢挡块和钢阻尼器的滞回曲线。由图 15、16 可知：对于 2 条地震记录，钢阻尼器的滞回曲线均较为饱满，耗能能力较大，而钢挡块的滞回圈数较少，耗能能力较差。当地震加速度时程的正、负方向能量分布不均衡时 (2^\# 地震记录 )，挡块的滞回圈数会显著减少，原因是：当一侧挡块发生较大塑性变形后，墩梁相对位移只有再次超过挡块间隙和残余变形之和时，挡块才能再次提供恢复力，导致另一侧挡块不能发挥作用，耗能能力可以忽略。

(a) 钢挡块

(b) 钢阻尼器

图 15 钢阻尼器 (挡块) 滞回曲线 (1^\# 号地震记录）

Fig. 15 Hysteresis Curve of Steel Damper (or Block) (No. 1 Earthquake Record)

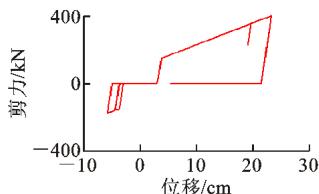
(a) 钢挡块

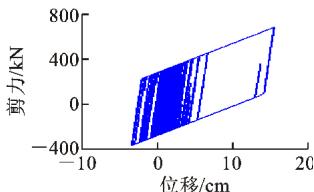
(b) 钢阻尼器

图 16 钢阻尼器 (挡块) 滞回曲线 (2^\# 号地震记录）

Fig. 16 Hysteresis Curve of Steel Damper (or Block) (No. 2 Earthquake Record)

图 17 给出了 2 条地震记录输入下，2 种减震体系墩底的弯矩时程，并标注了不同减震体系的弯矩最大值。由图 17 可知，2 种体系的墩底弯矩相差不大（10\% 以内）。由于同一时刻只有一侧钢挡块传力，因此钢挡块体系的墩底弯矩相对较小。

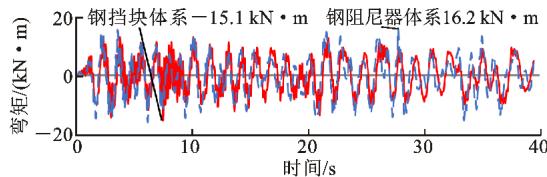
(a) 1^\# 号地震记录

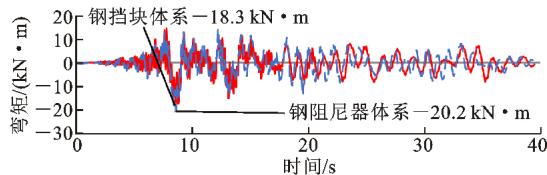
(b) 2^\# 号地震记录

图 17 钢阻尼器 (挡块) 体系横向墩底弯矩时程

Fig. 17 Time-history of Pier Bottom Moment of Steel Damper (or Block) System

为了进一步分析钢阻尼器体系和钢挡块体系的耗能特性，对 2^\# 号地震记录对应的支座和阻尼器（挡块）的滞回曲线进行积分，得到 2 种体系中支座、阻尼器（挡块）的耗能时程，如图 18 所示。表 4 则进一步对 2 种体系的支座、钢阻尼器（挡块）的耗能进行了定量比较。从图 18 和表 4 可知，在钢阻尼器体系中，钢阻尼器和支座共同耗能，且阻尼器耗散的能量显著大于支座；而在钢挡块体系中，主要由支座耗散能量，挡块的耗能作用有限，特别是当地震加速度时程的正、负方向能量不均衡时，挡块的耗能作用可以忽略。另外，在同样的地震输入下，钢挡块体系中的支座耗能是钢阻尼器体系中支座的 2 \sim 3 倍，因此，钢挡块体系中的支座较易遭受地震损伤。

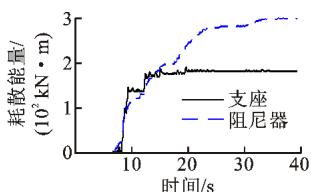
(a) 钢阻尼器体系

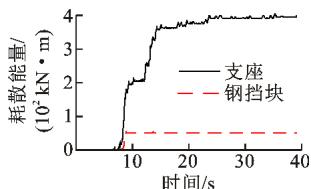
(b) 钢挡块体系

图 18 减震体系的耗能时程曲线

Fig. 18 Energy Dissipation Time-history Curves of Seismic Systems

表 4 不同地震动输入下 2 种体系耗能比较

Tab. 4 Comparison Between Energy Dissipation of Two Systems Under Different Ground Motion Inputs 10^2 \text{kJ}

地震输入编号	钢挡块体系	钢阻尼器体系
	支座	钢挡块
1^\#	10.30	0.22
2^\#	4.06	0.56

总体而言，考虑到经济性和安装便利性，在中低烈度区，地震位移较小，推荐使用钢挡块体系；而在高烈度区，地震位移较大，推荐使用钢阻尼器体系。

3 结语

（1）以三角形钢板为基本耗能构件，提出的板式橡胶支座和钢阻尼器组合、板式橡胶支座和钢挡块组合的减震体系，构造简单、力学性能明确，与横向约束体系相比，能够显著减小桥梁下部结构地震内力，并且能充分发挥支座的摩擦耗能作用。

（2）减震体系的关键设计参数是钢阻尼器（挡块）屈服力，在一定范围内，屈服力的增大对下部结构地震内力影响较小，但会显著减小横向地震下最大墩梁相对位移。从经济有效的角度考虑，减震装置的屈服力应选择在合适的范围内。

（3）地震作用下，钢阻尼器的耗能大，通过耗能及恢复力能有效控制墩梁相对位移，而钢挡块耗能小，特别是地震动在正、负方向能量分布不均衡时，主要通过为梁体提供恢复力来控制墩梁相对位移，因此钢阻尼器体系的限位效果要优于挡块体系。钢挡块体系适用于地震位移较小的低烈度区；钢阻尼器体系适用于地震位移较大的高烈度区。

（4）下一步需要针对 2 种减震装置进行构造设计和三角形板的尺寸优化，以充分发挥其减震耗能能力和限位作用。

---

参考文献

References: