桥梁高桩承台群桩基础在受到地震荷载作用后会在结构体系内产生一定的内力和变形，即地震反应需求。当此需求值小于群桩基础的能力值时，基础结构损伤小，否则，基础结构可能有很大损伤。群桩基础的抗震能力值与桩体、桩周土体和桩土之间的接触等因素有关，何种因素对其抗震能力值贡献大，目前尚不十分明确。要探寻影响群桩基础抗震能力值的因素，就要找到对群桩基础的抗震能力值影响最大的参数，即进行灵敏性分析，得到灵敏性最大的元件。相关学者对桩基础结构进行了参数灵敏性研究，并得出了相应的结论。Hafez 等¹使用联合系统方法，对位于非均匀土层中的桩顶固结群桩结构进行了参数灵敏性分析，得到了灵敏性因子和灵敏性算子，但该法较烦琐，不便于实际应用。De Cock²对单桩的荷载位移特征行为进行了研究，分析影响桩体变形的灵敏性因素，但其研究对象是单桩结构。Xiao XC 等³使用非线性文克勒地基梁模型，对群桩结构进行了动力反应及灵敏性分析，可知桩土刚度比是最重要的灵敏性控制参数，但主要针对群桩结构的地震反应需求，而不是抗震能力。本研究在 OpenSees 平台下，对实际桥梁高桩承台群桩基础建立了有限元模型，考虑非线性因素，采用简便的二阶中心差分法对其进行了抗震能力值的灵敏性分析，得到了影响高桩承台群桩基础抗震能力值的灵敏性参数。

1 分析方法

在有限元分析中连续结构系统被离散化，并表示成一组代数方程为（以静力系统为例）

其中，\tau 为时间变量，h 为系统设计参数；K(\tau, h) 为 N \times N 阶刚度矩阵；Q(\tau, h) 为 N \times 1 阶外节点荷载矩阵，设其显式依赖于 h；q(\tau, h) 为 N \times 1 阶节点位移矩阵，其隐式依赖于 h。传统的力学分析假设设计参数 h 是不变的，结构灵敏性分析则认为系统的反应特性是 h 的函数，显然这是符合实际的，因为现实的结构系统跟理想结构有差别，如结构几何和材料缺陷等。

结构响应灵敏性是指结构设计参数 h 发生单位变化量时，结构响应产生的变化数量。响应灵敏性 \psi = \Delta q / \Delta h 的计算方法主要有有限差分法 FDM（finite difference method）、直接微分法 DDM（direct differentiation method）、联合系统方法 ASM（adjoint system method）和半解析方法（semi-analytical method）⁴。其中，FDM 与 DDM 操作简便，较为常用，其余方法都较为烦琐，实际应用较困难。虽然 DDM 在效率和精度上高于 FDM，但对于非线性结构系统来说，DDM 的算法设计较为困难，FDM 有一定优势，尤其是采用二阶中心差分法后，截断误差在一定程度上得到控制，当然截断误差还和差分步长 \Delta h 的选择有关，其定义式为

本研究采用二阶中心差分法，以若干结构系统参数为随机变量进行摄动，对桥梁群桩基础进行了抗震能力值的灵敏性分析，差分步长 \Delta h 的选择考虑了随机变量的均值与变异系数。

对于桥梁群桩基础的抗震能力值，本研究采用弹塑性静力分析方法，通过对结构或构件施加某一模式的侧向分布力，并逐渐增加，直至结构达到预定的变形状态或倒塌状态，得到极限地震作用下结构的抗震能力和行为特征。

进行弹塑性静力分析时，侧向力加载模式对计算结果影响很大，其主要与结构产生的惯性荷载密切相关⁵,⁶。在地震作用下，群桩基础与土体的动力相互作用包括运动学效应和动力学效应，可忽略桩周土产生的运动学效应，仅考虑动力学效应，此时惯性力由基础以上结构传下来的地震惯性力、承台的地震惯性力以及桩身的地震惯性力等 3 部分组成。桥梁地震反应需求分析表明，前两部分的贡献起控制作用，第 3 部分的贡献所占比重较小，可忽略。上部结构传至承台底的地震惯性力可视为集中力，包括轴力、剪力和弯矩。因此，对群桩基础进行弹塑性静力分析时，侧向加载模式可采用在承台中心施加侧向集中力的模式，承台所受的轴力和弯矩可由施加在承台中心的轴力和弯矩替代。桥梁群桩基础的抗震能力的衡量指标为位移、抗力和延性。对于灵敏性而言，延性可由响应位移间接得到，故本研究只对位移和抗力进行灵敏性研究。

2 群桩基础有限元模型

2.1 有限元模型概述

本研究在 OpenSees 平台⁷中建立了群桩基础有限元模型，如图 1。模型中桩体采用弹塑性纤维梁柱单元模拟，每根单桩桩底固结，桩顶节点之间采用刚臂连接，承台重量及上部结构反力通过在承台形心处（图 1 中 A 点）施加集中力来代替，桩周土体采用非线性 p-y 弹簧单元模拟。

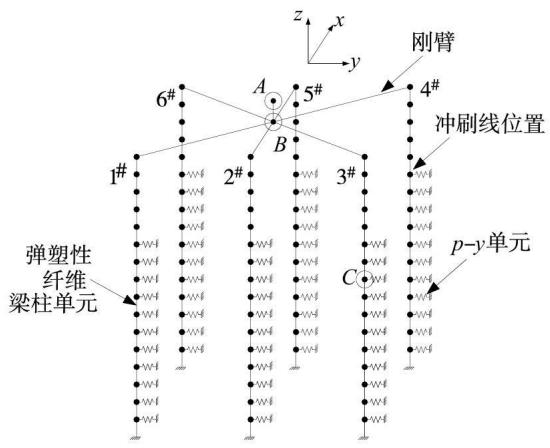
图 1 三维有限元模型

Fig.1 Finite element model

2.2 桩体单元

桩体采用弹塑性纤维梁柱单元⁸模拟，该单元是一种非线性分布塑性单元，单元沿轴向被离散成许多段，每一段的特性由中间横截面代表，而该横截面又进一步被离散成许多纤维（如用矩形网格划分）；每一根纤维可以是混凝土的，也可以是钢筋的，如图 2。计算时首先基于钢筋、混凝土纤维各自的应力 - 应变关系求得各截面的弯曲刚度，然后沿单元长度积分最终得到单元刚度矩阵。

在 OpenSees 平台中，选用 dispBeamColumn 弹塑性梁柱单元模拟桩体，同时用 Fiber 定义纤维截面，并将其组合到 dispBeamColumn 单元中，从而构成弹塑性纤维梁柱单元。

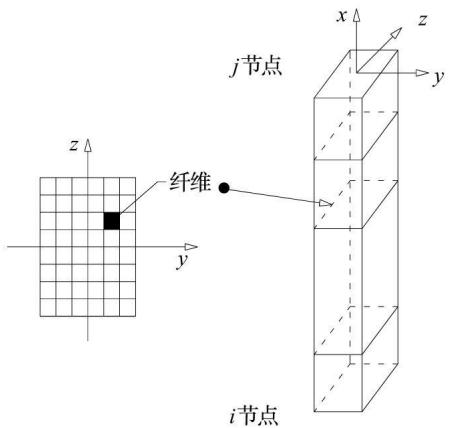
图 2 纤维梁柱单元

Fig.2 Fiber beam column element

2.3 桩体材料本构模型

桩体采用 Kent-Scott-Park 模型⁹作为约束和非约束混凝土本构模型，不考虑混凝土受拉，在 OpenSees 平台中，该模型为 Uniaxial Concrete01 材料。典型的约束混凝土的单调本构曲线如图 3(a)。同时，桩体采用 Giuffre-Menegotto-Pinto 模型¹⁰作为钢筋的本构模型，此模型应用较广泛，与试验数据接近，应变硬化率取 0.001。在 OpenSees 平台中，该模型为 uniaxial Steel02 材料，其典型的单调本构曲线如图 3(b)。

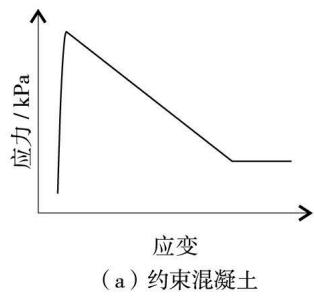
(a) 混凝土

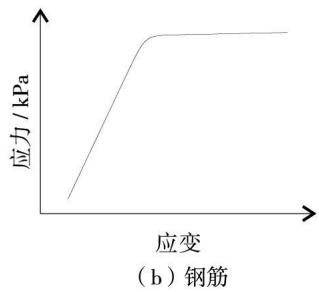
(b) 钢筋

图 3 材料本构曲线

Fig.3 Material constitutive curve

2.4 桩土接触非线性

杆件层次常采用非线性 p-y 单元模拟桩土侧向相互作用、t-z 单元模拟桩侧土摩擦作用和 q-z 单元模拟桩尖土体的支承作用。本研究主要研究群桩基础的侧向抗震能力，分析中仅使用非线性 p-y 单元¹¹。非线性 p-y 单元在 OpenSees 中由 zero-Length 单元组合 PySimple 材料而成，单元两端节点坐标相同，单元一端连接桩身，另一端固定。

本研究对象是软黏土，其土性参数采用 Matlock 的推荐公式¹²。在 OpenSees 平台中，黏土的土性参数变量为 P_{\text{ult}}、y_{50} 和 C_d。其中，P_{\text{ult}} 是 p-y 材料的极限能力值（土体黏聚力的表征），y_{50} 是在单调加载下 P_{\text{ult}} 达到极限值 50\% 时的侧向位移，C_d 为桩土之间间隙完全张开时的桩土之间抗力。

Mokwa¹³研究发现，在平行加载方向上，桩中心距小于 6D (直径)，或者在垂直加载方向上，桩中心距小于 3D 时，群桩效应不可以忽略。考虑群桩效应的简化方法是在单桩的 p-y 曲线上乘以一个被称为 p 乘子的系数，采用该方法考虑群桩效应，p 乘子的数值取自文献¹³。

3 实例分析

3.1 实例描述

实例为上海某长江大桥引桥 PM109 号墩群桩基础，该桩基位于 7 \times 60 \text{m} 的一联连续梁内。该桥分上下两幅，选取其中一幅桥墩桩基。桩基直径为 1.8 \text{m}，桩长为 61.8 \text{m}，冲刷线以上自由长度为 10 \text{m}。冲刷线以下埋置长度为 51.8 \text{m}。桩基纵横向布置成 2 \times 3 的矩形，桩基纵横向中心间距均为 4.65 \text{m}。承台纵横向平面尺寸为 7.65 \text{m} \times 15.2 \text{m}，厚度为 2.8 \text{m}。桩身采用 C30 混凝土，桩身纵筋为 \Phi 35 \text{mm} \times 32 \text{mm}，箍筋为 \Phi 12 \text{mm} \times 150 \text{mm}。保护层为 50 \text{mm}。基础处于单一均匀的黏土层中，黏土不排水剪切强度为 50 \text{kN/m}^2，有效容重为 10 \text{kN/m}^3。

3.2 实例有限元模型

实例群桩基础的有限元模型如图 1 所示，部分桩体单元没有绘出。桩体单元长度均为 2 \text{m}。截面纤维划分如下：对于核心约束混凝土，沿桩基周长方向划为 50 个纤维，沿半径方向划分为 8 个纤维，纤维数为 400 个；对于保护层混凝土，沿桩基周长方向同约束混凝土，沿半径方向划分为 1 个纤维，纤维数为 50 个；对于纵向钢筋，每根钢筋划为一个单元。

混凝土材料中对于约束混凝土，最大抗压强度为 16.73 \text{MPa}，对应最大抗压强度的应变为 0.0025，混凝土极限应变为 0.016，对应极限应变的压溃强度为 8.365 \text{MPa}。对于保护层混凝土，最大抗压强度为 13.8 \text{MPa}，对应最大抗压强度的应变为 0.002，混凝土极限应变为 0.006，对应极限应变的混凝土压溃强度为 0。钢筋材料屈服强度为 280 \text{MPa}，弹性模量为 2.0 \text{E}5 \text{MPa}，屈服后硬化比为 0.001。1 至 6 桩的 p 乘子分别为 0.82, 0.78, 0.82, 0.64, 0.68 和 0.64。每根桩不同深度的 p-y 弹簧参数的计算参见文献¹³。

3.3 加载工况

分析时采用水平单调拟静力加载，加载位置在承台形心处（图 1 中 A 点），加载沿 x 方向，加载由位移控制，最大控制位移为 2 \text{m}。

非线性有限元方程用 Newton-Raphson 法求解，收敛准则为能量准则；由于材料本构关系中存在拐点，加载采用位移控制，可以不使用弧长法而使计算收敛；其他求解设置与 OpenSees 中的常规静力分析相同⁷。

3.4 灵敏性分析参数设置

灵敏性分析时选择了桩体钢筋抗拉屈服强度 f_s、桩体混凝土抗压屈服强度 f_c、桩体核心混凝土截面积 A 以及 p-y 参量 P_{\text{ult}} 作为灵敏性控制参数；因混凝土的弹性模量与其抗压强度有一定的关联，故其弹性模量不作为控制参数。另外，当桩的长度超过一定值后对桩的侧向反应影响很小，故桩长也不作为控制参数。初始分析时，差分步长 \Delta h 取 10^{-2} \mu；对比分析时，\Delta h 分别取 10^{-2} \mu, 10^{-3} \mu 和 10^{-4} \mu，\mu 为控制参数的均值。

3.5 实例分析结果

对于群桩基础的抗震能力而言，灵敏性分析感兴趣的部位是：① 承台底面中心处（图 1 中点 B）；② 冲刷线下 8 \text{m} 左右的桩体处（图 1 中点 C），计算得知在该处桩体的弯矩较大。灵敏性分析感兴趣的内容是上述部位的位移与水平抗力，在单调拟静力加载下，相对于控制参数的灵敏性指标。

单调拟静力加载下反应灵敏性研究对象为点 B 的水平位移 U_B、水平抗力 F_B 以及点 C 的水平位移 U_C，控制参数 h 为 f_s、f_c、A 和 P_{\text{ult}}。本研究对灵敏性分析结果进行归一化为 h q^{-1} \frac{dq}{dh}，其值表示灵敏性控制参数的单位百分变化量产生的结构反应变化百分率¹⁴。

图 4 \sim 图 6 分别为灵敏性研究对象对控制参数的归一化反应灵敏性指数，该指数在图中是加载控制位移的函数。图 4 中，U_B 对参数 A 的灵敏性变化较剧烈，变化范围为 -0.63 \sim 0.14，但随着位移荷载增加，U_B 对参数 P_{\text{ult}} 的灵敏性开始增大，最终达到 0.16，超过参数 A。图 5 中，F_B 对参数 f_s 的灵敏性在位移加载初期为 0，到某一位移量时才开始变化，并逐渐增大，在钢筋屈服前，f_s 对反应基本无影响；对参数 A 的灵敏性数值开始较大，然后逐渐平稳，反映了施工误差对反应的影响；对其余 2 个参数的灵敏性相对较小。图 6 中，U_C 对参数 f_s 和 A 的灵敏性与 F_B 相似；对参数 P_{\text{ult}} 的灵敏性，随着位移荷载的增大一直增加，最大值与参数 f_s 接近。灵敏性研究对象对参数 f_c 的灵敏性相对来说都比较小。从图中数值看，对参数 f_c 的反应灵敏性最小，比其他 3 个参数低 1 个数量级；U_C 对 3 个参数的反应灵敏性较为显著；图中的锯齿状起伏是由于复杂的结构行为导致结构中的内力与变形的重分布而形成。对参数 f_c 的反应灵敏性随着位移荷载的增加基本上逐渐减小，这与预期相符，因为混凝土屈服后进入软化阶段。对参数 f_s 的反应灵敏性随着位移荷载的增加，基本上逐渐增大，因为钢筋屈服后将一直处于强化阶段；同样的现象参数 P_{\text{ult}} 也有。对参数 A 的反应灵敏性随着位移荷载的增加，基本上趋于平稳，只是代表结构施工误差对反应的影响。

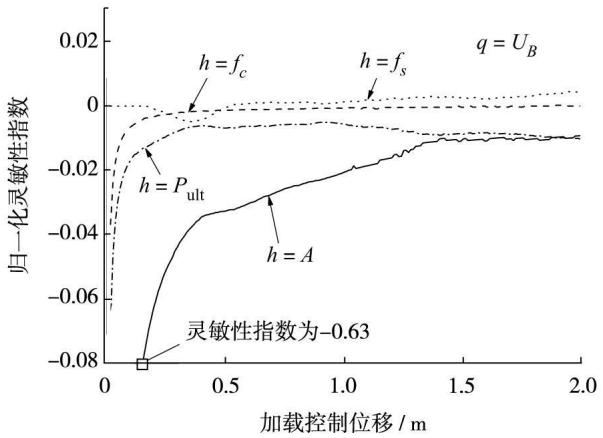
图 4 U_B 的反应灵敏性

Fig.4 Response sensitivity of U_B

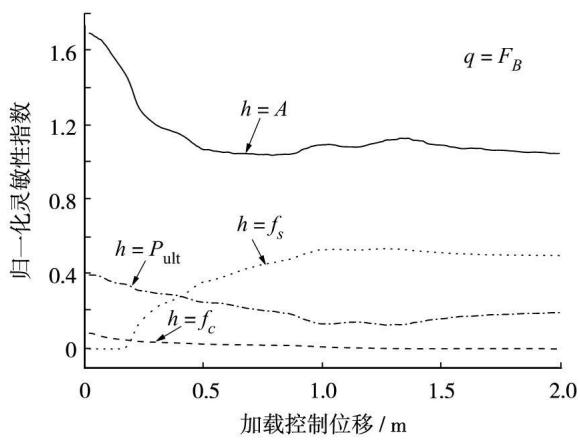
图 5 F_B 的反应灵敏性

Fig.5 Response sensitivity of F_B

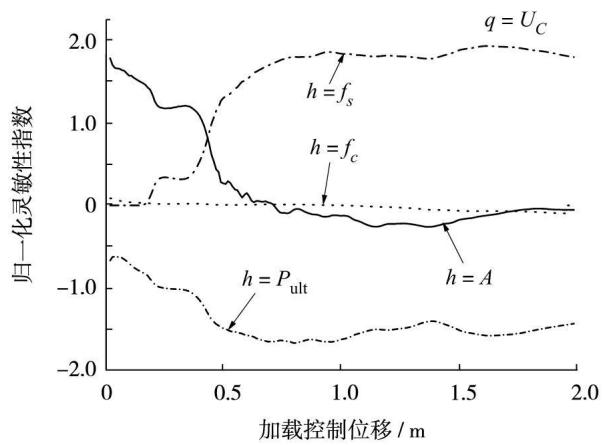
图 6 U_C 的反应灵敏性

Fig.6 Response sensitivity of U_C

为检查差分步长对反应灵敏性计算结果的影响，取 U_C 对 f_s, P_{\text{ult}} 和 A 的反应灵敏性作为研究重点，图 6 中 3 个参数对反应灵敏性起了相对重要作用。图 7 \sim 图 9 为考虑差分步长后，U_C 对 f_s, P_{\text{ult}} 和 A 的反应灵敏性数值变化图，\Delta h 分别取 10^{-2} \mu, 10^{-3} \mu 和 10^{-4} \mu。可以看出，仅在位移加载值较大时，3 种情形下灵敏性值略有差别，U_C 对 P_{\text{ult}} 的反应灵敏性偏差最大，达 6\% 左右，U_C 对 A 的反应灵敏性偏差最小，几乎为 0。

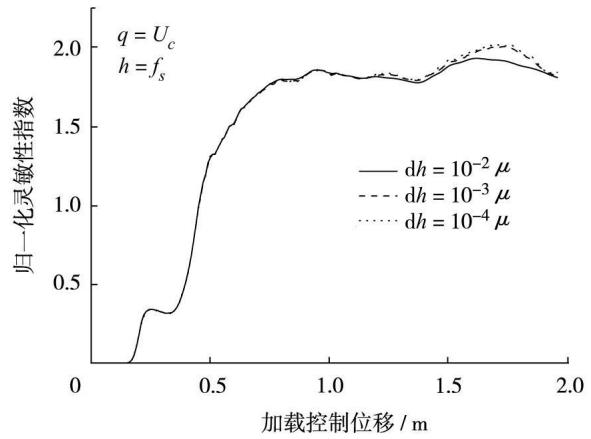
图 7 差分步长对反应灵敏性的影响（U_C 对 f_s）

Fig.7 Influence on response sensitivity (U_C to f_s)

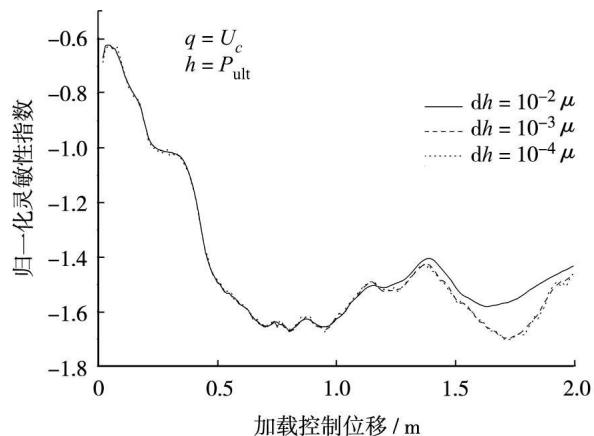
图 8 差分步长对反应灵敏性的影响（U_C 对 P_{\text{ult}}）

Fig.8 Influence on response sensitivity (U_C to P_{\text{ult}})

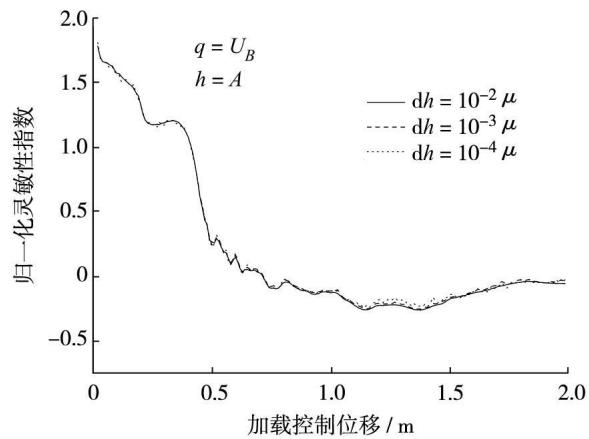
图 9 差分步长对反应灵敏性的影响（U_C 对 A）

Fig.9 Influence on response sensitivity (U_C to A)

4 结语

综上分析可知：① 高桩承台群桩基础的抗震能力值各衡量指标（水平位移与抗力）对结构控制参数的反应灵敏性，总体上对混凝土抗压屈服强度的反应灵敏性较小，对钢筋抗拉屈服强度和土体黏聚力的反应灵敏性较大，对桩体核心混凝土截面积的反应灵敏性较平稳。② 高桩承台群桩基础承台底部中心处的水平位移对土体黏聚力和桩体核心混凝土截面积的反应灵敏性较显著，但数值并不大。③ 高桩承台群桩基础承台底部中心处的水平抗力对钢筋抗拉屈服强度和桩体核心混凝土截面积的反应灵敏性较大，数值高出承台底部中心处水平位移的反应灵敏性一个数量级。④ 冲刷线下 8 \text{m} 左右的桩体处的水平位移对钢筋抗拉屈服强度和土体黏聚力的反应灵敏性较大，数值也高出承台底部中心处水平位移的反应灵敏性一个数量级。⑤ 在大位移荷载下，差分步长对反应灵敏性计算结果的影响，最大达到 6\% 左右；差分步长取 10^{-2} 倍均值是合理的。⑥ 进一步的高桩承台群桩基础动力可靠度分析要重点考虑钢筋抗拉屈服强度与土体黏聚力对系统失效概率的影响。

参考文献