PDF BibTeX

---

0 引言

自 21 世纪以来，中国斜拉桥的建设成就举世瞩目。由于斜拉桥在交通网络中的重要性以及震后桥塔及基础损伤修复的困难性，目前，中国抗震设计规范要求斜拉桥主塔及基础在设防地震下保持弹性¹,²。对于纵桥向，斜拉桥常采用漂浮或半漂浮体系，且可以采用液压黏滞阻尼器限制主梁位移，因此其纵向抗震性能通常较好³,⁴。而在横桥向，墩梁、塔梁间常采用刚性连接以满足抗风和正常使用荷载要求，导致主塔、边墩及其基础地震力较大，往往控制着斜拉桥的设计，通常需要增大截面配筋来满足抗震设防要求。从这点上讲，传统的“硬抗”并不是经济的设计策略。近年来，如何改善和提高斜拉桥横向抗震性能引起了国内外学者的关注。

随着被动控制技术的发展，不少学者开发和应用减震耗能装置以改善斜拉桥的横向抗震性能，并采用数值方法验证其有效性。叶爱君等⁵,⁶将液压黏滞阻尼器放置于墩梁连接处，显著改善了桥墩及其基础的抗震性能；希腊 Rion-antirion 桥塔梁间横向采用液压黏滞阻尼器和“熔断”约束装置来适应强震作用及断层位移⁷；Ismail 等⁸提出了一种适用于近场地震的减震装置；Guan 等⁹提出了斜拉桥横向弹塑性索和黏滞阻尼器组成的横向减震系统；沈星等¹⁰开发了能适应桥梁纵向位移的新型横向钢阻尼器（其以三角形钢板为耗能元件），提出了斜拉桥边墩横向减震体系，并研究了阻尼器屈服力对墩梁相对位移、墩底剪力和弯矩的影响¹¹,¹¹。

相对于数值方法，振动台试验是研究和验证桥梁抗震性能更直接和有效的方式。目前，开展的斜拉桥振动台试验主要研究行波效应对斜拉桥地震响应的影响¹³,¹⁴,¹⁵以及斜拉桥的破坏机理¹⁶,¹⁷。近几年，也有部分学者采用振动台试验研究斜拉桥横向减震体系的抗震性能。如 Xu 等¹⁸采用试验验证了 C 形钢阻尼器对中等跨度斜拉桥的横向减震效果；易江等¹⁹采用试验验证了 X 形钢阻尼器对独塔斜拉桥的横向减震效果。需要说明的是，为确保减震体系桥梁的可靠性及有效性，除采用拟静力试验明确减震耗能装置的力学本构外，仍需采用振动台试验检验其能否适应复杂的地震荷载传力路径以及验证其减震效果。

为此，本文以苏通大桥为背景，以桥梁新型横向钢阻尼器¹⁰为减震耗能装置，于同济大学多功能振动台实验室开展了 1/35 的斜拉桥横向减震体系全桥试验。试验中，将钢阻尼器布置于桥墩和桥塔处形成横向减震体系，选取近、远场地震动为输入，并与传统的横向固定体系对比，研究大跨度斜拉桥横向减震体系的行为，并验证其减震效果。

1 试验模型设计

1.1 工程背景

本文以苏通大桥为背景，该桥为双塔双索面斜拉桥，跨径布置为 2 \times 100 \text{m} + 300 \text{m} + 1088 \text{m} + 300 \text{m} + 2 \times 100 \text{m}，总长 2088 \text{m}。其中，桥塔为倒 Y 形混凝土桥塔，总高 297.7 \text{m}，桥塔混凝土为 C50；边跨 3 个桥墩均采用分离的薄壁箱型空心墩，墩身材料为 C40；主梁采用扁平钢箱梁，梁高 4 \text{m}，梁宽 41 \text{m}；斜拉索采用 272 对 1770 \text{MPa} 平行钢丝索；基础为群桩基础。纵向为漂浮体系，塔梁间设有液压黏滞阻尼器；横向采用常规的固定约束体系，即墩、梁间设置横向固定支座，而塔、梁间设有横向抗风支座²⁰。

1.2 结构设计

根据实验室空间和振动台的承载能力，采用 1/35 的几何缩尺比；为保证试验模型的施工质量，采用微粒混凝土代替原型桥的普通混凝土，混凝土弹性模量相似比为 0.3；由于在同一重力场下，加速度相似比为 1；其余相似常数如表 1 所示。由于试验目的是探究和验证横向钢阻尼器的减震效果，而非研究原型桥的抗震性能，出于试验可行性考虑，在保证全桥前 3 阶动力特性相似的基础上，试验模型设计时进行如下简化：忽略基础的影响，将桥墩和桥塔固定在振动台上；将 272 对斜拉索缩减到 56 对，斜拉索采用 7.7 \text{mm} 的钢丝绳代替；由于振动台数量的限制，试验模型去除了近塔辅助墩；为便于桥墩处安装钢阻尼器，原有的分离式桥墩变为带系梁的双柱墩。试验模型布置如图 1 所示。根据桥墩和桥塔截面抗弯和抗剪能力相似，设计了墩身和塔身截面，截面尺寸和配筋如图 2 所示。其中，纵筋采用市场上最小直径的 \Phi 6 \text{HRB400} 钢筋代替，箍筋采用铁丝代替。根据质量相似比，设计了主梁、桥墩和桥塔配重，配重结果如表 2 所示，配重位置见图 1、2。振动台试验模型概况如图 3 所示。

表 1 试验模型相似常数

Table 1 Similarity Constants for Test Model

物理量	相似比	物理量	相似比	物理量	相似比
长度 l	1/35	应变 \varepsilon	1.000	质量 m	0.000240
加速度 a	1.0	密度 \rho	10.500	力 F	0.000240
弹模 E	0.3	时间 t	0.169	弯矩 M	0.000007

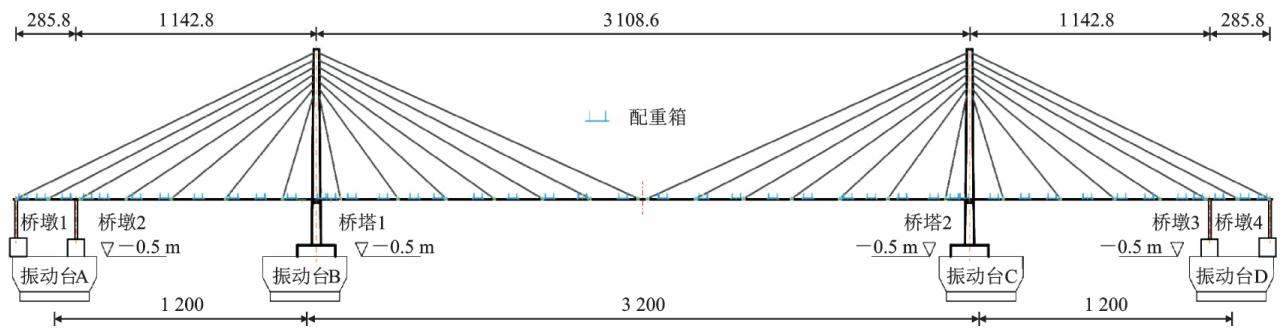
图 1 试验模型布置（单位：\text{cm}）

Fig.1 Layout of Test Model (Unit: \text{cm})

表 2 结构配重

Table 2 Additional Mass of Structure \text{kg}

构件	自质量	附加质量	总质量
主梁	2970	12889	15859
桥塔 1, 2	2131	13876	32014
桥墩 1, 2, 3, 4	210	916	4504

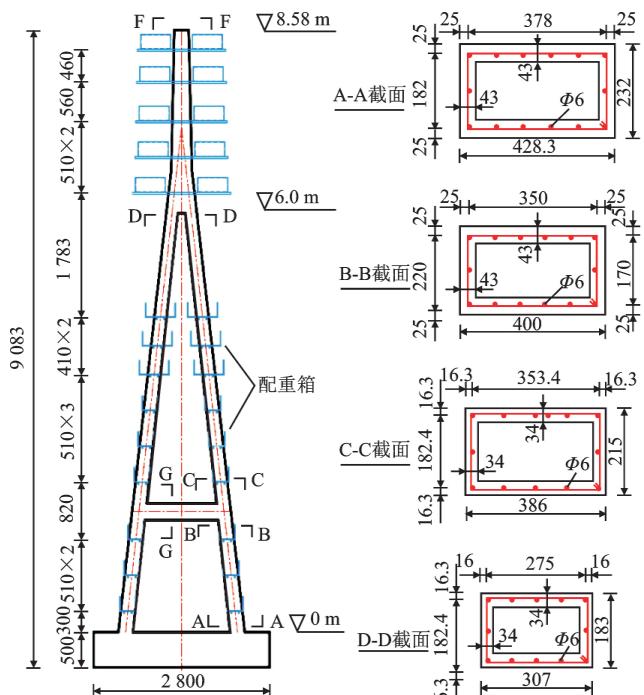
(a) 桥塔 1, 2

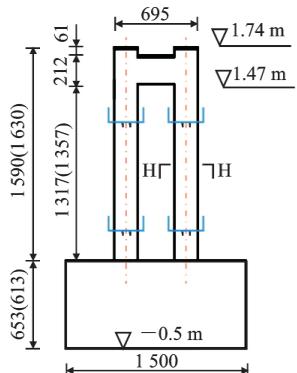
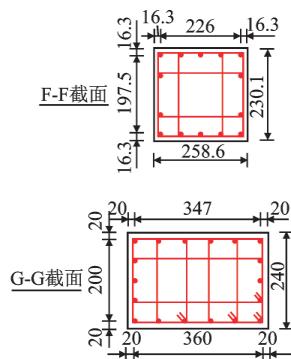
(b) 桥墩 1, 4 ( 括号内尺寸为 2, 3 号桥墩 )

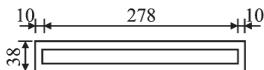
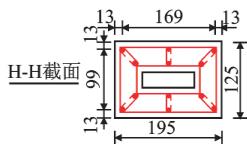
(c) 主梁截面

图 2 关键截面尺寸及配筋（单位：\text{mm}）

Fig.2 Dimensions and Reinforcements of Key Sections (Unit: \text{mm})

图 3 振动台试验模型

Fig.3 Bridge Model for Shake Table Test

1.3 减震体系设计

由于原型桥横向为传统的固定体系，未采用横向减震策略；为了保证试验效果，本文基于全桥缩尺模型，以桥梁新型横向钢阻尼器¹⁰为减震耗能装置，采用非线性时程分析方法，设计了斜拉桥横向减震体系，确定了阻尼器在墩梁、塔梁连接处的力学参数，包括屈服力、弹性刚度、屈后刚度（或硬化率）和位移能力。基于上述力学参数采用 Abaqus 软件设计了试验采用的钢阻尼器²¹，如图 4 所示（1 组），该阻尼器由上、下两部分组成，其中，上半部分由上顶板和侧向钢挡板组成；下半部分由底板、焊接在底板上的三角形钢板、以及半球型传力键组成。其以三角形钢板为耗能构件，具有较好的耗能能力。试验中采用的三角形钢板高 11 \text{cm}，底宽 7 \text{cm}，厚 0.3 \text{cm}。减震体系墩梁、塔梁连接条件为：1, 2, 3 和 4 号桥墩处均为 1 组钢阻尼器和 2 个滑动型球钢支座并联，1, 2 号桥塔处则各布置了 2 组钢阻尼器；图 5 给出了部分墩梁、塔梁连接实况。最后，采用拟静力试验确定了钢阻尼器实际力学参数，表 3 分别给出了桥墩、桥塔处钢阻尼器总的屈服力和弹性约束刚度。

为对比研究和验证减震体系的减震效果，设计了横向固定体系，即墩梁间设置横向固定支座、塔梁间设置横向限位块形成横向固定体系。由于横向全滑动体系非合理抗震体系⁵，而且试验风险过大，因此未设计该试验工况。

图 4 试验模型钢阻尼器实物（1 组）

Fig.4 Photo of One Transverse Steel Damper for Test Model

(a) 墩 - 梁连接 (1 号桥墩处)

(b) 塔 - 梁连接 (1 号桥塔处)

图 5 墩梁、塔梁连接实况

Fig. 5 Photos of Deck-Bent and -Tower Connections

表 3 减震体系横向钢阻尼器力学参数

Table 3 Parameters of Transverse Steel Damper for Isolation System

位置	屈服力/ \text{kN}	弹性刚度/ (\text{kN} \cdot \text{m}^{-1})	位移能力/ \text{cm}	硬化率
桥墩 1, 2, 3, 4	0.74	73	4.7	0.185
桥塔 1, 2	1.48	146	4.7	0.185

2 振动台试验方案

2.1 地震动输入及试验工况

研究表明，近场带脉冲的地震动和远场软弱场地波对长周期桥梁均不利²²。因此，选取 1992 年 Landers 地震中在 Lucerne 台站记录的近场带脉冲的地震动（记为 LCN260）和一条远场软弱场地波（E10，苏通场地波）作为输入，研究和验证斜拉桥横向减震体系的减震效果和抗震性能。图 6 为按时间相似比 (0.169) 压缩后的地震动时程，其中，加速度峰值均调整为 0.5g（g 为重力加速度）。图 7 为时间压缩后的 2 条地震动加速度反应谱比较，其中，阻尼比均为 3\%。表 4 为试验加载工况，地震动输入方向均为横桥向，峰值均为 0.5g。工况 A 研究减震体系在近场带脉冲地震波作用下的行为；加载结束后更换钢阻尼器进行工况 B，研究减震体系在远场地震作用下的行为。其中，工况 A，B 的结构体系、阻尼器布置方案及力学参数均一致。工况 C 为横向固定工况，先输入近场波 LCN260，再输入远场波 E10。需要说明的是，经数值模拟验证，固定体系在 0.5g \text{LCN260} 作用下，结构处于弹性阶段。

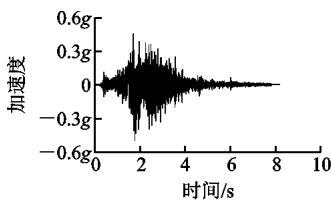
(a) LCN260 加速度时程

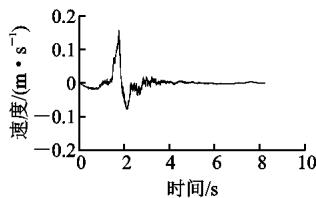
(b) LCN260 速度时程

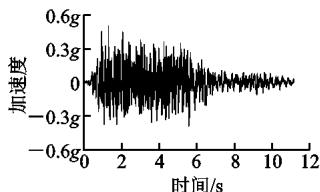
(c) E10 加速度时程

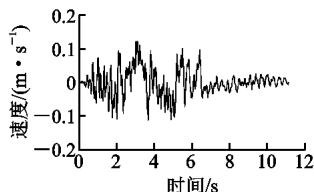
(d) E10 速度时程

图 6 地震动时程

Fig. 6 Time Histories of Ground Motions

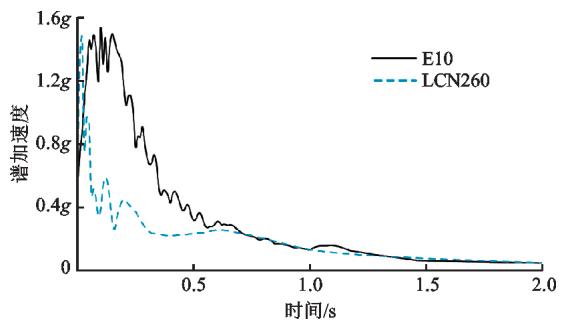
图 7 加速度反应谱（阻尼比 3\%）

Fig. 7 Acceleration Response Spectra with 3\% Damping Ratio

表 4 试验加载工况

Table 4 Test Cases

工况	地震动输入	峰值	输入方向	结构体系
工况 A	白噪声	0.1g	横向	减震体系
	LCN260	0.5g
工况 B	E10	0.5g
工况 C	白噪声	0.1g	横向	固定体系
	LCN260	0.5g
	E10	0.5g

2.2 数据采集方案

沿主梁长度、塔身高度方向布置加速度传感器和位移传感器；沿桥塔一侧塔柱布置应变片和位移计测量塔身截面曲率；桥墩墩底布置应变片测量墩底截面曲率。为测量墩梁、塔梁连接处的地震力，分别于阻尼器底和支座底串联了三向力传感器；由于结构的对称性，仅测量了主梁传递给桥墩 1，2 及桥塔 1 的横向剪力，力传感器的布置可见图 5。采用单向力传感器测量了斜拉索索力。试验数据采用 NI 数采系统采集，采样频率为 256 \text{Hz}。

3 减震体系的减震行为分析

3.1 结构动力特性

选取白噪声作用下，不同体系跨中主梁的横向加速度进行 Fourier 变换，用以识别结构动力特性，并采用半功率带宽法²³，分别计算横向固定体系和横向减震体系的整体阻尼比 \xi_1 和 \xi_2，结果如图 8 所示（其中，H 为 Fourier 幅值，f 为频率）。从图 8 可以看出：固定体系的横向 1 阶频率 f_1 为 0.61 \text{Hz}，对应的周期为 1.64 \text{s}（按时间相似比换算到原桥为 9.70 \text{s}），整体阻尼比为 3.1\%；减震体系的横向 1 阶频率 f_2 为 0.52 \text{Hz}，对应的周期为 1.92 \text{s}，整体阻尼比为 2.3\%。由此可见，横向减震体系进一步延长了结构的周期，可减小结构的地震力响应。另外，需要说明的是，叶爱君等²⁴,²⁵分别给出了苏通大桥横向第 1 阶周期为 9.99 \text{s}, 9.52 \text{s}，与实测结果换算到原桥接近，可验证缩尺模型设计的正确性。

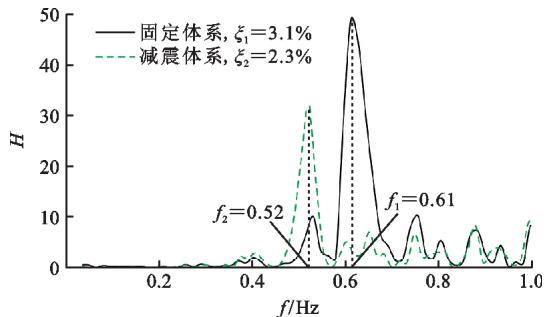
图 8 不同体系结构动力特性比较

Fig. 8 Comparison for Structural Dynamic Characteristic of Different Seismic Systems

3.2 主梁惯性力分布及墩梁、塔梁连接传力

图 9 为近、远场地震作用下横向固定体系和横向减震体系的主梁峰值加速度比较（1/2 主梁长度）。从图 9 可以看出，无论在近场地震还是远场地震作用下，减震体系的主梁峰值加速度均明显小于固定体系，说明地震作用下，减震体系显著减小了主梁传给桥墩和桥塔的惯性力。

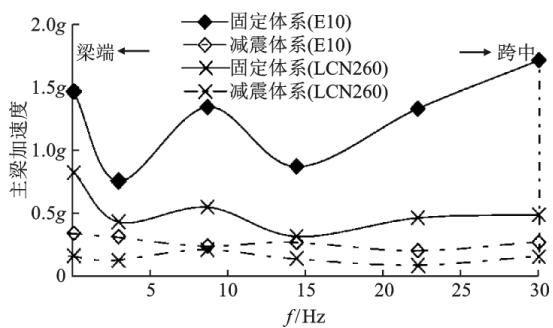
图 9 不同体系主梁横向加速度峰值比较

Fig. 9 Comparisons of Peak Transverse Acceleration Response Along Deck of Different Systems

图 10 为 E10 作用下固定体系和减震体系主梁梁端、跨中加速度时程比较。从图 10 可以看出，相比固定体系，减震体系显著减小了主梁的加速度，从而减小了主梁传递给桥墩和桥塔的惯性力。

表 5 不同体系墩梁、塔梁连接传力比较

Table 5 Comparisons of Peak Lateral Forces at Deck-bent/Tower Connections in Different Systems

墩/塔-梁连接位置	地震动输入	固定体系连接传力 R_1/\text{kN}	减震体系连接传力 R_2/\text{kN}	减震率 R/\%	减震率均值/\%
桥墩1	LCN260	2.44	1.19	51	67
	E10	6.53	1.11	83
桥墩2	LCN260	5.33	1.26	76	84
	E10	11.95	0.95	92
桥塔1	LCN260	7.33	1.94	74	83
	E10	23.11	1.98	91
注：R=(R_1 - R_2) / R_1

表 5 为近、远场地震作用下 2 个体系的墩梁、塔梁连接间的横向地震力比较。从表 5 可以看出，在近、远场地震作用下，相比于传统的固定体系，减震体系墩梁、塔梁间传力均减小了 50\% 以上，最大减小了 92\%。究其原因有两方面：①减震体系延长了结构横向 1 阶周期，减小了主梁横向惯性力；②在地震作用下钢阻尼器率先屈服耗能，主梁传给桥墩、桥塔的地震力为钢阻尼器的设计屈服力和支座摩擦力。因此，减震体系减小了主梁传递给桥墩、桥塔的横向剪力，进而保护了桥墩、桥塔及其基础。

从图 9 和表 5 可以看出，在近场和远场地震作用下，相比于固定体系，减震体系主梁加速度峰值、墩（塔）梁间横向地震力离散性较小，说明该斜拉桥横向减震体系对地震动的敏感性显著下降。

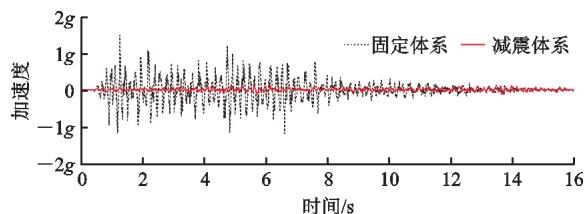
(a) 梁端

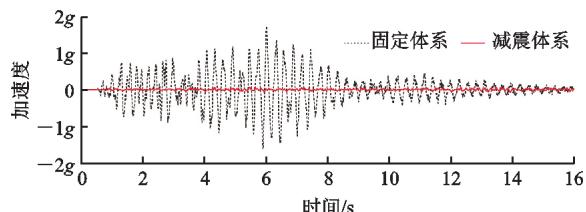
(b) 跨中

图 10 不同体系主梁横向加速度时程比较

Fig. 10 Comparisons for Transverse Deck Acceleration Time Histories of Different Systems

图 11 为 E10 地震作用下，不同体系的主梁跨中位移时程比较。其中，横向固定体系主梁表现出高频振荡的特点，而减震体系主梁则为低频振荡，这也是减震体系能显著减小主梁加速度、墩（塔）梁间横向地震力的原因所在。相对于固定体系，减震体系墩梁、塔梁间设置钢阻尼器后，并未明显增大主梁跨中位移。

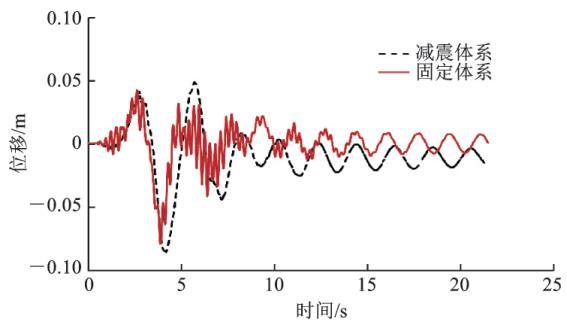
图 11 不同体系主梁跨中位移时程比较

Fig. 11 Comparisons for Displacement Time-histories of Deck at the Mid-span of Different Systems

3.3 塔身位移及截面曲率

图 12 为塔身位移峰值和塔身曲率峰值比较。从图 12 看出，减震体系能一定程度地减小塔身位移和曲率。其中，在近、远场地震作用下，两体系塔身位移峰值均在桥塔交叉点以下，约为桥塔中塔柱 2/3 高度附近。另外，从图 12 可以看出，对于倒 Y 形桥塔，无论减震体系还是固定体系，在近、远场地震作用下，最易损的部位为桥塔横梁上侧截面、交叉点附近截面、中塔柱 2/3 高度附近截面以及塔底。

表 6 不同体系关键截面曲率比较

Table 6 Comparisons for Key-section Curvature of Different Systems Under Near-and Far-field Ground Motions

位置	地震动输入	关键截面曲率	减震率 R/\%	减震率均值/\%
		固定体系 A_1/\text{rad}	减震体系 A_2/\text{rad}
桥墩1墩底	E10	0.0119	0.0084	29.4
	LCN260	0.0060	0.0032	46.7
桥墩2墩底	E10	0.0217	0.0073	66.4
	LCN260	0.0093	0.0029	68.8
塔底	E10	0.0098	0.0070	28.6
	LCN260	0.0030	0.0018	40.0
桥塔横梁上侧截面	E10	0.0129	0.0112	13.2
	LCN260	0.0064	0.0052	18.8
注：R=(A_1 - A_2) / A_1

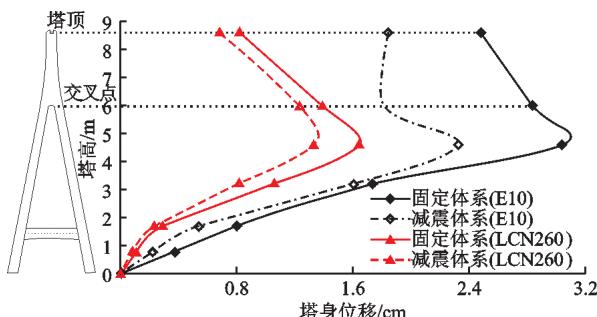
(a) 横向峰值位移

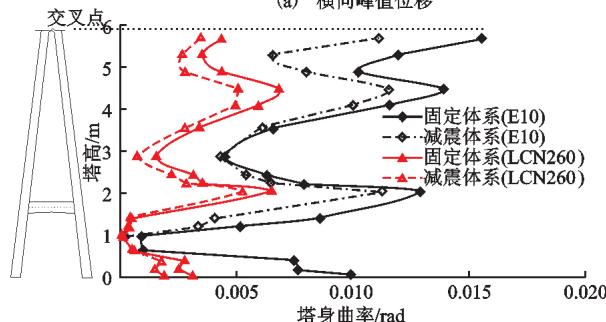
(b) 横向峰值曲率

图 12 不同体系塔身横向峰值位移、曲率比较

Fig. 12 Comparisons for Peak Transverse-curvature and Curvature Along Tower Shaft of Different Systems

表 6 给出了斜拉桥抗震设计中常关注的桥墩墩底、塔底以及横梁上侧塔柱截面曲率比较。从表 6 可以看出，在近、远场地震作用下，减震体系均能显著减小关键截面曲率。其中，桥墩 2 墩底截面曲率平均减小了 67.6\%，塔底截面曲率平均减小了 34.3\%。

3.4 耗能特性分析

为了分析近、远场地震作用下，减震体系的耗能特性，图 13 给出了过渡墩（桥墩 1）的钢阻尼器和滑动型球钢支座的滞回曲线。从图 13 可以看出，钢阻尼器滞回曲线饱满，具备良好的耗能能力；而摩擦型支座的耗能大小依赖于支座竖向反力，耗能能力有限。另外，在近场带脉冲的地震动作用下，阻尼器和支座的滞回圈数较少，表现出明显的脉冲效应，但位移均小于 0.03 \text{m}，在可接受范围内。

图 14 给出了桥墩和桥塔处钢阻尼器在峰值 0.5g 的近场地震 LCN260 作用下的位移时程。从图 14 可以看出，在近场带速度脉冲地震作用下，阻尼器位移呈现明显的脉冲特点。由于地震作用下，钢阻尼器会屈服耗能，导致其震后产生一定的残余位移。钢阻尼器残余位移对结构地震响应的影响，将在后续做进一步的研究。

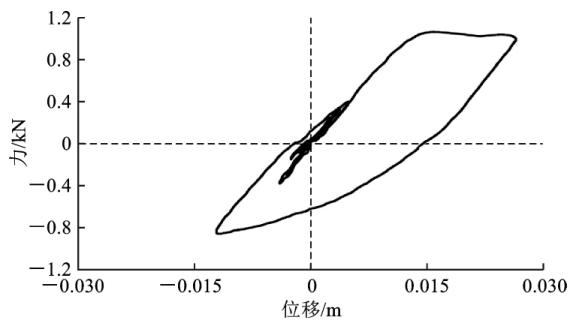
(a) 钢阻尼器 (LCN260)

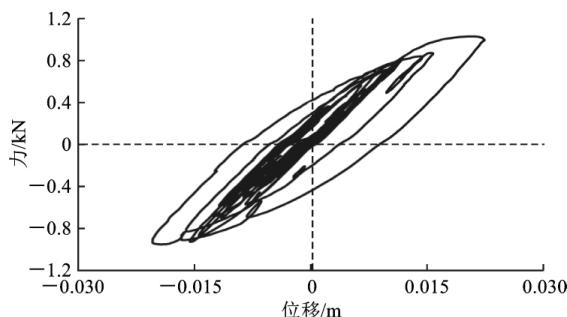
(b) 钢阻尼器 (E10)

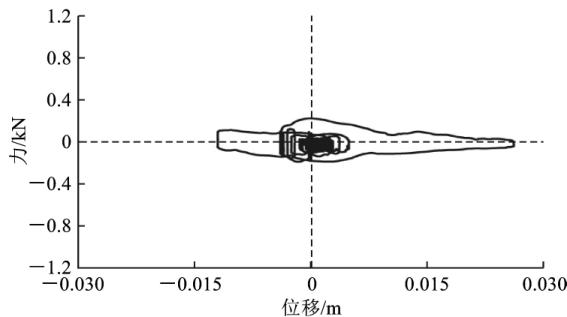
(c) 球钢支座 (LCN260)

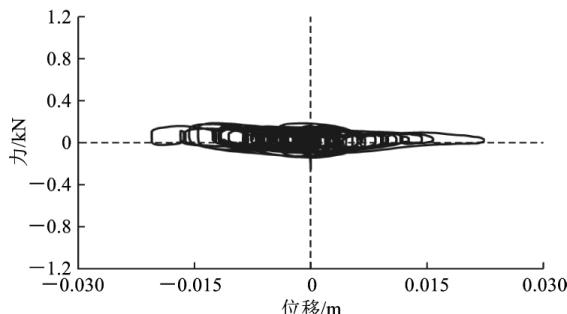
(d) 球钢支座 (E10)

图 13 近、远场地震下横向钢阻尼器、球钢支座滞回曲线 (桥墩 1 处)

Fig. 13 Force-displacement Hysteretic Curves of Transverse Steel Damper and Sliding Spherical Steel Bearings at Bent1-deck Connection Under Different Ground Motions

4 结语

（1）在近、远场地震作用下，减震体系均能减小主梁的峰值加速度，从而显著减小主梁传递给桥墩和桥塔的地震力，且将主梁位移限制在可接受的范围内；减震体系能显著减小塔身位移和曲率峰值、墩底曲率峰值。

（2）对于采用倒 Y 形混凝土桥塔形式的大跨度斜拉桥，在近、远场地震作用下，对于横向固定体系和横向减震体系，桥塔易损部位均为横梁上侧塔柱截面、塔底以及中塔柱的 2/3 高度附近截面。

（3）钢阻尼器滞回曲线饱满，相对于支座的摩擦耗能，其耗能能力更显著；阻尼器滞回特性与地震动有关。另外，在带有速度脉冲的近场地震作用下，阻尼器及支座的位移响应具有明显的脉冲特点。

（4）本文仅代表性地选取一条近场带脉冲地震动和苏通场地波作为输入，且试验未考虑基础对全桥地震需求的影响。试验成果可用于验证大跨度斜拉桥地震反应的数值模拟方法及模型。后续可进一步关注钢阻尼器残余位移对斜拉桥地震反应的影响。

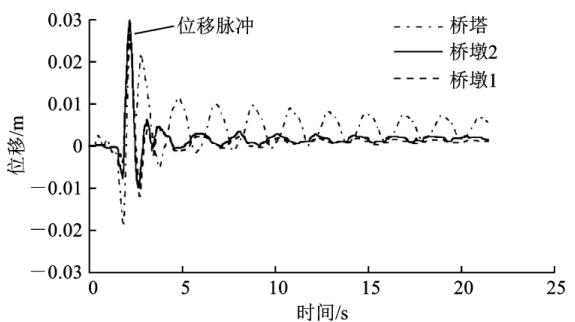
图 14 0.5g-LCN260 作用下不同位置处阻尼器位移时程

Fig. 14 Time-histories of Transverse Steel Damper at Different Locations Under 0.5g-LCN260

---

参考文献

References: