大跨度斜拉桥地震反应谱分析中计算振型数研究
王晓伟^* 叶爱君
(同济大学桥梁工程系,上海 200092)
摘要
《公路桥梁抗震设计细则》规定:进行多振型反应谱分析时,所考虑的振型数应在计算方向上获得 90\% 以上的有效质量。为了研究这条规定在大跨度斜拉桥中的适用性,在介绍推导振型参与系数、振型参与质量系数和振型贡献系数的表达式并比较物理意义的基础上,建立了苏通大桥模型,对上述三个物理量在振型中的分布规律进行了对比分析,同时,根据不同方向的振型参与质量系数达到 90\% 确定不同的计算振型数,进行反应谱分析并分析误差。结果表明:上述规定是合理的,并且对于受水平向与竖向地震联合激励的大跨度斜拉桥,应以竖向振型参与质量系数达到 90\% 所确定的振型数作为计算振型数进行反应谱分析。
关键词
多振型反应谱法,振型参与系数,振型参与质量系数,振型贡献系数,90\% 标准
Computational Mode Number Research in Seismic Response Spectrum Analysis of Long-Span Cable-Stayed Bridge
WANG Xiaowei^* YE Aijun
(Department of Bridge Engineering, Tongji University, Shanghai 200092, China)
Abstract
On the basis of Guidelines for Seismic Design of Highway Bridges, the vibration mode number considered in mode-decomposition response spectrum analysis should get more than 90\% of the effective mass in the calculation direction. To study the applicability of this standard in long-span cable-stayed bridges, three physical quantities on modal participation were introduced and compared. Then, a computational model of Sutong Bridge was set up to identify the different calculating vibration mode number in terms of the modal participation mass ratio reaching 0.9 in different direction, so as to conduct response spectrum analysis and analyze the error. The result shows that, to conduct response spectrum analysis for a long-span cable-stayed bridge under both horizontal and vertical seismic excitation, the vibration mode number derived from the vertical modal participation mass ratio reaching 0.9 should be taken as the calculating vibration mode number.
Keywords
mode-decomposition response spectrum method, modal participation factor, modal participation mass ratio, modal contribution ratio, 90\% criterion
1 引言
多振型反应谱法是桥梁抗震分析中最常用的方法之一,该方法的优点在于只需要取前几阶或几十阶振型即可进行整个结构的动力反应分析,并得到工程可接受的合理结果。我国的《公路桥梁抗震设计细则》规定:用多振型反应谱法计算时,所考虑的振型阶数应在计算方向获得 90\% 以上的有效质量(简称“ 90\% 标准”)。事实上,这条规定参考《建筑抗震设计规范》而得,目前在建筑结构抗震领域,国内外学者对反应谱振型分解法中振型数的确定进行了一些研究3,4,5,6,7,对多振型反应谱法中计算振型数的确定原则进行了验证与改进。相比之下,在桥梁工程抗震领域,考虑到桥梁结构的非规则性,规范中确定计算振型数的方法是否合理值得质疑,国内外少有关于这方面的研究文献,设计人员对振型参与系数、振型参与质量系数和振型贡献系数等易混淆的概念尚存在认识上的模糊性,而设计所使用的一些结构分析程序一般采用有效质量(或称振型参与质量)来确定抗震动力分析所需的振型数8,9。本文首先分析讨论了振型参与系数的性质,对振型参与质量系数、振型贡献系数进行了理论推导,结合苏通大桥工程实例,对振型参与系数、振型参与质量系数和振型贡献系数的各振型分布情况做了比较分析,探讨大跨度斜拉桥地震反应谱分析中计算振型数的确定方法,并进行误差分析,以此评价《公路桥梁抗震设计细则》中关于反应谱振型分解法的“ 90\% 标准”的合理性。
2 振型参与系数、振型参与质量系数与振型贡献系数10,11
在水平向地震作用下,多自由度体系(假设自由度为 n )的运动微分方程可表示为
式中,[M],[C],[K] 分别为多自由度体系的质量矩阵、阻尼矩阵和刚度矩阵;\{\delta\} 为各自由度对地面的相对位移列向量,是关于时间 t 的函数;\{I\} 为位移变化向量,表示由于施加单位支座静位移引起的每个结构自由度的位移,其中元素只有 0 或 1;\ddot{\delta}_g(t) 为地面输入地震动加速度。
将位移列向量 \{\delta(t)\} 分解为
式中,[\varphi]=[\{\varphi\}_1, \{\varphi\}_2, \ldots, \{\varphi\}_n] 为振型矩阵,\{\varphi\}_i 为第 i 阶振型列向量;\{Y(t)\}=[Y_1(t), Y_2(t), \ldots, Y_n(t)], Y_i(t) 称为振型坐标,为广义坐标。
通过对无阻尼多自由度系统的推导可知振型满足正交条件:
对于比例阻尼矩阵,满足
将式 (2) 代入式(1),再以矩阵 [\varphi]^T 左乘式(1),并利用振型的正交条件,可得解耦的 n 个的振动方程,其中第 i 阶振型的振动方程如下:
上式两边再同时除以 \{\varphi\}_i^T [M]\{\varphi\}_i (常数),则有
其中:
式中,\gamma_i 为第 i 阶振型的振型参与系数。
分析式(7)可知:\gamma_i 随着 \{\varphi\}_i 形式不同而变化,对同一个振型而言,\gamma_i 不是唯一确定的;\gamma_i 有量纲,其量纲为长度的倒数 (L^{-1});通常情况下,结构动力反应的各阶振型参与系数之和不等于 1,即 \sum_{i=1}^{n} \gamma_i \neq 1。
因此,理论上仅仅根据结构的振型参与系数不能合理地反映各阶振型对于结构动力反应的贡献。
假设 S_{A,i} 为第 i 阶振型的周期对应的加速度反应谱的谱值,于是,第 i 阶振型产生的惯性力最大值为
对于某一水平方向上,第 i 阶振型各自由度惯性力最大值的代数和 |F_{I,\max}|_i 为
式中,令 \{\varphi\}_i^T [M]\{\varphi\}_i = M_i 为第 i 阶振型的广义质量。假设下式成立:
于是有
式中,M_{total} 为所有自由度的总质量,且结构整体加速度 S_A = S_{A,i} \equiv 1,则:
定义 \gamma_i^2 M_i 为第 i 阶振型的振型参与质量,得前 j 阶 (j < n) 振型参与质量系数 r_j 为
定义 \kappa_i 为第 i 阶振型的振型贡献系数。
从式(12)、式(13)可知,r_i 唯一确定,不随 \{\varphi\}_i 形式不同而改变;r_i 无量纲且 \sum_{i=1}^{n} r_i = 1。
故理论上,振型参与质量系数 r 比振型参与系数 \gamma 更准确地反映各阶振型对于结构总反应的贡献。但是振型参与质量系数 r 并未考虑实际反应谱输入的影响,而振型贡献系数 \kappa 则考虑了实际反应谱输入的影响,确切地反映出对结构反应起主要贡献的振型。
式(9)中第 i 阶振型各自由度惯性力最大值的代数和 |F_{I,\max}|_i 有如下解释:
(1)对于普通建筑结构,|F_{I,\max}|_i 为第 i 阶振型的基底剪力,对建筑结构抗震设计起控制作用,即说明振型参与质量系数在建筑结构抗震设计中意义明确。
(2)对于大跨度斜拉桥,|F_{I,\max}|_i 为某一方向第 i 阶振型各桥墩底剪力的代数和,显然,对于抗震设计,存在各桥墩底剪力分配问题,因此这个物理量在桥梁的抗震反应谱分析中存在一定的模糊性。此外,根据式 (8) 可知,桥梁各墩的实际反应还与桥梁的质量分布和振型形状有关。
因此,对振型参与质量系数在桥梁抗震设计中的适用性进行验证评价有现实意义。
3 计算模型与地震输入
3.1 计算模型
图 1 显示了以苏通公路长江大桥为背景工程,由通用有限元软件 SAP2000 建立的三维有限元模型。其中,主梁、塔、边墩用梁单元模拟,考虑恒载轴力引起的几何刚度的影响;主梁节点和斜拉索吊点主从相连;斜拉索用桁架单元模拟,并考虑垂度效应和恒载引起的几何刚度的影响;主梁与主塔纵向相对自由,横向主从连接;主梁与边墩纵向相对自由,横向主从连接。
图 1 苏通大桥三维有限元模型
3.2 地震输入
本文采用江苏省地震工程研究院提供的苏通大桥桥址处的地震动参数作为基本地震输入,图 2 显示了阻尼比 5\%、地震重现期 2500 年的地震加速度反应谱曲线。
在本例中,X, Y 方向对应水平向设计加速度反应谱,Z 方向对应竖直设计加速度反应谱。具体而言,研究计算振型数的确定及误差分析时,分别考虑 X 与 Z 方向,Y 与 Z 方向的设计加速度反应谱组合输入。
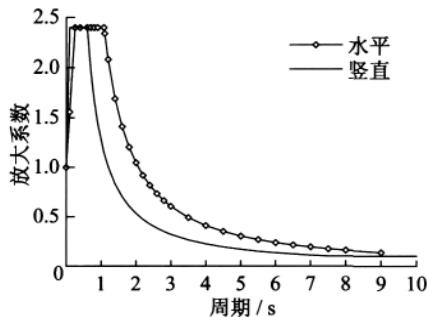
图 2 加速度反应谱曲线
4 振型参与系数、振型参与质量系数和振型贡献系数分布规律分析
为比较振型参与系数、振型参与质量系数和振型贡献系数这三个物理量,分别对苏通大桥的动力计算模型 X, Y, Z 方向单独输入对应的设计加速度反应谱,进行模态分析得振型阶数为 400 阶情况下的振型参与系数、振型参与质量系数和振型贡献系数(结合加速度反应谱值)的分布情况,为便于比较,将振型参与系数在数值上取绝对值,图 3—图 5 显示了三者在纵向、横向和竖向的分布情况。
(1)比较图 3(或图 4、图 5)中的 (a),(b),(c)
纵向、横向输入,前 80 阶振型对反应起主要控制作用;而竖向输入对反应起主要控制作用的振型则出现在 250 阶左右。也即说明苏通大桥的纵向、横向剪力和弯矩主要受前 80 阶振型控制,而竖向轴力主要受 110 阶之后,特别是 250 阶左右的振型的影响比较大。
(2)比较图 3—图 5 中的图 (a)(或图 (b)、图 (c))
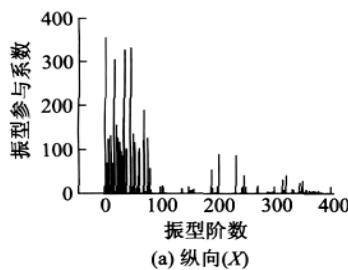
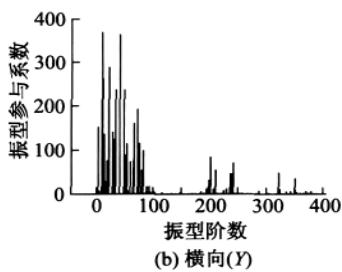
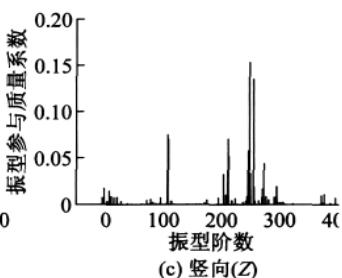
图 3 振型参与系数 \gamma 分布图
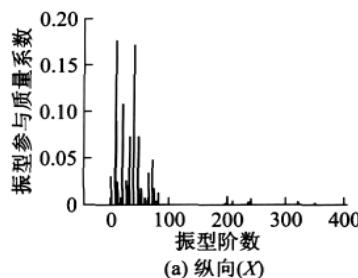
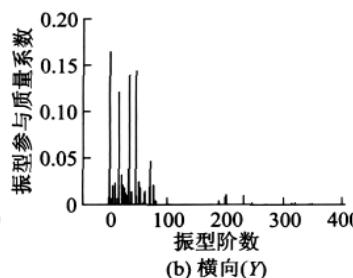
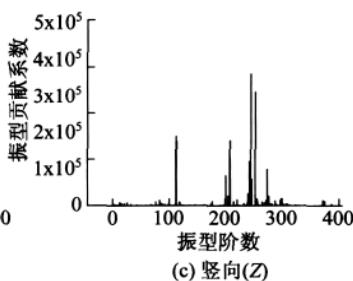
图 4 振型参与质量系数 r 分布图
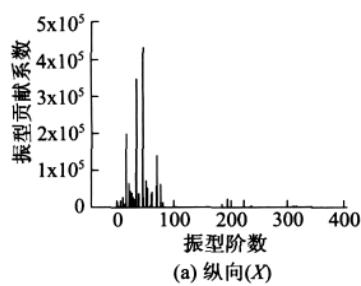
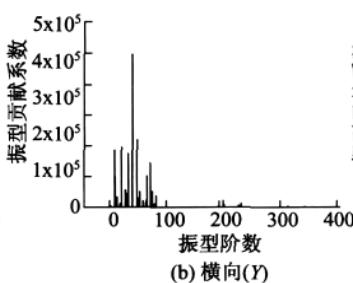
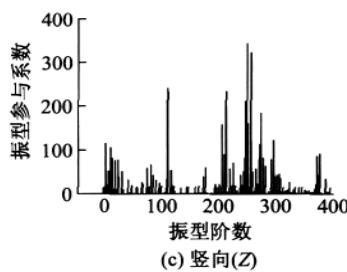
图 5 振型贡献系数 \kappa 分布图
某一方向(纵向、横向或竖向)地震力输入下,从振型参与系数到振型参与质量系数再到振型贡献系数的分布规律,有一种“过滤”的效果:仅仅从振型参与系数的分布规律很难准确判断哪些振型对反应起到了决定性的作用,哪些振型的贡献可以忽略,而根据振型参与质量系数的分布规律则可以较准确地判断出不同振型的贡献程度,振型贡献系数的分布规律则进一步确切地反映出对结构反应起最主要控制作用的振型阶数,更多对反应贡献较小的振型被忽略,达到了很好的“过滤”效果,这对于快速找出桥梁体系振型反应谱分解法中的主要控制振型提供了高效的方法,比如从图 5 可以看出纵向、横向地震力输入下的主控振型(惯性力最大)分别为第 46, 40 阶,竖向输入下的主控振型为第 245 阶。同时,振型参与质量系数与振型贡献系数的分布规律相似度较高,说明现行规范中利用振型参与质量系数的“ 90\% 标准”判断计算振型数有实际的依据。
由以上的比较分析说明振型参与系数并不能很好地反映对反应起主要贡献的振型,而振型参与质量系数和振型贡献系数这两个物理量能较好地反映出对结构反应起主要贡献的振型。文章将主要根据振型参与质量系数进行计算振型数的确定及误差分析。
5 计算振型阶数确定及误差分析
5.1 计算振型阶数的确定
《公路桥梁抗震设计细则》规定:用多振型反应谱法计算时,所考虑的振型阶数应在计算方向获得 90\% 以上的有效质量,对于非规则桥梁,进行多振型反应谱法分析时,应根据结构特点,考虑足够的振型。
为确定大跨度斜拉桥反应谱分析中的计算振型阶数,先取前 400 阶振型对苏通大桥有限元结构模型进行反应谱分析,得到结构控制断面的内力,根据不同方向的振型参与质量系数达到 90\% 确定计算振型阶数,以此计算振型阶数再次进行反应谱分析,得到结构相同控制断面的内力,并与前 400 阶振型参与的反应谱分析内力结果进行比较。
表 1 列出了前 400 阶振型参与的反应谱分析中纵向、横向和竖向振型参与质量系数达到 90\% 时所对应的振型阶数。其中,输入方式为“纵向 + 竖向”时,考虑纵向、竖向的振型参与质量系数 (\text{sumUX}, \text{sumUZ});输入方式为“横向 + 竖向”时,考虑横向、竖向的振型参与质量系数 (\text{sumUY}, \text{sumUZ})。
| 输入方式 | \text{sumUX} | \text{sumUY} | \text{sumUZ} | 计算振型阶数 |
|---|---|---|---|---|
| 纵向+竖向 | 0.90 | - | 0.07 | 70 |
| 纵向+竖向 | 0.99 | - | 0.91 | 270 |
| 横向+竖向 | - | 0.92 | 0.07 | 72 |
| 横向+竖向 | - | 0.99 | 0.91 | 270 |
表 1 400 阶振型下计算振型阶数的确定
5.2 纵向与竖向地震联合激励下主塔、边墩各控制断面内力比较
结构在纵向与竖向地震联合激励下,求得纵向、竖向振型参与质量系数分别达到 90\% 时的计算振型阶数( 70 阶、270 阶)所对应的内力,将其与 400 阶振型阶数求得的内力相比较,如表 2 显示,从中可以看出:
| 内力 | 工况 | 苏通大桥受力关键部位控制断面内力及误差比较 |
|---|---|---|
| 主塔底 | ||
| 轴力P/kN | ① 70 阶 | 8.44\times 10^4 |
| ② 270 阶 | 7.57\times 10^4 | |
| ③ 400 阶 | 7.55\times 10^4 | |
| 轴力误差/% | $ | \text{①} - \text{③} |
| $ | \text{②} - \text{③} | |
| 剪力Q_X/kN | ① 70 阶 | 3.28\times 10^4 |
| ② 270 阶 | 3.15\times 10^4 | |
| ③ 400 阶 | 3.15\times 10^4 | |
| 剪力误差/% | $ | \text{①} - \text{③} |
| $ | \text{②} - \text{③} | |
| 弯矩M_Y/(kN·m) | ① 70 阶 | 2.68\times 10^6 |
| ② 270 阶 | 2.69\times 10^6 | |
| ③ 400 阶 | 2.69\times 10^6 | |
| 弯矩误差/% | $ | \text{①} - \text{③} |
| $ | \text{②} - \text{③} |
表 2 70 阶、270 阶与 400 阶振型阶数下各控制断面内力比较 (纵向 + 竖向输入)
注: 表中 X 方向为纵桥向,Y 方向为横桥向,L+V 表示纵向及竖向地震联合激励。
(1) 纵向振型参与质量系数达到 90\% 时,主塔塔底、下横梁下侧和过渡墩底、辅助墩底的纵向弯矩 M_Y、纵向剪力 Q_X,误差均小于 5\%,这些断面基本符合“ 90\% 标准”;而主塔下横梁上侧、交叉点上下侧和过渡墩底的纵向弯矩 M_Y 或纵向剪力 Q_X 误差相对较大,这些断面的内力不应根据纵向振型参与质量系数达到 90\% 的计算振型数来计算。
(2) 纵向振型参与质量系数达到 90\% 时,主塔上交叉点的轴力误差极大,主要是由于轴力对高阶振型的敏感性所导致的,其他控制断面的轴力误差亦说明了这一原因;下横梁上侧的剪力误差很大,考虑到水平向内力主要受前 80 阶振型控制,并且竖向地震输入对水平向反应无影响,因此可知,惯性力在各桥墩的分配问题导致误差较大。
(3) 竖向振型参与质量系数达到 90\% 时,主塔、辅助墩和过渡墩处各控制断面的竖向轴力 P 的误差较小,说明竖向内力在这些断面符合“ 90\% 标准”。
(4) 大跨度斜拉桥在纵向与竖向地震联合激励下,进行多振型反应谱分析时,应以竖向振型参与质量系数到达 90\% 确定计算振型阶数。
5.3 横向及竖向地震联合激励下主塔、边墩各控制断面内力比较
以相同的方式研究横向及竖向地震联合激励下的情况,即以横向、竖向振型参与质量系数达到 90\% 时确定的计算振型阶数( 72 阶、270 阶)算得的内力与 400 阶振型阶数算得的内力相比较,如表 3 所示。
| 内力 | 工况 | 苏通大桥受力关键部位控制断面内力及误差比较 |
|---|---|---|
| 主塔底 | ||
| 轴力P/kN | ① 72 阶 | 2.86\times 10^5 |
| ② 270 阶 | 2.77\times 10^5 | |
| ③ 400 阶 | 2.77\times 10^5 | |
| 轴力误差/% | $ | \text{①} - \text{③} |
| $ | \text{②} - \text{③} | |
| 剪力Q_Y/kN | ① 72 阶 | 3.74\times 10^4 |
| ② 270 阶 | 3.52\times 10^4 | |
| ③ 400 阶 | 3.52\times 10^4 | |
| 剪力误差/% | $ | \text{①} - \text{③} |
| $ | \text{②} - \text{③} | |
| 弯矩M_X/(kN·m) | ① 72 阶 | 1.25\times 10^6 |
| ② 270 阶 | 1.23\times 10^6 | |
| ③ 400 阶 | 1.23\times 10^6 | |
| 弯矩误差/% | $ | \text{①} - \text{③} |
| $ | \text{②} - \text{③} |
表 3 72 阶、270 阶与 400 阶振型阶数下各控制断面内力比较(横向 + 竖向输入)
注: 表中 X 方向为纵桥向,Y 方向为横桥向,T+V 表示横向及竖向地震联合激励。
(1) 横向振型参与质量系数达到 90\% 时,主塔下横梁下侧、近塔辅助墩底的横向弯矩 M_X、横向剪力 Q_Y 误差均小于 5\% 左右,基本符合“ 90\% 标准”;而其他主要控制断面的内力不应根据纵向振型参与质量系数达到 90\% 的计算振型数来计算。
(2) 横向振型参与质量系数达到 90\% 时,主塔上交叉点上侧的轴力误差极大是因为轴力对高阶振型的敏感性所造成的;下横梁下侧、交叉点下侧的水平剪力、弯矩的误差则是由于惯性力在各桥墩的分配问题引起的,同时,辅助墩底、过渡墩底的剪力、弯矩误差亦反映了导致误差的这一原因。
(3) 大跨度斜拉桥在横向与竖向联合地震激励下,进行多振型反应谱分析时,应以竖向振型参与质量系数到达 90\% 确定计算振型数。
6 结论
本文介绍和比较了振型参与系数、振型参与质量系数和振型贡献系数物理量的性质,比较了这三个系数在实际大跨度斜拉桥中纵向、横向和竖向的不同分布情况,并根据规范要求确定计算振型数来进行误差分析,得出了以下结论:
(1)振型参与系数并不能很好地反映各阶振型对反应的贡献,而振型参与质量系数和振型贡献系数这两个物理量较好地反映了各阶振型对反应的贡献。规范使用振型参与质量系数表征各阶振型对于结构反应的贡献是基本合理的。
(2)对于大跨度斜拉桥,由水平向地震动引起的结构反应(如剪力、弯矩)往往由较低阶的振型贡献控制,而由竖向地震动引起的结构反应(如轴力)往往由高阶振型的贡献控制。这直接决定了大跨度斜拉桥的计算振型数较高。
(3) 对于大跨度斜拉桥,由于惯性力在各桥墩的分配问题,在水平向和竖向地震联合激励下,仅按水平向计算振型数的“ 90\% 标准”可能会导致局部构件,如主塔交叉点上下侧、下横梁上侧、边墩等部位的误差偏大。
(4)验证了《公路桥梁抗震设计细则》的“ 90\% 标准”是合理的,并且对于受水平向及竖向地震联合激励的大跨度斜拉桥,应以竖向振型参与质量系数达到 90\% 所确定的振型阶数作为计算振型数来进行反应谱分析。
参考文献
重庆交通科研设计院. JTG/F B02-01—2008,公路桥梁抗震设计细则 [S]. 北京:人民交通出版社,2008. China Merchans Chongqing Communications Research & Design Institute Co., Ltd. JTG/FB02-01-2008, Guidelines for Seismic Design of Highway Bridges [S]. Beijing: China Communication Press, 2009. (in Chinese)
中华人民共和国建设部. GB50011—2001 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2002. Ministry of Construction of the People's Republic of China. GB50011—2001 Code for Seismic Design of Buildings [S]. Beijing: China Architecture and Building Press, 2002. (in Chinese)
史铁花, 韦承基. 振型分解法中合理振型数的确定 [J]. 建筑科学, 2002, 18(2):29-31. Shi TH, Wei C J. Decision of reasonable mode number in mode-superposition method [J]. Building Science, 2002, 18(2): 29-31. (in Chinese) ↩
卞朝东, 李爱群, 娄宇, 等. 高层连体结构振型及其参与系数的分析 [J]. 建筑科学, 2002, 18(4): 20-24. Bian C D, Li A Q, Lou Y, et al. Analysis of vibration modes and participating coefficients for high-rise connecting structure [J]. Building Science, 2002, 18 (4): 20-24. (in Chinese) ↩
李广俊, 李爱群. 关于结构振型参与系数和振型贡献的分析 [J]. 防灾减灾工程学报, 2009, 29(5):485-490. Sun G J, Li A Q. Analysis of mode participation factor and modal contribution of structures [J]. Journal of Disaster Prevention and Mitigation Engineering, 2009, 29(5):485-490. (in Chinese) ↩
李世翠, 聂大亮, 孙斌. 抗震设计合理振型数研究 [J]. 山东建筑大学学报, 2007, 22(5):395-398. Li S C, Nie D L, Sun B. The reasonable mode num research in the seismic design [J]. Journal of Shandong Jianzhu University, 2007, 22 (5): 395-398. (in Chinese) ↩
Wilson E L. Three Dimensional Static and Dynamic Analysis of Structures [M]. USA: Computer and Structures Inc., 2002: 185-186. ↩
ETABS User's Manual [M]. USA: Computer and Structures Inc., 1999. ↩
SAP2000 User's Manual [M]. USA: Computer and Structures Inc., 1995. ↩
Chopra A K. Dynamics of structures [M]. USA: Prentice-Hall, 2000. ↩
Clough R W, Penzien J. Dynamics of structures [M]. 2nd Edition. USA: McGraw-Hill, 1995. ↩