王晓伟,叶爱君,沈星,庞于涛
(同济大学,土木工程防灾国家重点实验室,上海 200092)
摘要:在大跨度桥梁中,边墩的竖向恒载与中墩相比往往较小,导致支座滑动摩擦力较小,因此,摩擦型耗能减震支座无法有效控制地震位移。针对以上问题,提出了滞回型钢阻尼器和滑动支座配合使用的桥梁边墩减震体系。然后,以一座大跨度钢桁架拱桥为例,建立了全桥有限元模型,以支座位移、墩底弯矩以及拱脚立柱的应力为工程需求参数,采用云图法建立概率地震需求模型,分析了该大跨度桥梁的边墩横向地震易损性。结果表明,采用滞回型钢阻尼器和滑动支座的桥梁边墩减震体系可有效降低桥梁上、下部结构各主要控制部位的横向地震易损性。
关键词:桥梁边墩;横向减震体系;滞回型钢阻尼器;地震易损性分析;损伤指标
中图分类号:U442.5+5
文献标志码:A
Fragility Analysis on Transversal Isolation System for Outer Piers of Long Span Bridges
WANG Xiaowei, YE Aijun, SHEN Xing, PANG Yutao
(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: In common design of long span bridges, dead load on outer piers was much smaller than that on inner piers. As a result, under seismic excitation, energy dissipation for friction pendulum bearings on outer piers was not effective. In this regard, a new transversal isolation system consisting of a hysteretic damper and sliding bearing was proposed. After that, the effectivity of this system was validated by a modern steel trussed arch bridge using fragility function. Displacement of sliding bearings, bending moment of outer piers and stress on the arch springing were taken as the engineering demand parameters. Cloud method was applied to build the probabilistic demand seismic model. The generated fragility curves show that the proposed transversal isolation system performs quite well under potential earthquakes.
Key words: bridge outer pier; transversal isolation system;
hysteretic damper; fragility analysis; damage indices
对于大跨度桥梁的边墩,目前工程界常用的横向抗震体系主要有两类:(1)采用固定支座的全限位体系,限制墩、梁横向相对位移,虽然可以保障正常使用中边墩的横向稳定性,但在潜在地震下,支座和下部结构都将承受巨大的水平力,可能导致墩柱和基础产生不可修复的损伤;(2)采用摩擦摆式支座的减隔震体系,即利用支座的摩擦耗能达到减震目的,但由于悬臂施工等原因,成桥后边墩的竖向恒载往往远小于中墩,导致边墩上的支座滑动摩擦力较小,无法充分发挥摩擦摆式支座的耗能特性,这种体系虽然可以保障墩柱和基础的完好,但同时不可避免地付出了支座横向位移过大的代价。因此,亟待提出一种合理的桥梁边墩横向减震体系,而选用何种减震装置是该体系的关键。虽然粘滞液压阻尼器具有良好的耗能减震能力,但通常应用在纵桥向1;对于桥梁横向而言,为了适应桥梁纵向的温度变形等要求,粘滞液压阻尼器往往需要设置销铰,构造较复杂,在纵桥向变形较大时,阻尼器与横桥向的夹角可能影响传力路径。相比之下,利用钢材稳定的力学特性所开发的滞回型阻尼器已在不同结构上得到了一定的运用2,3,4,5,6,7,8,9,但现有的能满足纵向变形的钢阻尼器往往需要在桥墩顶面开槽,影响桥梁结构的设计。因此,本文提出一种桥梁横向减震体系,并采用合理的评估方法验证其适用性。该体系采用位移能力较大、传力明确、构造简单的钢阻尼器与滑动支座配合使用。
地震易损性分析是桥梁减震体系合理性的有效评估方式,可对桥梁在受到地震荷载作用时的损伤程度进行评估,并将地震动输入强度与结构的损伤指标有机地建立联系,从宏观上把握结构在各种潜在地震下损伤的可能性。Casciati 等10分析了滞回型耗能装置对典型斜拉桥纵向地震易损性的影响;Padgett 等11,12研究了采用不同抗震加固措施(橡胶减震支座、纵向连梁装置、横向挡块等)的典型城市高架多跨简支梁桥的地震易损性;Zhang 和 \mathrm{Huo}13 进行了采用不同减震装置(橡胶支座、铅芯橡胶支座、摩擦摆式支座 ) 的城市高架连续梁桥中墩的地震易损性分析。以上研究或针对桥梁纵向地震易损性,或针对简支梁桥各部件、连续梁桥中墩的地震易损性,尚缺乏针对桥梁边墩横向减震体系的地震易损性分析。
本文首先简介地震易损性分析方法,然后以某大跨度钢桁架拱桥为背景,介绍所提出的桥梁边墩横向减震体系。然后,基于地震易损性分析方法,选取 36 条实际地震波,对不同的边墩横向抗震体系进行了非线性时程分析,比较分析不同体系下桥梁横向的地震易损性,验证所提出的边墩横向减震体系的合理性。
1 地震易损性分析方法
地震易损性分析需要首先建立概率地震需求模型,常用的两种方法是增量动力(IDA)法和“云图法”。IDA 方法通过调整地震波的地震动强度(I_{\mathrm{M}}),经过大量的动力时程分析,获得结构构件在不同地震动强度下的地震反应,从而建立概率地震需求模型。“云图法”直接选取不同地震动强度的地震波,不需要经过地震动调幅,通过动力时程分析获得概率地震需求模型。与 IDA 方法相比,“云图法”能够减小动力时程分析的计算量,且能避免对实测地震动进行调幅。因此本文采用“云图法”建立地震需求模型。
假定工程需求参数(EDP)满足正态分布14,15,其均值 \mu_{\mathrm{D}} 与地震动强度 I_{\mathrm{M}} 呈幂次方(或对数线性)关系:
式中,a 和 b 均为常数。
地震需求的方差 \beta_{\mathrm{D}}14,15 可确定如下:
式中,S_{\mathrm{Di}} 为不同地震动强度 I_{\mathrm{M}} 下的地震需求。
在获得各工程需求参数的概率地震需求模型的基础上,可进一步得到结构构件的地震易损性曲线。地震易损性指的是给定地震动强度水平 I_{\mathrm{M}} = x 的条件下,结构的地震需求 D 超过损伤指标 C 的条件概率:
式中,地震需求 D 是一个随机变量,通常认为它服从对数正态分布,由此可得构件失效概率 P_{\mathrm{f}} 为:
式中, \Phi (\cdot) 为标准正态分布函数。
与传统的确定性方法相比,地震易损性方法可对结构在其生命周期内不同水平的地震动下发生不同损伤的可能性,具有更全面的评价结果。
2 大跨度桥梁边墩横向减震体系
2.1 工程背景及结构体系
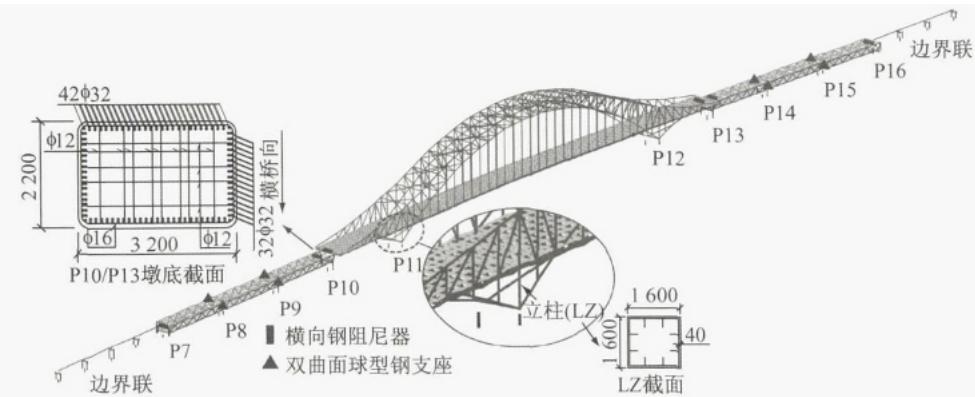
以某近海大跨度钢桁架拱桥为工程背景,主桥为 (80 + 336 + 80)\mathrm{m} 的中承式双层钢桁拱桥,左右各连 3\times 72\mathrm{m} 的钢桁架水上引桥,水上引桥与岸上引桥相连。图 1a 为桥梁正常使用状态下的横向约束体系 (记为 T-R)。图中,\mathrm{P7\sim P16} 表示桥墩编号。该横向约束体系在设计地震下存在的主要抗震问题是:水上引桥各墩、主引桥过渡墩墩底及其基础的需求很大,多数桩基础进入屈服状态,不满足设计规范16的要求。上述问题也是大多数大跨度桥梁在横桥向所面临的共同问题。
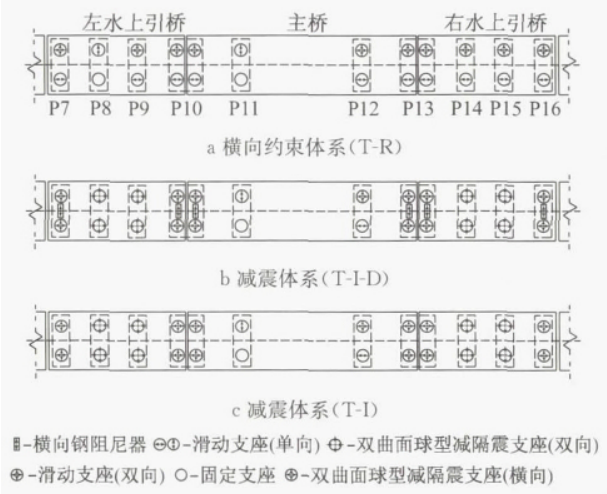
图 1 横向约束体系及减震体系布置
Fig.1 Layout of the lateral restraint and isolation systems
针对常规体系的问题,拟采用减震体系,而选取合理的减震装置是桥梁减震设计的关键。目前适用于大跨度桥梁的减震装置包括:铅芯橡胶支座、高阻尼橡胶支座、滑动摩擦型减震支座、双曲面球型减震支座、金属阻尼器、粘滞液压阻尼器等。考虑到工程背景的临海特征,橡胶类减震装置在潮湿的环境中易受氧化作用而加速老化破坏。此外,减震装置应具备一定的恢复力,以保证地震下上下部结构的整体完整性,防止落梁,故不宜采用不具备恢复力的滑动摩擦型减震支座。相比之下,具备自恢复力的双曲面球型减震支座是较为合理的选择。该实例的中墩采用双曲面减震支座,利用地震下中墩支座的巨大摩擦力耗能。但是,对于边墩,由于支座恒载反力相对很小,双曲面减震支座不具备较好的耗能能力。
鉴于以上分析,有必要提出一种专门适用于桥梁边墩横向的减震装置,既具备强大的耗能减震能力,又能满足正常使用条件下纵桥向的变形。在综合考虑功能性和经济性的前提下,采用三角形钢板的钢阻尼器是一种合理的选择17。图 2 为钢阻尼器与滑动支座组成的桥梁边墩横向减震体系图示,该体系的核心部件为横向钢阻尼器,利用三角形钢板较大的弹塑性变形能力耗散地震能量。图 2c 中,h,w,t 分别为单块三角形板的高,宽,厚。钢板底部焊接在下底板并由螺栓栓接到墩顶、盖梁或系梁,上顶板挡块焊接在上顶板并通过螺栓栓接于主梁底。上部结构的横向水平地震力通过半球型传力键传至三角形钢板顶点。该半球型传力键:(1)可保证三角形钢板在变形较大的情况下仍能保持原有的传力路径;(2)在顺桥向可以自由滑动,满足桥梁正常使用功能条件下主梁的纵向位移要求。该减震体系可在减小下部结构地震反应和控制上部结构地震位移这两方面找到平衡点。
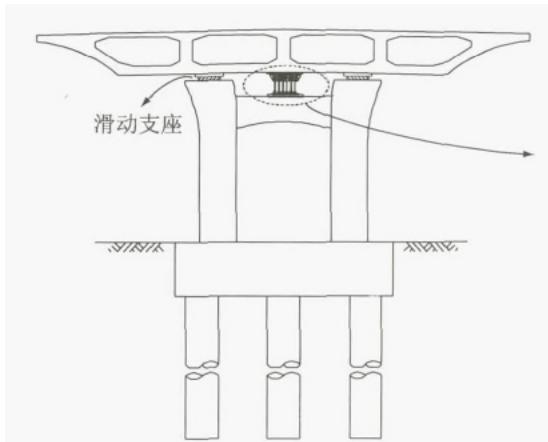
a 横向减震体系布置
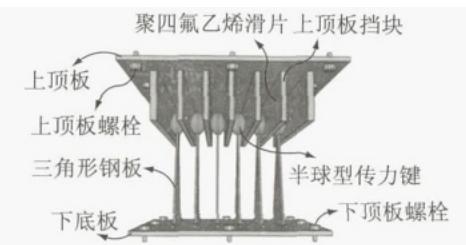
b 钢阻尼器构造
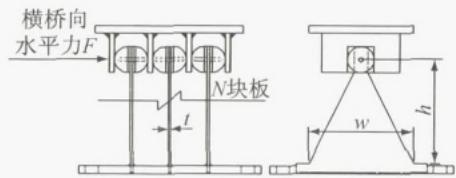
c 钢阻尼器受力图示
图 2 边墩横向减震体系及钢阻尼器构造、受力图示
Fig. 2 Schematic of the proposed isolation system of the bridge outer pier and the hysteretic steel damper
2.2 钢阻尼器参数的确定
本着经济、实用、美观的原则,以钢阻尼器的用钢量 V = 0.5N h w t 取得最小值作为优化控制目标,其控制参数包括三角形钢板数 N 和单块三角形板的几何尺寸(高 h ,宽 w ,厚 t ,见图 2c),而这些参数又决定了钢阻尼器的屈服强度和位移能力。首先,各三角形钢板之间应保持一定间距(一般不小于 5t ),以保证上顶板钢挡块不与三角形钢板发生碰撞,进而可根据边墩、盖梁或系梁顶部的有限空间确定三角形钢板的最大尺寸 (h_{\mathrm{m}},w_{\mathrm{m}}) 与最大数目 N_{\mathrm{m}} 。然后,钢阻尼器的屈服强度 F_{\mathrm{y}} 应不小于配合使用的滑动支座在桥梁正常使用功能状态下的剪切销强度 F_{s} 以保证钢阻尼器在地震到来时的功能完整性,即满足从弹性到塑性的受力过程;同时,钢阻尼器的屈服强度应不大于下部结构所能承受的水平荷载限值 F_{\mathrm{b}} 。在水平荷载下,钢阻尼器的设计位移能力 \Delta_{u} 应不大于理论位移能力 \delta_{u}18。
式中, \delta_{\mathrm{y}} 为三角形钢板的理论屈服位移。综上可根据如下约束函数组(7)得到用钢量函数取得最小值的参数最优解19。
根据上述用钢量优化控制函数和式(6)—(7)所示方法,获得单块三角形板尺寸 (h = 0.55\mathrm{m},w = 0.60\mathrm{m},t = 0.03\mathrm{m}) ,出于安装方便的考虑,以 N= 10 块板为一组。该边墩减震体系记为 T-I-D,各边墩布置钢阻尼器,并与滑动支座配合使用,见图 1b。P7、P16 分别布置两组,P10、P13 分别布置 4 组(两组用于水上引桥,两组用于主桥 )。水上引桥中墩布置了双曲面球型减震钢支座以减小中墩及其基础的地震反应。此外, 为考察所提出的边墩横向减震体系的位移控制能力, 移除 T-I-D 体系中的钢阻尼器, 即边墩仅采用滑动支座, 记为 T-I 体系, 见图 1c。
2.3 全桥数值模型
2.3.1 梁、拱、墩柱及基础的模拟
由于主桥与水上引桥共用桥墩 P10、P13,水上引桥与岸上引桥共用桥墩 P7、P16,地震反应耦联性较大,因此以一联岸上引桥为边界联,采用 SAP200020建立了三维有限元模型,如图 3 所示,上部结构的主梁、钢拱肋(包括风撑)和钢桁架以弹性梁单元模拟,主拱吊杆、水平系杆以弹性桁架单元模拟,桥面板以弹性板单元模拟。下部结构的桥墩、承台以弹性梁单元模拟,基础以“六弹簧”模拟,弹簧刚度由“m 法”确定21。
2.3.2 钢阻尼器与支座的模拟
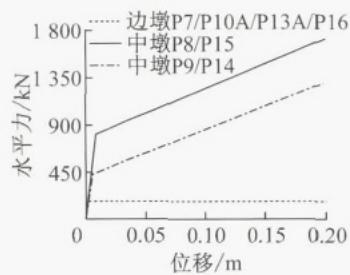
钢阻尼器与支座均采用 Plastic-Wen 单元20模拟。如图 3b 所示,钢阻尼器以双线性本构模拟,一组钢阻尼器的屈服强度为 750\mathrm{kN} ,屈服位移为 0.024m,屈服后刚度为 1560\mathrm{kN}\cdot \mathrm{m}^{-1} ,位移能力保守地取为 0.2\mathrm{m} 。边墩和主桥中墩的滑动型钢支座本构为理想弹塑性,摩擦系数为 0.02,屈服位移取 0.002m;水上引桥中墩的双曲面球型钢支座以双线性本构模拟,考虑屈服后刚度,P8、P15 摩擦系数为 0.04,P9、P14 摩擦系数为 0.02,屈服位移均取 0.002\mathrm{m} 。值得一提的是,由图 3c、3d 可知,边墩的支座恒载反力明显小于中墩。
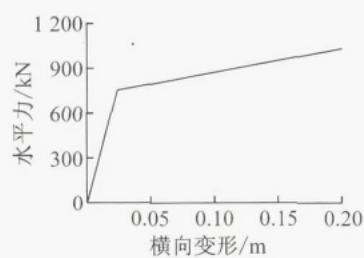
b 横向钢阻尼器力学本构
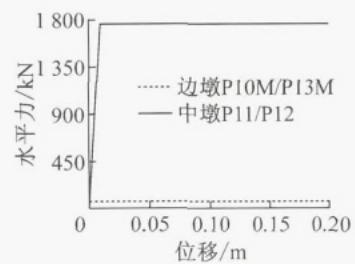
c 主桥滑动支座横向力学本构
a 全桥三维有限元模型(单位:mm)
d 水上引桥支座横向力学本构
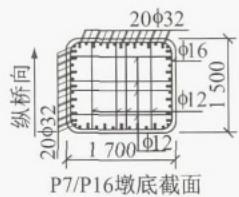
图 3T-I-D 体系全桥三维有限元模型及钢阻尼器、支座的力学本构
3 地震易损性及减震效果分析
3.1 地震波及地震动强度的选择
以该桥址的设计反应谱为目标,从太平洋地震中心(PEER)强震记录库22选取与该场地类型相同的 36 条实测地震波,其对应加速度反应谱的均值与目标反应谱的比较见图 4。
常用的地震动强度参数 (I_{\mathrm{M}}) 包括峰值加速度 (PGA,以 P_{\mathrm{GA}} 表示 ),峰值速度(PGV,以 P_{\mathrm{GV}} 表示),基本周期对应的谱加速度值 (S_{\mathrm{a}}) 等23,24。不同的地震动强度参数对概率地震需求模型及构件地震易损性曲线的建立有较大的影响24,因此,选择合理的地震动强度参数至关重要。由于 PGA 是表征地震波的高频量25,不适用于基本周期较长的桥梁减震体系,而 S_{\mathrm{a}} 不适用于分析比较不同基本周期的桥梁体系中各构件的地震易损性。同时,以往研究26指出,相比于 PGA,PGV 对于概率地震需求模型的建立具有更高的计算效率,即仅需较少的地震输入就可获得拟合度较高的构件地震反应值与 I_{\mathrm{M}} 的对数线性关系。因此,本文选取 PGV 作为地震动强度参数对实例桥梁边墩的不同横向体系进行地震易损性分析。
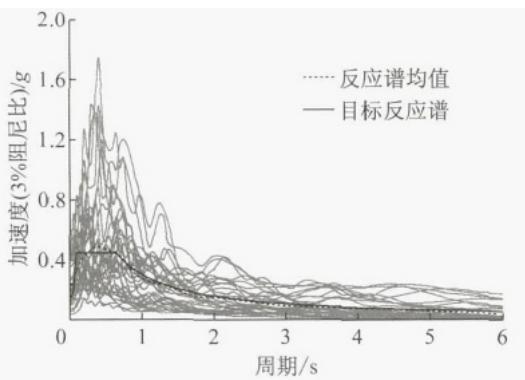
Fig. 3 Numerical model schematic of the T-I-D system and mechanical constitutive of the hysteretic damper and bearings
图 4 所选地震波的加速度反应谱
Fig. 4 Acceleration spectra of selected ground motions
3.2 概率地震需求模型的建立
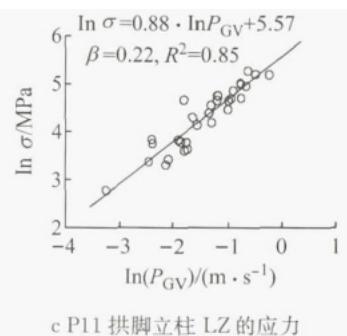
以边墩支座位移,边墩墩底弯矩以及主桥主墩处拱脚立柱(图 3a 中的‘LZ’)的应力为工程需求参数(EDP,以 E_{\mathrm{DP}} 表示)。以 36 条地震波作为输入,通过非线性时程分析得到各 EDP 的地震需求 S_{\mathrm{Di}} 。图 5 代表性地给出了 T-I-D 体系中主桥边墩处支座 P10M 位移 (\delta) 、P10 墩底弯矩 (M) 以及 P11 拱脚立柱 LZ 应力 (\sigma) 的概率地震需求模型。图中 R^2 表示线性拟合相关性,该值越大说明拟合程度越好。图 5a,5b,5c 中, E_{\mathrm{DP}} 分别为 \delta, M 和应力 \sigma 。
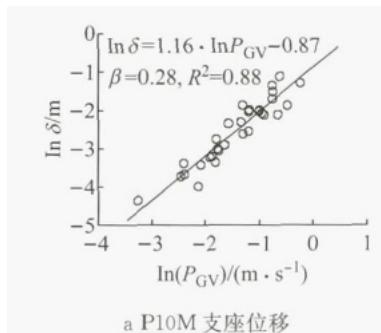
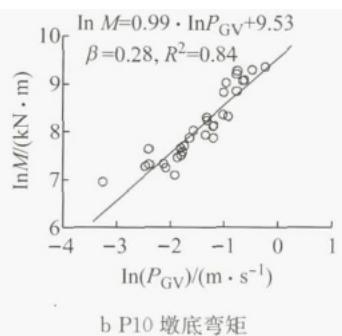
图 5 T-I-D 体系下不同构件的概率地震需求模型
Fig. 5 PSDMs for different components of the bridge with T-I-D system
3.3 损伤指标的确定
3.3.1 边墩支座损伤指标
以滑动支座的横向位移 D_{\mathrm{B}} 为损伤评价指标,图 6 为 T-I-D 体系主桥边墩上滑动支座的潜在损伤图示。表 1 给出了滑动支座各级损伤状态及量化判断标准。根据实例桥梁的具体构造,并参考以往研究23,24,表 2 列出了各级损伤界限的指标值。表中,D_0,D_1,D_2,D_3 分别表示各级损伤状态的临界值。
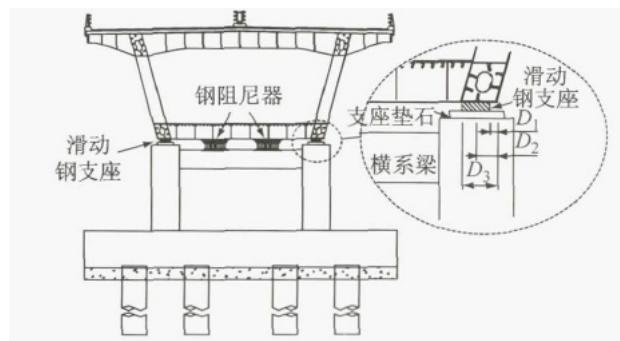
图 6 边墩支座损伤指标定义
Fig. 6 Damage index schematic of bearings at outer piers
3.3.2 边墩墩底、拱脚立柱损伤指标
由于有限元模型的墩柱及上部结构均采用弹性单元,故仅设定一个轻微损伤指标。采用截面分析软件 XTRACT27建立墩底纤维截面,取 C40 混凝土、HRB400 钢筋强度标准值,获得恒载轴力下墩底截面纵向主筋首次屈服时对应的截面弯矩,作为轻微损伤指标。对于拱脚立柱 LZ,以截面最大应力达到所用钢材的理论屈服强度为轻微损伤指标,见表 3。
表 1 边墩支座各级损伤状态划分及判断标准
Tab. 1 Damage index definition of bearings at outer piers
| 状态 | 量化判断标准 | 损伤描述 |
|---|---|---|
| 无损伤 | DB <= D0 | 震后仍处于正常使用滑动范围,剪力销未剪短,仍属于T-R体系 |
| 轻微损伤 | D0 < DB <= D1 | 震后可能产生一定残余位移,但始终与上部结构全截面接触 |
| 中等损伤 | D1 < DB <= D2 | 震后处于轻微脱空状态,但大部分面积尚与梁底保持接触 |
| 严重损伤 | D2 < DB <= D3 | 震后处于半脱空状态,与梁底接触面积小于支座面积的一半 |
| 支座落座 | DB > D3 | 震后与上部结构完全脱空,梁体滑落至垫石或桥墩甚至横系梁上 |
表 2 边墩支座各级损伤指标值
Tab. 2 Damage index of bearings at outer pier
| 损伤状态 | 损伤状态界限 | 界限指标值/mm |
|---|---|---|
| 轻微损伤 | D0 | 50 |
| 中等损伤 | D1 | 150 |
| 严重损伤 | D2 | 200 |
| 支座落座 | D3 | 300 |
3.4 易损性曲线的建立
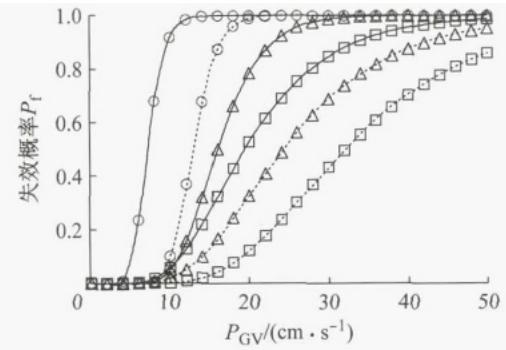
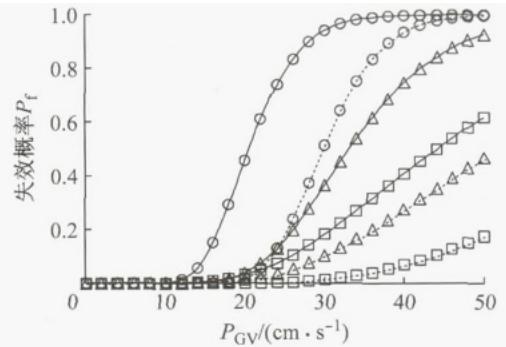
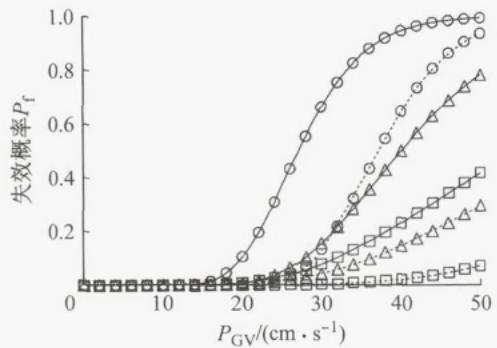
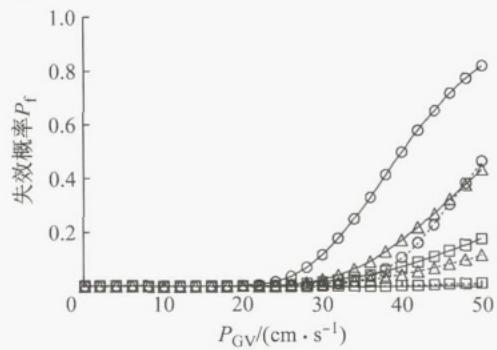
图 7 给出了不同损伤状态下 T-I-D 与 T-I 体系边墩支座的地震易损性曲线。考虑到结构对称性, 仅列出左水上引桥边墩支座 P7、P10A 和主桥边墩支座 P13M 的易损性曲线。图 8 给出了 T-I-D 体系和 T-R 体系边墩墩底截面的易损性曲线,以 P7、P10 为代表。图 9 为不同体系下拱脚立柱 LZ 的地震易损性曲线。
a 轻微损伤
b 中等损伤
c 严重损伤
d 支座落座
图 7 不同损伤状态下 T-I-D 与 T-I 体系下边墩支座地震易损性曲线的比较
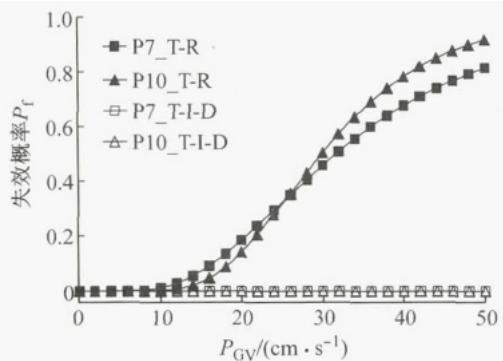
图 8 T-R 与 T-I-D 体系下边墩墩底的易损性曲线
Fig. 8 Fragility curve of the outer pier bottom
表 3 边墩墩底和拱脚立柱的损伤指标值
Tab. 3 Damage index of bearings at outer pier
| EDP | |||
|---|---|---|---|
| P10, P13 墩底弯矩 | P7, P16 墩底弯矩 | LZ 应力 | |
| 损伤指标值 | 50 MN·m | 16 MN·m | 370 MPa |
3.5 减震效果分析
对于支座的损伤,由图 7 可知,所提出的边墩横向减震体系(T-I-D 体系)比 T-I 体系具有更低的失效概率, 即 T-I-D 体系的位移控制效果显著。对于下部结构, 图 8 显示了 T-I-D 体系起到了明显的隔震作用, 显著提高了墩柱在地震中免受损伤的可能性。对于上部结构的损伤, 由图 9 可知,T-I-D 体系下, 拱脚立柱 LZ 的地震易损性显著降低, 原因在于:① 减震体系 (T-I-D、T-I) 比横向约束体系 (T-R) 具有更大的横向基本周期, 地震反应相应更小;② 与 T-I 体系相比,T-I-D 体系有效控制了边墩的横向位移, 进而减小了拱肋立柱 LZ 的地震反应。
图 10 给出了 T-R 和 T-I-D 体系下边墩 P10 在实际地震记录 Northridge 波 ((P_{\mathrm{GA}} = 0.41g, P_{\mathrm{GV}} = 50 cm·s⁻¹,USC90003 测站 )) 作用下的弯矩时程曲线,在 T-R 体系下,P10 墩底截面弯矩已超过屈服弯矩,而在 T-I-D 体系下,P10 墩底弯矩时程值始终较小,保持弹性状态。说明 T-I-D 体系对墩柱起到明显保护作用。图 11 给出了在该地震波下 T-I-D 体系中主桥边墩上钢阻尼器和配合使用的滑动支座 P10M 的力 - 位移关系的比较,可见钢阻尼器发挥了显著的耗能作用,总体而言,以滞回型钢阻尼器和滑动支座配合使用的桥梁边墩减震体系显著提高了边墩的抗震性能。
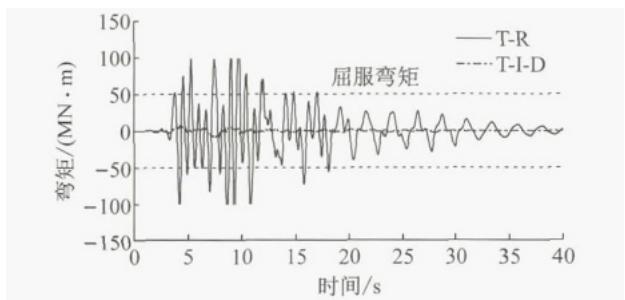
图 10 T-R 与 T-I-D 体系下边墩 P10 墩底弯矩的时程曲线
Fig. 10 Time history of bending moment at the outer pier P10 bottom between the T-R and T-I-D system
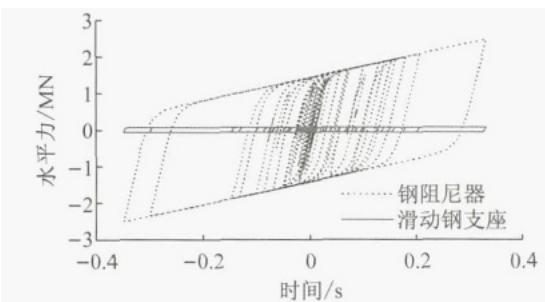
图 11 T-I-D 体系支座 P10M 与钢阻尼器力 - 位移关系比较
Fig. 11 Comparison on the hysteretic property between P10M bearing and the damper in T-I-D system
4 结语
本文针对大跨度桥梁边墩的恒载轴力较小,摩擦型减震支座的耗能作用无法充分发挥的问题,提出了一种以滞回型钢阻尼器和滑动支座配合使用的大跨度桥梁边墩横向减震体系,并基于地震易损性分析方法,以一座大跨度钢桁架拱桥为例,从支座变形、墩柱底弯矩和拱脚立柱应力三个关键工程参量出发,论证了所提出的边墩横向减震体系的合理性。该边墩横向减震体系可用于其他类型大跨度桥梁边墩的抗震设计。
参考文献:
梁智垚, 李建中. 大跨度公铁两用斜拉桥阻尼器参数研究 [J]. 同济大学学报: 自然科学版, 2007, 35(6): 728.
LIANG Zhiyao, LI Jianzhong. Research on damper parameters of long-span rail-cum-road cable-stayed bridge[J]. Journal of Tongji University: Natural Science, 2007, 35(6): 728. ↩Beck J, Skinner R. The seismic response of a reinforced concrete bridge pier designed to step [J]. Earthquake Engineering & Structural Dynamics, 1973, 2(4): 343. ↩
Roussis P, Constantinou M, Erdik M, et al. Assessment of performance of seismic isolation system of Bolu Viaduct[J]. Journal of Bridge Engineering, 2003, 8(4): 182. ↩
周云. 金属耗能减震结构设计 [M]. 武汉:武汉理工大学出版社,2006.
ZHOU Yun. Energy dissipation and isolation design of metal structures [M]. Wuhan: Wuhan University of Technology Press, 2006. ↩潘晋,吴成亮,全强,等. E 型钢阻尼器数值仿真及试验研究 [J]. 振动与冲击,2009,28(7):192.
PAN Jin, WU Chengliang, TONG Qiang, et al. Simulation and experimental study of E shape steel damper[J]. Journal of Vibration and Shock, 2009, 28(7):192. ↩李鹏飞,袁泉,郭猛,等. 普通强度钢耗能器滞回性能的试验研究 [J]. 华南理工大学学报:自然科学版,2011,39(6):148.
LI Pengfei, YUAN Quan, GUO Meng, et al. Experimental Investigation into Hysteresic Performance of Normal-Strength Steel Dampers [J]. Journal of South China University of Technology: Natural Science Edition, 2011, 39(6): 148. ↩王君杰,王志强,章小檀,等.可滑移柱形软钢阻尼装置及其在桥梁上的应用 [P]. 中国:CN200810204146.2,2010-06-23.
WANG Junjie, WANG Zhiqiang, ZHANG Xiaotan, et al. Column-shaped sliderable soft steel damper and its application on bridges[P]. China: CN200810204146.2, 2010-06-23. ↩高峰利. 新型金属阻尼器的减振机理及其在桥梁抗震中的应用 [D]. 长沙:湖南大学,2008.
GAO Fengli. The research on damping mechanism of a new type steel damper and its function in bridge anti-seismic[D]. Changsha: Hunan University, 2008. ↩方圆. 汶川地震典型简支梁桥震害分析及横向限位装置研究 [D]. 上海:同济大学,2012.
FANG Yuan. Research on typical damage of simple supported beam bridge during Wenchuan Earthquake and transverse resistant device[D]. Shanghai: Tongji University, 2012. ↩Casciati F, Cimellaro G, Domaneschi M. Seismic reliability of a cable-stayed bridge retrofitted with hysteretic devices [J]. Computers & Structures, 2008, 86(17-18): 1769. ↩
Padgett J, Desroches R. Methodology for the development of analytical fragility curves for retrofitted bridges[J]. Earthquake Engineering & Structural Dynamics, 2008, 37(4): 1157. ↩
Padgett J, DesRoches R. Retrofitted bridge fragility analysis for typical classes of multispan bridges [J]. Earthquake Spectra, 2009, 25(1): 117. ↩
Zhang J, Huo Y. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method[J]. Engineering Structures, 2009, 31(8): 1648. ↩
Baker J, Cornell C. Vector-valued ground motion intensity measures for probabilistic seismic demand analysis [R]. Berkeley: Pacific Earthquake Engineering Research Center, 2006. ↩ ↩
Billah M, Alam S. Seismic fragility assessment of highway bridges: a state-of-the-art review [J]. Structure and Infrastructure Engineering, 2015, 11(6): 804. ↩ ↩
中华人民共和国交通运输部. JTG/T B02-01—2008 公路桥梁抗震设计细则 [S]. 北京:人民交通出版社,2008. The Ministry of Transport of the People's Republic of China. JTG/TB 02-01—2008 Code for seismic design of urban bridges [S]. Beijing: China Communications Press, 2008. ↩
沈星,倪晓博,叶爱君. 桥梁新型横向金属阻尼器研究 [J]. 振动与冲击,2014,33(21):96. SHEN Xing,Ni Xiaobo,Ye Aijun. Research on metallic damper for bridge in transverse direction [J]. Journal of Vibration and Shock,2014,33(21):96. ↩
Skinney R I, Tyler R, Heine A, et al. Hysteresis Dampers for the Protection of Structures from Earthquakes[J]. Bulletin of New Zealand National Society for Earthquake Engineering. 1980, 13(1): 22. ↩
谢可新,韩立兴,林友联. 最优化方法 [M]. 天津:天津大学出版社,2001.
XIE Kexin, HAN Lixing, LING Youlian. Optimal methodology[M]. Tianjin: Tianjin University Press, 2001. ↩CSI. Sap 2000: V14.1—Static and dynamic finite element analysis of structures[Z]. Berkeley: Computers and Structures, Inc. (CSI), 2009. ↩ ↩
中华人民共和国交通部. JTG D63—2007 公路桥涵地基与基础设计规范 [S]. 北京:人民交通出版社,2007. The Ministry of Transport of the People's Republic of China. JTG D63—2007 Code for design of ground base and foundation of highway bridges and culverts [S]. Beijing: China Communications Press, 2007. ↩
PEER, PEER Ground Motion Database [DB/OL]. [2014-03-26]. http://peer.berkeley.edu/peer-ground_motion_database. ↩
Mackie K, Stojadinovic B. Performance-based seismic bridge design for damage and loss limits states [J]. Earthquake Engineering & Structural Dynamics, 2007, 36(13): 1953. ↩ ↩
Padgett J, Nielson B, DesRoches R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios [J]. Earthquake Engineering & Structural Dynamics, 2008, 37(5): 711. ↩ ↩ ↩
Bazzurro B, Cornell A. Seismic Hazard Analysis of Nonlinear Structures. I: Methodology [J]. Journal of Structural Engineering, 1995, 120(11): 3320. ↩
Wang Z, Padgett J, Duenas-Osorio L. Influence of vertical ground motions on the seismic fragility of a bridge-soil-foundation system[J]. Earthquake Spectra, 2012, 29(3): 937. ↩
XTRACT. Cross-sectional Structural Analysis of Components, Ver. 3.0.8[Z]. Sacramento: Imbsen and Associates II, 2009. ↩