沈星,叶爱君,王晓伟
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:基于 Pushover 分析方法,探索柔性横系梁对双柱式桥墩抗震行为的影响。采用弹塑性纤维单元,建立单柱墩、盖梁双柱墩和柔性横系梁双柱墩模型并进行对比分析,研究横系梁刚度变化对桥墩破坏机理、墩顶位移能力、位移延性系数以及基础受力的影响。结果表明,随着横系梁刚度的增大,墩顶位移延性能力逐渐减小,位移延性系数逐渐增大,桥墩的承载能力逐渐增大,同时提供给基础水平推力能力增大。对于规则桥墩,柔性横系梁双柱墩的墩顶最大塑性位移比单柱墩略小,可按单柱墩位移延性能力计算公式计算其墩顶位移延性能力。
关键词:横系梁;抗震行为;Pushover 分析;塑性位移;位移延性系数
中图分类号:U442.5 文献标志码:A
Seismic Behavior Analysis for Link Beam of Double-column Bent
SHEN Xing, YE Aijun, WANG Xiaowei
(State Key Laboratory for Disaster Reduction of Civil Engineering, Shanghai 200092, China)
Abstract: To explore what seismic behavior effects link beam will have on its double-column bent based on pushover analysis method. The elastic-plastic fiber surface element is applied to the construction of three respective models—single-column bent model, double-column bent model and link beam double-column bent model, to study the capacity difference, displacement ductility factor and force acting on the foundation by changing the stiffness of link beam. The analysis results indicate that with the increasing stiffness of link beam, there will be a decreasing trend of displacement ductility capacity on the top pier, a gradual increase of displacement ductility factor and load-carrying capacity of piers, thus more lateral force capacity will be passed to the foundations. For the regular pier, the maximum plastic displacement on the top pier of the link beam of double-column is slightly smaller than that of single column bent, and its displacement ductility capacity can be calculated as that of single column bent.
Key words: link beam; seismic behavior; Pushover analysis; plastic displacement; displacement ductility factor
桥梁结构的抗震性能评价与桥墩结构所采取的抗震设计策略有关,如对桥墩采用基于性能的设计方法1。随着交通量需求的增加,对桥梁的横向宽度提出更大尺寸要求,而在宽桥中常采用无横向连接的两个单柱墩、柔性横系梁双柱墩以及框架墩等结构形式。柔性横系梁双柱墩通常在一个双柱墩墩顶设置固定支座,另一个墩顶设置滑动支座,为使桥墩结构传递横向水平推力,常采用柔性横系梁来均衡两墩的水平力。袁万城等2通过对单柱墩和框架墩在线性范围内进行动力时程分析来探讨两种结构的抗震性能。Gazetas 等3考虑桩 - 土 - 结构的相互作用下,对柱式桥墩的倒塌做出了机理性分析。目前对柔性横系梁双柱墩抗震性能的研究很少,关于考虑抗震设计对柔性横系梁构造提出明确规定的文献资料也相当不足,因此对柔性横系梁抗震性能的研究十分必要。
本文在 OpenSees 平台下建立墩柱非线性有限元模型,并采用 Pushover 分析方法,比较在共同基础上采用无连接构造的两个单柱墩、两个单柱墩通过柔性横系梁连接以及双柱墩墩顶设置盖梁的框架墩等三种结构形式的破坏机理和抗震性能,及分析柔性横系梁刚度变化对桥墩抗震性能的影响,并得出相关结论,为从事桥梁工程设计师在抗震设计中对桥墩结构形式的选取提供参考。
1 分析方法及材料参数
Pushover 分析方法自 1975 年由 Freeman 等4提出后,经过 20 多年的完善,目前已成为一种成熟的研究结构抗震性能的非线性分析方法。对以低阶振型控制为主、高阶振型对结构影响不明显,且失效模式唯一时,可采用固定荷载模式5,6,7。TatjanaIsakovic8分析比较了单一模态 Pushover 分析、模态 Pushover 分析和增量反应谱分析等方法在单柱墩高架桥横向反应分析中的运用。我国桥梁抗震设计中也逐渐开始采用该方法。该方法可以预测在地震作用下桥梁结构的地震能力。
1.1 荷载模式及加载步骤
当结构以低阶振型控制为主、高阶振型对结构影响不明显且失效模式唯一时,可采用固定荷载模式9,10。基于 OpenSees 平台,对桥墩顶部某一位置施加位移控制的单调递增加载方式,其加载步骤为在桥墩顶部从零开始施加以墩顶产生一定位移为基准的单调递增侧向力,使桥墩经历由弹性—塑性屈服一破坏过程,并比较不同桥墩形式的抗震行为。
1.2 工程背景及模型材料参数
桥墩采用矩形截面,截面尺寸为 1.8\mathrm{m}\times 1\mathrm{m}。墩身采用 C40 混凝土,纵向受拉钢筋采用 HRB335 钢筋,纵向钢筋配筋率为 2.509\%,单柱墩轴压比为 5.89\%,故在墩顶施加竖向荷载 5724.4kN。
墩身单元在 OpenSees 平台中采用弹塑性纤维面来模拟混凝土和钢筋在地震作用下的弹塑性性能。混凝土采用 OpenSees 中的 Concrete01 材料, 不考虑混凝土抗拉强度11。核心混凝土屈服强度和极限强度的计算考虑了纵向钢筋和横向钢筋配筋率、间距以及混凝土标准强度等, 其本构关系如图 1a 所示。钢筋采用 Steel01 材料的双线性本构关系, 其本构关系如图 1b 所示。
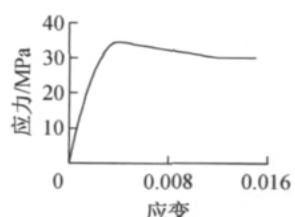
a 约束混凝土
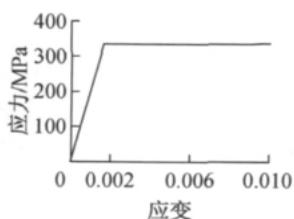
b 钢筋
图 1 材料本构曲线
Fig.1 Material constitutive curves
2 桥墩模型介绍
为探索同一基础之上无系梁双柱墩、柔性横系梁双柱墩和盖梁双柱墩等不同桥墩形式的抗震性能,并考虑实际工程中支座的放置来模拟不同桥墩形式的横向荷载传递模式,因此通过 OpenSees 平台建立以下 4 种模型进行抗震行为比较分析。
2.1 模型一:单柱墩模型
桥墩采用在同一基础之上放置两个不采取任何连接措施的单柱墩形式,这在实际工程中十分常见。这类桥墩通常设计为在一个单柱墩墩顶放置固定支座,另一个墩顶部放置滑动支座。由于滑动支座在地震作用下不传递水平推力,在地震作用下的水平力全部由固定支座来承受,因此该模型可采用单柱墩进行分析,故称为单柱墩模型,墩柱高 10\mathrm{m},具体结构荷载模式以及桥墩墩柱截面配筋如图 2 所示。
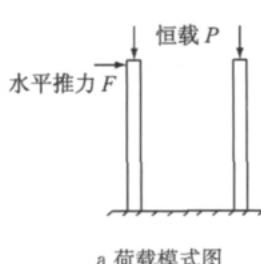
图 2 单柱墩模型示意图
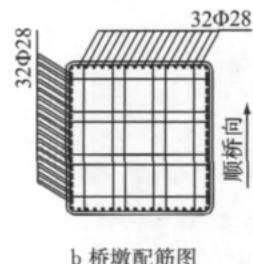
Fig.2 Schematic model of a single-column bent
2.2 模型二:盖梁双柱墩模型
实际工程中,在双柱墩顶设置盖梁,然后在盖梁顶部设置横向支座,可以将上部结构所受到的力均匀地传递给桥墩和基础。为方便与单柱墩在地震作用下的抗震性能比较,本模型采用的双柱墩的墩柱形式与前所述单柱墩相同,盖梁横向长度为 12.5m。为便于与柔性横系梁比较,考虑到通常将盖梁作为能力保护构件,在地震作用下通过在桥墩墩顶和墩底产生塑性铰来耗能,从而使盖梁处于弹性状态12,因此盖梁采用 1\mathrm{m}\times 1\mathrm{m} 的矩形截面,在程序中设定盖梁为弹性单元,并将其弹性模量设置得很大,使其处于弹性阶段。本模型在盖梁质心处施加与单柱墩相同方向的水平推力来模拟实际地震中由上部结构传递的惯性力,并在左、右两墩墩顶施加与单柱墩相同的上部结构恒载。
2.3 模型三:柔性横系梁双柱墩模型
当双柱墩墩柱较高时,要在两个墩柱之间设置横系梁来改善墩柱的受力。为便于与模型二比较,将柔性横系梁设置在墩顶,同时探讨横系梁刚度变化对下部结构抗震行为的影响。
本模型采用的墩柱构造与前述相同,但由于柔性横系梁允许在地震作用下产生屈服或破坏,所以采用纤维单元模拟柔性横系梁在地震作用下由弹性一屈服一破坏过程。为探索横系梁刚度变化对下部结构的影响,此模型中系梁边长分别为 0.6, 1.0, 1.4\mathrm{m} 的矩形截面,即系梁与墩柱相对刚度比分别是:B1 为 0.012,B2 为 0.095,B3 为 0.366。其加载模式与盖梁双柱墩一样。柔性横系梁双柱墩示意图和与墩柱相对刚度比为 B2 时截面配筋图如图 3 所示。
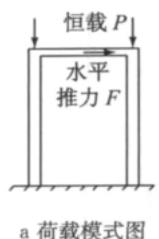
图 3 柔性双柱墩模型示意图
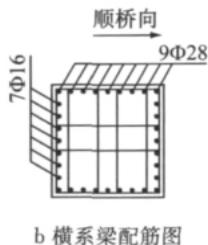
Fig.3 Schematic model of link beam of double-column bent
2.4 模型四:柔性横系梁铰接双柱墩模型
模型三中横系梁与墩柱采用固结连接,在传递水平力的同时还传递了弯矩,本模型中横系梁采用模型三中与墩柱相对刚度比为 0.095(B2)时的截面类型,但是横系梁与墩柱采用铰接,以此与横系梁和墩柱固结时做比较。
3 桥墩破坏机理分析
本节从桥墩结构的破坏过程、双柱墩在控制阶段(屈服阶段和破坏阶段)的内力分析以及对沿墩柱的变形分析来探索不同桥墩结构形式的破坏机理,从而分析比较不同模型在地震作用下的抗震行为。
3.1 桥墩破坏过程
在墩顶每产生 0.00125 \mathrm{~m} 位移可得出对应的水平推力与墩顶位移之间的关系,即 p - y 曲线。通过不同模型的 p - y 曲线比较,可以了解不同形式桥墩由弹性—屈服—破坏过程中水平推力随墩顶位移的变化关系。
图 4 列出 4 种模型的 p - y 曲线,并标记出控制墩首次屈服和最后破坏等控制点。得知单柱墩和双柱墩都是以截面外侧纵向钢筋首次达到极限拉应变标志整个桥墩结构开始进入屈服阶段,最后的破坏形式是以右墩截面外侧核心混凝土被压溃。由图可知 p - y 曲线与横系梁刚度变化有很大关系:即随横系梁刚度的减少,屈服和破坏时的墩顶位移逐渐增大,墩柱承受水平推力能力逐渐减少。由单柱墩模型与墩梁铰接模型对比知:墩梁采取铰接时,横系梁只传递水平力,墩顶位移能力与单柱墩基本一致,而承受水平推力能力是单柱墩的两倍。
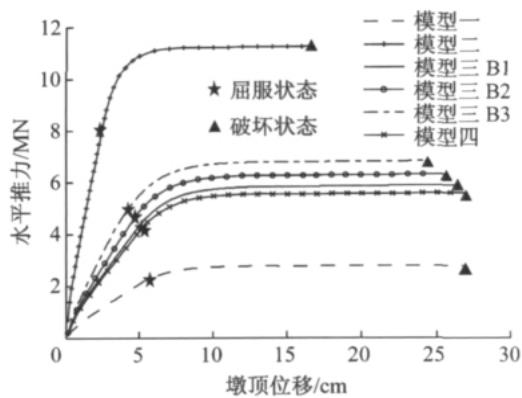
图 4 4 种模型 p - y 曲线比较
Fig.4 Comparison of four models of p - y curves
3.2 双柱墩控制阶段内力分析
双柱墩在地震作用下由于横系梁或盖梁作用,两个墩柱中产生随水平地震力变化的动轴力,而且一个墩柱受动轴拉力,另一个墩柱受动轴压力,使得两个墩柱的破坏机理与单柱墩有很大的区别。而在基于性能的抗震设计方法中需要准确预测桥墩结构的损伤程度,从而来对桥墩结构采用延性设计,因此通过比较不同双柱墩模型在控制阶段的内力分析来探讨双柱墩墩柱的屈服和破坏机理。
柔性横系梁双柱墩的屈服是由右墩控制,而盖梁双柱墩的屈服是由左墩控制。这是因为右墩在推倒过程中承受动轴压力,使其墩柱的刚度增大,从而分配的弯矩也增大。而桥墩结构的屈服是由墩柱底截面最外侧纵向钢筋达到极限拉应变控制。因此桥墩墩柱的屈服要取决于是由弯矩增加引起外侧纵向钢筋拉应力的增加和由动轴压力增加引起外侧纵向钢筋拉应力的减少的权重而决定。通过对表 1 中屈服状态弯矩和轴力分析可知:各双柱墩模型墩底弯矩相差不大,而控制屈服的盖梁双柱墩墩柱轴力却比相应柔性横系梁双柱墩墩柱和墩梁铰接时墩柱的数值大很多,从而导致柔性横系梁双柱墩由右墩控制屈服,盖梁双柱墩由左墩控制屈服,而墩梁铰接双柱墩与单柱墩墩柱受力一样,两个墩柱同时达到屈服状态。
通过对表 1 中破坏状态时内力分析可知:随着横系梁刚度增大,右墩分配的动轴压力增加;控制墩柱在破坏时盖梁双柱墩能够承受弯矩和轴力的能力是最大的,并随着横系梁刚度的减小,其承受弯矩和轴力的能力也减小。结合 p - y 曲线的墩顶破坏位移可知:随横系梁刚度增大,桥墩用墩顶位移能力的减少来获得其弯矩和轴力的承载能力的增加。墩顶的位移减小表示墩底的转角减少, 从而使受压区核心混凝土纤维相对密实, 有效受压面积增大, 从而增大其桥墩承载能力。
表 1 双柱墩控制状态墩底轴力和弯矩比较
Tab. 1 Comparison of the bottom pier from the aspects of axial force and moment of critical statement for double-column bent
| 控制状态 | 内力 | 模型二 | 模型三 B1 | 模型三 B2 | 模型三 B3 | 模型四 |
|---|---|---|---|---|---|---|
| 屈服 | 弯矩/(kN·m) | 21 956.5 | 21 530.8 | 21 594.4 | 21 759.8 | 21 187.3 |
| 轴力/kN | -9 860.2 | -6 658.8 | -7 087.8 | -7 633.1 | -6 628.6 | |
| 破坏 | 弯矩/(kN·m) | 30 919.1 | 28 004.6 | 28 302.8 | 28 673.2 | 27 882.6 |
| 轴力/kN | -11 096.5 | -6 767.8 | -7 197.2 | -7 745.4 | -6 628.6 |
注:轴力负值表示承受轴压力
3.3 变形曲线分析
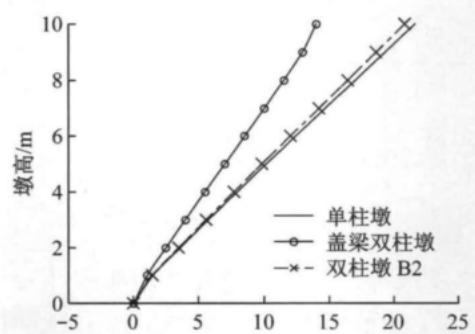
由于不同柔性横系梁双柱墩模型的变化区别不大,因此以柔性横系梁双柱墩 B2 为例,与单柱墩和盖梁双柱墩比较其沿控制墩柱的位移分布,以此比较位移延性能力。
图 5 中列出了柔性横系梁双柱墩 B2、单柱墩及盖梁双柱墩的位移分布图来探索双柱墩和单柱墩墩顶屈服位移和墩顶塑性位移的关系。图 5a 中显示屈服时三个模型沿墩身的变形曲线与弹性时基本一致, 柔性横系梁双柱墩墩顶屈服位移偏向于单柱墩, 图 5b 中显示双柱墩沿墩高的塑性位移分布可以看成绕塑性铰区内一点的转动。
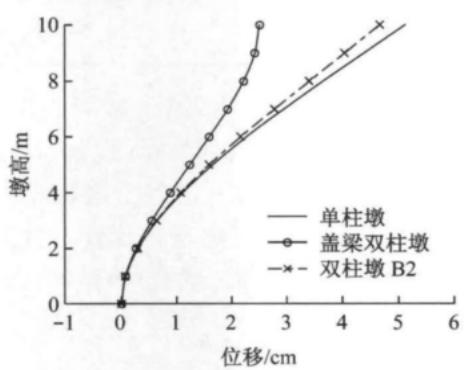
a 屈服位移
图 5 控制阶段位移分布图
Fig. 5 Displacement distribution of critical stages
位移 /cm
b 塑性位移
三个模型墩顶塑性位移可为绕塑性铰内一点的转动。为了便于计算墩顶最大塑性位移,引入“等效塑性铰长度”概念,即在墩底附近存在一个长度为 L_{\mathrm{p}} 的等效塑性曲率段,在该段长度内,截面的塑性曲率等于墩底截面的最大塑性曲率 \varPhi_{\mathrm{p}},塑性曲率 \varPhi_{\mathrm{p}} 即为沿墩高 h 任一点的破坏状态和屈服状态曲率之差。由等效塑性铰长度 L_{\mathrm{p}} 计算的墩顶最大塑性位移,与实际曲率分布计算的结果相等。
利用曲率的积分公式可求出以上三个模型的塑性转角 \theta_{\mathrm{p}},即:
式(1)表示沿墩身对产生塑性铰有贡献的塑性位移高度范围内(从墩底到反弯点的距离内)进行塑性曲率积分。
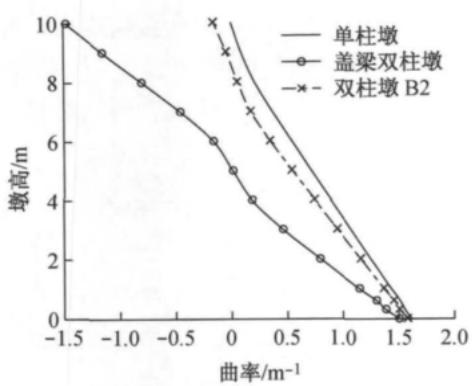
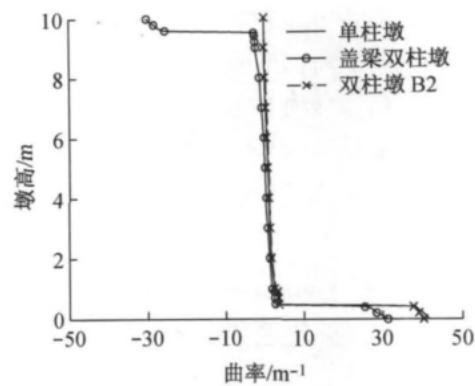
屈服曲率和破坏曲率沿墩高的分布见图 6,等效塑性铰长度计算公式可表达为
由式(2)可知,等效塑性铰长度与墩底极限曲率 \Phi_{\mathrm{u}}、墩底屈服曲率 \Phi_{\mathrm{y}} 和塑性转角 \theta_{\mathrm{p}} 有关。
由表 2 知:盖梁双柱墩在墩底产生的塑性转角最小,柔性横系梁双柱墩比单柱墩略小。盖梁双柱墩在墩顶和墩底都形成了塑性铰,但是墩顶的塑性铰对墩顶位移能力的影响不敏感,故曲率积分沿反弯点到墩底的距离来得到双柱墩的塑性转角。根据墩
a 屈服曲率
图 6 控制阶段曲率分布图
Fig. 6 Curvatures distribution of critical stages
b 破坏曲率
顶最大塑性位移近似等于塑性转角与墩高的乘积,可验证三种模型的墩顶塑性位移都是绕塑性铰区内一点的转动,且大小与图 5b 中各模型一致。考虑到柔性横系梁相对于桥墩的刚度比较小,其产生的墩底塑性转角与单柱墩相差不大,最后表现出的墩顶最大塑性位移比单柱墩略小。由此可对柔性横系梁双柱墩用单柱墩位移能力计算公式进行简化抗震能力验算。
表 2 塑性铰长度和等效塑性铰长度比较
Tab. 2 Comparison of the length of plastic hinge and equivalent plastic hinge
| 名称 | 屈服曲率 \Phi\mathrm{y}/\mathrm{m}^{-1} | 极限曲率 \Phi\mathrm{u}/\mathrm{m}^{-1} | 塑性转角 \theta\mathrm{p}/\mathrm{rad} | 等效塑性铰长度 \mathrm{Lp}/\mathrm{m} |
|---|---|---|---|---|
| 单柱墩 | 0.00162 | 0.04151 | 0.02113 | 0.52963 |
| 盖梁双柱墩 | 0.00150 | 0.03128 | 0.01379 | 0.46294 |
| 刚度比B2 | 0.00158 | 0.04035 | 0.02015 | 0.51981 |
4 抗震性能分析
4.1 延性比较
在初始强度没有明显退化情况下的非弹性变形能力称之为延性。在利用延性概念设计结构抗震时,常采用的延性指标为曲率延性系数与位移延性系数。单柱墩的曲率延性系数与位移延性系数的对应关系如下:
式中: \mu_{\Delta},\mu_{\Phi} 表示位移延性系数和曲率延性系数; \Delta_{\mathrm{y}}, \Delta_{\mathrm{p}} 表示墩顶屈服位移和破坏位移; l_{\mathrm{p}},l 表示塑性铰长度和墩高。表 3 中列出以上各模型在屈服和破坏时的墩顶位移,并根据位移延性系数是构件的极限位移 \Delta_{\mathrm{u}} 与屈服位移 \Delta_{\mathrm{y}} 的比值得到,即:
通过式(4)计算相应的位移延性系数,比较分析横系梁刚度比的变化对结构延性的影响。
表 3 中说明随着横系梁刚度增大,屈服位移和破坏位移都逐渐减少,位移延性系数逐渐增大。墩梁铰接双柱墩位移延性系数与单柱墩基本相同。
表 3 位移延性系数比较
Tab. 3 Comparison of the displacement ductility factor
| 模型一 | 模型二 | 模型三 B1 | 模型三 B2 | 模型三 B3 | 模型四 | |
|---|---|---|---|---|---|---|
| 屈服位移/m | 0.051 3 | 0.025 0 | 0.049 6 | 0.046 7 | 0.042 8 | 0.050 7 |
| 破坏位移/m | 0.267 5 | 0.165 0 | 0.261 8 | 0.255 0 | 0.243 7 | 0.268 0 |
| 位移延性系数 | 5.219 5 | 6.600 0 | 5.277 5 | 5.464 2 | 5.698 8 | 5.287 9 |
在罕遇地震作用下,桥墩越早屈服,对于整体结构的耗能越有利。所以柔性横系梁刚度越大,桥墩的延性越好,对于桥墩抗震越有利。
4.2 基于能力设计方法对基础受力影响分析
在桥梁抗震设计中,对桥墩采用基于延性的抗震设计方法,利用其进入塑性后产生塑性变形来消耗地震能量,以减少地震力对其他构件的破坏。而基础因埋置于地底,损坏后难以发现和修复,而且基础的损害对整个桥梁结构将产生致命的损伤,故对基础应采用能力保护的设计方法。即要求对基础的设计强度比墩柱大,且基础能够承受的内力要比桥墩大。
由于所有桥墩结构都是在一个共有基础之上,故基础在破坏时承受的轴力都是桥梁自身结构的恒载。故表 4 中给出不同模型桥墩在破坏时能够传递给基础的最大弯矩和水平推力能力,以此来研究各模型对基础采用基于能力设计方法时的受力影响。
由表 4 可知,桥墩结构屈服之后,双柱墩墩底能够传递给基础的弯矩能力相差不大。双柱墩传递给基础水平推力能力随着横系梁的刚度增大,同时在共有基础之上放置两个无横向连接构造的单柱墩形式传递给基础水平推力和弯矩能力最小。墩梁铰接时能够传递给基础的弯矩和水平推力能力是单柱墩的两倍,但是比柔性横系梁双柱墩和盖梁双柱墩小。
表 4 基础的受力比较
Tab. 4 Comparison of forces in foundation
| 内力 | 模型一 | 模型二 | 模型三 B1 | 模型三 B2 | 模型三 B3 | 模型四 |
|---|---|---|---|---|---|---|
| 水平推力/kN | 2 779.38 | 11 250.8 | 5 873.99 | 6 299.83 | 6 815.59 | 5 576.23 |
| 弯矩/(kN·m) | 27 793.8 | 56 659.9 | 55 710.2 | 55 890.1 | 56 129.5 | 55 762.2 |
下部结构在地震作用下,由于基础修复的困难大。下部结构的抗震设计往往由基础来控制,所以在抗震设计中要求桥墩能够提供给基础的水平推力能力越小越好。故单柱墩与墩梁铰接模型对基础抗震设计更有利。
5 结论
综上分析可知:
(1)柔性横系梁的位移延性能力验算可参照单柱墩位移延性能力计算公式进行简化计算。
(2)盖梁双柱墩的位移延性系数最大,单柱墩的位移延性系数最小,柔性横系梁双柱墩随着系梁刚度的变化介于两者之间。因此,对于桥墩的延性抗震性能,盖梁双柱墩最好。
(3)桥墩结构屈服之后,随着横系梁刚度增大,延性桥墩能够提供给基础的水平推力能力增大。因此,对于作为能力保护构件的基础,单柱墩能够传递下来的内力能力最小,对基础抗震设计更有利。
(4)在延性抗震设计中,单柱墩和盖梁双柱墩各有不足,而柔性横系梁双柱墩是一种较好的折中方案。同时,在横向两个支座不对称设置的情况下,可以很好地均衡两个墩柱之间的水平力和弯矩。
(5)当基础的受力控制抗震设计时,可以采用柔性横系梁与墩柱铰接的方式,这样延性桥墩能够提供给基础的水平推力能力最小,而且能够均衡两个墩柱之间的水平推力,对基础抗震设计有利。
参考文献:
Priestley MJN. Performance based seismic design [J]. Engineering Structures, 2000, 25(14): 1803. ↩
袁万城,胡勃,范立础. 柱式桥墩横向抗震性能及评价 [J]. 同济大学学报:自然科学版,1996,21(6):601. YUAN Wancheng, HU Bo, FAN Lichu. Aseismic capacity and assessment of column piers[J]. Journal of Tongji University: Natural Science, 1996, 21(6): 601. ↩
Gazetas G, Mylonakis G. Seismic soil-structure interaction: new evidence and emerging issues[C]// Proceedings of 3rd Conference Geotechnical Earthquake Engineering and Soil Dynamics. Seattle:ASCE, 1998:434-444. ↩
Freeman SA, Nicoletti JP, Tyrell JV. Evaluations of existing buildings for seismic risk-A case study of Puget Sound Naval Shipyard, Bremerton, Washington [C]//Proceedings of 1st United States National Conference on Earthquake Engineering. Oakland: [s.n.], 1975: 113-122. ↩
Kilar V, Fajfar P. Simplified pushover analysis of building structures [J]. Earthquake Engineering and Structure Dynamics, 1997(26): 233. ↩
Moghadam A S, Tso W K. A pushover procedure for tall buildings[C]//Proceeding of the 12th European Conference on Earthquake Engineering. London: Elsevier Science Ltd, 2002: 395-403. ↩
Chopra A K, Geol R K. A modal pushover analysis procedure for estimating seismic demands for buildings[J]. Earthquake Engineering and Structural Dynamics, 2002, 31: 561. ↩
Isakovic T, Lazaro MP N, Fischinger M, et al. Applicability of pushover methods for the seismic analysis of single-column bent viaducts [J]. Earthquake Engineering and Structural Dynamics, 2008(37): 1185. ↩
Helmut Krawinkler, Seneviratna G D P K. Pros and cons analysis of seismic evaluation of a pushover performance [J]. Engineering Structures, 1998, 20(4-6): 452. ↩
盛光祖,李建中,陈亮.桥梁单墩不同侧向力模式 Pushover 分析方法 [J]. 振动与冲击,2010,29(2):170. SHENGGuangzu,LIJianzhong,CHENLiang.Pushover analysis of different distribute lateral load patterns for seismic assessment of bridge piers[J].Journal of Vibration and Shock,2010,29(2):170. ↩
Chang G A, Mander J B. Seismic energy based fatigue damage analysis of bridge columns: part I—evaluation of seismic capacity[R]. New York: Technical Report NCEER-94-0006, 1994. ↩
Priestley MJ N, Seible F, Calvi C M. Seismic design and retrofit of bridge [M]. New York: Wiley & Sons, 1996. ↩