赫中营,叶爱君
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:针对目前结构非线性分析中最常用的力法非线性梁柱单元模型,从理论上分析出了能消除其计算失真问题的合理单元长度及对应积分点数量。然后基于 OpenSees 有限元程序,使用该理论分析结果建立了一组单墩循环推倒试验的数值分析模型,通过加载点力 - 位移滞回曲线的对比分析和墩底截面曲率滞回曲线的对比分析验证了理论结果的正确性。结果表明:使用力法非线性梁柱单元模型进行结构的非线性数值分析时,其单元长度划分应根据积分点数量确定,确定原则应基于使单元屈服后变形增长的分布长度与塑性铰长度相等进行计算;在实际使用中,可利用等效塑性铰长度计算积分点数量与单元长度的关系,初步确定单元划分的合理长度;在保证单元长度与积分点数量的对应关系前提下,力法非线性单元的积分点数量越多,计算结果越稳定。
关键词:非线性有限元理论;数值模拟;力法非线性梁柱单元;积分点;单元长度
REASONABLE DISCRETE ELEMENT LENGTH OF FORCE-BASED NONLINEAR BEAM-COLUMN ELEMENTS
HE Zhong-ying, YE Ai-jun
(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: Force-based nonlinear beam-column elements are frequently used in structure nonlinear analysis. In this study, the reasonable discrete element length and the corresponding integration point number are derived theoretically to eliminate computational errors. Subsequently, a numerical model is established, using the OpenSees finite element program, for a set of single-pier cyclic pushover tests. The derivation is verified by comparing both the force-displacement hysteresis curves for load point and the section curvature hysteresis curves at the pier bottom. Results show that: the discrete element length should be determined on the basis of the integration point number when force-based nonlinear beam-column elements are used, and the relationship between the discrete element length and the integration point number is to ensure the length of plastic curvature increments in FEM equal to the plastic hinge length in the actual structure. In practice, the equivalent plastic hinge length can be used to pre-calculate the reasonable discrete element length. If the aforementioned relationship is ensured, the more force-based nonlinear beam-column element integration points are employed, the more reliable the results are.
Key words: nonlinear finite element theory; numerical modeling; force-based nonlinear beam-column element; integration point; element length
随着工程抗震科学技术和理论的发展,基于性能的抗震设计方法得到了广泛应用,目前很多抗震设计规范1均允许结构在一定的地震荷载水准下进入非弹性工作状态,并建议使用非线性静力 Pushover 分析或非线性动力分析方法分析结构地震需求和能力。目前常用的梁柱构件的非线性有限元模型主要分为两类:集中塑性模型和分布塑性模型2,后者又分为基于位移法2和力法3的分布塑性模型。基于位移法的模型中,单元位移场被表示成节点位移场的函数,只是真实结构单元位移场的近似,要想得到精确反应很好的近似结果,就需要将一个构件划分为若干个单元;而基于力法的模型中,单元内力场被表示成节点力的函数,是框架结构经典梁理论的确切表达,如果不考虑数值方法引起的误差,其计算结果即应为精确解,一个构件划分为一个单元即可。
分布塑性模型通过纤维模型截面或应力依赖模型截面和非线性材料本构关系实现,能在构件任意位置处形成塑性铰,在结构抗震分析领域最为常用,很多学者也对其进行了分析研究。文献4以结构整体反应为目标,对基于位移和力法的非线性梁柱单元的计算精度和效率进行了对比分析,结果表明,仅增加数值积分点的数目就能使基于力法的非线性单元达到预期计算精度,而基于位移法的非线性单元则不能。文献5针对基于力法的非线性单元,分析讨论了其计算精度问题,结果表明,对于应变强化截面模型,力法非线性单元不存在反应失真问题,对于完全塑性截面模型,力法非线性单元屈服阶段反应对积分点数量非常敏感,并且屈服后截面曲率增长主要集中在节点位置的积分点处,对于应变软化截面模型,力法非线性单元不仅存在和完全塑性截面模型相同的问题,而且其整体力 - 位移反应也对积分点数量非常敏感。为此,文献6对基于力法的非线性梁柱模型进行修正,提出了塑性铰积分模型以消除力法模型的缺点,该方法是在单元两端塑性铰长度范围内使用纤维截面单元,其他区域使用弹性单元,并使用修正的两点 Gauss-Radau 积分方法进行数值积分计算,该模型能以一个单元模拟一个结构构件的非线性力学性能,单元长度较长,通用性较差。文献7基于单墩试验对位移非线性梁柱单元和力法非线性梁柱单元进行了探讨,结果表明,虽然力法非线性单元存在局部失真的缺点,但其计算精度仍高于位移法非线性单元。
由以上分析可知,力法非线性梁柱模型的计算精度和计算效率均高于位移法非线性梁柱模型,但是对于完全塑性截面模型和应变软化截面模型,其自身又存在反应失真的问题,这就使力法非线性梁柱模型的单元长度和积分点数量选择至关重要,而目前对如何选取单元长度和积分点数量才能使力法非线性梁柱模型的计算结果符合客观实际,并无相关研究报道。
本文针对力法非线性梁柱单元模型,首先从计算原理出发,在理论上探讨了该有限元模型的合理单元划分和积分点数量;然后基于一组单墩循环推倒试验数据和数值模拟结果,以加载点力 - 位移滞回曲线和墩底截面的曲率滞回曲线为目标,从数值上验证了该单元划分和积分点数量选择的正确性。所得结论具有普遍适用性,不仅对正确使用力法非线性梁柱单元模型进行钢筋混凝土结构非线性数值计算具有十分重要的意义,还可为最优数值模型的建立提供极大方便。
1 合理单元长度的理论分析
力法非线性梁柱纤维单元模型仍然以 Euler-Bernoulle 经典梁理论为基础,符合平截面假定,并假定扭转反应是线弹性的,且不和轴向以及弯曲反应耦合,因此其控制方程中不包括扭转自由度。力法非线性梁柱纤维单元模型的计算原理8,9如图 1 所示8,计算分 4 个层次:整体结构层次,单元层次,截面层次和材料本构,图中 U(t) 和 P_{\mathrm{r}}(U(t)) 分别为结构层次节点位移向量和抗力向量,P_{\mathrm{f}}(t) 为结构层次外部节点荷载向量,u_{i} 和 p_{i} 分别为整体坐标系下第 i 个单元的节点位移向量和抗力向量,a_{i} 为整体坐标系下将某单元节点位移向量用结构层次中节点位移向量表示的选择矩阵,v 和 q 分别为单元局部坐标系下单元的节点位移向量和抗力向量,e 和 s 分别为截面变形向量和截面抗力向量,s_{\mathrm{p}} 为单元荷载作用下静定体系的截面力向量,b 为用单元节点力表示截面内力的插值函数矩阵,\sigma 和 \varepsilon 分别为截面材料的应力和应变。
从图 1 可看出,力法非线性梁柱单元模型的非线性取决于纤维截面材料的非线性,由材料的非线性本构关系唯一确定,梁柱模型单元本身的非线性则主要来源于内力和变形的插值函数。
图 1 框图③中表达式 \pmb{v} = \int_{0}^{L}\pmb{b}^{\mathrm{T}}\pmb{e}\mathrm{d}x 并不能用于实际有限元计算,使用 Gauss 系列数值积分方法计算 \pmb{v} 可达到较好的效果,其计算表达式:
式中:N_{\mathrm{p}} 为积分点个数;x_{i} 为积分点位置;\omega_{i} 为积分点权值。对于图 1 框图②中所示局部坐标系下的二维结构单元,线性插值函数 \pmb{b} 如下式所示:
由框图③和式 (1) 可看出,力法非线性梁柱单元直接使用数值积分方法计算单元节点位移,单元积分点数量直接决定曲率的分布。再结合图 1 框图③~⑤和文献4,5,6,7的成果可知,由于截面材料的非线性,在屈服后阶段,力法非线性梁柱单元的曲率增长主要集中在节点位置处 ( 即第 1 个或第 N_{\mathrm{p}} 个积分点处 )。
在实际结构中,构件屈服后,截面变形沿构件的分布极其复杂,很难用某一具体函数进行表示,但其屈服后变形增长也主要集中在一定区域内 ( 为便于叙述,将该区域长度定义为塑性铰长度,以 l_{\mathrm{pc}} 表示 ),因此,从理论上来说,应该使数值模型中屈服后变形增长的分布长度与塑性铰长度相等,也就是说,对于力法梁柱单元的合理单元长度应该根据积分点个数和塑性铰长度决定,原则上应使节点位置处积分点截面变形对节点变形的贡献与塑性铰的贡献相等,因此合理的单元长度应该为节点位置处截面对该节点变形贡献 ( 对于框图③中的 \nu_{2} 为 \frac{b_{22}(x_1)\omega_1}{\sum_i[b_{22}(x_i)\omega_i]} ,对于 \nu_{3} 为 \frac{b_{23}(x_{N_{\mathrm{p}}})\omega_{N_{\mathrm{p}}}}{\sum_i[b_{23}(x_i)\omega_i]}) 的倒数与塑性铰长度的乘积。
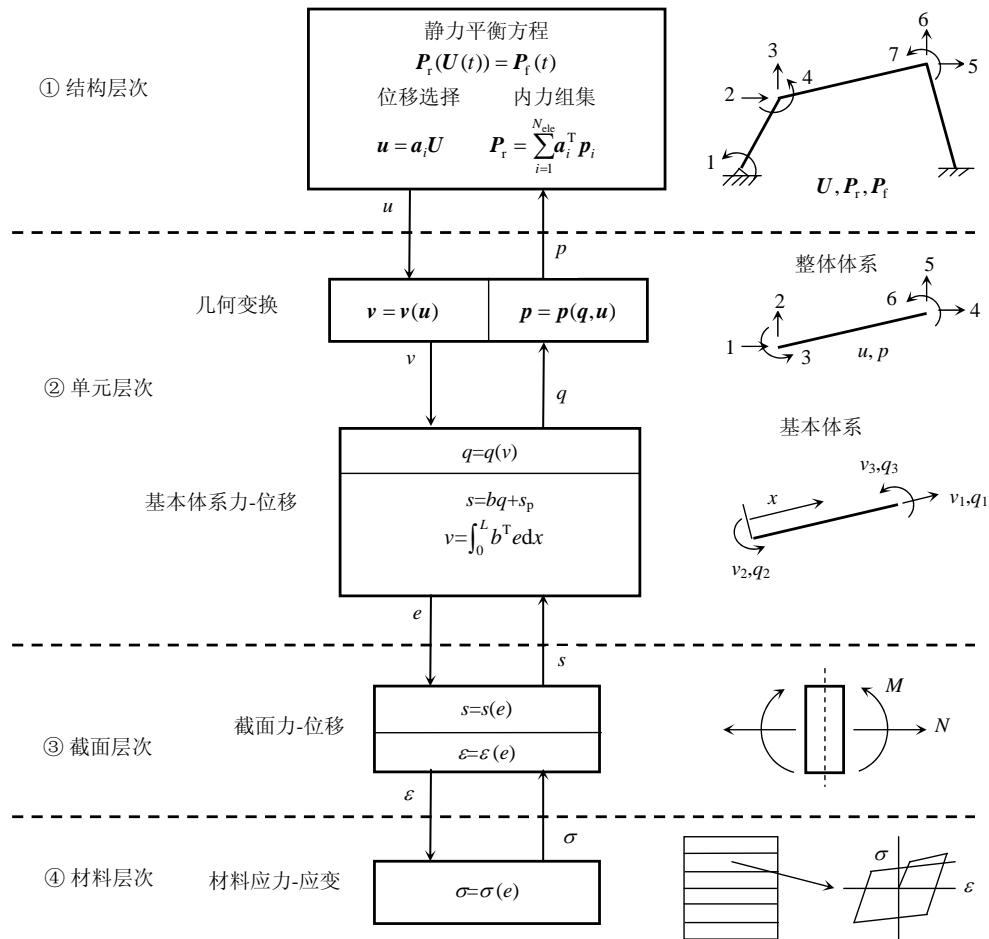
图 1 非线性结构模型计算原理图
Fig.1 Modeling hierarchy for nonlinear structural analysis
对于目前常用的有限元计算程序 (比如 OpenSees),普遍采用 Gauss-Lobatto 积分方法计算 \pmb{\nu} ,表 1 列出了积分点个数为 2~5 个时 Gauss-Lobatto 积分方法中的 x_{i} 值、\omega_{i} 值 (i = 1\sim N_{\mathrm{p}}) ,从而根据式 (1) 和式 (2) 可算出力法非线性梁柱单元各积分点位置处的 b_{22}(x_i)\omega_i ( 对应于框图③中的 \nu_{2},i = 1\sim N_{\mathrm{p}}) 和 b_{23}(x_i)\omega_i ( 对应于框图③中的 \nu_{3},i = 1\sim N_{\mathrm{p}})、节点位置处截面变形对该节点变形的贡献 \frac{b_{22}(x_1)\omega_1}{\sum_i[b_{22}(x_i)\omega_i]} 和 \frac{b_{23}(x_{N_{\mathrm{p}}})\omega_{N_{\mathrm{p}}}}{\sum_i[b_{23}(x_i)\omega_i]} 以及单元的合理长度,一并列于表中。
表 1 Gauss-Lobatto 积分方法中 \omega_{i}、x_{i} 值和单元合理长度
Table 1 \omega_{i}、x_{i} values and reasonable element length using Gauss-Lobatto quadrature rule
| N_{\mathrm{p}} | x_{i} | \omega_{i} | b_{22}(x_{i})\omega_{i} | b_{23}(x_{i})\omega_{i} | \frac{b_{22}(x_1)\omega_1}{\sum_i[b_{22}(x_i)\omega_i]} (\frac{b_{23}(x_{N_{\mathrm{p}}})\omega_{N_{\mathrm{p}}}}{\sum_i[b_{23}(x_i)\omega_i]}) | 单元合理长度 |
|---|---|---|---|---|---|---|
| 2 | 0 | 0.5 | -0.5 | 0 | 1(1) | l_{\mathrm{pc}} |
| L | 0.5 | 0 | 0.5 | |||
| 3 | 0 | 0.16667 | -0.16667 | 0 | 0.3333(0.3333) | 3l_{\mathrm{pc}} |
| 0.5 L | 0.66667 | -0.33333 | 0.33333 | |||
| L | 0.16667 | 0 | 0.16667 | |||
| 4 | 0 | 0.08333 | -0.08333 | 0 | 0.1667(0.1667) | 6l_{\mathrm{pc}} |
| 0.27639 L | 0.41667 | -0.3015 | 0.11516 | |||
| 0.72361 L | 0.41667 | -0.11516 | 0.3015 | |||
| L | 0.08333 | 0 | 0.08333 | |||
| 5 | 0 | 0.05 | -0.05 | 0 | 0.1(0.1) | 10l_{\mathrm{pc}} |
| 0.17267 L | 0.27222 | -0.225221 | 0.04701 | |||
| 0.5 L | 0.35556 | -0.17778 | 0.17778 | |||
| 0.82733 L | 0.27222 | -0.04701 | 0.22522 | |||
| L | 0.05 | 0 | 0.05 |
由于实际结构在屈服后截面变形沿构件分布的复杂性,其塑性铰长度很难确定。为便于分析计算,一般将实际结构中的塑性铰长度用等效塑性铰长度10表示。其计算公式一般为由实验所得的经验公式11,比较常用的为 Paulay 和 Priestley 的推荐公式12,如下式所示:
式中:l_{\mathrm{p}} 为等效塑性铰长度;l 为墩柱反弯点到最大弯矩截面的长度;d_{\mathrm{s}} 和 f_{\mathrm{y}} 分别为纵筋直径和屈服应力。
2 合理单元长度的数值验证
日本东京工业大学川岛试验室 (Kawashimalaboratory of the Tokyo institute of technology) 对钢筋混凝土桥墩进行了大量的拟静力循环荷载试验,这些试验的资料和数据均可以从 http://seismic.cv.titech.ac.jp 网页上得到,其中编号为 TP010~TP013 的 4 个矩形桥墩主要用于研究纵向主筋直径对塑性铰长度的影响,4 个桥墩有效高度均为 1.45\mathrm{m},截面尺寸均为 0.4\mathrm{m} \times 0.4\mathrm{m},材料及其他参数如表 2 所示。
表 2 试件材料参数
Table 2 Material properties in the test
| 试件编号 | 纵筋性能 | 箍筋性能 | 箍筋间距/cm | 混凝土抗压强度f_{\mathrm{c}}^{\prime}/\mathrm{MPa} | 保护层厚度/cm | 轴向荷载/kN | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 型号 | 屈服强度f_{\mathrm{y}}/\mathrm{MPa} | 配筋率/(%) | 型号 | 屈服强度f_{\mathrm{yh}}/\mathrm{MPa} | 配箍率/(%) | |||||
| TP010 | SD295A D10 | 377 | 1.07 | SD295 D6 | 376 | 0.77 | 5 | -21.0 | 4.10 | 160 |
| TP011 | SD295A D13 | 367 | 0.95 | SD295 D6 | 376 | 0.77 | 5 | -20.6 | 4.25 | 160 |
| TP012 | SD295A D16 | 364 | 0.99 | SD295 D6 | 376 | 0.77 | 5 | -20.3 | 4.40 | 160 |
| TP013 | SD345 D13 | 375 | 0.95 | SD295 D6 | 376 | 0.77 | 5 | -21.0 | 4.25 | 160 |
根据式 (3) 可算出 TP010~TP013 的等效塑性铰长度分别为 19.5\mathrm{cm}、21.8\mathrm{cm}、24.3\mathrm{cm} 和 22.1\mathrm{cm}。
本文基于 OpenSees 有限元程序建立 TP010TP013 桥墩的数值分析模型,并根据表 1 所示的积分点数量进行不同单元长度划分,从加载点力 - 位移曲线和墩底截面曲率两个方面,验证其合理性。由于等效塑性铰计算公式只是近似计算,数值模拟时 TP010TP013 的等效塑性铰长度均取为 20\mathrm{cm}。
2.1 有限元模型建立
有限元模型中每根纵向钢筋作为一个纤维单元,采用 ReinforcingSteel 模拟,其骨架曲线如图 2 所示, 钢筋屈服强度 f_{\mathrm{y}} 如表 2 所示, 极限强度 f_{\mathrm{su}} 取 1.52 f_{\mathrm{y}} , 初始弹性模量 E_{\mathrm{s}} 取 f_{\mathrm{y}} / 0.002 , 应变强化切线模量 E_{\mathrm{sh}} 取 0.035, 对于 SD295A 和 SD345 主筋, 初始强化应变 e_{\mathrm{sh}} 分别取 0.005 和 0.01, 极限应力对应的应变 e_{\mathrm{ult}} 分别取 0.15 和 0.20, 采用 Gomes-Appleton 屈曲模型13模拟钢筋的屈曲效应, 采用 Coffin-Manson 损伤模型14考虑钢筋的疲劳和强度退化效应, 屈曲和疲劳强度退化参数如表 3 所示。
箍筋的作用通过核心混凝土效应考虑,每个截面的核心混凝土划分为 576 个纤维单元,保护层混凝土划分为 448 个纤维单元,保护层混凝土和核心混凝土均采用应变软化单元 Concrete01 模拟,不考虑混凝土抗拉能力,保护层混凝土 28 天抗压强度 f_{\mathrm{pc}} 即为表 2 中所列 f_{\mathrm{c}}^{\prime} ,对应的应变取 \varepsilon_{\mathrm{c0}} = -0.002 ,压碎强度 f_{\mathrm{pcu}} 取抗压强度 (f_{\mathrm{pc}}) 的 20\% ,极限应变取 \varepsilon_{\mathrm{u}} = -0.005 。核心混凝土的最大抗压强度及其对应的应变可按照修正的 Kent-Park 模型15计算,压碎强度取最大抗压强度的 20\% ,极限应变也根据文献15推荐的公式计算,计算所得的核心混凝土参数值如表 4 所示,Concrete01 骨架曲线如图 3 所示。
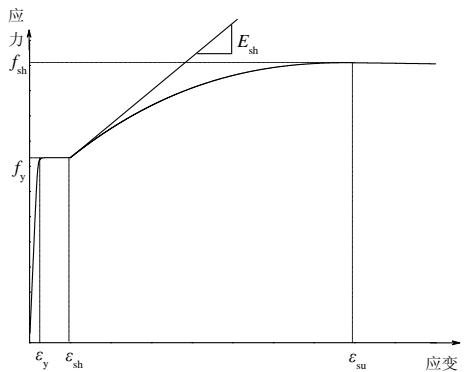
图 2 Rinforcingsteel 骨架曲线
Fig.2 Backbone curve of Reinforcingsteel
表 3 屈曲和损伤参数值
Table 3 Parameter values of buckling and damage
| 试件编号 | 屈曲参数 | 疲劳和强度退化参数 | |||||
|---|---|---|---|---|---|---|---|
| lsr | \beta | r | \gamma | Cf | \alpha | Cd | |
| TP010 | 6.0 | 1.0 | 0.5 | 0.5 | 1.0 | 0.506 | 0.85 |
| TP011 | 6.0 | 1.0 | 0.66 | 0.5 | 1.0 | 0.506 | 0.95 |
| TP012 | 6.0 | 1.0 | 0.75 | 0.5 | 1.0 | 0.506 | 1.0 |
| TP013 | 6.0 | 1.0 | 0.6 | 0.5 | 1.0 | 0.506 | 1.0 |
表 4 核心混凝土参数值
Table 4 Parameter values of core concrete
| 试件编号 | f_{\mathrm{cp}}/\mathrm{MPa} | \varepsilon_{\mathrm{c0}} | f_{\mathrm{pcu}}/\mathrm{MPa} | \varepsilon_{\mathrm{u}} |
|---|---|---|---|---|
| TP010 | -23.895 | -0.00227 | -4.779 | -0.0137 |
| TP011 | -23.495 | -0.00228 | -4.699 | -0.01368 |
| TP012 | -23.195 | -0.00228 | -4.639 | -0.0137 |
| TP013 | -23.852 | -0.00228 | -4.7704 | -0.01368 |
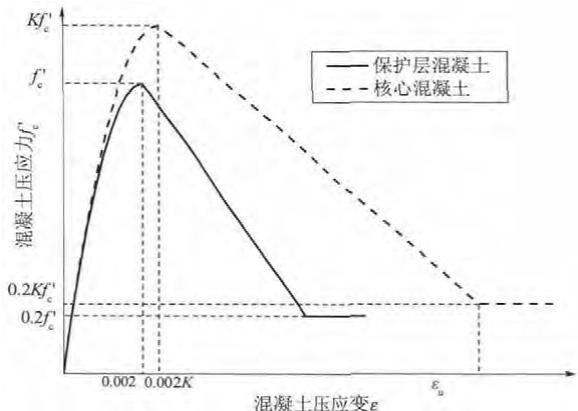
图 3 Concrete01 骨架曲线
Fig.3 Backbone curve of Concrete01
单元类型采用力法非线性梁柱单元 (nonlinearBeamColumn),单元划分分 3 种情况:单元长度为 l_{\mathrm{p}} 积分点个数为 2(该模型记为 M1I2)、单元长度为 3l_{\mathrm{p}} 积分点个数为 3(该模型记为 M3I3) 和单元长度为 6l_{\mathrm{p}} 积分点个数为 4(该模型记为 M6I4),有限元模型如图 4 所示。由于篇幅所限,对于有限元模型中使用的单元或材料模型的详细信息,此处不再赘述,可参见文献16。
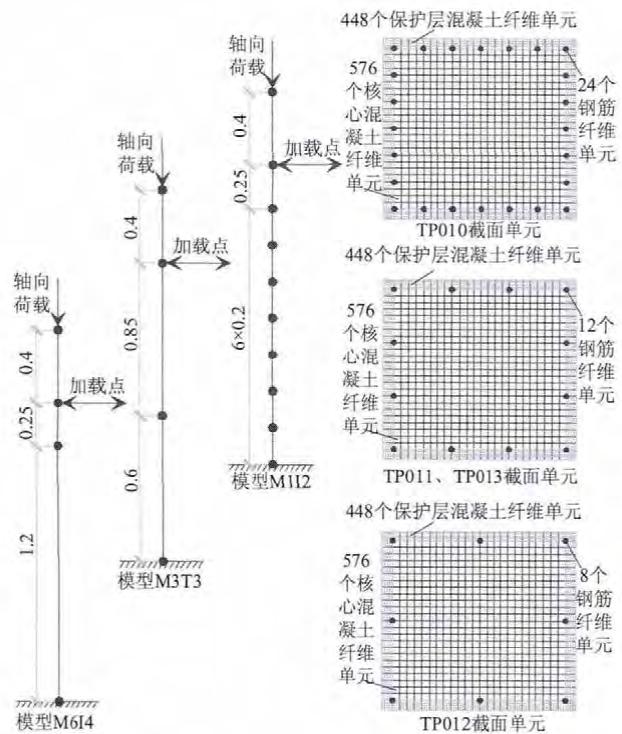
图 4 构件及截面有限元模型
Fig.4 FEM of members and sections
2.2 力-位移结果验证
由文献5可知,对于应变软化模型,积分点的个数会使数值模型的计算结果失真,因此,此处对各数值模型的力 - 位移计算结果以及试验实测力 - 位移滞回曲线进行分析,以验证根据理论分析结果所建立的数值模型的正确性和稳定性。
该试验按位移控制加载,正式加载之前以 -0.003 \mathrm{~m} 的目标位移进行预加载,正式加载时各级控制位移分别为: 0.005 \mathrm{~m}, 0.01 \mathrm{~m}, 0.016 \mathrm{~m}, 0.022 \mathrm{~m}, 0.027 \mathrm{~m}, 0.034 \mathrm{~m}, 0.04 \mathrm{~m}, 0.045 \mathrm{~m}, 0.051 \mathrm{~m}, 0.057 \mathrm{~m} 和 0.062 \mathrm{~m} ,每级控制位移循环 3 次,数值模拟分析时采用与试验相同的控制位移和加载方式。
图 5 列出了试验和数值模拟的力 - 位移关系曲线,从图中可看出,数值模拟结果与试验推倒曲线吻合较好,尤其是骨架曲线基本一致,在曲线与纵坐标的交点处偏差稍大,这主要是由于墩底主筋的粘结滑移效应所致。另外,材料参数的离散性以及塑性变形模拟的近似性等,都会导致数值模拟结果与试验推倒曲线的误差。
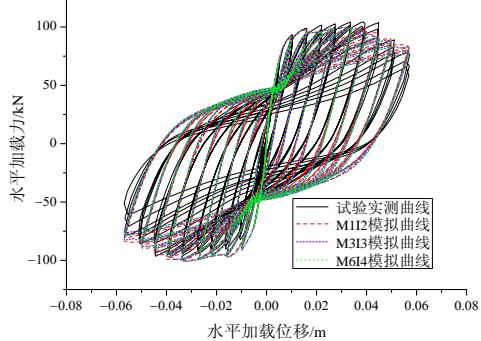
(a) TP010
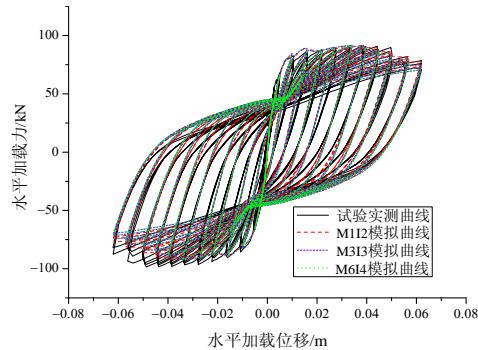
(b) TP011
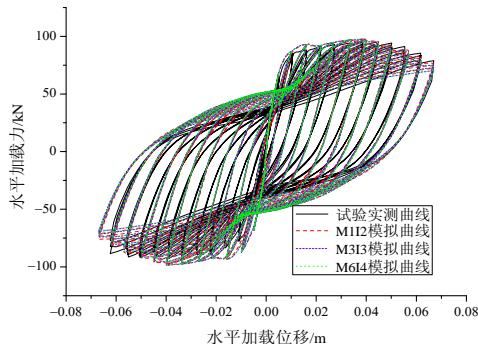
(c) TP012
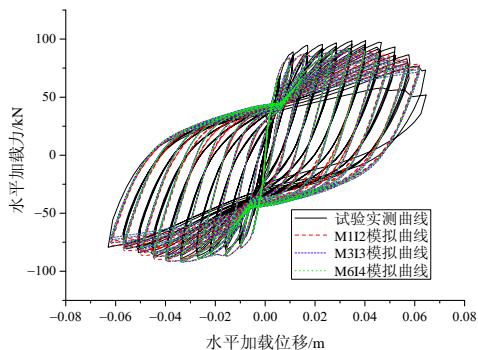
(d) TP013
图 5 试验实测力位移曲线与数值模拟曲线
Fig.5 Measured force-displacement curve and the numerical simulation curve
从图 5 还可看出,模型 M1I2、M3I3 和 M6I4 的分析结果完全一致,这就说明当积分点个数变化时,采用表 1 所示的单元长度划分可获得稳定的分析结果,不存在结构整体力 - 位移的数值计算结果失真问题。
为进一步证明这一点,将 M1I2 数值模型的积分点个数变为 3(该模型记为 M1I3),将 M3I3 的积分点个数分别变为 2(该模型记为 M3I2) 和 4(该模型记为 M3I4),将 M6I4 的积分点个数分别变为 3(该模型记为 M6I3) 和 5(该模型记为 M6I5),分别进行同样的分析。图 6 列出了 TP011 的 M1I3、M3I2 和 M3I4 分析结果,M6I3 分析结果与 M3I2 类似,M6I5 分析结果与 M3I4 类似,其他构件的分析结果与 TP011 类似,此处均不再列出。从图 6 可看出,在单元长度不变的情况下增加积分点个数导致计算收敛困难,结果发散;减小积分点个数则导致计算结果与试验数据偏差较大,且在弹性阶段偏差就已经较大。
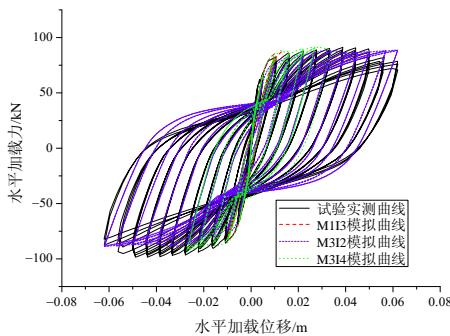
图 6 TP011 试验力位移实测曲线与数值模拟曲线 (变化积分点个数)
Fig.6 Measured force-displacement curve and the numerical simulation curve
2.3 曲率结果验证
由文献5可知,对于应变软化模型,积分点的个数不仅会使整体力 - 位移的数值计算结果失真,而且会使塑性铰处的局部截面变形计算结果失真,因此,此处也对其计算结果进行分析。
TP010~TP013 桥墩试件通过应变片对加载侧的墩底角隅主筋应变进行监测,应变片布置在墩底 25\mathrm{cm} 长度范围内,间距为 5\mathrm{cm} ,所得数据可从 http://seismic.csv.titech.ac.jp 网页上下载,由于应变片本身的局限性,所测得的钢筋屈服后应变数据并无实际意义。此处通过各数值模型计算得到的墩底截面曲率对比来评价模型单元划分和积分点个数选择的正确性。
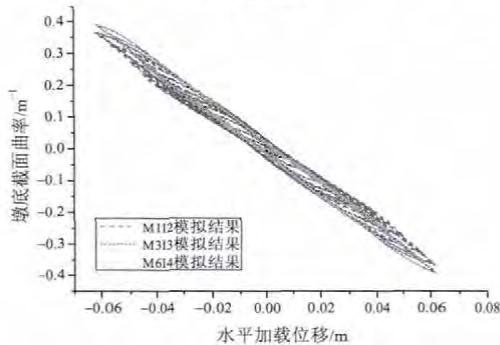
图 7 列出了各数值模型计算所得的墩底截面曲率滞回曲线。从图中可看出,对于构件 TP010 和 TP012,3 种数值模型的曲率计算结果吻合很好,对于构件 TP011 和 TP013,M1I2 的曲率计算结果略小于 M3I3 和 M6I4 的计算结果,M3I3 和 M6I4 的计算结果吻合很好,这说明在使用力法非线性梁柱单元时,积分点个数大于 2 时计算结果会更好,但是单元长度应与积分点个数对应,此时不存在塑性铰区域变形失真的问题。
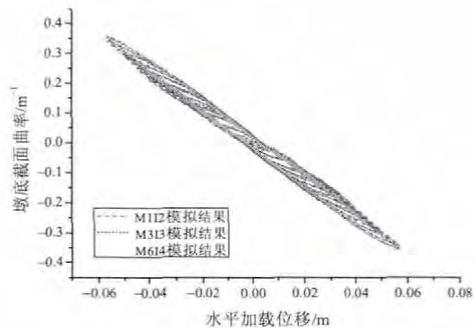
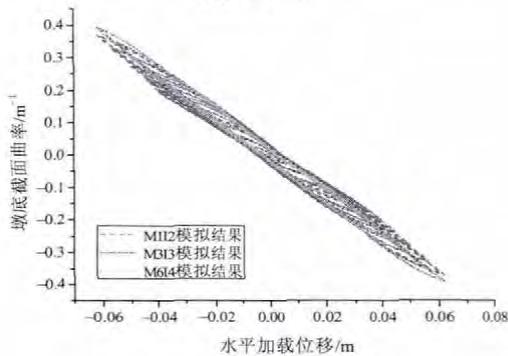
(a) TP010
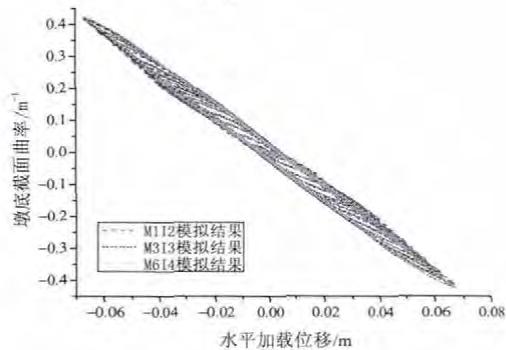
(b) TP011
(c) TP012
(d) TP013
图 7 墩底截面曲率数值模拟结果比较
Fig.7 Comparison between the section curvature curve at the pier bottom
3 结论
本文针对力法非线性梁柱单元模型,首先从理论上分析计算了不同积分点数对应的合理单元长度划分,然后基于 OpenSees 有限元程序,使用该理论分析结果建立了一组单墩循环推倒试验的数值分析模型,通过加载点力 - 位移滞回曲线的对比分析和墩底截面曲率滞回曲线的对比分析,得出以下结论:
(1) 使用力法非线性梁柱单元模型进行结构的非线性数值分析时,为消除其计算结果失真的问题,其单元长度划分应根据积分点数量确定,确定原则应该基于使单元屈服后变形增长的分布长度与塑性铰长度相等进行计算。
(2) 在实际使用中,可利用等效塑性铰长度代替塑性铰长度计算积分点数量与单元长度的关系,初步确定单元划分的合理长度。
(3) 由墩底截面曲率的对比分析可知,在使用力法非线性梁柱单元时,在保证单元长度与积分点数量的对应关系前提下,其积分点数量越多,计算结果越稳定。
参考文献:
Federal Emergency Management Agency (FEMA). NEHRP guidelines for the seismic rehabilitation of building [S]. Report No.FEMA-273, Washington, D.C. 1997. ↩
Zeris C A, Mahin S A. Analysis of reinforced concrete beam-columns under uniaxial excitation [J]. Journal of Structural Engineering, ASCE, 1988, 114(4): 804-820. ↩ ↩
Spacone E, Filippou F C, Taucer F F. Fibre beamcolumn model for nonlinear analysis of R/C frames I: Formulation [J]. Earthquake Engineering and Structure Dynamic, 1996, 25(7): 711-725. ↩
Neuenhofer A, Filippou F C. Evaluation of nonlinear frame finite-element models [J]. Journal of Structural Engineering, 1997, 123(7): 958-966. ↩ ↩
Coleman J, Spacone E. Localization issues in force-based frame elements [J]. Journal of Structural Engineering, 2001, 127(11): 1257-1265. ↩ ↩ ↩ ↩
Scott M H, Fenves G L. Plastic hinge integration methods for force-based beam-column elements [J]. Journal of Structural Engineering, 2006, 132(2): 244-252. ↩ ↩
Correial A A, Almeida J P, Pinho R. Force-based versus displacement-based formulations in the cyclic nonlinear analysis of rc frames [C]// Proceedings of the 14th World Conference on Earthquake Engineering. Beijing, China. 2008. ↩ ↩
Scott M, Fenves G, McKenna F, Filippou F. Software patterns for nonlinear beam-column models [J]. Journal of Structural Engineering, 2008, 134(4): 562-571. ↩ ↩
祷一,李忠献. 钢筋混凝土纤维梁柱单元实用模拟平台 [J]. 工程力学, 2011, 28(4): 102-108, 127. Zhuo Yi, Li Zhongxian. A practical simulation platform of reinforced concrete fiber beam-column element [J]. Engineering Mechanics, 2011, 28(4): 102-108, 127. (in Chinese) ↩
Park R, Paulay T. Reinforced concrete structures [M]. New York: John Wiley & Sons, 1975. ↩
Zhao X M, Wu Y F, Leung A Y, Lam H F. Plastic hinge length in reinforced concrete flexural members [J]. Procedia Engineering, 2011, 14: 1266-1274. ↩
Paulay T, Priestley M J N. Seismic design of reinforced concrete and masonry buildings [M]. New York: John Wiley & Sons, 1992. ↩
Gomes A, Appleton J. Nonlinear cyclic stress-strain relationship of reinforcing bars including buckling [J]. Engineering Structure, 1997, 19(10): 822-826. ↩
Brown J, Kunnath S K. Low cycle fatigue behavior of longitudinal reinforcement in reinforced concrete bridge columns [R]. MCEER Technical Report 00-0007, State University of New York, Buffalo, 2000. ↩
Scott B D, Park R, Priestley M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates [J]. ACI Journal, 1982, 79: 13-27. ↩ ↩
Mazzoni S, McKenna F, Scott M H, Fenves GL, et al. Open system for earthquake engineering simulation (OpenSees): user manual [EB]. http://opensees.berkeley.edu, 2006. ↩