基于拟可积Hamilton系统的铁路桥梁动力可靠度计算研究
期刊论文

基于拟可积Hamilton系统的铁路桥梁动力可靠度计算研究

赫中营^{1,3}, 王根会^{2}, 叶爱君^{3}, 夏修身^{2}

（1. 河南大学 土木建筑学院，河南 开封 475004；2. 兰州交通大学 土木工程学院，甘肃 兰州 730070；3. 同济大学 土木工程防灾国家重点实验室，上海 200092)

摘要

铁路运输提速增载，迫切需要对铁路桥梁动力可靠度进行研究。本文基于振型空间，首先推导出结构体系的广义动能和势能，继而基于拟 Hamilton 系统理论，推导出铁路混凝土桥梁的拟可积 Hamilton 系统方程。只考虑横向和扭转位移，得到铁路混凝土桥梁的条件可靠性函数所满足的 BK 方程及其定量边界、初值条件，可用中心差分法进行求解。以实际桥梁为算例，用上述方程求解其在列车荷载下的动力可靠度，得出或验证了与实际情况相符的若干重要结论，结果表明：动力可靠度和概率密度峰值，随桥梁初始能量的增大而减小，随桥梁边界能量的增大而增大；不同跨度桥梁分析结果与实际情况相符，说明基于拟可积 Hamilton 系统理论计算铁路桥梁的动力可靠度是可行的。

关键词：拟可积 Hamilton 系统；动力可靠度；铁路桥梁；有限差分法

中图分类号：U24 文献标志码：A doi:10.3969/j.issn.1001-8360.2016.05.017

Research on Calculation of Dynamic Reliability of Existing Railway Bridge Based on Quasi-Integrable-Hamiltonian Theory

HE Zhongying^{1,3}, WANG Genhui^{2}, YE Aijun^{3}, XIA Xiushen^{2}

(1. School of Civil Engineering and Architecture, Henan University, Kaifeng 475004, China;
2. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;
3. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract

Due to faster speed and heavier load of railway transportation, there is a pressing need to study dynamic reliability of railway bridges. In this paper, the generalized kinetic energy and potential energy expressions were first deduced in the mode shape space for structural system. Further, based on the Quasi-Hamiltonian system theory, the Quasi-Integrable-Hamiltonian system equation for railway concrete bridges was established in the mode space. With only the lateral and torsional displacements of railway bridges being considered, the backward Kolmogorov equation governing conditional reliability function has been obtained with its corresponding quantitative boundary and initial conditions, which can be solved by the central finite-difference method. In the case of actual bridges, the above equation was used to calculate dynamic reliability of exited railway PC bridges under dynamic train load. Some important conclusions that agreed with the actual situation were drawn and verified. The results showed that the dynamic reliability and peak value of probability density decreased with the increase of the primary energy of the bridge and increased with the increase of the boundary energy of the bridge. The results of the contrastive analysis of railway bridges with different spans were consistent with the actual situation, proving the feasibility to calculate the dynamic reliability for railway bridges using the Quasi-Integrable-Hamiltonian system theory.

Key words: Quasi-Integrable-Hamiltonian system; dynamic reliability; railway bridge; finite-difference method

PDF BibTeX

引言

铁路桥梁在服役期间，将不可避免地受到诸如地震、风和车辆等动力荷载的作用，动力破坏是其最主要的失效模式之一1。由于铁路桥梁在铁路运输网中具有特殊地位，其动力破坏将造成交通运输中断，甚至车毁人亡。自 1997 年以来，我国铁路运输大幅度提速增载，使一些既有铁路桥梁出现振幅和频率超限问题，桥梁的动力工作性能面临着巨大的挑战，迫切需要对铁路桥梁动力可靠性的分析计算2。因此，研究铁路桥梁结构的动力可靠性将具有十分重要的理论价值和经济、社会效益。

结构动力可靠性理论是用结构动力学和概率论相结合的方法研究结构在动力随机荷载作用下的可靠性及相应的设计方法。经过七十余年的发展，国内外结构动力可靠性理论取得了重要成果，并逐步得到完善，其分析方法主要分为以下三类3：(1) 基于随机振动理论解析解的动力可靠度计算方法；(2) 基于 Monte Carlo 法的动力可靠度计算方法；(3) 将动力可靠度问题转化为系统可靠度问题的计算方法。另外，近年来同济大学李杰和陈建兵4,5基于概率密度演化理论，建立了结构随机响应分析和动力可靠度分析的广义概率密度演化方程，可求解线性、非线性及随机结构的随机结构反应及动力可靠度，在结构的动力可靠度分析中也得到了一定应用。

由于动力可靠性分析计算的复杂性，对于第一类方法，即使对简单的首超失效问题，只有 Rice S. O. 6,7于 1945 年提出精确解，那也是针对一定前提下的简单情况。我国工程院院士朱位秋先生等8,9,10,11提出的随机动力学与控制的哈密顿理论体系（Hamiltonian system），为研究多自由度体系哈密顿系统的首超问题、估计首超概率及平均首超时间提供了新的思路和解决方法。本文基于哈密顿理论体系中的拟可积 Hamilton 系统12,13,14,15，推导出了铁路桥梁的等价拟可积 Hamilton 方程，确定了其在列车荷载作用下的条件可靠度函数及其初始条件和边界条件，并将理论推导公式应用于一座实际桥梁，对其动力可靠度进行分析，验证了该方法的合理性和适用性。

1 既有铁路桥梁的等价拟可积Hamilton系统

所谓等价拟可积 Hamilton 系统，是指状态参数（广义动量、广义速度等）与相应 Hamilton 函数（可积）之间满足一定关系的物理力学体系。铁路桥梁的广义动量、广义速度与其相应可积 Hamilton 函数之间满足的这种物理力学关系（方程）即可称为其等价拟可积 Hamilton 系统。

在外荷载激励下，铁路桥梁结构体系的振动方程可写为16

\mathbf{M}\ddot{\mathbf{s}} + \mathbf{C}\dot{\mathbf{s}} + \mathbf{K}\mathbf{s} = \mathbf{f}(t) \tag{1}

式中：\mathbf{M},\mathbf{C},\mathbf{K}分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；\mathbf{s}, \dot{\mathbf{s}}和\ddot{\mathbf{s}}分别为各自由度的位移、速度和加速度列向量，是关于时间t的函数；\mathbf{f}(t)为外部激励荷载。

为便于能量分析，将结构体系的动力学力向量分为保守的和非保守的分量，则式（1）可改写为

\mathbf{M}\ddot{\mathbf{s}} + \mathbf{K}\mathbf{s} = \mathbf{f}(t) - \mathbf{C}\dot{\mathbf{s}} \tag{2}

式（2）等式左边为结构惯性力和结构抗力组成的保守力向量，等式右端为外作用力和阻尼力组成的非保守力向量。

对于空间结构，基于有限元法的能量表达式中未知参数个数为结点个数的 6 倍，这给计算带来很大的困难17。因此，可考虑利用振型叠加方法表示铁路混凝土桥梁的振动位移，则其能量表达式将得到极大简化。

对于桥梁结构动力方程的解\mathbf{s}，可通过结构的振型表示为

\mathbf{s}=\phi_1 q_1 + \phi_2 q_2 + \cdots + \phi_n q_n = \sum_{i=1}^{n} \phi_i q_i \tag{3}

式中：\phi_i (i=1,\ldots,n)为结构振型，可通过特征方程求得；q_i (i=1,\ldots,n)为振型空间中的坐标值，称为广义坐标或结构的正则坐标，表示第i振型(\phi_i)的贡献。

如果假定阻尼矩阵也适用正交条件，将式（3）代入到式（2），并前乘第i个振型向量的转置\phi_i^\text{T}，可得

M_i \ddot{q}_i + K_i q_i = \phi_i^\text{T} \mathbf{f}(t) - C_i \dot{q}_i \tag{4}

式中：i=1,\ldots,n; M_i=\phi_i^\text{T} \mathbf{M}\phi_i, C_i=\phi_i^\text{T} \mathbf{C}\phi_i, K_i=\phi_i^\text{T} \mathbf{K}\phi_i分别为结构的广义质量、广义阻尼和广义刚度。

对于线性n自由度离散结构体系，\phi_i为n维列向量，其动能和势能可分别表示为

T=\frac{1}{2} m_{kl} \phi_{ik} \phi_{jl} \dot{q}_i \dot{q}_j = \frac{1}{2} \phi_i^\text{T} m \phi_j \dot{q}_i \dot{q}_j = \frac{1}{2} m_{ij} \dot{q}_i \dot{q}_j
V=\frac{1}{2} k_{kl} \phi_{ik} \phi_{jl} q_i q_j = \frac{1}{2} \phi_i^\text{T} k \phi_j q_i q_j = \frac{1}{2} k_{ij} q_i q_j
i=1,2,\ldots,n \tag{5}

如果体系的各振型对应的频率都不相等，则任意两个不同的振型，质量和刚度适用正交条件，式（5）简化为

T=\frac{1}{2} m_i \dot{q}_i^2
V=\frac{1}{2} k_i q_i^2
i=1,2,\ldots,n \tag{6}

对于连续结构体系，\phi_i可表示为结构轴向坐标的函数，质量和刚度也都是结构轴向坐标的函数，线性体系的动能和势能可表示为

T=\frac{1}{2} \int_0^L m \phi_i \phi_j dx \cdot \dot{q}_i \dot{q}_j = \frac{1}{2} m_{ij} \dot{q}_i \dot{q}_j
V=\frac{1}{2} \int_0^L k \phi_i \phi_j dx \cdot q_i q_j = \frac{1}{2} k_{ij} q_i q_j
i=1,2,\ldots,n \tag{7}

如果体系的各振型对应的频率都不相等，式（7）简化为

T=\frac{1}{2} \int_0^L m \phi_i^2 dx \cdot \dot{q}_i^2 = \frac{1}{2} m_i \dot{q}_i^2
V=\frac{1}{2} \int_0^L k \phi_i^2 dx \cdot q_i^2 = \frac{1}{2} k_i q_i^2
i=1,2,\ldots,n \tag{8}

该桥梁结构体系对应的 Lagrange 函数为

L=L(q, \dot{q},t) = \frac{1}{2} m_{ij} \dot{q}_i \dot{q}_j - \frac{1}{2} k_{ij} q_i q_j - U
i=1,2,\ldots,n \tag{9}

式中：U=\phi_i^\text{T} \mathbf{f}(t)q_j - c_{ij} \dot{q}_i q_j为非保守力所做的功；c_{ij}为阻尼系数。 q_i与\dot{q}_i分别为广义位移（坐标）与广义速度，广义动量可定义为18

p_i = \frac{\partial L}{\partial \dot{q}_i} = m_{ij} \dot{q}_j
i=1,2,\ldots,n \tag{10}

式 (10) 称为由 Lagrange 函数L生成的 Legendre 变换，式 (10) 为非奇异变换、可逆，则其逆变换也是 Legendre 变换。据 Legendre 变换的逆变换定理，式 (10) 之逆变换的生成函数为

(p_i \dot{q}_i - L)_{\dot{q}_i \to p_i} = H(q,p,t) \tag{11}

H(q,p,t)即为 Hamilton 函数，其表达式为

H=\frac{1}{2} m_{ij}^{-1} p_i p_j + \frac{1}{2} k_{ij} q_i q_j + U^{-1}
i=1,2,\ldots,n \tag{12}

则结构以q_i,p_i为基本变量的 Hamilton 方程为

\dot{q}_i = \frac{\partial H}{\partial p_i}
\dot{p}_i = - \frac{\partial H}{\partial q_j}
i=1,2,\ldots,n \tag{13}

以F_i^\text{d}=-c_{ij}(q,p)\partial\bar{H}/\partial p_i记随机激励的耗散的 Hamilton 系统的耗散力。以F_i^\text{e}=f_{ik}(q,p)\zeta_k(t)记耗散的 Hamilton 系统的激励力，可根据 Hamilton 原理和 Legendre 变换导出 Gauss 白噪声激励下n自由度耗散 Hamilton 系统的运动微分方程形为

\dot{q}_i = \frac{\partial \bar{H}}{\partial p_i}
\dot{p}_i = - \frac{\partial \bar{H}}{\partial q_i} - c_{ij}(q,p) \frac{\partial \bar{H}}{\partial p_i} + f_{ik}(q,p)\zeta_k(t)
i,j=1,2,\ldots,n; k=1,2,\ldots,m \tag{14}

式中：\bar{H}=\bar{H}(q,p)为未扰 Hamilton 系统的 Hamilton 函数；\zeta_k(t)为激励荷载强度的 Gauss 白噪声。

显然，对于桥梁结构等耗散的 Hamilton 系统，f_{ik}不依赖于p，Wong-Zakai 修正项为 0，从而\bar{H}=H，则式 (14) 等价的 Ito 随机微分方程为

dq_i = \frac{\partial H}{\partial p_i} dt
dp_i = - \left( \frac{\partial H}{\partial q_i} + c_{ij}(q,p) \frac{\partial H}{\partial p_i} \right) dt + \sigma_{ik}(q,p) dB_k(t)
i=1,2,\ldots,n \tag{15}

式中：B_k(t)为第k维标准 Wiener 过程。

设阻尼力与随机激励强度同为\varepsilon阶小量，即

c_{ij}=\varepsilon c'_{ij}
\sigma_{ik}=\varepsilon^{1/2} \sigma'_{ik} \tag{16}

式中：\varepsilon为一正小参数；c'_{ij}、\sigma'_{ik}为有限量。

式（15）可改写成

dq_i = \frac{\partial H}{\partial p_i} dt
dp_i = - \left[ \frac{\partial H}{\partial q_i} + \varepsilon c'_{ij}(q,p) \frac{\partial H}{\partial p_j} \right] dt + \varepsilon^{1/2} \sigma'_{ik}(q,p) dB_k(t)
i,j=1,2,\ldots,n; k=1,2,\ldots,m \tag{17}

式 (17) 称为拟 Hamilton 系统，对应于H(q,p)为可积函数的系统称为拟可积 Hamilton 系统。

在物理上，只要振动一周，随机激励输入系统的能量与阻尼消耗的能量之差同系统本身能量相比为小，即可视为拟 Hamilton 系统。

根据以上的等价拟可积 Hamilton 系统理论，铁路混凝土桥梁系统的广义动量、广义速度、Hamilton 函数及拟 Hamilton 方程为

p_i = m_{ij} \dot{q}_j \tag{18}
\dot{q}_i = m_{ij}^{-1} p_j \tag{19}
H=\frac{1}{2} m_{ij}^{-1} p_i p_j + \frac{1}{2} k_{ij} q_i q_j + U^{-1} \tag{20}
\begin{cases} \dot{q}_i = \frac{\partial H}{\partial p_i} = m_{ij}^{-1} p_j \\ \dot{p}_i = - \frac{\partial \bar{H}}{\partial q_i} - c_{ij}(q,p) \frac{\partial \bar{H}}{\partial p_i} + f_{ik}(q,p)\zeta_k(t) = -k_{ij} q_j - c_{ij} p_i + f_{ik}(q,p)\zeta_k(t) \end{cases} \tag{21}

式 (18)～式(21) 的位移、质量、刚度和阻尼分别为广义振型坐标、广义质量、广义刚度和广义阻尼。

进一步，将式（4）两边同除以第i振型广义质量M_i，则可得

\ddot{q}_i + \omega_i^2 q_i = f_i(t)/M_i - 2\xi_i \omega_i \dot{q}_i
i=1,2,\ldots,n \tag{22}

式中：f_i(t)=\phi_i^\text{T} \mathbf{f}(t); \xi_i为第i振型阻尼比；\omega_i为第i振型相应的频率。

式（22）所示的振动结构体系，宏观上可视为各自由度互不耦合的n维单位质量振动体系，该体系对应的广义质量、广义阻尼和广义刚度可分别视为

m_{ij}=\begin{cases} 1 & i=j \\ 0 & i \neq j \end{cases}
c_{ij}=\begin{cases} 2\xi_{i(j)} \omega_{i(j)} & i=j \\ 0 & i \neq j \end{cases}
k_{ij}=\begin{cases} \omega_{i(j)}^2 & i=j \\ 0 & i \neq j \end{cases} \tag{23}

则其对应的广义动量、广义速度、Hamilton 函数及拟 Hamilton 方程为

p_i = \dot{q}_j \tag{24}
\dot{q}_i = p_j \tag{25}
H=\frac{1}{2} p_i p_j + \frac{1}{2} \omega_{i(j)}^2 q_i q_j + U^{-1} \tag{26}
\begin{cases} \dot{q}_i = p_i \\ \dot{p}_i = -\omega_i^2 q_i - 2\xi_i \omega_i p_i + \kappa_k \zeta_k(t) \end{cases} \tag{27}

式中：i=j=1,2,\ldots,n; k=1,2,\ldots,m; \kappa_i=f_{ik}(q,p)/m_i (i=1,2,\ldots,m)定义为激励荷载的第i维广义质量。

由式（26）可看出，该系统相应的 Hamilton 函数为可积函数，则该系统为拟可积 Hamilton 系统。

2 既有铁路混凝土桥梁动力可靠性分析

一般的桥梁结构体系均为连续结构体系，其各阶振型可用连续函数表示，取少数几个起控制作用的振型能准确地反应其振动特性，这就极大地减少了计算 Hamilton 系统时的位移和动量参数。

此处仅考虑铁路混凝土桥梁的横向位移和扭转位移，并以随机量(Q,P)代替(q,p)，则根据式（27），其运动微分方程为

\begin{cases} \dot{Q}_1 = P_1 \\ \dot{P}_1 = -2\xi_1 \omega_1 P_1 - \omega_1^2 Q_1 + \kappa_1 \zeta_1 \\ \dot{Q}_2 = P_2 \\ \dot{P}_2 = -2\xi_2 \omega_2 P_2 - \omega_2^2 Q_2 + \kappa_2 \zeta_2 \end{cases} \tag{28}

式中：下标 1 表示横向位移各参数；下标 2 表示扭转位移各参数；\zeta_1,\zeta_2分别表示横向和扭转激励源，是强度为2D_i的独立高斯白噪声；\kappa_i = \int_0^L m_{\zeta i} \phi_i dx / \int_0^L m_i \phi_i^2 dx。相应的 Hamilton 函数为H=H_1+H_2，其中H_i = (p_i^2 + \omega_i^2 q_i^2)/2。设\omega_i不满足共振关系，按文献19中的随机平均法，可得式 (28) 的平均 Ito 方程为12

dH_r = \bar{m}_r(H_1,H_2)dt + \bar{\sigma}_{rk} \bar{\sigma}_{sk}(H_1,H_2)dB_k
r=1,2; k=1,2 \tag{29}

式中：\bar{m}_r(H_1,H_2)=-2\xi_r \omega_r H_r + \kappa_r D_r；当r=s时，\bar{\sigma}_{rk} \bar{\sigma}_{sk}(H_1,H_2)=2\kappa_r D_r H_r，当r \neq s时，\bar{\sigma}_{rk} \bar{\sigma}_{sk}(H_1,H_2)=0。根据 Ito 微分法则，其条件可靠性函数R(t|H_{10},H_{20})满足下列后向 Kolmogorov 方程12

\frac{\partial R}{\partial t} = \bar{m}_1 \frac{\partial R}{\partial H_{10}} + \frac{1}{2} \bar{\sigma}_{1k} \bar{\sigma}_{1k}(H_0) \frac{\partial^2 R}{\partial H_{10}^2} + \bar{m}_2 \frac{\partial R}{\partial H_{20}} + \frac{1}{2} \bar{\sigma}_{2k} \bar{\sigma}_{2k}(H_0) \frac{\partial^2 R}{\partial H_{20}^2} \tag{30}

初始条件为

R(0|H_0)=1
H_0 \in \Omega \tag{31}

设安全域边界由\Gamma_c和\Gamma_0组成，见图 1，即

\begin{cases} \Gamma_c : H_1 + H_2 = H_c, H_1,H_2 \geqslant 0 \\ \Gamma_0 = \Gamma_{01} + \Gamma_{02} + \Gamma_{03} \\ \Gamma_{01} : H_1 = 0, 0 < H_2 < H_c \\ \Gamma_{02} : H_2 = 0, 0 < H_1 < H_c \\ \Gamma_{03} : H_1 = H_2 = 0 \end{cases} \tag{32}

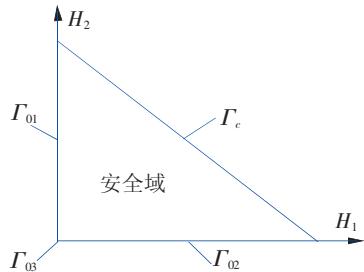
1-XVbQ.jpg

图 1 安全域及其边界

相应定量边界条件为

\Gamma_c : R(t|H_{10},H_{20})=0
\Gamma_{01} : \frac{\partial R}{\partial t} = \kappa_1 D_1 \frac{\partial R}{\partial H_{10}} + \kappa_2 D_2 H_{20} \frac{\partial^2 R}{\partial H_{20}^2} + (-2\xi_2 \omega_2 H_{20} + \kappa_2 D_2) \frac{\partial R}{\partial H_{20}}
\Gamma_{02} : \frac{\partial R}{\partial t} = \kappa_2 D_2 \frac{\partial R}{\partial H_{20}} + \kappa_1 D_1 H_{10} \frac{\partial^2 R}{\partial H_{10}^2} + (-2\xi_1 \omega_1 H_{10} + \kappa_1 D_1) \frac{\partial R}{\partial H_{10}}
\Gamma_{03} : \frac{\partial R}{\partial t} = \kappa_1 D_1 \frac{\partial R}{\partial H_{10}} + \kappa_2 D_2 \frac{\partial R}{\partial H_{20}} \tag{33}

对于上述偏微分方程，可用有限差分法进行数值求解20。只考虑在离散能量点H_{1i}=i\Delta H_1 (i=0,1,\ldots,N_1)、H_{2j}=j\Delta H_2 (j=0,1,\ldots,N_2)和离散事件点t_n=n\Delta t(n=0,1,\ldots)的R(t|H_1,H_2)的值，H_{1i}/H_{2j}和t_n将空间(H_1,H_2,t)化分成矩形网格，将R的一阶和二阶导数用相邻点的R值表示，代入后向 Kolmogorov 方程和边界条件，就能由已知的初值求出任意点在任意时刻的R值。

3 工程算例

西安铁路局管内阳（平关）—安（康）线于 60 年代末“三线”建设时期修建，为单线 I 级干线，电力牵引区段，全长351.566\text{km}，牵引定数4000\text{t}，通行能力为37.5对 / 天。线路允许速度100\text{km/h}，全线共有桥梁351座 /27221延米；其中圬工桥347座 /1016孔（23.8\text{m}跨度预应力圬工梁369孔，31.7\text{m}跨度预应力圬工梁255孔），这两种跨度的预应力钢筋混凝土梁图号分别为“大 (65)138”、“叁标外桥 006A”、“丰 70−1”、“丰 70−2”、“叁标桥 2019" 等。跨度23.8\text{m}的预应力梁 ANSYS 模型及单片 T 梁的截面特性分别如图 2(a) 和图 2(b) 所示（31.7\text{m}的预应力梁模型及截面特性与23.8\text{m}梁相似）。

3.1 计算参数的取值

从第 2 节的分析可看出，在计算桥梁的条件可靠性函数时，需要知道桥梁结构的自振频率、阻尼比、激励强度等。对于阳安线混凝土桥梁，阻尼比取最大阻尼比\xi=0.051；激振源取文献1中随机模拟的82\text{km/h}的货车构架加速度蛇形波，强度为D=\sigma_p=100\text{cm/s}^2，文献19中已证明该随机蛇行波为平稳 Gauss 过程，此处进一步假设其为 Gauss 白噪声过程；一节货车质量取为80000\text{kg}，每个构架对应的质量取为m_{\text{ 车}}=40000\text{kg}21；参考文献1的研究成果，桥梁横向和扭转的一阶振型函数取为\phi_i(x)=\sin\pi x/L, m_1=\rho Ax, m_2=h^3 m_1/3, \rho=2.6\times 10^3\text{kg/m}^3为混凝土密度，A=1.618\text{m}^2为 T 梁截面，h=2.46\text{m}为 T 梁高度。用有限元计算软件 ANSYS 计算出23.8\text{m}梁的一阶横向和扭转频率分别为4.543\text{Hz}和12.277\text{Hz}，31.7\text{m}梁的一阶横向和扭转频率分别为3.036\text{Hz}和8.905\text{Hz}17。用中心有限差分法（边界处用向前差分法）计算可靠性函数和可靠性概论密度函数时，参照文献20中的精度要求并经必要试算，取N_1=N_2=N=51（即将H_1,H_2等分为51份），dt=0.004\text{s}（即计算时间间隔为0.004\text{s}）。对于桥梁的临界破坏能量H_c，可根据规范规定的振幅界限、列车脱轨能量界限或桥梁结构破坏能量等不同的依据和计算需要确定。因目前对铁路桥梁的各种临界能量并无明确的取值和计算规定，此处所取的临界能量仅为分析比较之用。

2-ADis.jpg

3-lcOS.jpg

(a) 有限元模型; (b) T 梁截面特性 (单位：m)

图 2 23.8m 梁有限元模型及界面特性

3.2 计算结果分析

用 MATLAB 编写程序计算 M 文件JS1.m按式（30）求解条件可靠性函数R(t)和转移概率密度函数p(t)22。23.8\text{m}梁的计算结果如图 3(a)～3(h) 所示。31.7\text{m}梁可靠性函数R(t)、概率密度p(t)与23.8\text{m}梁相似，部分图形如图 4(a)、4(b) 所示。

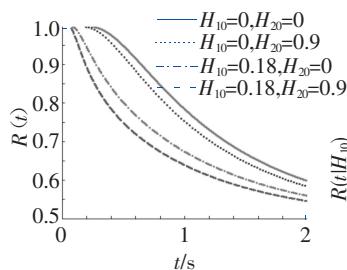
4-dMou.jpg

(a) R(t|H_{c1}=1,H_{c2}=5);

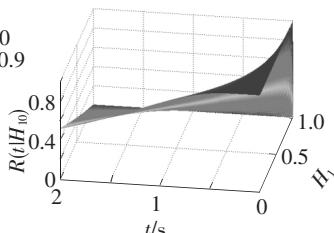
5-eBBn.jpg

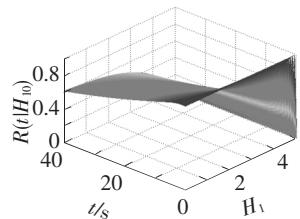
(b) R(t,H_{10}|H_{c1}=1,H_{c2}=5)(H_{20}=0);

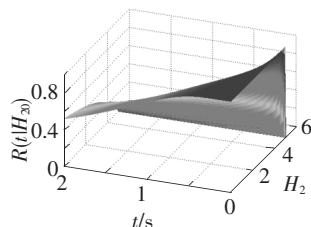
6-yZlD.jpg

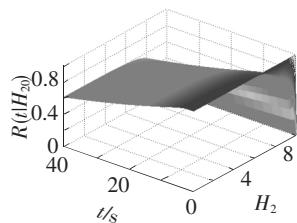
(c) R(t,H_{20}|H_{c1}=1,H_{c2}=5)(H_{10}=0);

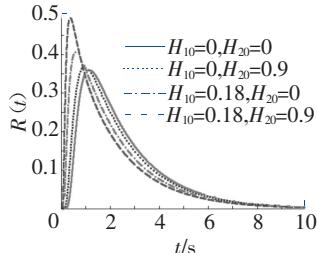
7-Qhyu.jpg

(d) p(t|H_{c1}=1,H_{c2}=5);

8-oAmH.jpg

(e) R(t|H_{c1}=5,H_{c2}=10);

9-ZLVo.jpg

(f) R(t,H_{10}|H_{c1}=5,H_{c2}=10)(H_{20}=0);

10-ytTY.jpg

(g) R(t,H_{20}|H_{c1}=5,H_{c2}=10)(H_{10}=0);

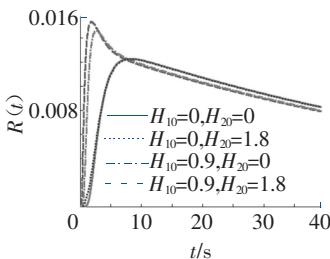
11-GwFc.jpg

(h) p(t|H_{c1}=5,H_{c2}=10)
图 3 23.8m 梁 R(t) 和 p(t) 计算图

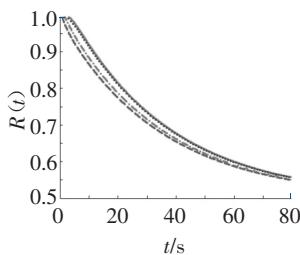
12-nWwl.jpg

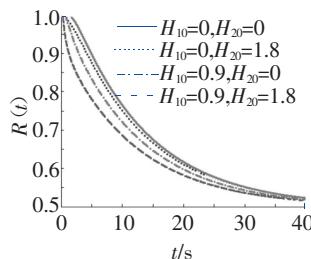
(a) R(t|H_{c1}=5,H_{c2}=10) (H_{10}=0,H_{20}=0; H_{10}=0.9,H_{20}=0; H_{10}=0,H_{20}=1.8; H_{10}=0.9,H_{20}=1.8);

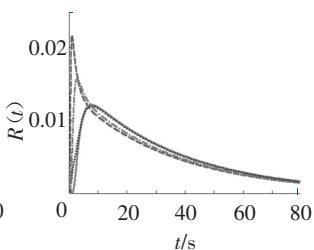
13-NHbE.jpg

(b) p(t|H_{c1}=5,H_{c2}=10) (H_{10}=0,H_{20}=0; H_{10}=0.9,H_{20}=0; H_{10}=0,H_{20}=1.8; H_{10}=0.9,H_{20}=1.8)
图 4 31.7m 梁 R(t) 和 p(t) 计算图
从图 3、图 4 中可以看出：

（1）桥梁初始能量越大，则桥梁的可靠性越低；
（2）桥梁的临界能量H_{c1},H_{c2}越大，则桥梁的可靠性越高，可靠性由H_{c1},H_{c2}共同控制；
（3）桥梁的初始能量越大，则其概率密度的峰值越大，概率密度函数的分布越集中；
（4）桥梁的临界能量H_{c1},H_{c2}越大，则其概率密度函数的峰值越小，概率密度函数的分布越均匀。

实际情况中，在其他参数（刚度等）相同的情况下，桥梁的初始能量较大，则意味着列车过桥前，桥梁的变形或振动较大，则列车过桥时，桥梁的破坏概率就较大，桥梁的可靠性较低；同样，桥梁的临界能量越大，意味着桥梁变形能力越强，桥梁的可靠性越高。

在相同条件下，H_{10}=H_{20}=0时23.8\text{m}梁和31.7\text{m}梁的可靠性对比见图 5，两者的可靠性差值见图 6。从图 5 和图 6 中可看出，在初始能量为零，临界能量相等的情况下，31.7\text{m}梁比23.8\text{m}梁的可靠性大，这说明，在其他参数相同的条件下，31.7\text{m}梁比23.8\text{m}梁的变形能力强，这与结构越柔变形能力越大的力学理论相符。

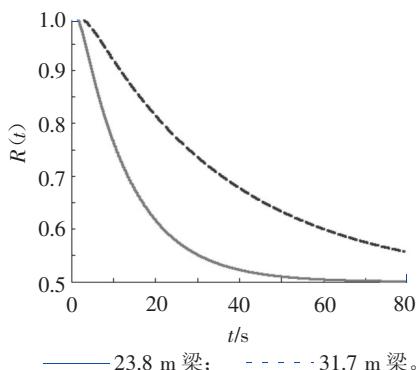
14-fypA.jpg

图 5 相同条件下 23.8m 和 31.7m 梁 R(t|H_c1=5,H_c2=10) 对比图 (H_{10}=0,H_{20}=0)

从以上分析可知，基于拟可积 Hamilton 系统的阳安线混凝土桥梁的动力可靠性函数符合实际情况，说明这种计算方法是合理的。

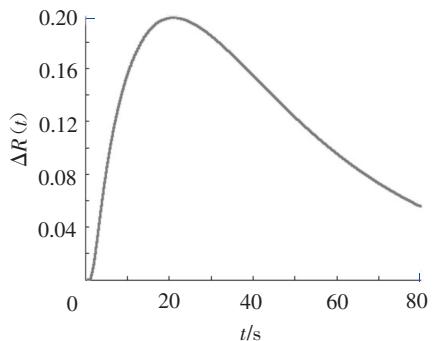
15-lCEB.jpg

图 6 相同条件下， 23.8m 和 31.7m 梁 R(t|H_c1=5,H_c2=10) 差值图 (H_{10}=0,H_{20}=0)

4 结论

本文通过对拟 Hamilton 系统理论的研究，基于振型叠加法建立了既有铁路混凝土桥梁的等价拟可积 Hamilton 系统方程。通过对此系统方程的分析，得出了铁路混凝土桥梁在 Gauss 白噪声激励下的条件概论可靠性函数和其定量边界条件、初值条件，借助 MATLAB 软件使得方程求解非常容易。工程算例分析结果表明，该方法对铁路桥梁的动力可靠性分析是合理的，分析结果和实际情况相符。

参考文献

  1. 曾庆元, 郭向荣. 列车桥梁时变系统振动分析理论与应用 [M]. 北京: 中国铁道出版社, 1999. ↩ ↩ ↩ ↩

  2. 郭文华, 曾庆元. 高速铁路多跨简支梁桥横向振动随机分析 [J]. 长沙铁道学院学报, 1997, 15(1): 1-9.
    GUO Wenhua, ZENG Qingyuan. Transverse Random Vibration Analysis for the High-speed Railway Multi-span Simply-supported Bridge [J]. Journal of Changsha Railway University, 1997, 15(1): 1-9. ↩

  3. 刘佩. 随机地震作用下结构动力可靠度计算方法研究 [D]. 北京：北京交通大学，2010. ↩

  4. LI J, CHEN J B. Stochastic Dynamics of Structures[M]. New York: John Wiley and Sons, 2009. ↩

  5. CHEN J B, LI J. A Note on the Principle of Preservation of Probability and Probability Density Evolution Equation[J]. Probabilistic Engineering Mechanics, 2009, 24(1): 51-59. ↩

  6. RICE S O. Mathematical Analysis of Random Noise[J]. Bell System Technical Journal, 1944, 23(3):282-332. ↩

  7. RICE S O. Mathematical Analysis of Random Noise-conclusion[J]. Bell System Technical Journal, 1945, 24(1): 146-156. ↩

  8. 朱位秋. 非线性随机动力学与控制 -Hamilton 理论体系框架 [M]. 北京：科学出版社，2004. ↩

  9. ZHU W Q, CAIG Q. Random Vibration of Viscoelastic System under Broad-band Excitations [J]. International Journal of Non-linear Mechanics, 2011, 46(5):720-726. ↩

  10. ZHU W Q, CAI G Q. Generation of Non-gaussian Stochastic Processes Using Nonlinear Filters[J]. Probabilistic Engineering Mechanics, 2014,36:56-62. ↩

  11. HU R C, YING Z G, ZHU W Q. Stochastic Minimax Optimal Control Strategy for Uncertain Quasi-hamiltonian Systems Using Stochastic Maximum Principle [J]. Structural and Multidisciplinary Optimization, 2014, 49(1):69-80. ↩

  12. ZHU W Q, DENG M L, HUANG Z L. First-passage Failure of Quasi-integrable-hamiltonian Systems [J]. ASME Journal of Applied Mechanics, 2002, 69(3): 274-282. ↩ ↩ ↩

  13. CHEN L C, DENG M L, ZHU W Q. First Passage Failure of Quasi Integrable Hamiltonian Systems under Combined Harmonic and White Noise Excitations[J]. Acta Mechanica, 2009, 206(3-4): 133-148. ↩

  14. CHEN L C, ZHU W Q. Reliability of Quasi Integrable Generalized Hamiltonian Systems[J]. Probabilistic Engineering Mechanics, 2010, 25(1):61-66. ↩

  15. LIU W Y, ZHU W Q, JIA W T. Stochastic Stability of Quasi-integrable and Non-resonant Hamiltonian Systems under Parametric Excitations of Combined Gaussian and Poisson White Noises[J]. International Journal of Nonlinear Mechanics, 2014, 58:191-198. ↩

  16. CLOUGH R W, PENZIEN J. Dynamics of Structures [M]. 3rd ed. Berkeley, California: Computers & Structures, Inc., 2003. ↩

  17. 赫中营. 基于拟 Hamilton 理论的既有铁路桥梁动力可靠性研究 [D]. 兰州：兰州交通大学，2008. ↩ ↩

  18. 陈滨. 分析动力学 [M]. 北京：北京大学出版社，1987. ↩

  19. 星谷胜. 随机振动分析 [M]. 常宝琦, 译. 北京: 地震出版社, 1977. ↩ ↩

  20. 陆金甫. 偏微分方程差分方法 [M]. 北京：高等教育出版社，1988. ↩ ↩

  21. 严隽奎. 车辆工程 [M]. 北京：中国铁道出版社，2003. ↩

  22. 刘卫国. MATLAB 程序设计教程 [M]. 北京：中国水利水电出版社，2005. ↩

评论
Copyright © 2025 桥梁抗震小站 All Rights Reserved. Powered by Halo.