罗富元 * 赫中营 叶爱君
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要
通过简化的力学模型,进行理论分析,得出在横向地震作用下,桥梁下部结构扭转效应的影响因素。结合一个实际桥梁工程,采用有限元分析方法,针对理论分析所得到的影响因素进行参数分析,得出各影响因素和扭矩的关系。通过两种方法所得结论的相互印证,最终确定扭转效应的影响因素。最后,通过对比计入扭转效应和忽略扭转效应时最不利单桩的受力情况,分析桥梁下部结构的扭转效应对最不利单桩受力的影响。
关键词
横向地震作用,桥梁下部结构,扭转效应,最不利单桩
\text{DOI}: 10.15935/j.cnki.jggcs.2015.03.020
Torsional Responses of Bridge Substructure under Lateral Seismic Loads
LUO Fuyuan* HE Zhongying YE Aijun
(State Key Laboratory for Disaster Reduction of Civil Engineering, Shanghai 200092, China)
Abstract
To explore the factors of the torsional response of bridge substructure under lateral seismic loading, two simplified mechanical models were constructed. The factors were obtained by mechanical analyses first. Based on a bridge project, a simulation of torsional response of bridge substructure with lateral seismic load was carried out. Simulation results were consistent with mechanical analyses. Finally, by comparing the internal force of the most dangerous piles in two cases, in which one were including the torsional effect and the other were neglecting the torsional effect, the impact of the torsional response of bridge substructure on the most dangerous pile was investigated.
Keywords
lateral seismic load, bridge substructure, torsional response, most dangerous pile
1 引言
由于在桥梁震害调查中,因桥梁下部结构的扭转效应而导致结构破坏的情况很少见,因此,目前针对地震作用下桥梁结构扭转效应的研究很少,而现有的研究对横向地震作用下桥梁下部结构的扭转效应的产生及影响更是没有涉及1,此外,现行的《公路桥梁抗震设计细则》(JTG/TB02—01—2008)2和《城市桥梁抗震设计规范》(CJJ166—2011)3对于桥梁结构构件抗震验算的规定,也并没有考虑地震作用下产生的扭矩对桥梁结构构件的影响。
对于建筑结构,由于历次震害调查结果表明,建筑结构在地震作用下的扭转效应是造成结构抗震性能退化,导致结构破坏甚至倒塌的重要原因4。所以在《建筑抗震设计规范》(GB50011—2010)5和《高层建筑混凝土结构技术规程》(JGJ3—2010)6中均有关于地震作用下考虑扭转效应的相关规定。而其中主要考虑的受力构件为刚性楼板下的边缘柱、墙等抗侧力构件。对于桥梁结构,由于在结构形式上,桥梁的承台和群桩基础的外围单桩与房屋结构的刚性楼板和边缘柱、墙等抗侧力构件有相似性,且群桩基础的外围单桩通常也是桥梁结构在地震作用下的最不利受力单桩,那么,如果在地震作用下桥梁下部结构产生很大的扭转效应,则按照规范而进行的抗震验算,显然会由于忽略扭转效应而存在导致计算结果偏不安全的可能。同时,由于桩基的隐蔽性,导致对桩基震害调查的困难,所以不能根据以往的桥梁震害调查结果而忽视桥梁下部结构的扭转效应7。因此,针对地震作用下桥梁下部结构产生扭转效应进行研究是十分必要的。
针对扭转效应而言,桥梁结构和房屋结构的区别主要体现在两个方面:① 房屋结构的楼板在自身平面内是无限刚性的,而桥梁结构的上部结构则一般是柔性的;② 房屋结构的楼板和柱、墙等抗侧力构件是固结的,所以楼板的扭转效应一定会有效地传递到这些抗侧力构件,而桥梁结构,除刚构桥及拱脚固结的拱桥外,其上部结构和下部结构之间的内力传递是通过支座实现的,所以支座可能对下部结构的扭转效应有一定的影响。
由于桥梁结构的质量在纵桥向和横桥向的分布一般是对称的,而在纵桥向,梁墩交接处的纵向约束布置通常也是对称的,且纵桥向的纵向抗弯刚度可视为无限大,所以在纵向水平地震作用下,其上部结构的运动可视为刚体运动,即纵向摆动,不会使下部结构产生扭转效应。
基于以上几点,本文只对横向水平地震作用下桥梁下部结构的扭转效应进行以下两部分研究:① 横向地震作用下桥梁下部结构扭转效应的影响因素;② 桥梁下部结构扭转效应对最不利单桩的受力影响。本文首先通过简化的力学模型,运用力学方法8,求解出在横向地震作用下,桥梁下部结构扭矩的计算公式,通过公式得出横向地震作用下桥梁下部结构扭转效应的影响因素,然后结合一个实际桥梁工程,通过建立有限元模型分析其横向地震作用下桥梁下部结构扭转效应的影响因素。通过简化力学模型和有限元模型分析结果的相互印证,最终确定横向地震作用下桥梁下部结构的扭转效应的影响因素。最后以同一个实际桥梁工程为背景,分析桥梁下部结构扭转效应对最不利单桩的受力影响。
2 基于简化力学模型的扭转效应分析
桥梁的墩梁可以通过固结和设置支座两种方式实现力的传递,为了研究支座对桥梁下部结构扭转效应的影响,需要建立两个简化力学模型:墩梁固结力学模型和实际桥梁工程常用支座布置形式下的一个简化力学模型。这两个模型除了墩梁连接方式不同外,其他参数均相同,而扭转效应的其他影响因素将主要在设置支座的力学模型中进行探讨。
2.1 模型一:墩梁固结力学模型
不考虑支座的影响,并为了简化分析,选取门式刚架作为墩梁固结力学模型进行理论分析。如图 1 所示,以主梁模拟桥梁的上部结构,墩柱模拟桥梁的下部结构,以 X 轴方向为纵向,Y 轴方向为横向,Z 轴为竖向,其中,E I_{1Z}, E I_{1Y}, G I_{1P} 分别为主梁截面的横向抗弯刚度、竖向抗弯刚度以及抗扭刚度;E I_{2X}, E I_{2Y}, G I_{2P} 分别为墩柱截面的横向抗弯刚度、纵向抗弯刚度、抗扭刚度。 P 为作用于主梁上的均布水平力,用于模拟横向地震作用下。墩柱高为 H,主梁跨径为 L。
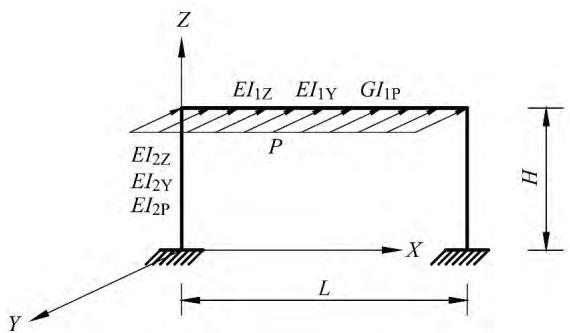
图 1 简化力学模型一
由于图 1 为对称结构,且作用荷载也是正对称的,故可取其一半作为基本体系进行计算,由于基本体系中反对称多余力为零,故最终可简化为如图 2 所示的基本体系。
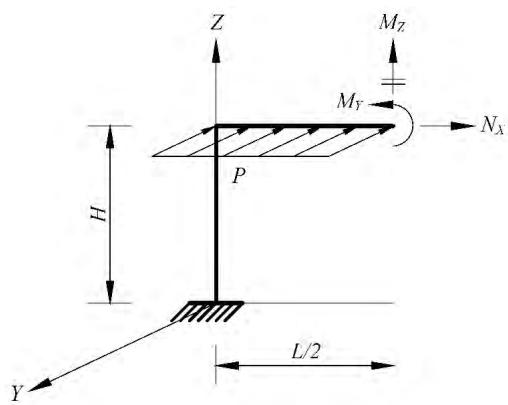
图 2 基本体系
由力法计算出多余力的结果为8:
最终,求得梁端的内力为:
梁端横向剪力:
梁端横向弯矩:
若墩柱的抗扭刚度记为 T = G I_{2P} / H,主梁截面横向抗弯刚度与柱抗扭刚度之比记为 \gamma = E I_{1Z} / T。
则梁端的横向弯矩即为墩柱的扭矩。由式(5)可以看出,墩梁固结时,在横向水平力作用下桥梁下部结构将会产生扭转效应,下部结构的扭矩大小与主梁截面横向抗弯刚度和墩柱抗扭刚度的比值有关,\gamma 越大,墩柱的扭矩值越小。由于实际工程中存在基础柔性的影响,故式(5)中墩柱的抗扭刚度应取为桥墩和基础组成的联合刚度,这里称其为墩柱的等效抗扭刚度。
2.2 模型二:设置支座力学模型
本文主要讨论不限制转动自由度的常规支座,一般分为四种类型:①双向固定支座;②纵向滑动,横向固定支座,简称横向固定支座;③横向滑动,纵向固定支座,简称纵向固定支座;④双向滑动支座。
通常桥梁在横向会布置两个或者两个以上支座,故本文采用具有代表性的横向布置两个支座作为单墩的支座布置形式。在横向水平荷载作用下,单墩横向布置的两个支座的纵向约束实际组成了一个限制梁端绕竖向转动的约束,这里将这个约束定义为 R_Z,其中,R_Z 的刚度为墩柱的抗扭刚度,梁的横向弯矩通过 R_Z 可以有效地传递到墩柱,使墩柱产生扭矩。而支座的横向约束(横向约束刚度为墩柱的横向抗推刚度)则实现了主梁横向剪力的有效传递。
表 1 中列出了实际桥梁工程中支座横向布置的常用组合及其约束的自由度。
表 1 支座组合
| 组合名称 | 支座组合 | 约束的自由度 |
|---|---|---|
| 固定墩 | 双向固定支座+纵向固定支座 | X, Y, Z, R_X, R_Z |
| 非固定墩 | 横向固定支座+双向滑动支座 | Y, Z, R_X |
注:X 为纵桥向平动,Y 为横桥向平动,Z 为竖向平动,R_X 为绕纵向的转动,R_Z 为绕竖向的转动。
从表 1 可以看出,实际桥梁工程中支座横向布置的常用组合中只有固定墩可以有效地将上部结构的横向弯矩传递给下部结构,使得下部结构产生扭转效应。
在纵桥向,由于需要适应上部结构在温度、徐变等因素影响下产生的的纵向变形,故一般不会在一跨的内设置两个固定墩,即在一跨内两个墩柱的支座布置是不对称的,通常为一个固定墩和一个非固定墩的组合方式。所以本文基于实际工程情况,选取最常用的支座布置形式,得到如图 3 所示的设置支座力学模型。
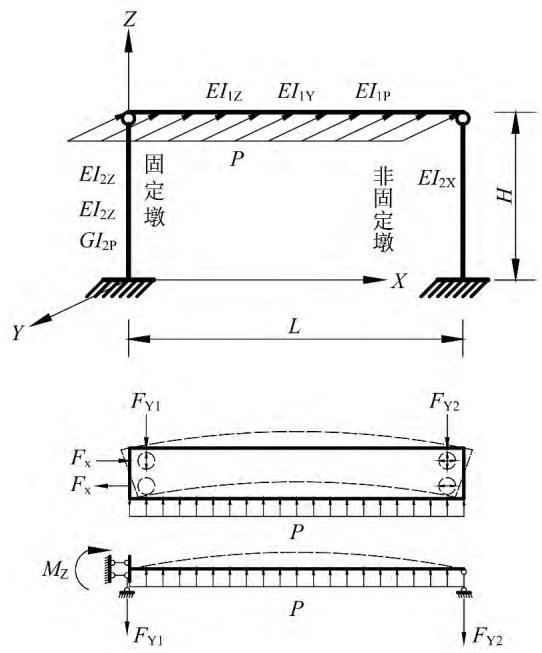
图 3 简化力学模型二
由力法求得其固定墩扭矩计算结果:
式中,K 为墩柱的横向抗推刚度,即 K = 3 E I_{2X} / H^3;\beta 为主梁截面横向抗弯刚度与墩柱横向抗推刚度之比,即 \beta = E I_{1X} / K。
由于实际工程中存在支座的抗剪刚度、基础柔性等影响,故公式(6)中墩柱的抗扭刚度和横向抗推刚度应取为支座、桥墩和基础组成的联合刚度,这里称其为墩柱的等效抗扭刚度和等效横向抗推刚度。
通过上述计算结果可以看出,模型二在横向地震作用下墩柱的扭转效应的影响因素有上部结构的横向抗弯刚度、支座布置形式、墩柱的等效抗扭刚度和墩柱的等效横向抗推刚度。当墩柱为固定墩时,在横向地震作用下,桥梁下部结构将会产生扭转效应,主梁的横向抗弯越小,墩柱产生的扭矩越大;墩柱的等效抗扭刚度和等效横向抗推刚度越大,墩柱产生的扭矩越大。从定性上可以得到这样的结论:对于大跨度桥梁,尤其是固定墩为矮粗墩的大跨度桥梁,在其固定墩处将会产生很大的扭转效应。通过模型一和模型二的分析结果可以看出,由于设置了支座,使得在扭转效应只产生在固定墩中。
3 实际桥梁工程的扭转效应分析
下面将通过一个桥梁工程实例的有限元模型分析支座、墩柱的等效抗扭刚度和墩柱的等效横向抗推刚度对桥梁下部结构扭转效应的影响。最后,通过 BCADPILE 软件,根据承台底部的内力反推在忽略扭矩和计入扭矩时最不利单桩的受力,进而分析扭转效应对桩基础的影响。
3.1 桥梁工程概况及模型介绍
春晓大桥主桥为 (80+336+80)\text{m} 中承式双层钢桁拱桥,上层为机动车道,下层为非机动车道;边、中跨跨度比为 0.24。主桁由两片钢桁架组成,桁宽 27.8\text{m},宽跨比为 1/12。主桥主墩( 10^\#、11^\#)墩高 3\text{m},截面直径 8 \sim 10\text{m},长细比小于 2.5,属于大直径矮墩。主桥在拱脚处设支座,10^\# 双柱墩为固定墩,其余墩柱为非固定墩。
图 4 为以春晓大桥为背景工程,由通用有限元软件 SAP2000 建立的三维有限元模型。参照实际结构的布置,上部结构中桥面主梁主要采用双主梁模式,程序中用梁单元模拟;钢横梁用梁单元模拟;混凝土桥面板用在系梁、横梁及小纵梁组成的梁格上布置的板单元模拟;整个拱圈(包括风撑)以及下部结构中的桥墩都是用梁单元模拟;吊杆与水平系杆用桁架单元模拟,承台也用梁单元模拟。桩基础的处理方法是在承台底部加上六个方向的弹簧来模拟桩基础的作用,弹簧刚度根据土层状况和桩的布置形式按静力等效的原则确定,其中土性资料一般根据 m 法确定。
地震动输入采用浙江省工程地震研究所提交的《宁波春晓大桥工程场地地震安全评价报告》提供的,所对应的反应谱曲线见图 5。
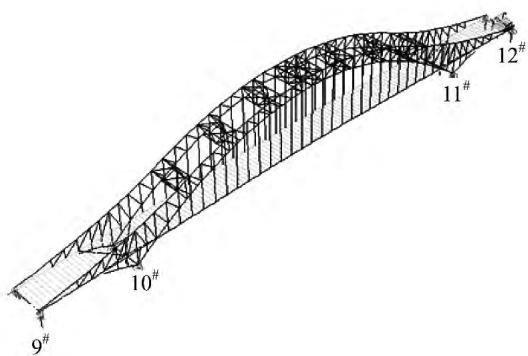
图 4 春晓大桥主桥动力计算模型图式
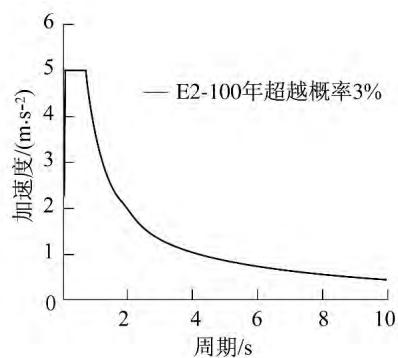
图 5 加速度反应谱曲线
3.2 支座对扭转效应的影响
表 2 为该桥在横向地震作用下由反应谱分析得到的承台底的内力最大值。从表中可以看出,设置支座时,10^\# 固定墩的承台底的扭矩值很大,约为横向弯矩的 0.6 倍,而其他非固定墩承台底的扭矩几乎为零。拱脚固结时,10^\# 主墩和 11^\# 主墩的承台底均产生很大的扭矩,而设置支座的非固定墩承台底的扭矩值也几乎为零。由于设置了支座,使得下部结构的扭转效应只在固定墩中产生,而非固定墩的支座布置形式,在横向地震作用中桥梁下部结构将不会产生扭转效应。
表 2 各承台底内力最大值
| 拱脚与桥墩连接方式 | 墩号 | 横向剪力 /\text{kN} | 横向弯矩/ (\text{kN}\cdot\text{m}) | 纵向弯矩/ (\text{kN}\cdot\text{m}) | 扭矩/ (\text{kN}\cdot\text{m}) |
|---|---|---|---|---|---|
| 设置支座 | 9^\# | 1.84\times 10^5 | 2.82\times 10^5 | 2.11\times 10^1 | 1.71 |
| 10^\# | 4.66\times 10^4 | 1.04\times 10^6 | 3.62\times 10^3 | 6.36\times 10^5 | |
| 11^\# | 4.67\times 10^4 | 1.03\times 10^6 | 3.22\times 10^1 | 6.87 | |
| 12^\# | 1.72\times 10^4 | 2.74\times 10^5 | 2.11\times 10^1 | 1.49 | |
| 拱脚固结 | 9^\# | 1.65\times 10^5 | 2.51\times 10^5 | 1.55\times 10^1 | 1.57 |
| 10^\# | 4.69\times 10^4 | 1.06\times 10^6 | 1.94\times 10^3 | 5.89\times 10^5 | |
| 11^\# | 4.73\times 10^4 | 1.07\times 10^6 | 2.19\times 10^3 | 5.93\times 10^5 | |
| 12^\# | 1.70\times 10^4 | 2.54\times 10^5 | 1.62\times 10^1 | 1.56 |
3.3 墩柱等效抗扭刚度对扭转效应的影响
在设置支座时,墩柱等效抗扭刚度为支座、桥墩和基础组成的联合刚度,当改变其中某一部分的抗扭刚度时,墩柱的等效抗扭刚度也会相应改变,且两者的关系是正相关的。由于梅山春晓大桥主桥主墩属于大直径矮墩,且和承台连接之后的整体的刚度很大,可以视为刚性构件。所以墩柱等效抗扭刚度对基础绕竖向转动刚度的改变更为敏感,故采用基础绕竖向转动刚度代替墩柱等效抗扭刚度进行分析。从图 6 可以看出,随着固定墩等效抗扭刚度的增加,固定墩承台底的扭矩也随之增大。
3.4 墩柱等效横向抗推刚度对扭转效应的影响
在设置支座时,墩柱等效横向抗推刚度为支座、桥墩和基础组成的联合刚度,基于上述同样的原因,这里同样采用基础横向刚度代替墩柱等效横向抗推刚度进行分析。从图 7 可以看出,随着固定墩等效横向抗推刚度的增加,固定墩承台底的扭矩也随之增大。
通过以上有限元模型分析的结果可以看出,基于简化力学模型分析得到的结论与对实际桥梁工程的扭转效应进行分析所得到的结论是一致的。
3.5 扭转效应对桩基础的影响
由表 2 可以看出,在横向地震作用下,固定墩处的承台底产生了很大的扭矩,而在桥梁抗震验算中,对桥梁基础地震反应进行验算时,一般只是根据承台底的弯矩、剪力、轴力来验算承台底单桩的抗弯和抗剪强度,而不计入扭矩的影响。但是并没有相关研究表明在抗震验算时忽略扭矩是否合理,故本文采用 BCADPILE 软件分别计算春晓大桥主桥固定墩在考虑扭矩和忽略扭矩时,最不利单桩的受力情况,得到结果如图 8 所示。通过对比可以发现,桥梁下部结构的扭转效应对于最不利单桩的受力有很大的影响,所以横向地震作用下桥梁下部结构产生很大扭转效应时,桥梁基础地震反应的验算应计入扭转效应的影响。
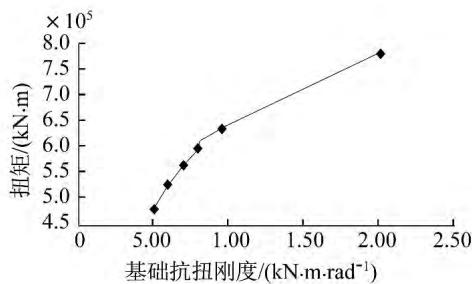
图 6 基础抗扭刚度对扭矩影响示意图
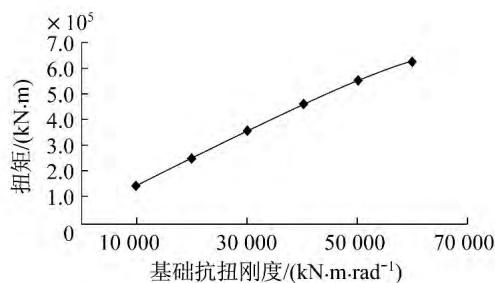
图 7 基础横向刚度对扭矩影响示意图
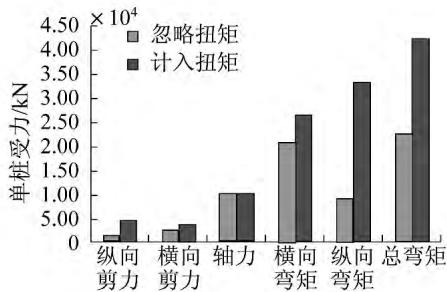
图 8 计入扭转效应和忽略扭转效应的最不利单桩受力比较
4 结论
本文通过简化的力学模型结合实际桥梁工程有限元分析模型,分析了桥梁结构在横向地震作用下,其下部结构扭转效应的影响因素。通过理论推导和实例分析,得到以下结论:
(1)对于墩梁固结体系,在横向地震作用下,桥梁下部结构将会产生扭转效应;对于设置支座体系,在横向地震作用下,在桥梁固定墩处将会产生扭转效应,而非固定墩,由于横向支座布置不能形成绕竖向转动的约束,故非固定墩处无扭转效应。
(2)横向地震作用下,上部结构的横向抗弯刚度越小,则桥梁下部结构的扭转效应越显著;墩柱等效抗扭刚度越大,桥梁下部结构的扭转效应越显著;墩柱等效横向抗推刚度越大,桥梁下部结构的扭转效应越显著。
(3)桥梁下部结构扭转效应很大时,将会对桩基础的受力产生较大的影响,在进行桥梁基础抗震验算时,应计入下部结构扭转效应的影响。
参考文献
黄小国, 敬大德, 宋小平. 桥墩扭转刚度对连续梁桥横桥向地震反应的影响 [J]. 结构工程师, 2008, 24(6):96-99. Huang Xiaoguo, Jing Dade, Song Xiaoping. The influence of piers torsion stiffness on the earthquake responses for continuous bridges in the transverse direction [J]. Structural Engineers, 2008, 24(6): 96-99. (in Chinese) ↩
中华人民共和国住房和城乡建设部. JTG/TB02—01—2008 公路桥梁抗震设计细则 [S]. 北京:中国建筑工业出版社,2008. Ministry of Housing and Urban-rural Development of the People's Republic of China. JTG/TB02-01-2008. Guidelines for seismic design of highway bridges [S]. Beijing: China Building Industry Press, 2008. (in Chinese) ↩
中华人民共和国住房和城乡建设部. CJJ166—2011 城市桥梁抗震设计规范 [S]. 北京:中国建筑工业出版社,2011. Ministry of Housing and Urban-rural Development of the People's Republic of China. CJJ 166—2011 Code for seismic design of urban bridge [S]. Beijing: China Building Industry Press, 2011. (in Chinese) ↩
扶长生. 抗震设计中的平扭耦联问题 [J]. 建筑结构学报, 2006, 27(2): 40-46. Fu Changsheng, Seismic design of torsionally coupled buildings [J]. Journal of Building Structures, 2006, 27 (2):40-46. (in Chinese) ↩
中华人民共和国建设部. GB 50011—2010 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2010. Ministry of Construction of the People's Republic of China. GB 50011—2010 Code for seismic design of buildings [S]. Beijing: China Architecture and Building Press, 2010. (in Chinese) ↩
中华人民共和国建设部. JGJ3—2010 高层建筑混凝土结构技术规程 [S]. 北京:中国建筑工业出版社,2010. Ministry of Construction of the People's Republic of China. JGJ 3—2010 Technical specification for concrete structures of tall building [S]. Beijing: China Architecture and Building Press, 2010. (in Chinese) ↩
叶爱君. 桥梁抗震 [M]. 2 版. 北京: 人民交通出版社, 2011. Ye Aijun. Seismic design of bridge [M]. Second Edition. Beijing: China Communication Press, 2011. (in Chinese) ↩
龙驭球, 包世华. 结构力学教程(I)[M]. 北京:高等教育出版社,2003. Long Yuqiu, Bao Shihua. Structural mechanics tutorial (I) [M]. Beijing: Higher Education Press, 2003. (in Chinese) ↩ ↩