刘腾飞,叶爱君,王晓伟
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:采用经过试验证的建模方法,建立了常规桩柱式简支梁桥的单墩数值计算模型,系统分析了土体约束作用对桩柱式桥墩整体延性性能、不同延性水平下桩身的曲率分布规律以及等效塑性铰长度的影响。结果表明:土体约束作用会显著增大桩柱式桥墩的截面破坏曲率,提高桥墩的水平承载力和位移延性系数,并显著减小桩身塑性区域长度和等效塑性铰长度,同时,桩身等效塑性铰长度还会随着位移延性系数的增大而显著减小。
关键词:桩柱式桥墩;基于性能的抗震设计;等效塑性铰长度;土体约束
中图分类号:U448.21 文献标志码:A
Confinement Effect of Soil on Plastic Hinge Length in Extended Pile-shafts
LIU Tengfei, YE Aijun, WANG Xiaowei
(State Key Laboratory of Disaster Reduction in Civil Engineering,
Tongji University, Shanghai 200092, China)
Abstract: Based on the calibrated numerical modeling method, a finite element (FE) model of the extended pile-shaft used in a simply supported bridge was developed. Then some FE models of extended pile-shafts embedded in sands varying different relative densities were established to study the confinement effect of soil on ① the displacement ductile capacity; ② the curvature distribution along the shafts and ③ the equivalent plastic hinge length of piles. The study indicates that confinement effect of soil can enhance the maximum sectional curvature of extended pile-shafts at failure significantly, increase both the lateral strength of piles and the displacement ductility factor, and lead to noticeable decrease of the plastic region length and the equivalent plastic hinge length of piles. The equivalent plastic hinge length of piles has a remarkable drop with the increase of the displacement ductility factor.
Key words: extended pile-shafts; performance-based seismic design; equivalent plastic hinge length; confinement effect of soil
桩柱式桥墩是一种桥墩结构深入到地下作为基础,桥墩和桩基础截面相同的特殊结构,由于不包含造价昂贵的承台,因而具有良好的经济性,在桥梁工程中得到了广泛应用。在地震荷载下,桩柱式桥墩的截面最大弯矩位于地面以下,因而土中部分不可避免地会产生塑性铰。国外桥梁抗震设计规范1,2,3也允许桩基础在特殊情况下进入塑性工作状态。
在基于性能的结构抗震设计4中,一个主要内容就是遵循“多级抗震”思想,建立多等级抗震性能指标体系以评估结构的抗震性能。具体到桥梁结构,如何确定不同性能水平下的结构验算指标是最重要的难题。对于桩柱式桥墩,一般采用位移延性系数来衡量桥墩在不同地震荷载水平下的损伤程度,采用墩顶位移作为抗震设计的验算指标,于是建立墩顶位移与不同位移延性系数之间的对应关系就成为基于性能的抗震设计中的一个重要问题。桩柱式桥墩的性能指标确定往往借鉴一般桥墩的方法5,6,即假定桩柱式桥墩可以等效为墩底固定的单墩模型,引入等效塑性铰长度的概念,推导出不同延性水平(位移延性系数)对应的墩顶位移。但是,由于桩柱式桥墩的塑性铰往往发生在地面以下,土体约束会对塑性区域的发生发展产生影响,故必须考虑土体约束对等效塑性铰长度的影响,此外基于性能的抗震设计思想还要求必须考虑不同延性水平下等效塑性铰长度的变化。
目前,国内外已有一些针对桩柱式桥墩等效塑性铰长度的研究。Chai 与 Hutchinson6,7,8通过对埋置于均一砂土(相对密实度 D_{\mathrm{r}} = 50\% , 85\% )中的桩柱式桥墩开展四组拟静力试验探求其非弹性性能,并通过桩顶位移反算等效塑性铰长度,试验得到了桩基的等效塑性铰长度对砂土密实度和位移延性系数都不敏感的结论,而 Budek 和 Priestley9为探求土体约束对于桩基塑性铰的影响,采用沿桩身一定范围布置若干作动器的方法模拟土体的外部约束,并通过比较 6 组试验结果,得到土的约束作用能增加桩基等效塑性铰长度的结论。另一方面,Budek 等人10分别利用线性、双线性和抛物线三种土体本构模拟桩土相互作用建立了用于分析不同自由段长度和土体初始刚度影响的桩柱式桥墩数值模型,研究其在均一砂土中的非弹性地震反应,并发现桩顶自由的桩柱式桥墩的等效塑性铰长度随土体刚度的增大而减小的结论;Zhang 等人11利用 p - y 曲线法模拟桩土相互作用,建立不同土体布置下桩柱式桥墩的有限元模型进行参数分析研究,并通过桩身曲率计算桩基位移延性系数为 3 时的等效塑性铰长度,数值分析结果表明土体刚度对桩基等效塑性铰长度有很大影响,等效塑性铰长度对土体条件是敏感的。可见,目前学界关于土体约束作用对桩基等效塑性铰长度影响仍存在分歧,而且之前的研究成果极少考虑桩基等效塑性铰长度随桩基延性水平的变化。因此,有必要对桩柱式桥墩等效塑性铰长度进行进一步的研究。
本文基于 OpenSees 平台,首先采用国外的试验结果对桩柱式桥墩有限元模型的建模方法进行验证,然后采用该建模方法,建立常规桩柱式墩公路桥梁的单墩数值模型,考虑不同土体约束作用的影响,分析土体约束作用对桩柱式桥墩整体延性性能的影响,然后深入分析不同土体约束作用和延性水平下桩身的曲率分布规律,最后分析总结土体约束作用和延性水平对桩柱式桥墩等效塑性铰长度的影响。
1 计算模型
为建立可靠的桩柱式桥墩数值模型进行弹塑性性能分析,首先采用美国的一个桩柱式桥墩试验的结果进行了建模方法的验证,然后采用同样的方法,以一座常规的桩柱式公路桥梁为背景,建立了考虑不同土体约束条件的一系列桩柱式桥墩计算模型。
1.1 建模方法及验证
Chai 和 Hutchinson6,7,8对加州常用的桩柱式桥墩基础(直径 D = 0.406\mathrm{m} )进行了一系列现场拟静力试验。重点研究了不同自由段长度和砂土相对密实度对于桩基非弹性性能的影响。本文基于 OpenSees 平台,建立试验试件 1 号桩(自由段长度 2D ,密砂)的有限元模型,并利用试验结果进行模型验证。
按文献6,7,8描述,试验在大尺寸盛土容器中进行。试件 1 号桩的桩径 D = 0.406\mathrm{m} ,土体埋深 13.5D ,桩底约束三个平动自由度,转动自由,砂土相对密实度 D_{\mathrm{r}} = 85\% ,内摩擦角 44^{\circ} ,土体有效重度 \gamma = 18\mathrm{kN}\cdot \mathrm{m}^{-3} ;桩顶自由,承受轴力 P = 445\mathrm{kN} (轴压比为 0.10);桩身截面保护层厚度 0.05\mathrm{m} ,保护层混凝土实际抗压强度 41\mathrm{MPa} ;纵向钢筋采用 7 根屈服强度 421\mathrm{MPa} 的 A706 \Phi 22 钢筋,箍筋采用屈服强度 710\mathrm{MPa} 的 MW25 的螺旋箍筋,箍筋间距为 50~\mathrm{mm} 。
在 OpenSees 平台,基于非线性 Winkler 地基梁方法,建立试件 1 号桩有限元模型:桩基采用非线性纤维截面单元模拟,自由段划分为 2 个 1.0D 的单元,土下埋深 6D 以内部分划分为 12 个 0.5D 单元, 6D 以下部分划分为 3 个 1.0D 单元和 3 个 1.5D 单元,单个纤维截面划分为 72 根核心混凝土纤维、24 根保护层混凝土纤维和 7 根纵向钢筋纤维,见图 1。
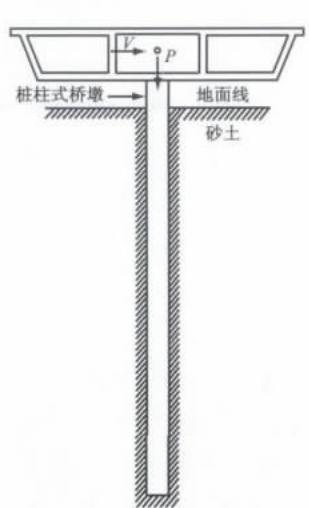
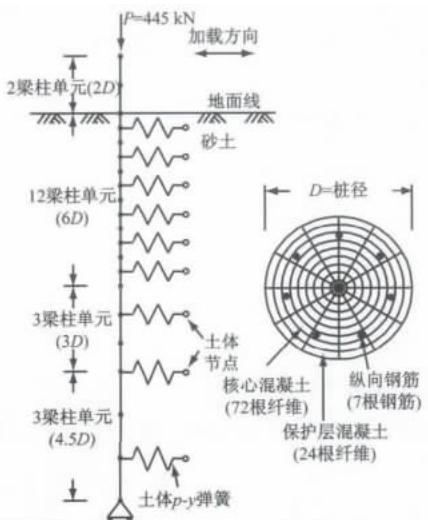
图 1 有限元模型图示
Fig.1 General schematic of the FE model
本文采用 Kent-Park 模型12模拟混凝土材料本构,其中核心混凝土极限应变采用 Mander13提供的公式计算,如图 2a 所示。纵向钢筋采用双线性本构,如图 2b 所示,屈后刚度比为 0.0097 。利用 API 规范14中砂土 p - y 曲线,如图 2c 所示,考虑桩土相互作用,计算方式如下:
式中, p 为土体表面以下深度 \textbf{z} 处单位桩长的水平土抗力; y 为此深度处桩身的水平位移; p_{\mathrm{u}} 为地面以下深度 \textbf{z} 处单位桩长的极限水平土抗力。根据式(2)求解,联立该式可得浅层土与深层土的临界深度 \mathcal{Z}_{\mathrm{r}} 。 C_1,C_2 和 C_3 为系数,取值按照 API 规范确定。其中, D 为桩径; \gamma 为土体有效重度; A 为荷载类型系数,按照式 (3) 确定; n_{\mathrm{h}} 为地基模量系数。
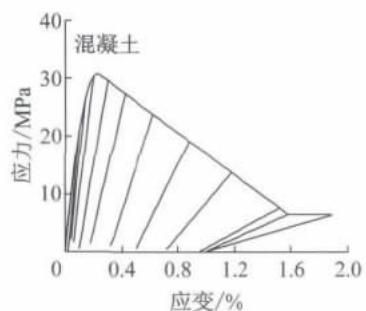
a 混凝土本构曲线
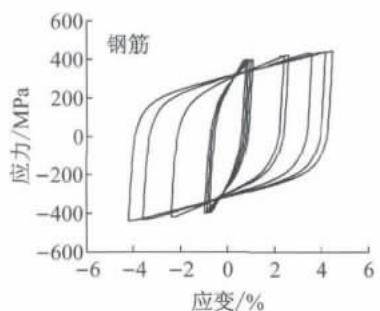
b 钢筋本构曲线
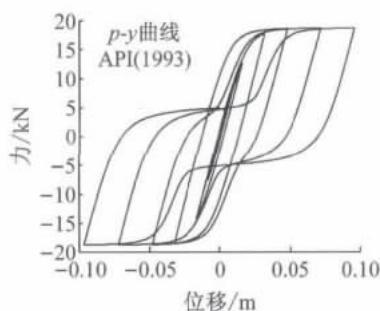
c 埋深 0.5D 处 p - y 弹簧滞回曲线
图 2 材料滞回特性
Fig.2 Material cyclic behavior
根据文献7,15,16,17的研究,API 规范作为工程设计规范过于保守,给出的 p - y 曲线过高估计了砂土初始刚度 K_{\mathrm{in}} = n_{\mathrm{h}}z ,并低估了土体极限抗力 p_{\mathrm{u}} ,实测的桩周土体 p - y 曲线更接近双曲线型。因而在利用 API 规范 p - y 曲线法进行试验数据数值模拟时需对砂土初始刚度 K_{\mathrm{in}} (通过修正 n_{\mathrm{h}} 实现)和土体极限抗力 p_{\mathrm{u}} 进行必要的修正。但是由于桩周土是一种复杂弹塑性介质,桩土相互作用是一个复杂的三维问题,现有研究并未得出统一的修正方法,而且侧向位移下不同埋深处土体位移不同, p - y 弹簧的修正系数必然会有差异。本文偏简便地对所有 p - y 弹簧采用相同的修正系数进行修正,具体而言: n_{\mathrm{h}} 值采用与实测值6更接近的 ATC-3218推荐值,如图 3 所示, n_{\mathrm{h}} 值可根据砂土相对密实度选取。根据文献7,16,17的研究,同时也考虑到土体性质的不确定性,本文分别对 p - y 弹簧的土体极限抗力 p_{\mathrm{u}} 和初始刚度 K_{\mathrm{in}} 乘以 3.5 和 0.85 的修正系数。
通过在有限元模型的桩顶施加位移控制的循环往复荷载进行推倒分析。试验以及有限元分析得到的力 - 位移滞回曲线和骨架曲线如图 4 所示,可见有限元结果与试验数据吻合良好,证明了本文采用的数值分析方法是可靠的。
1.2 桩柱式桥墩计算模型
利用上述验证过的建模方法,以一座 3 \times 30 \mathrm{~m} 的三跨简支桩柱式梁桥为背景,建立了实际桥梁的桩柱式桥墩模型,如图 5 所示。其中,桩柱式桥墩的桩底固定,桩顶自由;桩径 D = 1.5\mathrm{m} ,桩基埋深 12D = 18\mathrm{m} ,自由段长度 4D = 6.0\mathrm{m} ,总长 16D = 24.0\mathrm{m} ;桩身采用 C40 混凝土,保护层厚度 80~\mathrm{mm} ;纵向钢筋采用 36 根 HRB400 \Phi 28 钢筋,对应的纵向配筋率为 1.2\% ;箍筋采用 HRB400 \Phi 32 螺旋钢筋,间距 150~\mathrm{mm} ,体积配箍率为 0.8\% ;轴向压力 P = 1890\mathrm{kN} (对应的轴压比为 0.05);桩身位于密实干砂中,相对密实度 D_{\mathrm{r}} = 50\% ,内摩擦角为 33^{\circ} ,土体
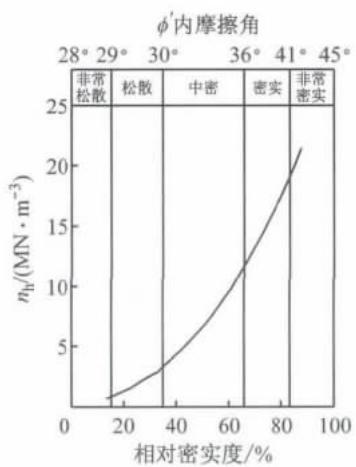
图 3 ATC-32 的 n_{\mathrm{h}} 推荐值
Fig. 3 Recommendation value of n_{\mathrm{h}} from ATC-32
有效重度为 17\mathrm{kN}\cdot \mathrm{m}^{-3} 。
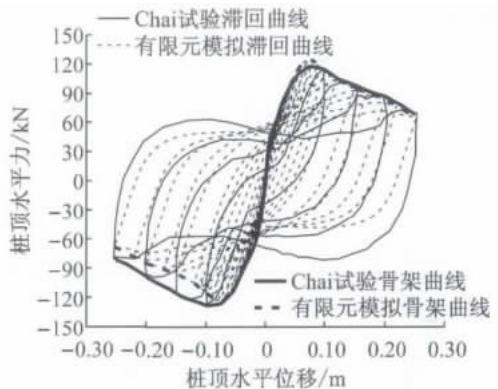
图 4 桩 1 试验与有限元分析结果比较
Fig. 4 Comparison of the measured and FE calculated hysteretic response of pile 1
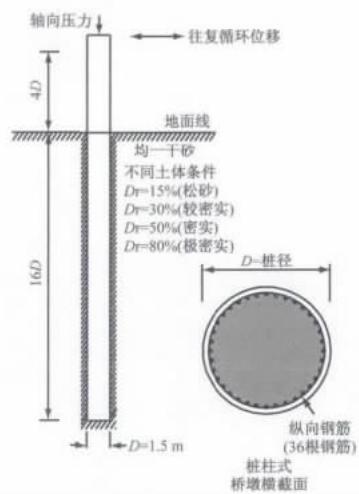
图 5 桩柱式桥墩布置图
Fig. 5 Configuration of the extended pile-shaft
在 OpenSees 有限元模型中,桩身单元采用非线性纤维截面单元模拟,自由段划分为 4 个 1.0D 的单元,土体埋深 6D 以内部分划分为 12 个 0.5D 单元, 6D 以下部分划分为 4 个 1.5D 单元,单个纤维截面划分为 468 根纤维,包括 396 根核心混凝土纤维,36 根保护层混凝土纤维和 36 根纵向钢筋纤维。材料特性(图 2)模拟方法与之前验证的有限元模型一致。
在此模型基础上,通过改变土体相对密实度 D_{\mathrm{r}} (15\% , 30\% , 50\% 和 80\%) 和不考虑土体约束,建立了一系列的桩柱式桥墩数值模型,用以研究土体约束作用对桩柱式桥墩塑性性能的影响。
2 土体约束对桩柱式桥墩整体延性性能的影响
为了研究土体约束作用对桩柱式桥墩弹塑性性能的影响,对所建立的一系列对应于不同土体密实度的有限元模型,进行了推倒分析。
图 6 给出了推倒分析后得到的 4 个桩柱式桥墩模型 (D_{\mathrm{r}} = 15\% , 30\% , 50\% 和 80\%) 和不考虑土体约束的无土模型的骨架曲线。其中,破坏状态定义为桩基某一截面达到由截面弯矩一曲率分析确定的极限曲率(控制条件为核心混凝土达到极限压应变,或钢筋达到极限拉应变,达到二者之一即可),桩基水平承载力下降到水平承载力峰值的 85\% ,只要达到其中之一即为破坏;首次屈服点对应于桩身截面钢筋首次屈服;等效屈服点对应的是现有规范中采用理想双线性模型模拟力和位移关系、基于能量相等原则得到的屈服点。
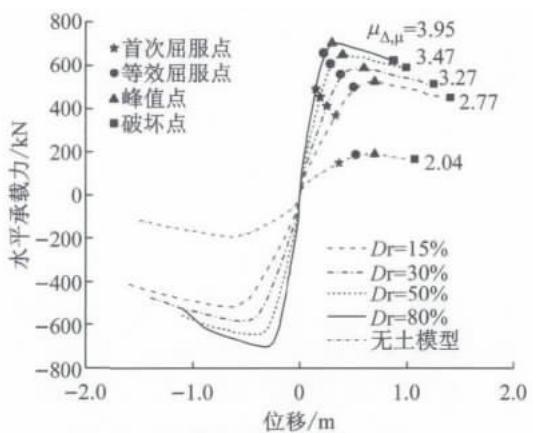
图 6 不同土体约束下骨架曲线比较
Fig. 6 Comparison of skeleton curves of FE models in different soil condition
从图 6 中可以发现:随着土体刚度的增加,初始刚度单调增大,峰值点位移逐渐减小,峰值点强度逐渐提高;而且除峰值点外,其余表征不同模型塑性发展过程的几个关键点,包括首次屈服点、等效屈服点和破坏点时对应的承载力和位移随土体刚度变化的规律和峰值点处保持一致,即 D_{\mathrm{r}} 增大引起模型各关键点处对应的位移变小,强度提高。但是,随着土体刚度的增加,桩柱式桥墩破坏时的位移延性系数单调增大。
表 1 给出了不同土体约束下桩柱式桥墩的主要性能指标,结果表明,砂土密实度从 15% 提高到 80% ,屈服力增大了 32% ,屈服位移减小了 56% ,极限位移减小了 37% ,位移延性系数则增大了 43% 。
可见,随着土体约束作用的增大,桩柱式桥墩的刚度逐渐增大,桥墩的水平承载能力逐渐增大,桥墩的屈服位移和破坏位移逐渐减小,但位移延性系数反而逐渐增大。因此,从桩柱式桥墩的屈服破坏全过程来看,土体约束对桩柱式桥墩的整体延性性能有显著的影响。
表 1 不同土体约束下桩柱式墩的性能指标
Tab. 1 Performance indexes of extended pile-shafts in different soil conditions
| 关键点 | 力学指标 | 无土模型 | Dr=15% | Dr=30% | Dr=50% | Dr=80% |
|---|---|---|---|---|---|---|
| 等效屈服点 | 位移/m | 0.525 | 0.505 | 0.381 | 0.286 | 0.222 |
| 承载力/kN | 190.01 | 499.09 | 558.26 | 610.61 | 658.98 | |
| 破坏点 | 位移/m | 1.072 | 1.400 | 1.244 | 0.991 | 0.877 |
| 位移延性系数 | 2.04 | 2.77 | 3.27 | 3.47 | 3.95 | |
| 承载力/kN | 168.84 | 452.27 | 513.85 | 590.60 | 625.98 |
3 土体约束对桩柱式桥墩局部损伤的影响
图 7a 给出了在不同的土体约束作用下,桩柱式桥墩达到破坏状态时对应的桩身曲率分布,从图中可以看出,与普通桥墩相比,桩柱式桥墩的曲率分布图有本质的区别,这是土体约束作用造成的。普通桥墩的截面最大曲率发生在墩底,而桩柱式桥墩的截面最大曲率位于地表以下一定埋深处。此外,随着砂土密实度的增大,土体约束作用逐渐增大,桩身最大截面曲率逐渐增大,对应的埋深则逐渐减小,而且桩身塑性曲率分布也越集中,从而减小了桩身塑性区域长度,对应的等效塑性铰长度也会相应减小。
图 7b 画出了不同桩柱式桥墩位移延性系数对应的桩身曲率分布图,可见,随着延性水平的增加,截面最大曲率逐渐增大,对应的埋深逐渐变小,而曲率分布的尖峰特性更加显著,塑性区域的变化则不明显。
进一步地,表 2 对不同土体约束下,桩身截面的屈服曲率和破坏曲率及桩身截面最大曲率位置进行了比较。其中,屈服曲率为桩首次屈服时沿桩身的最大截面曲率,破坏曲率为桩达到破坏状态时沿桩身的最大截面曲率,如图 7b 所示。结果表明,砂土密实度从 15% 提高到 80% ,屈服曲率减小了 5.3% ,但破坏曲率增大了 25% ,曲率延性系数增大了 32% ,屈服曲率对应的埋深从 3.83D 减小到 1.5D ,破坏曲率对应的埋深从 3.33D 减小到 1.5D ,分别减小了 61% 和 55% 。值得注意的是,密实度大于 50% 后,桩柱式墩的各项性能指标就变化不大了。
表 2 不同土体约束下桩身截面曲率
Tab. 2 Details of sectional curvature of extended pile-shafts in different soil conditions
| 不同模型 | 屈服曲率 φy/m-1 | 屈服曲率 埋深 | 破坏曲率 φu/m-1 | 破坏曲率 埋深 | 曲率延性 系数 μφ |
|---|---|---|---|---|---|
| 无土模型 | 0.003 053 | - | 0.011 667 | - | 3.82 |
| Dr=15% | 0.003 445 | 3.83D | 0.045 985 | 3.33D | 13.35 |
| Dr=30% | 0.003 387 | 3.33D | 0.052 133 | 2.33D | 15.39 |
| Dr=50% | 0.003 307 | 2.5D | 0.057 451 | 1.5D | 17.37 |
| Dr=80% | 0.003 263 | 1.5D | 0.057 398 | 1.5D | 17.59 |
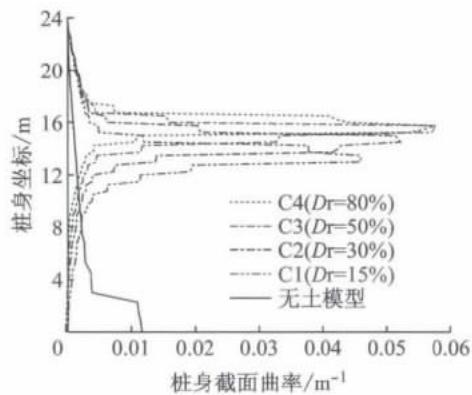
a 破坏状态的桩身曲率分布
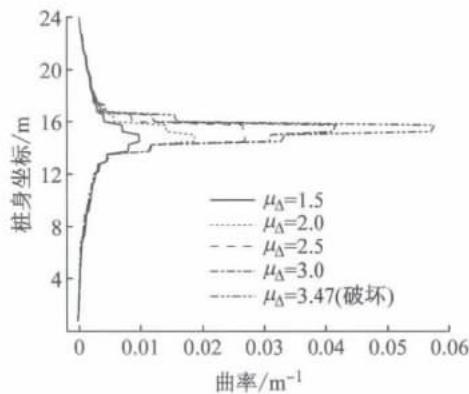
b D_{\mathrm{r}} = 50\% 时桩身曲率分布
图 7 桩身截面曲率分布
Fig. 7 Sectional curvature distribution along pile shafts
因此,土体的约束作用会使桩柱式桥墩的截面破坏曲率显著增大,曲率延性系数显著增大,但约束作用达到一定程度( D_{\mathrm{r}} > 50\% )之后,这种影响就不明显了,这和箍筋的约束作用非常相似。
4 土体约束对于桩柱式桥墩塑性铰长度的影响
为进一步研究土体约束作用对于桩身塑性铰长度的影响,计算了 D_{\mathrm{r}} 分别为 15\% , 30\% , 50\% 和 80\% 时对应工况的桩身塑性区域长度和等效塑性铰长度值 L_{\mathrm{p}} 。其中,塑性区域长度为桩身进入塑性(截面曲率大于屈服曲率 ) 的部分的长度。
L_{\mathrm{p}} 计算方法14为
其中, \theta_{\mathrm{p}} 为桩的塑性转角; \phi_{\mathrm{p}} 为桩的最大截面塑性曲率。塑性转角通过对沿桩身各积分点的塑性曲率进行积分得到,如图 8 所示。
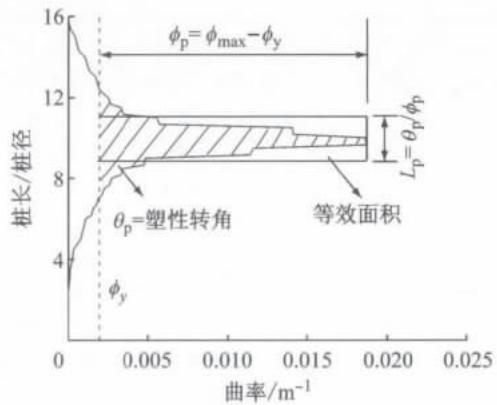
图 8 等效塑性铰长度方法
Fig. 8 Strategy for calculating the equivalent plastic hinge length
表 3 给出了不同土体约束下,桩柱式桥墩塑性区域长度和等效塑性铰长度随位移延性系数变化(从等效屈服状态直至破坏状态)的情况。
从表 3 结果可见,随着砂土密实度 D_{\mathrm{r}} 的增大,桩身的塑性区域长度明显减小,砂土密实度从 15% 增大到 80% ,破坏时塑性区域长度从 7.6D 变为 5.24D ,减小了 31% ;对于同一 D_{\mathrm{r}} ,随着延性水平的增大,塑性区域长度稍有增加,但增幅仅为 3.6\% \sim 9.2\% ,基本可忽略。
表 3 不同位移延性水平下各模型中塑性铰长度
Tab. 3 Plastic hinge length of FE models at different displacement ductility levels
| 塑性铰长度 | Dr | μΔ=1.5 | μΔ=2.0 | μΔ=2.5 | μΔ=3.0 | 破坏 |
|---|---|---|---|---|---|---|
| 塑性区 域长度 | 15% | 7.25D | 7.50D | 7.56D | - | 7.60D |
| 30% | 6.14D | 6.23D | 6.28D | 6.32D | 6.36D | |
| 50% | 5.33D | 5.49D | 5.58D | 5.66D | 5.79D | |
| 80% | 4.80D | 4.97D | 5.09D | 5.17D | 5.24D | |
| 等效塑性 铰长度 Lp | 15% | 2.35D | 1.72D | 1.41D | - | 1.48D |
| 30% | 2.13D | 1.50D | 1.42D | 1.42D | 1.35D | |
| 50% | 1.77D | 1.48D | 1.46D | 1.21D | 1.06D | |
| 80% | 1.53D | 1.23D | 1.01D | 1.03D | 1.02D |
表 3 结果同时表明,砂土密实度和延性水平都对桩身等效塑性铰长度有显著影响。总体而言,随着 D_{\mathrm{r}} 增大,桩身等效塑性铰长度显著下降,砂土密实度从 15% 增大到 80% ,破坏时等效塑性铰长度从 1.48D 变为 1.02D,减小了 31% ;对于同一 D_{\mathrm{r}} ,随着位移延性系数 \mu_{\Delta} 的不断增加,等效塑性铰长度 L_{\mathrm{p}} 也表现为总体减小趋势,从延性系数 1.5 到破坏,等效塑性铰长度的降幅为 33\% \sim 40\% 。
5 结论
针对桩柱式桥墩基于性能的抗震设计中,简化计算桥墩位移能力所需要解决的等效塑性铰长度的问题开展了研究。采用经过试验验证的建模方法,建立了常规桩柱式墩公路桥梁的单墩数值计算模型,考虑不同的土体参数,进行了一系列的推倒分析,分析了土体约束作用对桩柱式墩的整体延性性能,局部损伤指标以及等效塑性铰长度的影响,得到了以下结论:
(1)土体约束作用对桩柱式桥墩的整体延性性能有显著的影响,会显著减小桥墩的屈服位移和破坏位移,但会显著提高桥墩的水平承载能力和位移延性系数。
(2) 土体约束作用会使桩柱式桥墩的截面破坏曲率和曲率延性系数显著增大, 但约束作用达到一定程度 ( 密实度 D_{\mathrm{r}} > 50\% ) 之后, 这种影响就不再明显。
(3)土体约束作用会使桩柱式桥墩的塑性区域长度和等效塑性铰长度显著减小。
(4)延性水平对桩柱式桥墩塑性区域长度的影响可以忽略,但随着位移延性系数的增大,桩身等效塑性铰长度会显著减小,在基于性能的抗震设计中应予以考虑。
参考文献:
American Association of State Highway and Transportation Officials. AASHTO guide specifications for LRFD seismic bridge design[S]. 2nd ed. Washington D C: AASHTO, 2011. ↩
California Department of Transportation (Caltrans). Seismic design criteria[S]. Sacramento: Caltrans, 2011. ↩
日本道路协会. 道路桥示方书. 同解说 [S]. 东京: 丸善株式会社, 2011. Japan Road Association. Design specification of Japan highway bridge (explanation)[S]. Tokyo: Maruzen Ltd, 2011. ↩
SEAOC Vision 2000 Committee. Performance-based seismic engineering structural engineers association of California[S]. Sacramento: SEAOC Vision 2000 Committee, 1995. ↩
Dowrick D J. Earthquake resistant design [M]. 2nd ed. New York: Wiley-Interscience, 1987. ↩
Chai Y H, Hutchinson T C. Flexural strength and ductility of reinforced concrete bridge piles [R]. Davis: University of California, 1999. ↩ ↩ ↩ ↩ ↩
Hutchinson T C, Boulanger R W, Chai Y H, et al. Inelastic seismic response of extended pile shaft supported bridge structures [R]. Berkeley: Pacific Earthquake Engineering Research Center, University of California, Berkeley, 2002. ↩ ↩ ↩ ↩ ↩ ↩
Chai Y H, Hutchinson T C. Flexural strength and ductility of extended pile-shafts. II: experimental study[J]. Journal of Structural Engineering, 2002, 128(5): 595. ↩ ↩ ↩
Budek A M, Priestley M J N, Benzoni G. The effect of external confinement on flexural hinging in drilled pile shafts [J]. Earthquake Spectra, 2004, 20(1): 1. ↩
Budek A M, Priestley M J N, Benzoni G. Inelastic seismic response of bridge drilled-shaft RC pile/columns[J]. Journal of Structural Engineering, 2000, 126(4): 510. ↩
Zhang J, Hutchinson T C. Inelastic pile behavior with and without liquefaction effects[J]. Soil Dynamics and Earthquake Engineering, 2012, 36(3): 12. ↩
Kent DC, Park R. Flexural members with confined concrete [J]. Journal of Structural Division, 1971, 97(7): 1964. ↩
Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Division, 1988, 114(8):1804. ↩
American Petroleum Institute. API RP2A-WSD Recommended practice for planning, designing and constructing fixed offshore platforms—working stress design [S]. Washington DC: American Petroleum Institution, 1993. ↩ ↩
Yan L, Byrne P M. Lateral pile response to monotonic pile head loading [J]. Canadian Geotechnical Journal, 1992, 29 (6): 955. ↩
Allotey N, El Naggar M H. A numerical study into lateral cyclic nonlinear soil-pile response[J]. Canadian Geotechnical Journal, 2008, 45(9): 1268. ↩ ↩
朱斌, 朱瑞燕, 罗军, 等. 海洋高桩基础水平大变位性状模型试验研究 [J]. 岩土工程学报, 2010, 32(4): 521.
ZHU Bin, ZHU Ruiyan, LUO Jun, et al. Model tests on characteristics of ocean and offshore elevated piles with large lateral deflection [J]. Chinese Journal of Geotechnical Engineering, 2010, 32(4):521. ↩ ↩Applied Technology Council (ATC). Improved seismic design criteria for California bridges: provisional recommendations [R]. Redwood City: Applied Technology Council, 1996. ↩