韩振峰1, 叶爱君2
(1. 合肥学院建筑工程系,安徽合肥 230601;2. 同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:针对漂浮型的千米级斜拉桥,研究地震作用下减小梁端纵向位移和主塔内力的方法。首先阐述了该类桥梁的纵向减震机理和方法;其次根据现有的理论和技术水平,在塔梁之间分别采用弹性连接装置、流体黏滞阻尼器、以及弹性连接装置与流体黏滞阻尼器组合的 3 种连接方式,设计了 3 种纵向减震体系;然后建立了千米级斜拉桥的有限元模型,分别采用上述 3 种纵向减震体系,进行了一系列动力分析,同时研究了纵向减震参数设置;最后,对模型计算结果进行了比较和讨论,并建议了千米级斜拉桥纵桥向的合理减震结构体系。
关键词: 千米级斜拉桥; 纵向减震; 弹性连接装置; 黏滞阻尼器; 梁端位移
中图分类号:U448
文献标志码:A
Research on the longitudinal earthquake-reduction system of cable-stayed bridges over kilometers
HAN Zhenfeng ^{1} , YE Aijun ^{2}
(1. Department of Architectural Engineering of Hefei University, Hefei 230601, China;
- State Key Laboratory for Disaster Reduction of Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: For the floating system cable stayed bridges (CSBs) over one kilometer, exploring the methods to reduce the longitudinal displacements at beam end and the internal forces in the tower under earthquake action. Firstly, elaborating the longitudinal earthquake-reduction mechanism and method of the long span CSBs over one kilometer. Secondly, using the elastic connecting device, liquid viscous damper, and the combination of former two, between the tower and beam, build three longitudinal earthquake-reduction systems base on the current theory and technology achievement of bridge engineering. Thirdly, a finite element model of this type CSBs is set up using the above three longitudinal earthquake-reduction systems and several dynamic analyses are performed. Also, the parameters of longitudinal earthquake-reduction are set. Lastly, comparing and discussing the compute results of the model, and recommending the rational longitudinal earthquake-reduction system of this type CSBs.
Key words: cable-stayed bridge; earthquake-reduction; elastic connecting device; viscous damper; beam end displacement
引言
近年来,我国斜拉桥的发展迅速,以其经济性和多变性的优势,跨度已超越千米。由于大跨度斜拉桥的主塔很高,延性性能不好,而且一旦塔根出现塑性铰,塔顶将产生较大的残余变位,震后修复比较困难,因此,目前普遍认同大跨度斜拉桥在设计地震下保持弹性。大跨度斜拉桥的抗震对策只能是设法减小桥梁结构的地震反应,采用减隔震技术1,2,3。
千米级的超大跨度斜拉桥,由于超常规的跨度和柔性,其地震反应特性与 500\mathrm{m} 左右的大跨度斜拉桥有一些不同,地震易损性也不一样,其抗震策略虽然也是要设法减小地震反应,但具体方法上有所不同4。
论文首先阐述了千米级斜拉桥的减震机理和方法,重点强调了纵向减震机理和方法;然后在塔梁之间分别采用弹性连接装置、流体黏滞阻尼器、以及弹性连接装置与流体黏滞阻尼器组合的 3 种连接方式,设计了 3 种纵向减震体系;其次建立了千米级斜拉桥的有限元模型,分别采用了上述 3 种纵向减震体系,进行了一系列动力分析,并且研究纵向减震参数设置;最后对模型计算结果进行了讨论,并建议了千米级斜拉桥纵桥向的合理减震结构体系。
1 减震机理和方法 7,8
减隔震技术是利用结构地震反应的基本规律,一方面,引入柔性装置来延长结构的基本周期,以避开地震能量集中的周期范围,降低结构地震力;另一方面,在结构中引入阻尼装置,增加结构阻尼,耗散地震能量,减小结构位移。在斜拉桥的纵桥向,飘浮体系是一种对抗震有利的结构体系。从某种意义上说,飘浮体系可以看成是一种隔震体系,它通过延长结构周期来减小地震内力。但对于千米级斜拉桥,如果仍然采用飘浮体系减小地震内力,则会由于结构的纵飘周期太长、结构阻尼低,导致梁端产生过大的地震位移。
采用飘浮体系的千米级斜拉桥要减小梁端的位移反应,有两种途径:(1)适当增大结构的刚度,缩短结构周期,兼顾力和位移。增大结构刚度的方法有两种,1)增大主塔的纵向刚度;2)在上下部结构之间增设连接装置。(2)增大桥梁结构的阻尼,增大结构阻尼的最有效方法是在上下部结构之间增设阻尼装置。
2 纵向减震体系
在国内外已建成的大跨度斜拉桥中,纵向结构体系主要有 3 类:(1)飘浮体系;(2) 塔梁纵向刚性约束体系;(3) 飘浮体系和纵向约束装置的组合体系。对于千米级斜拉桥,飘浮体系和塔梁纵向刚性约束体系都存在缺陷。
从静力反应来看,飘浮体系会导致梁端和塔顶的纵向位移很大,而且纵向静风力和制动力产生的塔底弯矩也很大;而塔梁纵向刚性约束体系能大大减小梁端和塔顶的纵向位移,但由温度变化引起的主梁轴力和塔底弯矩又很大。从地震反应来看,采用飘浮体系,主塔的内力反应较小,但梁端、塔顶纵向位 4 移大;而塔梁纵向刚性约束体系能减小梁端、塔顶位移,但会增加主塔内力。
因此,如果在塔梁之间增设一定的纵向约束装置,则能改善斜拉桥的静力、动力性能。塔梁之间的连接方式有较多的选择。论文在塔梁之间分别采用:(1)弹性连接装置;(2)流体黏滞阻尼器;(3)弹性连接装置与流体黏滞阻尼器组合 3 种方式,建立了 3 种不同的纵向减震体系。
3 减震装置
3.1 弹性连接装置
弹性连接装置的作用是提供弹性刚度,主要有大型橡胶支座、钢铰线拉索以及用于限位的液压缓冲装置。由于弹性连接装置的刚度对各种荷载均起作用,因此为了协调各种荷载下结构的性能,在选定弹性约束装置的刚度时,除了考虑抗震的需要外,还应兼顾结构在温度、活载、风荷载等荷载作用下的反应。
3.2 流体黏滞阻尼装置
流体黏滞阻尼器的阻尼力 F 与速度 V 之间的关系理论上可以表示为:
其中, C 是通过试验确定的阻尼系数, \alpha 指数表征流体黏滞阻尼器的非线性特性, \mathrm{sgn}(\cdot) 是正负号函数。
线性阻尼器的恢复力特性如图 1 所示,从中可以看出:在结构达到最大变形时,阻尼器的阻尼力反而最小, 接近于零; 而阻尼器的阻尼力最大时, 结构变形最小, 弹性力也最小。线性阻尼器的阻尼力和结构的弹性力之间有 90^{\circ} 的相位差, 不增加结构的受力。液压黏滞阻尼器对慢速位移 (温度、活载、风荷载等引起) 不起约束作用, 仅对地震、脉动风和车辆振动引起的动力反应提供耗能减震作用。
4 模型的建立
4.1 模型描述
斜拉桥的跨径布置为 2 \times 100 \mathrm{~m} + 300 \mathrm{~m} + 1088 \mathrm{~m} + 300 \mathrm{~m} + 2 \times 100 \mathrm{~m} 、全长 2088 \mathrm{~m} 七跨连续钢箱梁双塔斜拉桥,见图 2。采用倒 Y 形钢筋混凝土索塔,塔高 297.7 \mathrm{~m} ,其中上塔柱为锚索区塔柱,中、下塔柱为两个分离的倾斜塔柱,在锚索区底部合为一体,桥面下设下横梁。下横梁上不设支座。索塔基础采用哑铃型变厚度承台和 131 根 \mathrm{D}2.8 \mathrm{~m} / \mathrm{D}2.5 \mathrm{~m} 变直径钻孔灌注桩基础。边墩包括近塔辅助墩、远塔辅助墩和过渡墩,墩顶设纵向滑动球型钢支座。
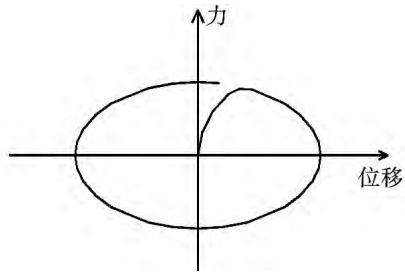
图 1 黏滞阻尼器的滞回曲线
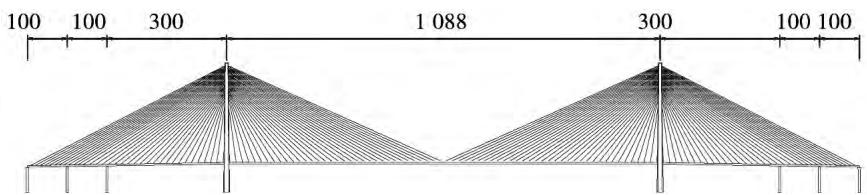
Fig. 1 Hysteresic curve of the viscous damper
Fig.2 Longitudinal profile of the model 1
图 2 模型 1 立面图(单位:m)
建模细节:在 ADINA 软件中建立三维有限元力学模型进行动力非线性反应研究。其中,主梁、塔、边墩用梁单元模拟,主梁节点和斜拉索吊点用刚臂相连;斜拉索用桁架单元模拟;主梁与主塔纵向之间设置连接单元(模拟减震装置),横向主从;主梁与边墩纵向相对自由,横向主从;见图 3。
由于论文研究重点在上部桥跨结构,故在墩底(承台顶)采取固结处理,另外,拉索的局部振动不控制设计,不作为研究对象。
4.2 模型的动力特性
对于索类结构,恒载几何刚度对超大跨度斜拉桥的动力特性会产生影响,先将恒载产生的轴向力转化为几何刚度,分别对应于索、主塔、墩、梁的几何刚度,然后在考虑了这些恒载几何刚度后的斜拉桥结构上进行模态分析,得到所需的动力特性结果,如表 1 所示。

图 3 三维有限元模型
Fig. 3 3D Finite element model
Table 1 Dynamic properties of the model
表 1 模型的动力特性
| 阶数 | 振型特征 | 频率(Hz) |
|---|---|---|
| 1 | 纵飘 | 0.0656 |
| 2 | 中跨对称侧弯 | 0.1004 |
| 3 | 1阶对称竖弯 | 0.1779 |
| 4 | 1阶反对称竖弯 | 0.2195 |
| 5 | 中跨反对称侧弯 | 0.2819 |
| 6 | 塔对称侧弯 | 0.3083 |
| 7 | 塔反对称侧弯 | 0.3718 |
| 8 | 1阶对称扭转 | 0.9948 |
| 9 | 1阶反对称扭转 | 1.7067 |
5 分析方法及参数选择 12,13,14,15,16
5.1 分析方法
一个具有 n 个自由度的桥梁结构,附加流体黏滞阻尼器设置在 n_{l} 个不同的位置上,其地震振动方程如式(2)所示。
其中, M_{\mathrm{s}}, C_{\mathrm{s}}, K_{\mathrm{s}} 分别代表 n \times n 的结构质量、阻尼和刚度矩阵, \ddot{X}_{\mathrm{g}}(t) 为地震地面运动加速度时程, I_{\mathrm{s}} 为 n 维的地面运动影响系数列阵, x_{\mathrm{s}}(t) 是结构的动力位移列阵, P_{\mathrm{d}}(t) 为第 d 个位置的阻尼器阻尼力, r_{\mathrm{d}} 为 n 维的阻尼力影响列阵。
阻尼器常用 Maxwell 模型模拟,如图 4 所示,由弹簧和阻尼器两部分组成,其力和变形分别如下式:
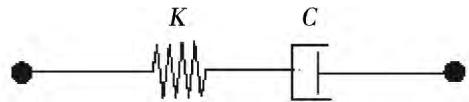
图 4 Maxwell 模型
Fig.4 Maxwell model
力 F = K d_{\mathrm{K}} = C \cdot \operatorname{sgn}(\dot{d}_{\mathrm{C}}) \cdot |\dot{d}_{\mathrm{C}}|^{\alpha} , 变形 d = d_{\mathrm{K}} + d_{\mathrm{C}} , 其中, d_{\mathrm{K}}, d_{\mathrm{C}} 分别为弹簧的变形和阻尼器的变形。对于纯阻尼器, 只要使弹簧刚度 K 足够大, 就可以忽略弹簧的影响。
方程(2)的求解采用非线性时程分析法,求解控制方法使用力控制法,迭代算法使用 Newton Raphson 方法。
5.2 地震动的选择
采用江苏省地震工程研究院提供的苏通大桥桥址处的地震动参数(包括地震加速度反应谱和时程)作为地震输入,2 个概率水平,地震重现期分别为 1000 年和 2500 年。同时以这些反应谱曲线为目标拟合的 10 组地震加速度时程作为地震输入,2500 年重现期的第 1 组水平加速度时程曲线见图 5。
5.3 弹性连接装置参数
在地震反应分析中,弹性连接装置可以用弹性连接单元模拟,参数是弹性刚度值 K 。弹性连接装置对千米级斜拉桥的减震效果就取决于这一刚度值。
为了分析弹性连接装置的弹性刚度 K 对斜拉桥总体地震反应的影响,设定了一系列 K 值进行了地震反应分析: K = 0,2500,5000,7500,10000,12500,
15000,25000,50000,75000,1.0\mathrm{e}5,5.0\mathrm{e}6,1.0\mathrm{e}10~\mathrm{kN / m} 共 14 个值,其中, K = 0 相当于全飘浮体系, K = 1.0\mathrm{e}10 相当于塔梁纵向刚性连接体系。每个 K 值对应的地震反应结果都取 10 组地震动加速度时程所产生的地震反应的平均值。
图 6 到图 9 分别绘出了梁端位移,塔底剪力、弯矩,以及塔顶位移随弹性连接装置的弹性刚度的变化曲线图。从这些图中可以看出,随着弹性连接装置的弹性刚度的增大,梁端位移以及塔顶位移总体显著减小,
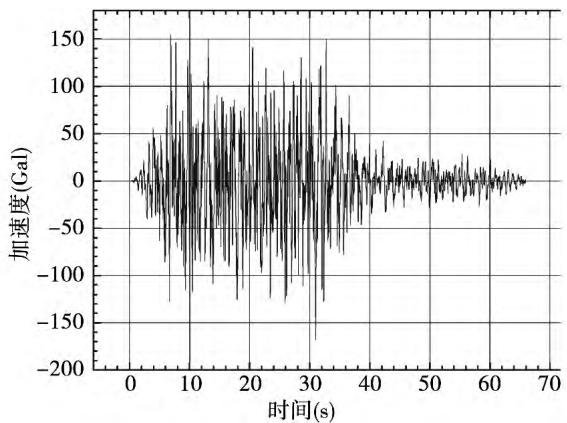
图 5 水平向地震加速度时程
Fig. 5 Longitudinal earthquake acceleration time history
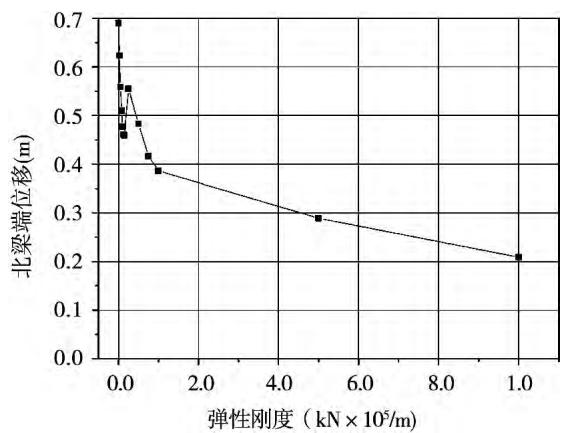
图 6 弹性刚度对北梁端位移的影响
Fig. 6 Influence on the displacement of north beam end caused by elastic stiffness
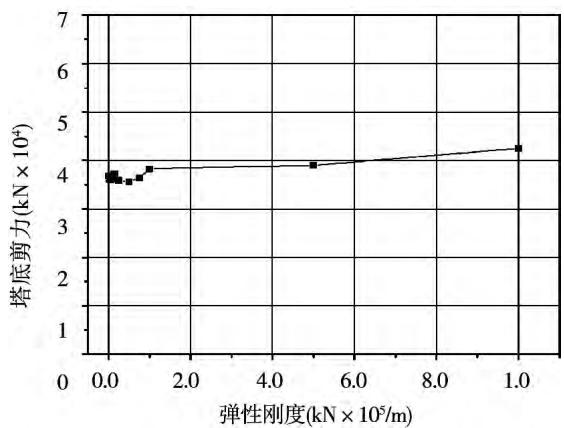
图 7 弹性刚度对北塔塔底剪力的影响
Fig.7 Influence on the shear of north tower bottom caused by elastic stiffness
而塔底剪力和弯矩总体小量增大。可见,通过选取合适的弹性刚度,可以有效地减小塔顶、梁端以及塔梁之间的相对位移,而塔底剪力和弯矩基本不增加。综合考虑梁端位移、塔底剪力和弯矩的变化情况,以及连接装置本身的受力和变形,同时兼顾风荷载、活载和温度等作用下的合理刚度取值,弹性连接装置的刚度取值为 5.0 \times 10^{4} \mathrm{kN / m} 。
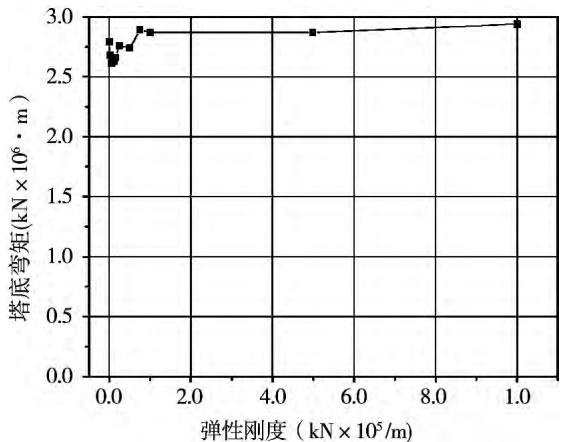
图 8 弹性刚度对北塔塔底弯矩的影响
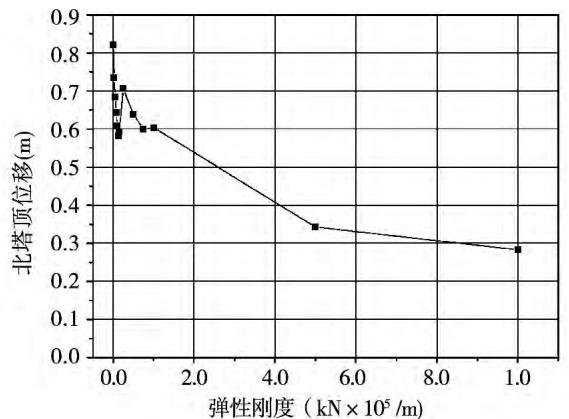
Fig. 8 Influence on the moment of north tower bottom caused by elastic stiffness
Fig.9 Influence on the displacement of north tower top caused by elastic stiffness
图 9 弹性刚度对北塔顶位移的影响
5.4 黏滞阻尼装置参数
从抗震的角度出发,阻尼器的速度指数 \alpha 的常用取值范围为 0.3\sim 1.0 。为了分析阻尼器参数对桥梁减震效果的影响,设定 \alpha 分别为 0.3,0.4,0.5,0.7,1.0 四个值,阻尼系数 C 分别设定为 0,1000,3000,5000,7500,10000,15000,20000,25000 共 9 个值,其中, C = 0 相当于全飘浮体系,总共 50 组参数。每组参数对应的地震反应结果都取 10 组地震动加速度时程所产生的地震反应的平均值。图 10 到图 13 分别绘出了梁端位移,塔底剪力、弯矩,以及塔顶位移随阻尼器参数的变化曲线图。
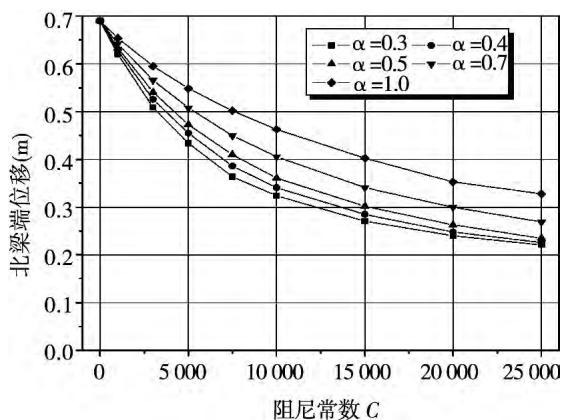
图 10 阻尼器参数对北梁端位移的影响
Fig. 10 Influence on the displacement of north beam end caused by damper parameters
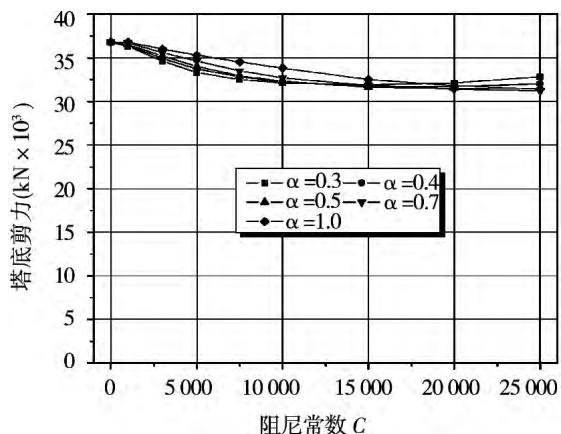
图 11 阻尼器参数对北塔塔底剪力的影响
Fig. 11 Influence on the shear of north tower bottom caused by damper parameters
从这些图中可以看出,当阻尼器的速度指数 \alpha 一定时,随着阻尼系数 C 的增加,阻尼器位移、梁端位移和塔顶位移单调减小,阻尼器的阻尼力单调增加,而塔底剪力和弯矩的变化则有一个低谷,低谷后随着阻尼系数的增大而增大。在很大范围内,塔底剪力和弯矩都明显小于飘浮体系的反应,但如果阻尼系数过大,则会超过飘浮体系。
阻尼器参数的选择由结构的抗震性能决定,以限制主梁的地震位移为目标,同时兼顾主塔的地震内力反应。如果要求将主梁的纵向位移,以及塔梁的相对位移控制在 30~\mathrm{cm} 以内,则可选用阻尼系数 C 为 15000,指数 \alpha 为 0.4 的阻尼器, 地震产生的阻尼器最大变形速度为 0.58 \mathrm{~m} / \mathrm{s} 。
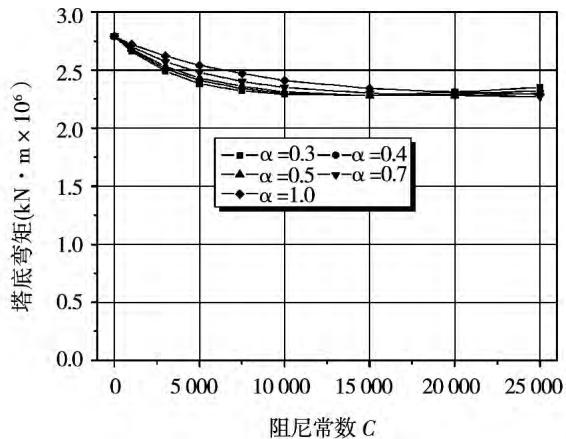
图 12 阻尼器参数对北塔塔底弯矩的影响
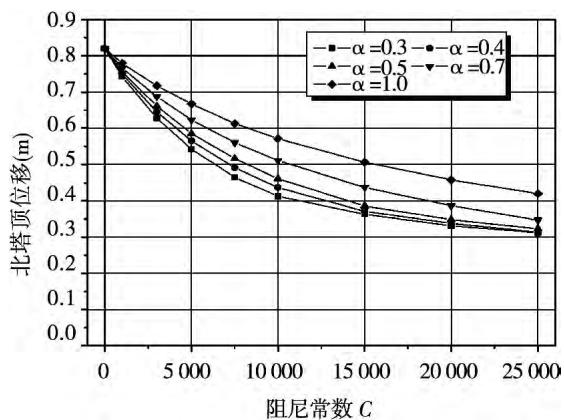
Fig. 12 Influence on the moment of north tower bottom caused by damper parameters
Fig. 13 Influence on the displacement of north tower top caused by damper parameters
图 13 阻尼器参数对北塔顶位移的影响
5.5 弹性连接装置与流体黏滞阻尼器组合装置参数
弹性连接装置与流体黏滞阻尼器组合装置,在塔梁之间设置两个并联的连接单元,一个用线性弹簧模型模拟,另一个用 Maxwell 模型模拟。模型参数中,弹簧刚度 K 取为前述弹性连接装置参数,阻尼系数 C 取为前述流体黏滞阻尼器装置参数即可。
6 计算结果与讨论
在合理选择参数的前提下,对 3 种减震体系:弹性连接装置 K = 5.0 \times 10^{4} \mathrm{kN / m} ,液体黏滞阻尼器装置 \alpha = 0.4, C = 15000 ,以及两者的组合装置,分别进行了分析,得到相应的结果,表 2 对它们的减震效果进行了比较。
Table 2 Earthquake-reduction effect comparison of three kinds connecting device
表 2 三类连接装置的减震效果比较
| 位置 | 分量 | 弹性连接装置 | 液体黏滞阻尼器 | 组合装置 |
|---|---|---|---|---|
| 北塔连接装置 | 力(kN) | 2.10e4 | 1.210e4 | 1.08e4 |
| 变形(m) | 0.421 | 0.293 | 0.231 | |
| 北塔底截面 | 剪力(kN) | 3.56e4 | 3.17e4 | 3.01e4 |
| 弯矩(kN.m) | 2.74e6 | 2.28e6 | 2.05e4 | |
| 北梁端 | 位移(m) | 0.483 | 0.285 | 0.215 |
| 北塔顶 | 位移(m) | 0.637 | 0.371 | 0.318 |
| 南塔连接装置 | 力(kN) | 2.20e4 | 1.160e4 | 0.92e4 |
| 变形(m) | 0.439 | 0.271 | 0.223 | |
| 南塔底截面 | 剪力(kN) | 3.96e4 | 3.43e4 | 3.12e4 |
| 弯矩(kN.m) | 2.50e6 | 1.74e6 | 1.46e4 | |
| 南梁端 | 位移(m) | 0.47 | 0.272 | 0.211 |
| 南塔顶 | 位移(m) | 0.625 | 0.368 | 0.302 |
从表 2 中可见:与设置弹性连接装置相比,设置液体黏滞阻尼器后,梁端位移减小了 42\% ,塔底剪力、弯矩分别减小了 12\% ,23\% ;设置组合装置后,梁端位移减小了 56\% ,塔底剪力、弯矩分别减小了 16\% ,25\% 。另外,连接装置的力(阻尼力)和位移也有同样的变化趋势。
设置阻尼器后,梁端位移较小,同时减小了主塔的内力。组合装置的效果更好,但是要付出更多的经济代价。
7 结语
由上述分析可知:
(1) 飘浮体系的千米级斜拉桥可以采用两种途径减小梁端位移:一是适当增大结构的刚度;二是增大桥梁结构的阻尼,在塔梁间增设阻尼装置。
(2) 弹性连接装置对千米级斜拉桥的减震效果取决于弹性刚度值 K 。液体黏滞阻尼器对千米级斜拉桥的减震效果取决于阻尼器的参数 C 和 \alpha 。
(3) 只要选择合理的参数, 设置液体黏滞阻尼器可以显著地改善整个斜拉桥的地震反应。对于本文的桥梁模型, 如果要将主梁的纵向位移控制在 30 \mathrm{~cm} 以内, 可以选用阻尼系数 C 为 15000 , 指数 \alpha 为 0.4 的阻尼器。
(4) 三类塔梁连接装置(弹性连接装置、阻尼器和组合装置)均能有效地减小梁端的地震位移,但组合装置的减震效果最好,单纯阻尼器减震效果也较理想。
修建超大跨度斜拉桥时的纵向减震体系设计,可以参考和借鉴本文的研究分析方法。
参考文献:
Fleming J F, Egeseli E A. Dynamic behavior of a cable-stayed bridge. Earthquake Engineering and Structural Dynamics, 1980(8): 1-16. ↩
Abdel-Ghaffar A M. Cable-stayed bridges under seismic action [C] // Proceedings of the Seminar Cable-Stayed Bridges: Recent Developments and Their Future, Amsterdam: Elsevier Science Publisher, 1991: 171-191. ↩
严国敏,现代斜拉桥 [M]. 成都:西南交通大学出版社,1997:140-142. YAN Guomin. Modern cable stayed bridge [M]. Chengdu: Southwest Jiaotong University Press, 1997, 140-142. (in Chinese) ↩
范立础,胡世德,叶爱君. 大跨度桥梁抗震设计 [M]. 北京:人民交通出版社,2001,43-59. FAN Lichu, HU Shide, YE Aijun. Seismic design for long span bridge [M]. Beijing: People's Communications Publishing House, 2001, 43-59. (in Chinese) ↩
范立础. 桥梁抗震 [M]. 上海: 同济大学出版社, 1997: 117-154. FAN Lichu. Seismic design for highway bridge [M]. Shanghai: Tongji University Press, 1997, 117-154. (in Chinese)
李立峰,刘本永,张晨熙,等.中等跨径斜拉桥塔梁弹性约束装置的减震效应研究 [I]. 地震工程与工程振动,2013, 33(1): 146-152. LI Lifeng, LIU Benyong, ZHANG Chenxi, et al. Research on the seismic performance of mid-span cable-stayed bridges with elastic constraints between tower and beam [II]. Earthquake Engineering and Engineering Dynamics, 2013, 33(1): 146-152. (in Chinese)
范立础,王志强. 桥梁减隔震设计 [M]. 北京:人民交通出版社,2001. FAN Lichu, WANG Zhiqiang. Seismic isolation design for highway bridge [M]. Beijing: People's Communications Publishing House, 2001. (in Chinese) ↩
Priestly M J N, Seible F, Calvi G M. Seismic design and retrofit of bridges [M]. John Wiley & Sons, New York, 1996, 457-533. ↩
Mahendra P Singh, F. ASCE, Navin P Verma, et al. Moreschi, Seismic analysis and design with Maxwell dampers []. Journal of Engineering Mechanics, 2003, 129(3): 273-282.
ADINA. User's Guide [M]. Adina R&D, Inc., Watertown, MA, 1995.
Nazmy Aly S, Abdel-Ghaffar A M. Non-linear earthquake-response analysis of long-span cable-stayed bridges: theory [I]. Earthquake Engineering and Structural Dynamics, 1990(19): 45-62.
Chopra A K. Dynamics of structures [M]. Prentice-Hall, Englewood Cliffs, NJ, 2000. ↩
Clough R W, Penzien J. Dynamics of structures [M]. 2nd ed., McGraw-Hill, NewYork, 1995: 191-196. ↩
杨喜文,张文华.李建中.大跨度斜拉桥横桥向减震研究Ⅱ.地震工程与工程振动,2012,32(1):86-92. YANG Xiwen, ZHANG Wenhua, LI Jianzhong. Seismic design for long-span cable-stayed bridges in transverse direction. Earthquake Engineering and Engineering Dynamics, 2012, 32(1): 86-92. (in Chinese) ↩
董胜利,元兴军. 大跨斜拉桥减震控制分析 [I]. 铁道工程学报,2007,7(106):47-51. DONG Shengli, QI Xingjun. Seismic response control analysis of long-span cable-stayed bridge [J]. Journal of Railway Engineering Society, 2007, 7(106): 47-51. (in Chinese) ↩
张永亮,陈兴冲.客运专线大跨斜拉桥减震方案优化分析Ⅱ.应用基础与工程科学学报,2014,1(22):160-169. ZHANG Yongliang, CHEN Xingchong. Optimization analysis of the seismic damping scheme for long-span cable-stayed bridges on a passenger-dedicated railway line [J]. Journal of Basic Science and Engineering, 2014, 1(22): 160-169. (in Chinese) ↩