韩振峰1, 叶爱君2
(1. 合肥学院建筑工程系,安徽合肥 230601;2. 同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:首先考虑场地和视波速等因素,从已知脉冲型地震合成相关点的脉冲型非一致地震动;其次建立了千米级斜拉桥有限元模型,进行了非一致地震反应分析,考虑了几何非线性,结果表明混合场地以及较低的视波速为该类型桥梁的最不利工况;然后对弹性连接和黏滞阻尼器 2 种减震方式进行了参数分析;最后对 2 种方式的减震效果进行了比较,结果表明:黏滞阻尼器在脉冲非一致地震动下的减震效果不如在一致地震动输入情况下的明显,对塔底弯矩的减震效果甚至不如弹性连接方式。修建更大跨径的斜拉桥,其脉冲非一致地震动下的减震设计,可能需要另寻它法。
关键词:斜拉桥;脉冲型地震;非一致激励;减震;视波速
中图分类号:U448.27 文献标志码:A
Research on the seismic reduction of cable-stayed bridges over kilometers under pulse-type non-uniform earthquake action
HAN Zhenfeng ^{1} , YE Aijun ^{2}
(1. Department of Architectural Engineering of Hefei University, Hefei 230601, China; 2. State Key Laboratory
for Disaster Reduction of Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: Firstly, the pulse type non-uniform ground motions at related position were synthesized from the recorded pulse ground motions with the factors of ground condition and apparent wave velocity were considered. Secondly, the finite element model of a cable-stayed bridge over kilometers was built; the geometric nonlinearity was taken into account; the non-uniform seismic response analysis was conducted, and the results show that the mixed ground condition and lower apparent wave velocity is the most unfavorable conditions for this kind bridge. Thirdly, parameters analyses were conducted on the elastic connections and viscous dampers devices. Lastly, seismic reduction efficacy of the two devices were compared, and the results show that the viscous dampers under the non-uniform ground motion is poor than that under the uniform ground motion, and its reduction efficacy of bending moment at the tower bottom is even poor than that of elastic connection device. When building longer span cable-stayed bridge, the seismic reduction design under pulse type non-uniform ground motion may need to find another method.
Key words: cable-stayed bridge; pulse type earthquake; non-uniform excitation; seismic reduction; apparent wave velocity
引言
大型越江或跨海桥梁工程可能会采用跨度超越千米的斜拉桥结构,超越千米的跨径带来了地震动的非一致性问题。尤其当这些桥梁位于近断层地带时,还会受到脉冲型地震动的影响。脉冲型非一致地震作用下千米级斜拉桥的抗震安全性是必须要解决的一个重要课题1。
文献2,3对跨径在 $500\mathrm{m}$ 内的斜拉桥减震控制进行了研究,针对相应的结构采取了一些减震装置,进行了减震分析。文献4对 $1000\mathrm{m}$ 级斜拉桥的减震机理和方法进行了系统研究,并且给出了该类桥梁纵向合理减震体系,但是上述研究是以远场一致地震动为研究对象的。文献5对主跨为 $392\mathrm{m}$ 的斜拉桥进行非一致地震激励反应分析,得出非一致激励使塔顶和梁端位移增加,以及使得塔底和墩底的内力增大。另外,文献还进行了黏滞阻尼器的减震设计,得出黏滞阻尼器能减小结构内力和位移。文献6对主跨为 $490\mathrm{m}$ 的斜拉桥进行了减震分析,得出考虑行波效应后,半主动控制优于被动控制的结论。这些研究是以远场非一致地震动为研究对象的。针对近断层脉冲非一致地震动作用下的 $\mathrm{km}$ 级斜拉桥的减震研究,还比较少。
要解决这个问题,首先要搞清楚超 $\mathrm{km}$ 级斜拉桥在脉冲非一致激励地震动下地震反应特性。文献7考虑了地震动的空间差异性,对一主跨为 $420\mathrm{m}$ 的斜拉桥进行了非一致激励研究,得出了行波效应对地震响应影响很大等结果。文献8对主跨为 $680\mathrm{m}$ 的斜拉桥进行了研究,得出大跨斜拉桥需要考虑非一致地震激励以及场地条件和行波效应。文献9对主跨为 $260\mathrm{m}$ 的永和桥进行了行波效应分析,得出相位差效应对漂浮体系的斜拉桥是有利的。文献10对主跨为 $1088\mathrm{m}$ 的苏通大桥进行行非一致地震反应分析,得出非一致地震响应多数情况下比一致地震响应要大,但是该文献的重点是研究地震动的生成方法。文献11对主跨为 $708\mathrm{m}$ 的双层斜拉桥进行了行波效应分析,考虑了非线性因素,得出行波效应对斜拉桥的影响取决于视波速。遗憾的是上述这些研究都没有以近断层脉冲型地震动为研究对象。
现有的研究都不能解决这个问题,因此需要进行新的研究。为此目的,首先对非一致地震动的特点进行了描述,在考虑场地和视波速等因素的基础上,采用从已知脉冲型地震动合成相关点脉冲型非一致地震动的方法,生成了脉冲型非一致地震动;其次建立了相应的 $1000\mathrm{m}$ 级斜拉桥有限元模型,考虑了几何非线性;然后进行了非一致地震反应分析,结果表明混合场地以及较低视波速条件下的脉冲非一致输入,为该类型桥梁的最不利工况;随后对弹性连接和黏滞阻尼器两种减震方式进行了参数分析;最后在上述最不利工况条件下,对 2 种方式的减震效果进行了比较,结果表明在脉冲非一致地震动下,黏滞阻尼器的减震效果不如在一致地震动输入情况下的明显,对塔底弯矩的减震效果甚至不如弹性连接方式。
1 脉冲型非一致地震动的生成
1.1 脉冲型非一致地震动
大跨径斜拉桥的各支承点的地震动是不同的,其幅值、相位和频谱特性都在变化,各点地震动之间存在相关性。地震动的空间相关性可以采用相干函数来描述。Kiureghian 从理论上对地震动相干函数进行了研究12,得出相干函数的影响因素主要包括:不相干效应、行波效应、衰减效应和局部场地效应。其中,衰减效应影响最小。研究人员根据 SMART1、LSST 的地震动观测记录,提出了多种相干函数经验模型,并且通过回归分析确定了模型中的回归参数。经验模型主要有 Harichandran 模型、Hao 和 Oliverra 模型、Abrahamson 模型和 Yang 模型等13,14,15,16。
近断层地震动与远离断层区的地震动存在着明显区别,其中速度脉冲效应带来的地面和结构的破坏已经被观测证实。脉冲型地震动作用下考虑地震动的非一致效应,桥梁结构的地震反应如何变化,目前尚不明确。
1.2 脉冲型非一致地震动的生成
脉冲型非一致地震动的来源分两类:实际地震动记录和人工产生的地震动。由于地震记录的局限性(场地、震级、震源、千米尺度的台阵等),符合要求的实际地震动记录几乎没有。因此,人工合成脉冲型非一致地震动是现在唯一的选择。人工合成地震动目前主要有 2 种方法:基于随机振动方法、和基于断层模拟和波动理论的有限元方法。前者比较方便,后者比较复杂和耗机时,实际使用中采用前者居多。
基于随机振动方法,在合成一致地震动方面主要是根据功率谱 (或目标反应谱) 和相干函数,使用傅立叶逆变换,合成平稳地震动,并且通过包络函数或相位差谱来体现地震动的非平稳性。
脉冲型一致地震动的合成方法,主要是根据简化脉冲模型合成低频脉冲成分,同时采用基于功率谱 ( 或
目标反应谱、或相位差谱和相位导数 ) 的方法合成一致地震动的高频部分,然后将两者叠加得到脉冲型一致地震动。
脉冲型非一致地震动的合成现在做的较少,本文采用从已知脉冲型地震动合成相关点脉冲型非一致地震动的方法。具体做法:(1) 选择一个典型的脉冲地震动时程,计算该时程的包络函数、功率谱(或相位差谱);(2) 将该时程的包络函数,作为其他支承点时程的包络函数;(3) 选择相干函数;(4) 根据场地条件、相干函数和已知时程的功率谱(或相位差谱),确定场地中各支承点的功率谱(或相位差谱);(5) 根据各点的功率谱(或相位差谱)和包络函数,使用傅里叶逆变换,生成各点地震动,它们具有脉冲性和非一致性。
近场脉冲型地震波的选择原则如下:(1) 震源距断层最近距离小于 $10\mathrm{km}$ ;(2) 脉冲周期超过 $10\mathrm{s}$ 。根据上述原则,在 PEER(Pacific Earthquake Engineering Research Center) 的 NGA(Next Generation Attenuation) 地震动数据库中选择了 5 组地震动,均为台湾集集地震数据,表 1 为该 5 组地震动的基本参数。空间各点的相干函数采用 Harichandran-Vanmarcke 模型13,该模型是基于台湾 SMART1 台网提出的。
为了模拟场地条件的变化,在不同支承点考虑不同的场地类型组合,设计了 3 种组合:岩石场地 + 岩石场地,软土场地 + 软土场地,岩石场地 + 软土场地。考虑行波效应,视波速的取值为 $2, 2.5, 3, 3.5 \mathrm{~km} / \mathrm{s}$ 。在单个支承点处总计生成 12 条地震动时程,模拟场地组合的 3 种变化和视波速的 4 种变化。
为了便于研究和对比,将各条地震动的 PGA 峰值统一调整为 $0.8\mathrm{g}$ ,使得动力非线性效应更显著。
Table 1 Basic parameters of near field pulse type ground motion
表 1 近场脉冲型地震动基本参数
| 组号 | 观测站点 | 震级 | 震中距(km) | 与震源最近距离(km) | 脉冲周期(s) | PGA(g) | PGV(cm/s) |
|---|---|---|---|---|---|---|---|
| 1 | TCU049 | 7.62 | 39.73 | 3.78 | 11.655 | 0.29 | 46.1 |
| 2 | TCU053 | 7.62 | 41.97 | 5.97 | 12.845 | 0.22 | 40.9 |
| 3 | TCU054 | 7.62 | 38.48 | 5.30 | 10.472 | 0.16 | 60.4 |
| 4 | TCU068 | 7.62 | 48.52 | 0.32 | 12.166 | 0.57 | 184.6 |
| 5 | TCU122 | 7.62 | 23.22 | 9.35 | 10.878 | 0.22 | 42.4 |
2 有限元模型
2.1 模型描述
某全长为 $2088\mathrm{m}$ 的七跨主梁连续双塔斜拉桥,中跨为 $1088\mathrm{m}$ ,边跨为 $300\mathrm{m} + 2\times 100\mathrm{m}$ ,采用倒 Y 形混凝土塔,桥面为钢箱梁,下横梁与主梁之间无支座装置,塔基采用高桩承台群桩基础,边墩顶纵向均设置滑动支座。
有限元分析模型17中,主梁、塔和边墩用梁单元模拟,计入恒载几何刚度(由恒载轴力引起的);主梁和斜拉索之间采用主从连接;斜拉索采用桁架单元,该单元计入拉索的垂度效应和恒载几何刚度;主梁与塔和边墩纵向均无约束,横向均为主从约束;墩底(承台顶)为固结边界条件;模型如图 1 所示。
模型采用瑞利阻尼假设;采用线性弹簧单元模拟弹性连接装置;采用非线性弹簧单元模拟黏滞阻尼器 (Maxwell 模型),其中弹簧刚度取 $1.0\mathrm{E}10\mathrm{kN / m}$ ,阻尼参数根据分析来设置。

图 1 有限元模型
Fig.1 Finite element model
2.2 分析方法
待求解问题可以描述为: 一个具有 $n$ 个自由度的斜拉桥结构, 附加的流体黏滞阻尼器设置在 $m$ 个不同的位置上, 受到脉冲型非一致地震动作用, 求该结构的地震反应, 采用大质量法, 同时需要考虑动力几何非线性。
基础支承点附加大质量单元取为结构总质量的 $10^{6}$ 倍,释放基础运动方向的约束,并且在大质量点施加动力时程。由于大跨斜拉桥基频较小,大质量法的数值计算精度是可以得到保证20。
动力分析时的初始状态采用的是斜拉桥的成桥状态,将恒载产生的轴向力转化为几何刚度,分别对应于索、主塔、墩、梁的几何刚度,同时考虑大变形和大变位18,19。
2.3 支承点地震动
根据 1.2 节的方法,结合斜拉桥模型,沿桥梁纵向选择北边墩底 (位置 A)、北塔底(位置 B)、南塔底(位置 C) 和南边墩底(位置 D)4 个位置作为关键支承点,如图 2 所示。生成的非一致地震动时程工况组合,如表 2 所示。辅助墩底支承点地震动与相应边墩底支承点的相同。
以表 1 中第 1 组脉冲地震动为已知脉冲型地震动,生成表 2 中的人工地震动时程,图 3~图 6 为表 2 工况 1 地震动时程图 (其余的工况类似)。从人工地震动的频谱分析对比和速度时程曲线,可以得出人工地震波具有脉冲性,频谱成分类似。

图 2 关键支承点
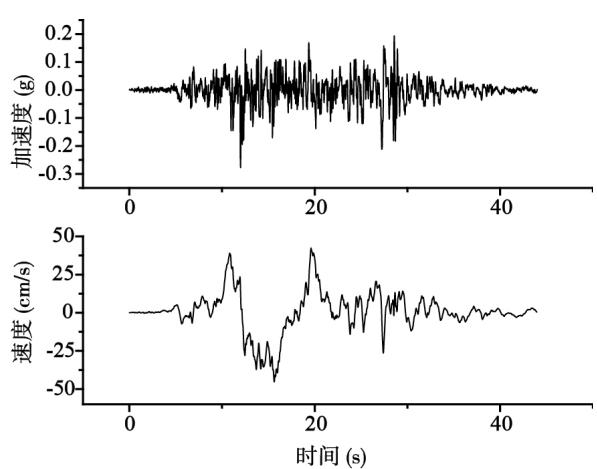
图 3 第 1 组选择的脉冲地震动(垂直断层水平方向)
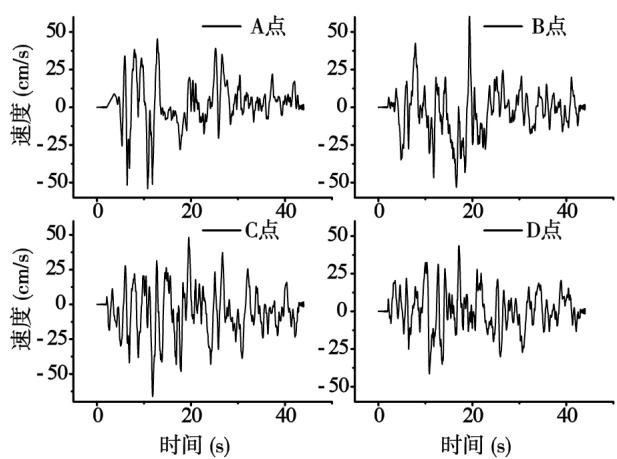
Fig.3 Selected pulse ground motion group 1 (vertical fault horizontal direction)
图 5 工况 1 人工脉冲波的速度时程
Fig. 5 Artificial pulse velocity time history of load condition 1
Table 2 Load condition of the non-uniform ground motion
表 2 非一致地震动工况
| 工况 | 组合 | 支承点A,B | 支承点C,D | 视波速(km/s) |
|---|---|---|---|---|
| 1~4 | 组合一 | 岩石场地 | 岩石场地 | 依次取2,2.5,3,3.5 |
| 5~8 | 组合二 | 岩石场地 | 软土场地 | 依次取2,2.5,3,3.5 |
| 9~12 | 组合三 | 软土场地 | 软土场地 | 依次取2,2.5,3,3.5 |
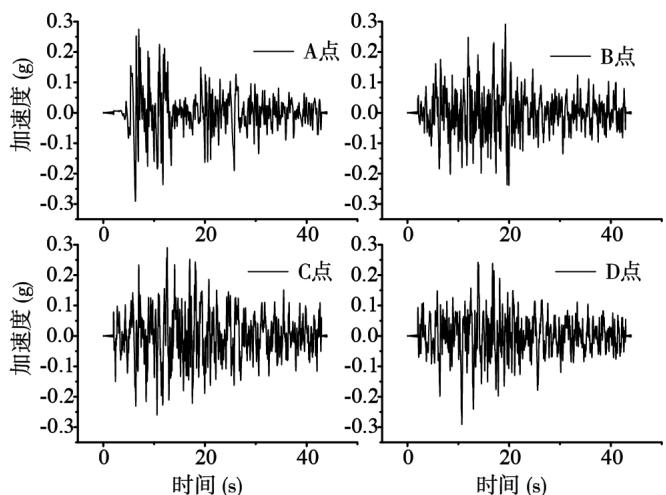
Fig.2 The key support point (Unit:m)
图 4 工况 1 人工脉冲波的加速度时程
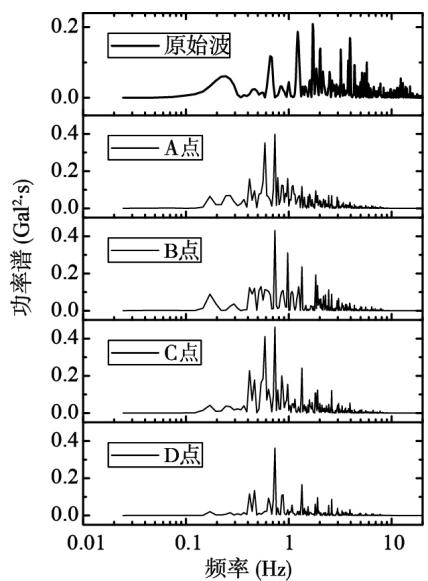
Fig.4 Artificial pulse acceleration time history of load condition 1
Fig.6 Spectrum analysis of artificial pulse of load condition 1
图 6 工况 1 人工脉冲波的频谱分析
3 非一致地震反应分析
从表 2 中知,组合一全部支撑均为岩石场地;组合二支撑 A、B 为岩石场地,支撑 C、D 为软土场地;组合三全部支撑均为软土场地。组合一对应工况 14,组合二对应工况 58,组合三对应工况 912;视波速依次取 2、2.5、3、3.5km/s。对桥梁模型进行非线性动力分析,采用上述 3 种组合,计算结果取 5 组地震动的平均值。图 7图 9 分别为 3 个组合的分析结果图示,其中梁端指主梁两端节点,塔顶指主塔顶部节点,塔底指倒 Y 形塔的塔柱底部节点。
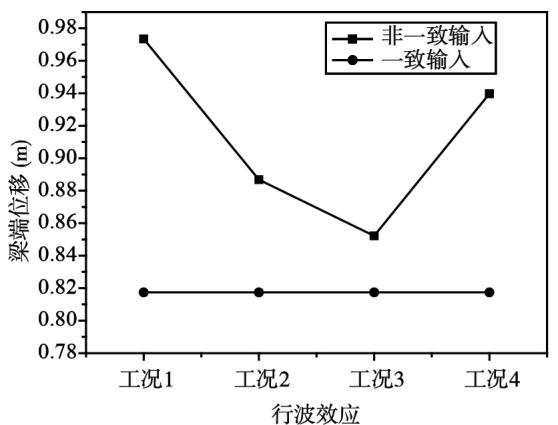
(a)梁端位移
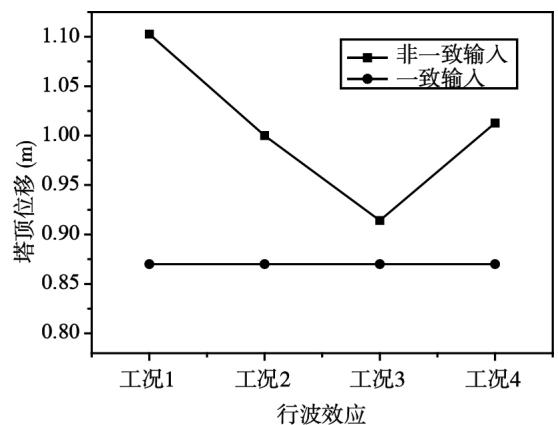
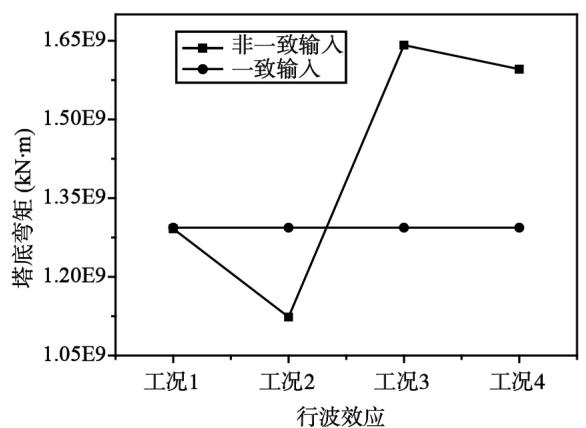
(c)塔底弯矩
图 7 组合一分析结果
Fig.7 Analysis results of combination 1
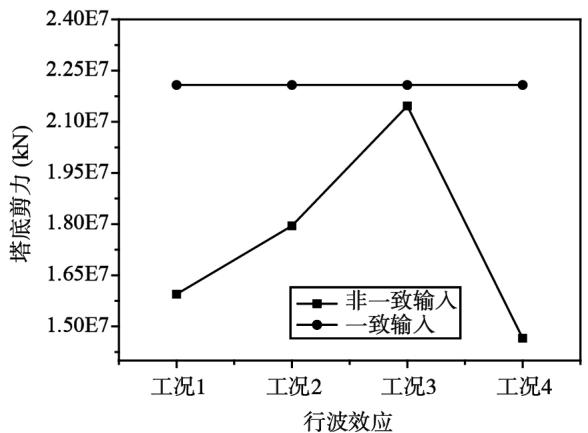
(d)塔底剪力
从图 7 中可以看出,梁端位移和塔顶位移,不同视波速下非一致输入的计算结果均比一致输入的计算结果要大,但是位移值随视波速的增大,先趋于减小然后增大,在视波速为 $3\mathrm{km / s}$ 时达到最低值。塔底弯矩,随视波速的增大,先减小后增大, $2\mathrm{km / s}$ 和 $2.5\mathrm{km / s}$ 时,非一致输入结果比一致输入的小; $3\mathrm{km / s}$ 和 $3.5\mathrm{km / s}$ 时,非一致输入结果比一致输入的大。塔底剪力,随视波速的增大,先增大后减小,非一致输入结果均比一致输入的小。
从图 8 中可以看出,梁端位移和塔顶位移,不同视波速下非一致输入的计算结果均比一致输入的计算结果要大,但是位移随视波速的增大,先增大后减小,有一个峰值,在视波速为 $2.5\mathrm{km / s}$ 时达到。塔底弯矩和剪力均随视波速的增大,先增大后减小,再增大,弯矩值非一致输入结果比一致输入结果大,剪力值在视波速为 $2.5\mathrm{km / s}$ 时比一致输入结果小,其余视波速值时比一致输入结果大。
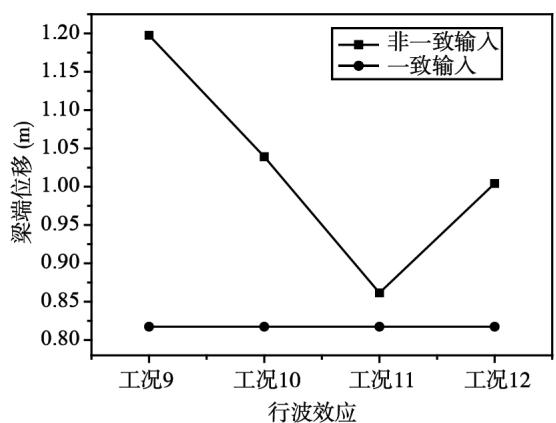
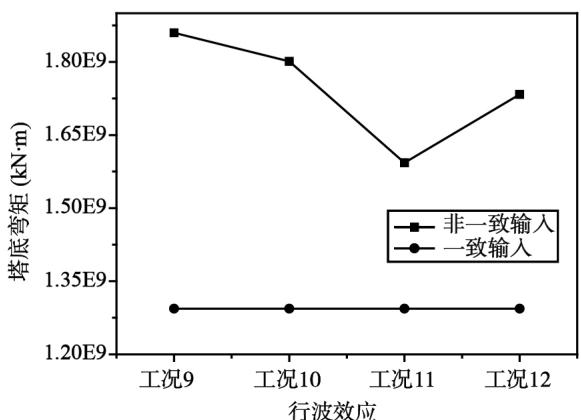
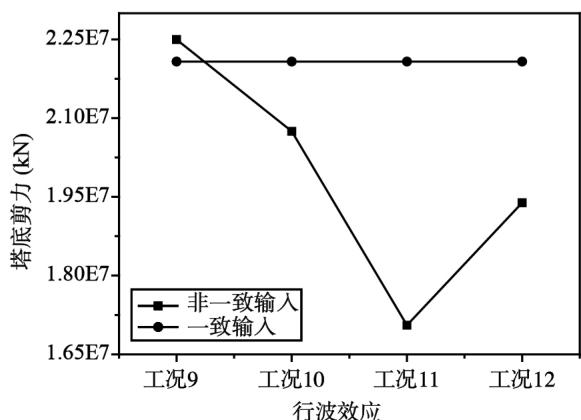
从图 9 中可以看出,梁端位移和塔顶位移,不同视波速下非一致输入的计算结果均比一致输入的计算结果要大,但是位移随视波速的增大,先减小后增大,在视波速为 $3\mathrm{km / s}$ 时达到最低值。塔底弯矩和剪力,均随视波速的增大,也先减小后增大,最低值也在视波速为 $3\mathrm{km / s}$ 时达到,弯矩值非一致输入结果比一致输入的大,剪力值非一致输入结果比一致输入的小。
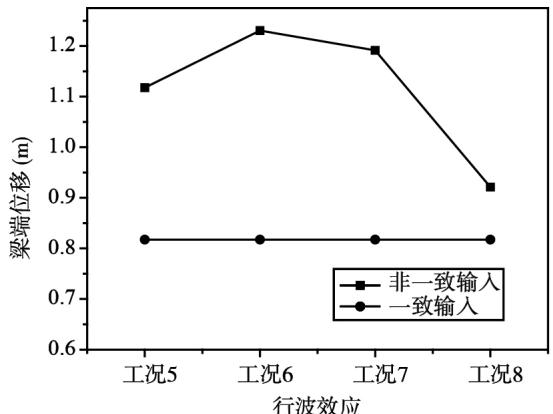
(a)梁端位移
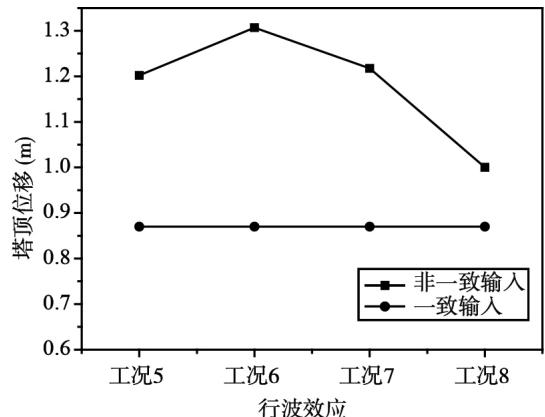
(b)塔顶位移
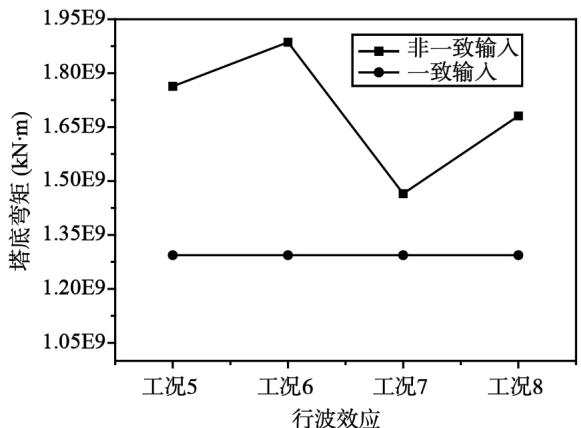
(c)塔底弯矩
图 8 组合二分析结果
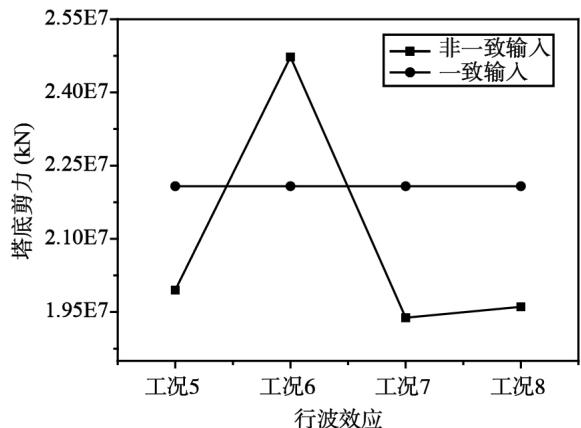
(d)塔底剪力
(a)梁端位移
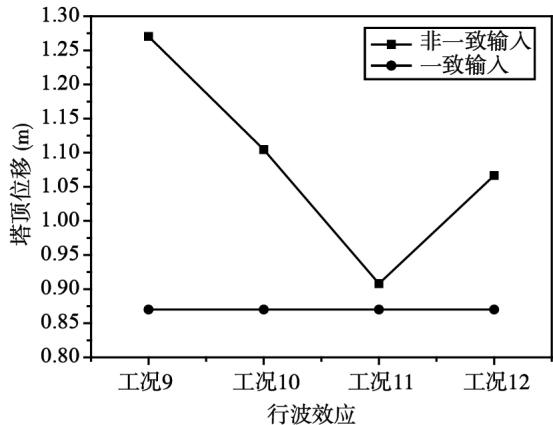
Fig.8 Analysis results of combination 2
(b)塔顶位移
(c)塔底弯矩
图 9 组合三分析结果
Fig.9 Analysis results of combination 3
(d)塔底剪力
综上所述,位移和弯矩值,各组合的非一致输入结果比一致输入结果大;剪力值,各组合的非一致输入结果基本上比一致输入结果小。这种现象的原因可能是非一致输入的相干性加强了关键构件的位移和弯矩反应,对剪力反应来说与弯矩变化相反。视波速的增大不一定会增加反应值而最大位移和内力在某一视波速下达到,具体波速值与结构和脉冲地震动有关,不能定性确定。
表 3 列出了各个组合最大反应值及其对应的视波速。已知组合一为单一岩石场地,组合二为混合场地,组合三为单一软土场地。从该表中可以看出,混合场地下的非一致地震反应值最大,单一软土场地其次,单一岩石场地最小。软土场地的低频成分能放大结构反应,与现有的研究结果是类似的;但是混合场地的非一致地震反应值要高于单一软土场地,主要是由于混合场地的土层差异产生的拟静力效应较大,补偿了单一岩石场地与单一软土场地之间产生的差异。
另外,最大反应值对应的视波速在 $2.5\mathrm{km / s}$ 附近,说明低视波速为不利的情况,高视波速反而对结构反应有利,其行波效应较小。
得出结论,混合场地以及较低的视波速条件下的脉冲非一致输入,为该类型桥梁的最不利工况。
Table 3 The maximum non-uniform response and apparent wave velocity
表 3 最大非一致反应值及视波速
| 组 合 | 比较值 | 梁端位移(m) | 塔顶位移(m) | 塔底弯矩(kN·m) | 塔底剪力(kN) |
|---|---|---|---|---|---|
| 一 | 反应值 | 0.97 | 1.10 | 1.64E+09 | 2.15E+07 |
| 视波速(km/s) | 2 | 2 | 3 | 3 | |
| 二 | 反应值 | 1.23 | 1.31 | 1.89E+09 | 2.47E+07 |
| 视波速(km/s) | 2.5 | 2.5 | 2.5 | 2.5 | |
| 三 | 反应值 | 1.20 | 1.27 | 1.86E+09 | 2.25E+07 |
| 视波速(km/s) | 2 | 2 | 2 | 2 |
4 减震参数分析
漂浮型斜拉桥的纵桥向减震的目的是减小位移,不增加内力。文献21指出,纵向漂浮型千米级斜拉桥,可采用弹性索、阻尼器和限位阻尼器等装置进行减震。结合千米级斜拉桥的特点和现有的工程经验,采用 2 种减震方法,在塔梁之间分别采用:(1)弹性连接 (方法一);(2) 黏滞阻尼器(方法二)。
从前面分析知,混合场地以及较低的视波速为最不利工况。因此下面的研究,在该最不利工况下进行。
4.1 方法一
方法一采用弹性连接,用线性弹簧单元模拟。设定弹簧刚度值分别取:0、5e3、1.0e4、1.5e4、2.5e4、5.0e4、7.5e4、1.0e5、1.0e6 kN/m 共 9 个值。每个刚度值的地震反应结果均取 5 组地震动的反应平均值。
非一致输入工况选择混合场地及视波速为 $2.5\mathrm{km / s}$ 。对比工况为该混合场地的一致输入,不考虑视波速等效应。
图 10~ 图 12 分别为 2 个工况的典型反应值随弹簧刚度的变化曲线图。从图中可以看出,对于梁端位移,2 个工况均先增加然后减小;对于塔底弯矩和剪力,2 个工况的变化规律基本相似,均在弹簧刚度较小时达到峰值,然后随着该刚度的增大,达到最低值,过后又增大。其原因是弹簧刚度较小时,对斜拉桥动力特性的影响很小,结构反应会持续增大;弹簧刚度增大到一定值以后,开始影响低阶振型,结构反应开始减小;弹簧刚度再继续增大时间,低阶振型完全被抑制住了,但是激起了斜拉桥的高阶振型,又导致了动力反应增大。
由上可知,弹性连接装置对 2 个工况的减震影响基本相同。在非一致输入情况下,增大弹簧刚度,可以
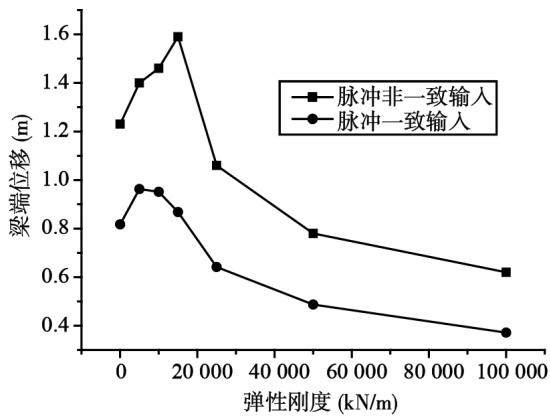
图 10 梁端位移随弹簧刚度的变化
Fig. 10 Variation of the beam end displacement with spring stiffness
减小梁端位移,但是塔底弯矩和剪力变化比较起伏。考虑在内力反应最低值处,兼顾梁端位移反应值,建议选择弹簧刚度值为 $5.0\mathrm{e}4\mathrm{kN / m}$ 。
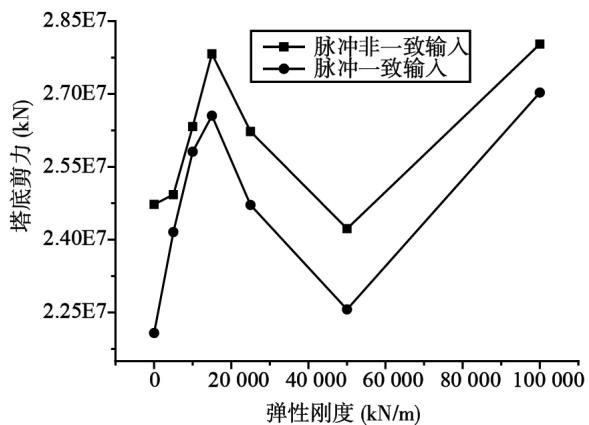
图 11 塔底剪力随弹簧刚度的变化
Fig. 11 Variation of the shear of tower bottom with spring stiffness
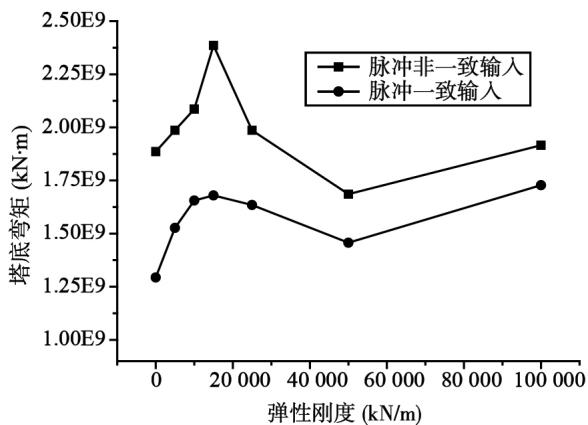
图 12 塔底弯矩随弹簧刚度的变化
Fig. 12 Variation of the moment of tower bottom with spring stiffness
4.2 方法二
方法二采用黏滞阻尼器,速度指数 $\alpha$ 设定为 0.3、0.5、0.7、1.0 共 4 个值,阻尼系数 $C$ 设定为 0、5.0e3、1.0e4、1.5e4、2.0e4、2.5e4 共 6 个值,总共 24 组参数。每组参数对应的地震反应结果均取 5 组地震动的反应平均值。
非一致输入工况和对比工况与方法一相同。图 13~图 15 分别为 2 个工况的的典型反应值随阻尼参数的变化曲线图。
从图中可以看出,对于梁端位移,2 个工况的规律基本类似,随参数 $C$ 的增加,位移反应均减小;对于塔底弯矩和剪力,随参数 $C$ 的增加,2 个工况均先减小,然后略微增大,再接近平稳,但是 2 个工况反应值的最低点位置不同。非一致输入情况下,反应最低值在参数 $C$ 较大时达到。另外,2 个工况随指数 $\alpha$ 的增大,均会减小反应值。其原因是黏滞阻尼器随参数的增加,对斜拉桥动力特性的影响是及时的,结构反应随后开始减小,同时黏滞阻尼器参数的持续增加对斜拉桥高阶振型的影响较小。
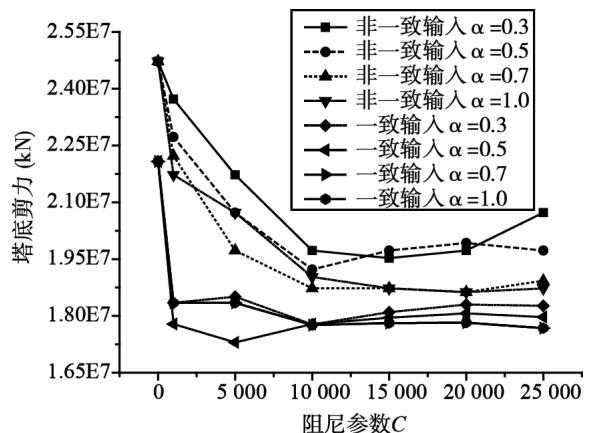
图 14 塔底剪力随阻尼参数的变化
Fig. 14 Variation of the shear of tower bottom with damper parameters
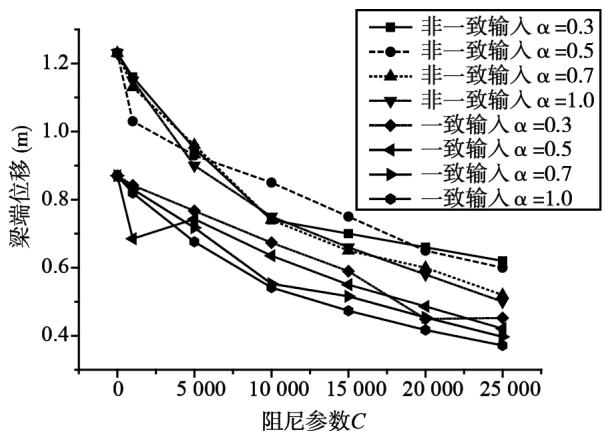
图 13 梁端位移随阻尼参数的变化
Fig. 13 Variation of the beam end displacement with damper parameters
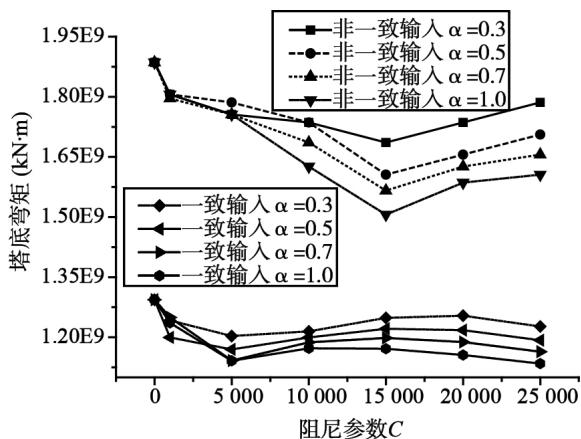
图 15 塔底弯矩随阻尼参数的变化
Fig. 15 Variation of the moment of tower bottom with damper parameters
由上可知,阻尼器参数对 2 个工况的减震影响有轻微差别,总体上趋势相同。在非一致输入情况下,考虑控制内力反应,同时约束位移,建议选择阻尼系数 $C$ 为 1.5e4,指数 $\alpha$ 为 0.7。
5 减震比较
在最不利工况下,分别采用上述 2 种减震方法,减震参数取上述建议值,进行非一致动力分析,比较关键部位的地震反应,结果如表 4 所示。从中可以看出,与漂浮体系反应相比,减震方法 1 的塔底弯矩和剪力,分别减小了 32% 和 20% ;梁端和塔顶位移,分别减小了 36.6% 和 37.2% 。减震方法 2 的塔底弯矩和剪力,分别减小了 21% 和 28% ;梁端和塔顶位移,分别减小了 47.2.6% 和 46.5% 。对于连接装置的力与变形来说,方法 2 比方法 1 分别减小了 42.9% 和 20% 。
Table 4 Comparison of non-uniform seismic reduction response
表 4 非一致减震反应比较
| 位 置 | 分 量 | 漂浮体系 | 方法一 | 方法二 |
|---|---|---|---|---|
| 塔梁连接装置 | 力(kN) | / | 2.1e7 | 1.2e7 |
| 变形(m) | / | 0.75 | 0.60 | |
| 塔底 | 剪力(kN) | 2.5e7 | 2.0e7 | 1.8e7 |
| 弯矩(kN.m) | 1.9e9 | 1.3e9 | 1.5e9 | |
| 梁端 | 位移(m) | 1.23 | 0.78 | 0.65 |
| 塔顶 | 位移(m) | 1.29 | 0.81 | 0.69 |
从上面比较中可以看出,在脉冲非一致地震动输入情况下,方法 2(黏滞阻尼器) 的减震效果不如在一致地震动输入情况下的明显4,对塔底弯矩的减震效果甚至不如方法 1(弹性连接)。究其原因是,非一致输入的相干性加强了关键构件的地震反应,使得黏滞阻尼器的减震效果减小。更大跨径的斜拉桥,在脉冲非一致地震动输入下的减震设计,可能需要另寻它法。
6 结语
(1) 混合场地以及较低的视波速条件下的脉冲非一致地震动输入,为该类型桥梁的最不利工况。
(2) 非一致地震动输入下,增大弹性连接的刚度,可以减小梁端位移,但是塔底弯矩和剪力变化比较起伏。
(3) 非一致地震动输入下, 随阻尼参数 $C$ 的增加, 位移反应均减小; 对于塔底弯矩和剪力, 反应先减小, 然后略微增大, 后接近平稳。与一致地震动输入相比, 反应最低值在参数 $C$ 较大时达到。另外, 速度指数 $\alpha$ 的增大, 会减小反应值。
(4) 在脉冲非一致地震动输入下,黏滞阻尼器的减震效果改善得不明显,对塔底弯矩的减震效果甚至不如弹性连接。
(5) 近断层处修建更大跨径的斜拉桥,其在脉冲非一致地震动作用下的减震设计,可能需要另寻它法。
参考文献:
刘启方, 袁一凡, 金星, 等. 近断层地震动的基本特征 [J]. 地震工程与工程振动, 2006, 26(1): 1-10. LIU Qifang, YUAN Yifan, JIN Xing, et al. Basic characteristics of near-fault ground motion [J]. Earthquake Engineering and Engineering Dynamics, 2006, 26(1): 1-10. (in Chinese) ↩
李小军, 贺秋梅, 元兴军. 地震动速度脉冲对大跨斜拉桥减震控制的影响 [J]. 应用基础与工程科学学报, 2012, 20(2): 272-285. LI Xiaojun, HE Qiumei, QI Xingjun. Seismic mitigation control effects of long-span cable-stayed bridges to ground motions with velocity pulse [J]. Journal of Basic Science and Engineering, 2012, 20(2): 272-285. (in Chinese) ↩
李勇,闫维明,陈彦江,等. 大跨斜拉桥的近断层地震响应及减震控制 [J]. 防灾减灾工程学报,2010,30(5):479-486. LI Yong,YAN Weiming,CHEN Yanjiang,etal. Seismic response analysis and control of long-span cable-stayed bridges under near-fault earthquakes [J]. Journal of Disaster Prevent and Mitigation Engineering, 2010,30(5):479-486.(in Chinese) ↩
韩振峰, 叶爱君. 千米级斜拉桥的纵向减震体系研究 [J]. 地震工程与工程振动, 2015, 35(6): 64-70. HAN Zhenfeng, YE Aijun. Research on the longitudinal earthquake-reduction system of cable-stayed bridges over kilometers [J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(6): 64 - 70. (in Chinese) ↩ ↩
刘逵. 大跨度斜拉桥非一致激励地震反应分析及减震设计 [D]. 成都: 西南交通大学,2010. LIU Kui. Seismic response analysis of long-span cable-stayed bridges under non-uniform excitation and aseismatic design [D]. Chengdu: Southwest Jiaotong University, 2010. (in Chinese) ↩
许春永, 元兴军, 宋国富. 行波输入下大跨斜拉桥减震控制分析 [J]. 工程抗震与加固改造, 2008, 30(6): 89-94. XU Chunyong, QI Xingjun, SONG Guofu. Analysis of seismic reponse control for long-span cable-stayed bridge under traveling wave input [J]. Earthquake Resistant Engineering and Retrofitting, 2008, 30(6): 89-94. (in Chinese) ↩
李维奇. 多向地震下大跨度斜拉桥非一致激励响应分析 [D]. 武汉: 华中科技大学, 2009. LI Weiqi. Seismic response analysis for long-span cable-stayed bridges under multi-dimensional and non-uniform excitations [D]. WuHan: Huazhong University of Science & Technology, 2009. (in Chinese) ↩
许莉,郑旭霞. 非一致地震激励下大跨斜拉桥的地震反应 [J]. 福州大学学报:自然科学版,2013,4(41):528-533. XU Li, ZHENG Xuxia. Seismic response of long-span cable stayed bridge under asynchronous excitations [J]. Journal of Fuzhou University: Natural Science Edition, 2013,4(41):528-533. (in Chinese) ↩
项海帆. 斜张桥在行波作用下的地震反应分析 [J]. 同济大学学报, 1983(2):1-9. XIANG Haifan. Earthquake response analysis of cable-stayed bridges under the action of travelling waves [J]. Journal of tongji University, 1983 (2):1-9. (in Chinese) ↩
秦权, 孙晓燕, 贺瑞, 等. 苏通桥对非一致地震地面运动的反应和人工波质量的讨论 [J]. 工程力学, 2006, 23(9):71-83. QIN Quan, SUN Xiaoyan, HE Rui, et al. Responses of sutong cable-stayed bridge to asynchronous earthquake ground motions and quality of synthetic time histories [J]. Engineering Mechanics, 2006, 23(9):71-83. (in Chinese) ↩
焦常科, 李爱群, 伍小平. 大跨双层斜拉桥的行波效应 [J]. 振动、测试与诊断, 2012, 32(4):553-559. JIAO Changke, LI Aiqun, WU Xiaoping. Influence of waves traveling on seismic response of double-deck long-span cable-stayed bridges [J]. Journal of Vibration, Measurement & Dianosis, 2012,32(4):553-559. (in Chinese) ↩
Kiureghian A D. A coherency model for spatially varying ground motions [J]. Earthquake Engineering & Structural Dynamics, 1996, 25 (1): 99 - 111. ↩
Harichandran R S. Estimation the spatial variation of earthquake ground motion from dense array recording [J]. Structural Safety, 1991, 10(1/2/3):219-233. ↩ ↩
Hao H, Oliverra C S, Penzien J. Mutiple-station ground motion processing and simulation base on SMART-1 array data [J]. Nuclear Engineering and Design, 1989, 111(3):293-310. ↩
Abrahamson N. 2000. Near-fault ground motions from the 1999 Chi-Chi earthquake [R] //US-Japan Workshop on the Effects of Near-field Earthquake Shaking. PEER Report 2002/02, San Francisco, California: Pacific Earthquake Engineering Research Center: 11-14. ↩
Yang Qingshan, Chen Yingjun. A practical coherency model for spatially varying ground motions [J]. Structural Engineering and Mechanics, 2000,9(2):141-152. ↩
ADINA. User's Guide [M]. Adina R&D, Inc., Watertown, MA, 1995. ↩
Fleming J F, Egeseli E A. Dynamic behavior of a cable-stayed bridge [J]. Earthquake Engineering and Structure Dynamics, 1980(8): 1-16. ↩
Abdel-Ghaffar A M. Cable-stayed bridges under seismic action, cable-stayed bridges recent developments and their future [M]. Elsevier Science Publisher, 1991. ↩
周国良, 李小军, 刘必灯, 等. 大质量法在多点激励分析中的应用, 误差分析与改进 [J]. 工程力学, 2011, 1(28):48-54. ZHOU Guoliang, LI Xiaojun, LIU Bideng, et al. Error analysis and improvement of large mass method used in multi-support seismic excitation ananalysis [J]. Engineering Mechanics, 2011, 1(28):48-54. (in Chinese) ↩
张喜刚, 陈艾荣. 千米级斜拉桥设计指南 [M]. 北京: 人民交通出版社, 2010:55-56. ZHANG Xigang, CHEN Airong. Design guidelines of cable-stayed bridge over
$1\mathrm{km}$[M]. Beijing: China Communications Press, 2010:55-56. (in Chinese) ↩