叶爱君1, 何健2
(1. 同济大学 土木工程防灾国家重点实验室, 上海 200092; 2. 上海市政工程设计研究总院 (集团) 有限公司, 上海 200092)
摘要:针对我国普遍采用的大跨度桩基桥梁,应用无限元 - 有限元土体边界、桩土面 - 面接触算法和显式求解技术,提出了场地 - 结构整体模型的地震反应分析方法。以一座主跨为 202.5\mathrm{m} + 300.0\mathrm{m} 的独塔斜拉桥为工程实例,构建了河谷场地 - 桥梁整体有限元动力模型,研究了二维河谷场地对该斜拉桥纵向地震反应的影响,分析了基础附近扰动场地震动的特点。结果表明,场地中不同河岸高度和二维土层分布会对主塔处地震动的短周期分量产生一定影响,对结构短周期振型产生的地震力有较大影响;扰动场的地震动中接近基础振动频率的分量得到了加强,和自由场的地震动有显著区别,但长周期的分量变化较小。
关键词:整体有限元模型;河谷场地;群桩基础;斜拉桥;地震反应
中图分类号:TU352
文献标志码:A
Seismic Analysis Method of Cable-stayed Bridges Based on Integrated Model
YE Aijun1, HE Jian2
(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. Shanghai Municipal Engineer Design Institute (Group) Co. Ltd., Shanghai 200092, China)
Abstract: Site-structure integrated models are established on the basis of the finite element-infinite element boundary technique, surface-to-surface contact algorithm and time-domain explicit analysis for a 202.5\mathrm{m} + 300.0\mathrm{m} single tower cable-stayed bridge with a group pile foundation. Research on the longitudinal seismic response of the bridge is made with the integrated model which focuses on the effect of valley site and the properties of the ground motion under soil-structure interaction. The results indicate that the shape of the valley and the two-dimensional soil layer will affect the short period component of the ground motion and the response of the structure. The soil-structure interaction strengthens the components of ground motion near the frequency of the pile foundation, while it has little effect on the components for a longer period.
Key words: integrated finite element model; valley site; group pile foundation; cable-stayed bridge; seismic response
大跨度斜拉桥大多建设在地形复杂的河谷场地之上,河谷的形状和二维土层分布会使得河谷场地的地震动在小范围内存在较大的差异,在地震时对桥梁产生非一致激励。我国桥梁普遍采用大型群桩基础,地震中强烈的桩土相互作用会对基础附近的土体产生扰动,改变它们的地震动特性。这些因素使得大跨度桩基桥梁真实的地震动输入难以获取。
目前已有大量研究表明二维场地会产生明显的非一致地震动分布,对结构的地震反应有一定影响1,2,3,4,5,6。在现行的抗震规范中,除欧洲规范考虑了地震动的空间变化性外,其余大多规范都是采用一致的地震动输入方式,一般都只根据主基础处的土层将复杂的工程场地简化为一维水平成层土场地7,忽略二维场地对结构地震反应的影响,这种方法对大跨度桥梁而言显然过于粗糙。而且在斜拉桥的抗震研究中,一般采用六弹簧模型、P - Y(力 - 位移)弹簧等简化模型来分析桩 - 土相互作用,较难真实反应地震中的桩土相互作用过程。
场地 - 结构整体有限元法是目前研究土 - 结构相互作用较为精细的方法,也越来越多地被各国学者采用。但由于整体有限元模型复杂的建模过程以及巨大的计算代价,该方法大多还只是应用于小型结构或局部基础的分析中8,9,10,11,12,13,14,15。
本文在现有研究的基础上提出了场地 - 结构整体模型的大跨度桥梁地震反应分析方法,并以一座独塔斜拉桥为工程实例,构建了河谷场地 - 桥梁整体动力模型,对河谷场地中不同河岸高度和二维土层分布进行了分析,研究了二维场地对桥梁地震反应的影响,同时也对扰动场地震动进行了分析。
1 场地—结构整体模型地震分析方法
1.1 无限元-有限元人工边界
对场地进行分析时,需要处理无穷远的边界问题,在有限元模型中必须人为地截取结构邻近区域的土体,对截断的边界进行人工处理,称为人工边界。ABAQUS 软件中的“无限元”16为场地人工边界的处理提供了一个较好的方法,此“无限元”单元根据 Zienkiewicz 提出的静力响应和 Lysmer 与 Kuhlemeyer 提出的动力响应研发的,并恰当地选择衰减函数来模拟半无限空间。它吸取了黏弹性边界的优点,克服了传统黏性边界存在的低频失稳问题,计算精度更高。此方法最突出的优点是无需涉及解析解表达式,使无限元成为有限元的一部分,可以给出统一的求解格式。而且无限元单元的设置也十分简单,非常易于操作。相关研究表明,采用无限元边界计算自由场地地震反应的结果和 SHAKE 程序基于波动理论计算的结果基本一致8,验证了无限元边界的精度。
1.2 土体阻尼和非线性本构
分析大型场地地震反应时除了考虑土体人工边界的辐射阻尼外,还必须考虑土介质自身的材料阻尼。本文采用经典的瑞利阻尼理论,根据场地的基频和土体的阻尼比来求解瑞利阻尼的质量系数和刚度系数。土体的阻尼比根据动力三轴试验测定,采用土体有效剪应变对应的阻尼比。在地震反应分析时,可采用等效线性化的方法来考虑土体的等效阻尼。
对于土体非线性本构,考虑到屈服面在子午面上为线性的模型对于各种算法及接触有较好的适用性,本文采用 Drucker-Prager 模型16,它的本构可以由 3 个应力不变量表示。屈服准则表达式为
式中:t 为偏应力参数;p 为平均应力;\beta 为线性屈服轨迹在 p - t 应力平面上的倾角,通常是材料的摩擦角;d 为材料的粘聚力。
1.3 桩-土接触算法
桩基和土体的连接方式是研究桩土相互作用的又一关键,大多研究都采用各种属性的弹簧来模拟桩周土体的特性,例如目前应用较多的P - Y曲线。本文采用较为精细的面 - 面接触算法来分析桩 - 土的变形和动力相互作用。接触其实是一种特殊的约束,它是不连续的,只有当两个表面相接触时,接触条件才成立。ABAQUS 提供了一种接触对的接触模拟方法,即定义分析过程可能的接触面,形成接触对,同时赋予该接触对接触本构关系16。
接触面之间相互作用的属性主要包含两个方面:一是接触面之间的法向行为,可以模拟桩 - 土接触面的脱空;另一个是接触面之间的切向行为,包括接触面之间的侧向滑移以及可能的摩擦作用,所以此接触可以考虑桩侧滑动摩擦力的耗能效应。采用此接触算法可以较真实地模拟桩侧面和桩底面与土体的动力相互作用。
1.4 动力显式求解技术
因为上述的整体有限元模型涉及了土体非线性本构以及桩土之间非线性动力接触行为,在时域范围内的求解代价是异常巨大的17。本文采用 ABAQUS 中强大的动力显式求解技术来分析这些非线性问题。动力显式求解方法避免了在每一增量步内进行迭代求解大型的线性方程组,而基于动力学中的广泛使用的中心差分法、Newmark 法等对时间进行差分,计算速度快,适合求解大型有限元问题;而且只要时间步长取得足够小,显式求解一般不存在收敛性问题,这使其更适于求解非常复杂的非线性接触问题;显式算法的数值计算过程也更易于并行计算,可以更佳发挥目前多核处理器计算机的并行运算功能。
1.5 地震动输入方式
场地 - 结构整体模型中包含了实际工程场地的有限元模型,场地模型在深度方向上应该达到基岩的位置,在对模型施加地震激励时,采用实际场地基岩的地震动,直接施加在场地模型底部的基岩处。通过在基岩处输入不同相位差的地震动激励可以考虑相应的行波效应。
2 场地—结构整体模型的构建
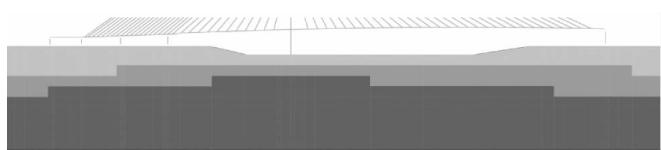
本文以一座主跨为 202.5\mathrm{m} + 300.0\mathrm{m} 的独塔双索面混合梁斜拉桥(图 1)为例构建场地 - 结构整体有限元动力模型。该斜拉桥采用半漂浮体系,结构主塔高 165.3\mathrm{m},桥面宽度 37.0\mathrm{m},主跨采用结合梁,辅助墩上的梁段采用混凝土梁。斜拉桥相邻的引桥是 30 米简支梁。
主塔基础采用 32 根直径为 2.6\mathrm{m} 的钢管桩,桩长 60.0\mathrm{m},每侧 16 根,4\times 4 矩形布置,桩间距 6.5m,承台高 6.0\mathrm{m},每侧重 16500\mathrm{t}。工程场地为河谷类型,河床宽 D 为 192.0\mathrm{m},河岸与河谷高差 H 为 7.5\mathrm{m},河谷场地的土层分布见图 2,土层性质见表 1。
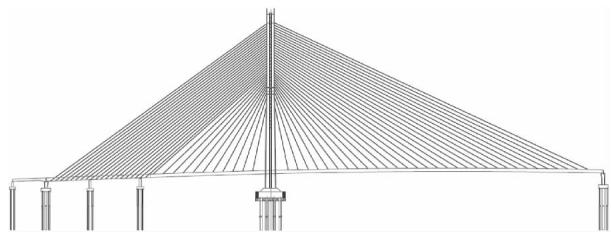
图 1 斜拉桥立面图
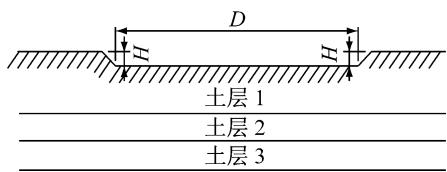
Fig.1 Elevation of the cable-stayed bridge
图 2 河谷场地剖面图
Fig.2 Profile of the valley site
表 1 主塔基础处土层性质
Tab.1 Properties of soils on the foundation of the major tower
| 土层 编号 | 厚度/ m | 弹性模 量/MPa | 密度/ (kg·m-3) | 粘聚力/ kPa | 摩擦角/ (°) |
| 土层1 | 10 | 399 | 2000 | 29 | 17.3 |
| 土层2 | 10 | 649 | 2050 | 35 | 18.0 |
| 土层3 | 70 | 3923 | 2050 | 53 | 18.0 |
应用场地 - 结构整体模型相关技术构建的河谷场地 - 桥梁整体有限元动力模型(图 3)共有 44001 个单元,57800 个节点。应用的计算机主频 3.2GHz,内存 2\mathrm{G},采用 4 核并行运算,计算 40~s 时程的时间为 10\mathrm{h}。本文选用的地震加速度时程为 1994 年北岭地震 24389 站点的实测数据,加速度峰值为 0.26g,卓越周期为 0.26s。

图 3 场地 - 桥梁整体有限元模型
Fig.3 Site-bridge integrated FE model
3 河岸高度的影响
实际工程中不同河谷的形态差别非常大,最为直观的差异是河岸与河床之间的高差 H(图 2),高差较小的河谷场地显得比较平缓,高差较大的河谷比较陡峭。这种差异可能会导致河谷场地的地震动分布有较大变化,因此本节对河谷场地的河岸高度 H 进行了参数分析。在不同的工况中分别考虑了 H 为 0, 7.5, 15.0, 20.0, 25.0m 这 6 种场地模型。
本节先对河谷场地自由场的地震反应进行了分析。从图 4 可以看出不同的河岸高度不仅影响了河岸地表的加速度峰值,而且对河床处的反应也有较大影响。随着河岸高度增加,河岸和河床上的加速度峰值都先增后减,而且河岸和河床上的地震动相差较大,呈现明显的不一致性。
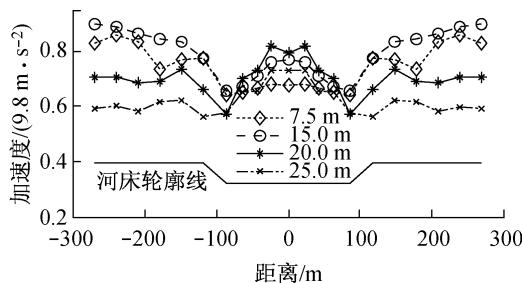
图 4 不同河岸高差下场地地表的加速度峰值(自由场)
Fig.4 Acceleration peak on the ground surface for different H (free site)
从图 5 可以看出河岸高度增加后河床中主塔基础处地表的加速度反应谱也有明显的变化。反应谱最大值对应的周期有所增大,这是由于河岸上覆盖层土层变厚,河谷场地的一阶周期有所增大。地震动频谱的变化主要集中在短周期范围内 (0.2 \sim 0.5 \mathrm{~s}),对于不同的河岸高差,地震动中 0.8 \mathrm{~s} 之后长周期的分量基本没有变化。
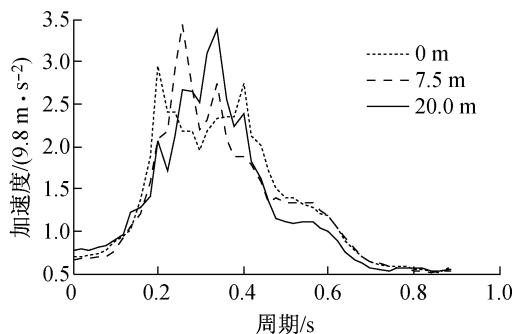
图 5 不同河岸高差下主基础处地表加速度反应谱
Fig.5 Surface acceleration spectra on the foundation of the major tower for different H
表 2 中的结果表明,随着河岸高度增加,结构的地震反应先增大后减小,和场地地表加速度峰值的变化规律相似。塔底弯矩的最大值出现在 H 为 7.5 \mathrm{m} 的工况中,比最小反应大 20\%;其他大多反应的最大值都出现在 H 为 20\mathrm{m} 的工况中。
表 2 不同河岸高度下结构地震反应最大值
Tab.2 Maximal seismic response of the structure for different H
| 河岸高 度/m | 塔底弯矩/ (MN·m) | 塔底剪 力/MN | 桩顶轴 力/MN | 桩顶剪 力/MN | 桩顶弯矩/ (MN·m) |
| 0 | 630 | 38.6 | 17.2 | 10.1 | 31.8 |
| 7.5 | 720 | 40.6 | 17.4 | 10.0 | 33.5 |
| 15.0 | 672 | 41.7 | 18.9 | 11.1 | 33.7 |
| 20.0 | 643 | 42.6 | 19.7 | 11.2 | 34.5 |
| 25.0 | 602 | 41.1 | 19.5 | 11.2 | 35.8 |
| 最大值/ 最小值 | 1.20 | 1.10 | 1.15 | 1.11 | 1.13 |
图 6 比较了河岸高度为 7.5\mathrm{m} 和 20.0\mathrm{m} 时塔底弯矩和桩顶剪力的频谱图。从图 6a 可以看出,河岸高度为 7.5\mathrm{m} 时,塔底弯矩在 1.5\sim 2.2\mathrm{Hz} 和 3.5\sim 4.5\mathrm{Hz} 范围的分量比高差 20.0\mathrm{m} 的反应要大,在 3.0\mathrm{Hz} 附近的分量略小,和图 5 中加速度反应谱的变化基本一致,整体上高差为 7.5\mathrm{m} 时塔底弯矩反应较大;但是对于桩顶剪力,它最敏感的频率是承台振动引起的频率,约在 3.0\mathrm{Hz} 附近,所以桩顶内力的最大反应出现在河岸高差为 20.0\mathrm{m} 的工况中。
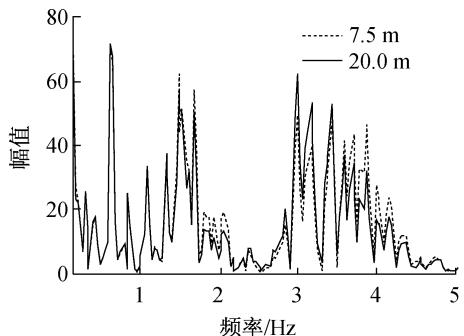
a 塔底弯矩
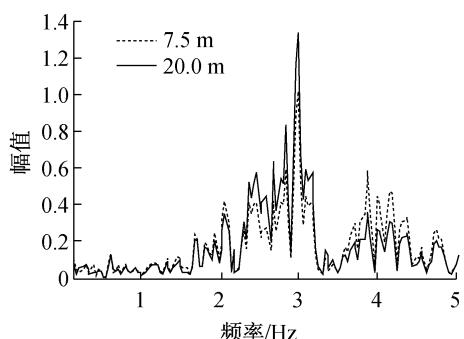
b 桩顶剪力
图 6 不同河岸高度下结构内力反应频谱图
Fig.6 Spectrogram of structure seismic response for different H
由以上分析可以看出,河岸高度对结构地震反应的影响较为复杂,与场地和结构的动力特性都有关,但变化主要产生在短周期的范围内(0.6\mathrm{s} 以内)。若控制结构反应的频率刚好在场地地震动变化较敏感的频率范围内,河岸高度会对结构的地震反应产生较大影响。
从表 3 可以看出河谷场地中河岸高度的变化对结构的地震位移反应也有一定影响,随着河岸高差增大,塔顶位移有增大的趋势,最大增加了 13\%,梁端位移先减小后增大,最大变化了 18\%,塔梁相对位移的变化较小。
表 3 不同河岸高度下结构地震位移反应最大值
Tab.3 Maximal seismic structure displacement for different H
| 河岸高度/m | 塔顶位移/m | 梁端位移/m | 塔梁相对位移/m |
| 0 | 0.172 | 0.123 | 0.131 |
| 7.5 | 0.174 | 0.122 | 0.130 |
| 15.0 | 0.188 | 0.104 | 0.130 |
| 20.0 | 0.193 | 0.110 | 0.132 |
| 25.0 | 0.195 | 0.118 | 0.134 |
| 最大值/ 最小值 | 1.13 | 1.18 | 1.03 |
4 二维土层分布的影响
河谷场地由于存在长期的泥沙冲刷和沉积作用,场地的土层在局部范围内往往有很大变化。在上文的模型中,虽然考虑了地表覆盖土层的河谷形状,但还是假定场地内部的土层都是水平的。本节将考虑场地中二维土层的分布,分析不同土层分布对结构地震反应的影响。
在实际场地中,靠近河床表面的两层土体剪切波速较小,是场地的软弱覆盖土层,本节将对这两层土的分布进行分析,在不同的工况中保持河床中主塔基础处的土层不变,分别设置软弱覆盖土层从河床到河岸逐渐变薄到 0\mathrm{m}、逐渐加厚到 40.0\mathrm{m} 以及土层倾斜的 3 种工况(图 7),分析此 3 种不同土层分布对场地地震动特性的影响。
从图 8 可以看出二维土层分布对河谷场地的地震动有较复杂的影响。软弱土层减小后(工况 1),河岸处加速度峰值显著下降,河床处的反应也略有减小;河岸软弱土层增大后(工况 3),河岸处的反应变化不敏感,但河床处的反应有所增大;倾斜的土层(工况 2)造成了整个河谷场地的地震动有更显著的差异,加速度峰值从覆盖层较薄的一侧河岸到较厚的一侧逐渐增大。
从主塔基础处地表的加速度反应谱(图 9)可以看出各种土层工况的地震动频谱特性有所区别,变化无明显规律,差异主要表现在短周期(小于 0.4\mathrm{s})的谱值,工况 3 反应谱峰值比水平土的反应略有增大,工况 2 和工况 1 的峰值略有减小。
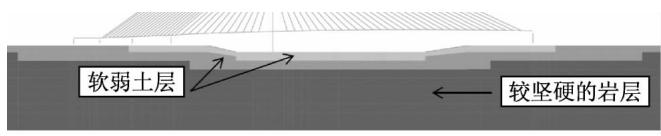
a 工况 1 (软弱土层变薄)
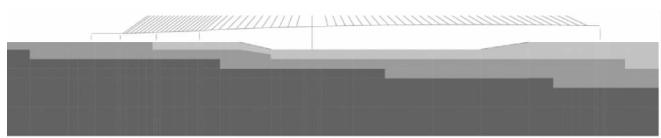
b 工况 2 (软弱土层倾斜)
c 工况 3(软弱土层变厚)
图 7 不同二维土层的计算模型
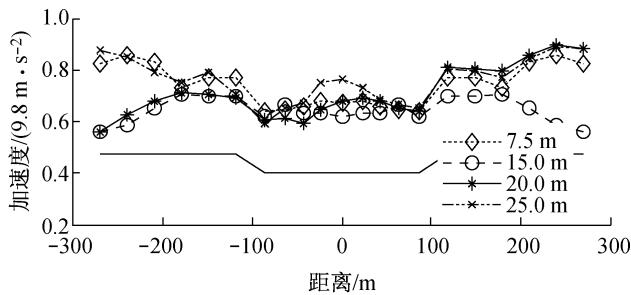
Fig. 7 Different models for 2-dimensional soil layers
图 8 不同土层分布下场地地表的加速度峰值(自由场)
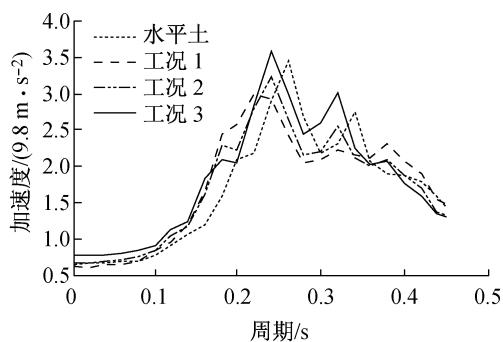
Fig.8 Acceleration peak on the ground surface for different soil layers (free site)
图 9 不同土层分布主基础处地表加速度反应谱
Fig.9 Surface acceleration spectra on the foundation of major towers for different soil layers
对于不同的土层工况,虽然主塔基础处的土层都是相同的,但是二维土层分布影响了主塔基础处的加速度峰值和地震动频谱特性。由此可以看出场地中某一点的地震反应不只是取决于该点处的土层特性,还和地震作用方向上二维土层的分布有关。
从表 4 可以看出,这 3 种工况使塔底内力的变化较大、桩基内力的变化较小,塔底内力的最大值出现在工况 3 中,最小值出现在工况 1 中,相差 27\%;剪力相差 20\%。
表 4 不同土层分布下结构地震反应最大值
Tab.4 Maximal seismic response of the structure for different soil layers
| 计算 模型 | 塔底弯矩/ (MN·m) | 塔底剪 力/MN | 桩顶轴 力/MN | 桩顶剪 力/MN | 桩顶弯矩/ (MN·m) |
| 水平土 | 720 | 40.6 | 17.4 | 10.0 | 33.5 |
| 工况1 | 618 | 35.5 | 17.0 | 9.9 | 31.6 |
| 工况2 | 651 | 36.7 | 16.9 | 9.6 | 30.7 |
| 工况3 | 787 | 42.6 | 17.6 | 9.9 | 32.4 |
| 最大值/ 最小值 | 1.27 | 1.20 | 1.04 | 1.01 | 1.06 |
从图 10 可以看出工况 3 的结构反应在 3.0\sim 4.2\mathrm{Hz} 范围的分量比工况 1 大,但在 2.5\mathrm{Hz} 附近的分量略小,和加速度反应谱的规律一致。因为塔底内力反应对频率 3.0\sim 4.2\mathrm{Hz} 范围的分量略敏感,对 2.5\mathrm{Hz} 附近的频率不敏感,所以工况 3 塔底弯矩比工况 1 大;但是从图 10b 可以看出,对于桩顶内力,这两个频率范围内增大和减小的分量相近,所以桩顶内力变化较小。
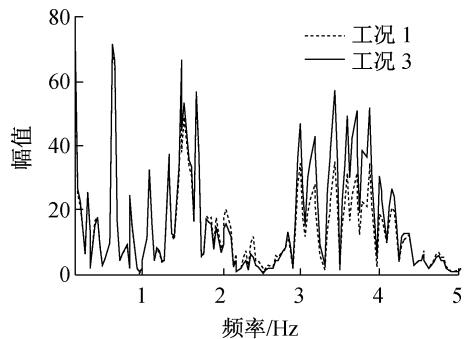
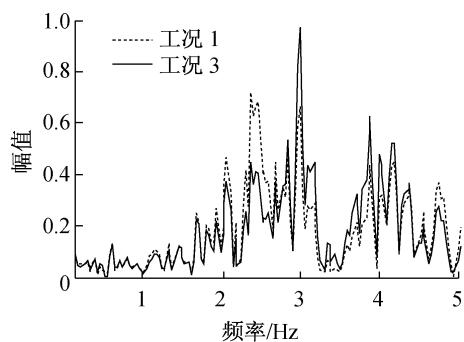
a 塔底弯矩
b 桩顶剪力
图 10 不同工况下结构内力反应频谱图
Fig. 10 Spectrogram of structure seismic response for different conditions
由表 5 可知,各土层工况下塔顶位移并不是很大,变化最为敏感的是过渡墩处的墩梁相对位移,工况 1 位移反应最小,比水平土工况的结果小 12\%,主桥和引桥的相对位移也减小了 8\%。
表 5 不同土层分布下结构地震位移反应最大值
Tab.5 Maximal seismic structure displacement for different soil layers
| 计算模型 | 塔顶位移/m | 过渡墩墩梁相对位移/m | 主桥与引桥相对位移/m |
| 水平土 | 0.174 | 0.131 | 0.157 |
| 工况1 | 0.168 | 0.116 | 0.144 |
| 工况2 | 0.170 | 0.118 | 0.147 |
| 工况3 | 0.175 | 0.119 | 0.146 |
5 扰动场的地震动分析
整体有限元模型中包含了结构基础附近的近场土体和距离基础较远的远场土体,能反应地震中群桩基础对场地的扰动作用。下文以水平成层土的场地 (H = 0\mathrm{m}) 为例,分析扰动场地震动的特点。
图 11 对比了结构的近场、远场和自由场地表处的加速度反应谱。近场以主塔桩基附近的土单元为代表,远场以纵向距离主塔基础 200\mathrm{m} 处的土单元作为代表,自由场为没有结构的场地。可以看出近场土体由于受到群桩基础的扰动作用,加速度反应谱和自由场有明显差别,反应谱中没有明显的平台段,而在周期为 0.40\mathrm{s} 处出现了一个绝对的峰值,这是由于承台的纵向振动周期为 0.41\mathrm{s},所以此处地震动分量得到了加强,而且因为场地的一阶周期也恰好在 0.40\mathrm{s} 左右,结构基础和桩周场地产生了共振效应,所以扰动场地震动的变化非常显著,但是远场地表的加速度反应谱和自由场基本相似,说明结构对较远处土体的扰动作用较小。
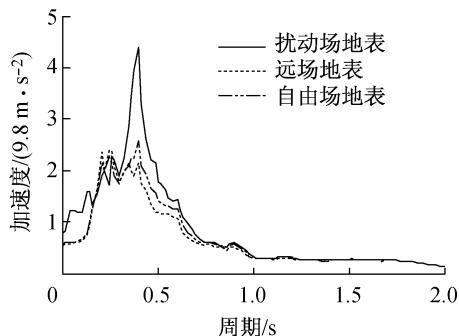
图 11 主基础处地表加速度反应谱
Fig. 11 Surface acceleration spectrum on the foundation of the major tower
实际上在近场和远场之间场地的地震动是逐渐变化的。图 12 显示了在承台内侧第一排桩纵轴线方向上场地地表加速度反应谱峰值的变化,承台下土体的反应明显偏大,最大比自由场增加了 112\%,在距离承台中心 10\sim 40\mathrm{m} 的范围内,扰动场的反应快速减小,土体到承台中心的距离超过 120.0\mathrm{m} 之后扰动场加速度反应谱峰值才和自由场的反应较一致。由此可见,随着土体到主塔基础纵向距离的增大,地表加速度反应谱峰值不断减小。
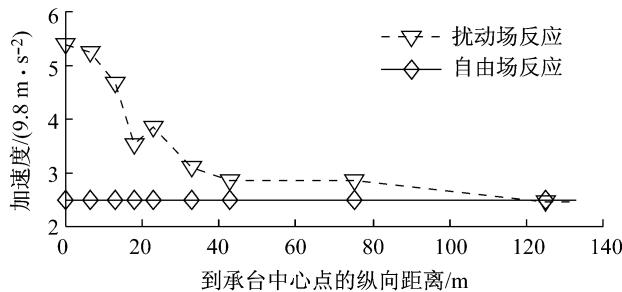
图 12 桩基纵轴线上场地地表的加速度反应谱峰值
Fig. 12 Surface acceleration spectrum peak at pile axes
6 结论
本文应用无限元 - 有限元人工边界、桩土面 - 面接触算法、显式求解方法等技术成功构建了大型场地 - 桥梁整体有限元动力模型,研究了二维河谷场中河岸高度和二维土层分布对桥梁地震反应的影响,并对扰动场的地震动进行了分析。结论如下:
(1)随河岸高度的增加,河床处加速度峰值先增大后减小,结构地震内力也有先增后减的趋势,产生了 20\% 左右的变化,塔顶位移增大 18\%。
(2)对于河谷场地中不同的二维土层分布,塔底内力最大产生了 27\% 的变化,边墩处的墩梁相对位移发生了 13\% 的变化。
(3)场地二维因素对结构地震反应的影响较为复杂,和场地以及结构的动力特性有关,但变化主要表现在地震动短周期的分量以及结构短周期振型贡献的地震力。
(4)扰动场的地震动和自由场有显著区别,桩侧土体的加速度峰值明显大于自由场的反应。距离主基础越近扰动作用越显著。扰动场地震动中接近基础振动周期的分量得到了加强,而长周期(0.6\mathrm{s} 之后)的分量变化很小。
参考文献
(上接第1325页)
[7] Lam W Y, Su R K L, Pam H J. Experimental study on embedded steel plate composite coupling beams [J]. Journal of Structural Engineering, 2005, 131(8): 1294.
[8] 吕西林, 陈云, 毛苑君. 结构抗震设计的新概念——可恢复功能结构 [J]. 同济大学学报: 自然科学版, 2011, 39(7): 941. LU Xilin, CHEN Yun, MAO Yuanjun. New concept of structural seismic design: earthquake resilient structures [J]. Journal of Tongji University: Natural Science, 2011, 39(7): 941.
[9] Fortney PJ, Shahrooz BM, Rassati GA. Large-scale testing of a replaceable “fuse” steel coupling beam [J]. Journal of Structural Engineering, 2007, 133(12): 1801.
[10] Chung H S, Moon B W, Lee S K. Seismic performance of friction dampers using flexure of RC shear wall system [J]. The Structural Design of Tall and Special Buildings, 2009, 18(7): 807.
[11] 膝军, 马伯涛, 李卫华, 等. 联肢剪力墙连梁阻尼器伪静力试验研究 [J]. 建筑结构学报, 2010, 31(12): 92. TENG Jun, MA Botao, LI Weihua, et al. Pseudo-static test for coupling beam damper of coupled shear wall structures [J]. Journal of Building Structures, 2007, 31(12): 92.
[12] 邓志恒, 林倩, 胡强, 等. 新型钢桁架连梁的抗震性能试验研究 [J]. 振动与冲击, 2012, 31(1): 76. DENG Zhiheng, LIN Qian, HU Qiang, et al. Test for aseismic behavior of new steel truss coupling beams [J]. Journal of Vibration and Shock, 2012, 31(1):76.
Elgamal A, Yan L, Yang Z, et al. Three-dimensional seismic response of Humboldt Bay bridge foundation-ground system [J]. Journal of Structural Engineering, 2008, 134(7): 1165. ↩
Zhang Y, Conte J P, Yang Z, et al. Two-dimensional nonlinear earthquake response analysis of a bridge-formation-ground system [J]. Earthquake Spectra, 2008, 24(2):343. ↩
Mayoral M J, Ramirez Z J. Site response effects on an urban overpass[J]. Soil Dynamics and Earthquake Engineering, 2011 (31): 849. ↩
Carbonari S, Dezi F, Leoni G. Seismic soil-structure interaction in multi-span bridges: application to a railway bridge [J]. Earthquake Engineering and Structural, Dynamics, 2011(40): 1219. ↩
Xu Jifeng, Bielak J, Ghattas O, et al. Three-dimensional nonlinear seismic ground motion modeling in basins [J]. Physics of the Earth and Planetary Interiors, 2003, 137:81. ↩
楼梦麟,范么清,叶爱君. 苏通大桥初设阶段主桥场地地震反应计算 [J]. 防灾减灾工程学报,2008, 27(4): 429. LOU Menglin, FAN Yaoqing, YE Aijun. Computation of site seismic response for Sutong Bridge in preliminary design phase [J]. Journal of Disaster Prevention and Mitigation Engineering, 2008, 27(4):429. ↩
Ashour M, Pilling P, Norris G. Lateral behavior of pile groups in layered soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130 (6): 580. ↩
金晶. 考虑冲刷效应的高桩承台基础地震反应分析 [D]. 上海:同济大学土木工程学院,2010. JIN Jing. Seismic response of elevated pile foundation of bridge with scour effects[D]. Shanghai: College of Civil Engineering of Tongji University, 2010. ↩ ↩
Yerli R H, Kacin S, Kocak S. A parallel finite-infinite element model for two-dimensional soil-structure interaction problems[J]. Soil Dynamic sand Earthquake Engineering, 2003, 23: 249. ↩
Kim K D, Yun B C. Time-domain soil-structure interaction analysis in two-dimensional medium based on analytical frequency-dependent infinite elements[J]. International Journal for Numerical Methods in Engineering, 2000,47:1241. ↩
Yerli R H, Temel B, Kiral E. Transient infinite elements for 2D soil-structure interaction analysis journal of geotechnical and geo-environmental engineering[J]. ASCE, 1998, 124(10): 976. ↩
Zheng Jingzhe, Takeda Tetsuo. Effects of soil-structure interaction on seismic response of PC cable-stayed bridge [J]. Soil Dynamics and Earthquake Engineering, 1995, 14:427. ↩
Balendra S. Numerical modeling of dynamic soil-pile-structure interaction[D]. Washington D C: Washington State University. ↩
Xu J, Costantino C, Hofmayer C, et al. Finite element models for computing seismic induced soil pressures on deeply embedded nuclear power plant structures[C]// ASME Pressure Vessels and Piping Division Conference. Vancouver: ASME, 2006: NUREG-76748-2006-CP. ↩
Doganguan A, Livaoglue R, Acar R. A study on seismic behavior of minarets considering soil-structure interaction [C]// International Earthquake Symposium Kocaeli. Izmit: [s.n.], 2007:393-404. ↩
Hibbitt, Karlsson, Sorensen. ABAQUS users manual [M]. 2004. ↩ ↩ ↩
Jeremic B, Jie G, Preisig M, et al. Time domain simulation of soil-formation-structure interaction in non-uniform soils [J]. Earthquake Engineering and Structural Dynamics, 2009 (38): 699. ↩