叶爱君, 刘伟岸, 王斌斌

（同济大学土木工程防灾国家重点实验室，上海 200092）

摘要：采用两质点模型近似模拟群桩基础和基础以上桥梁结构的动力特性，推导出桥墩、基础地震反应的计算公式，然后用数学工具 MATLAB 编制了一个程序，最后以一个实际结构为背景建立两质点模型进行了动力相互作用规律的探讨。结果表明，承台质量较大的高桩承台基础和基础以上桥梁结构之间的动力相互作用现象非常显著，计算桥墩和基础的地震反应时，承台质量的影响不可忽略，否则可能会引起很大的误差。

关键词：高桩承台基础；基础以上桥梁结构；动力相互作用；地震反应

中图分类号：U442.55

文献标识码：A

文章编号：0253-374X(2007)09-1163-06

Dynamic Interaction Between High-Rise Pile Cap Foundation and Bridge Structure

YE Aijun, LIU Weian, WANG Binbin

(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract: Based on a two-particle model approximately simulating the dynamic behavior of pile-group foundation and bridge structure above foundation, the formula calculating the seismic responses is derived, and programmed by MATLAB. Then a two-particle model with an actual structure as the background is established to study the dynamic interaction between the high-rise pile cap foundation and bridge structure. Study results show that, if the mass of a high-rise pile cap is large, there is a significant dynamic interaction between the pile foundation and bridge structure above foundation, so influence of the pile cap mass should not be ignored in the seismic responses analysis of pier and foundation, otherwise very great error may be caused.

Key words: high-rise pile cap foundation; bridge structure above foundation; dynamic interaction; seismic response

PDF BibTeX

群桩基础是建于软弱土层中的大跨度桥梁最常用的基础形式。而建于江海中的桥梁，广泛采用的是高桩承台基础，即部分桩身沉入土中，部分桩身露在地面以上或最大冲刷线以上的一种桩基结构形式。在桩基桥梁的地震反应分析中，业内已普遍认为应考虑群桩基础对桥梁地震反应的影响。于是很多学者对群桩基础的动力计算模型进行了研究，文献¹,²,³对各种实用的桩基计算模型进行了综述和研究。

一般认为，群桩基础的影响会使桥梁结构的周期变长，从而使结构的地震反应变小。我国现行的公路工程抗震设计规范⁴在计算桥梁结构的地震反应时，仅要求考虑桩基础的柔性，完全忽略了承台质量的影响。这在很多时候是合适的。但是在采用高桩承台基础的大跨度桥梁中，有一个很重要的特点值得特别关注，那就是桩基承台的质量往往很大，在桥梁的全部质量中占相当大的比例，有的甚至超过了一半。这往往是很难避免的，因为大跨度桥梁要求的基础桩数多，相应的平面尺寸和厚度就比较大，造成承台质量大。在这种情况下，桩基承台的振动效应就不能忽略。文献³曾指出，在极端情况下，当群桩基础 (桩身和承台) 的基本周期和基础以上桥梁结构（墩底固结）的基本周期相当时，会有基础以上桥梁结构和基础的动力相互作用问题，但文献³没有进一步对这种相互作用进行分析。

笔者针对大跨度桥梁中高桩承台的大质量问题，研究高桩承台基础与基础以上桥梁结构的动力相互作用，重点是动力相互作用规律的探讨。为了便于计算分析，以及更好地揭示高桩承台基础和基础以上桥梁结构的动力相互作用规律，本文选取较为简单的桥梁结构作为研究对象，如梁式桥，或其他体系桥梁中墩顶设滑动支座的桥墩。在这些桥梁结构中，桥墩的地震反应由一阶振型控制，可以简化为单质点体系进行地震反应计算，于是，高桩承台基础 - 基础以上桥梁结构体系就可以简化为两质点模型，可以方便地采用解析方法进行分析。

本文的基本思路是，采用两质点模型近似模拟群桩基础和基础以上桥梁结构的动力特性，推导出墩顶位移、墩底剪力和弯矩、承台底剪力和弯矩的计算公式，然后用数学工具 MATLAB 编制一个程序，最后以一个实际结构为背景建立两质点模型进行了动力相互作用规律的探讨，重点分析了群桩基础水平刚度和承台质量变化对基础以上桥梁结构和群桩基础地震反应的影响。

1 两质点模型及其地震反应公式的推导

1.1 两质点模型及自振特性

本文把高桩承台基础 - 基础以上桥梁结构体系简化为图 1 所示的两质点模型，其中，m_{1} 为等效的基础以上桥梁结构质量 (包括桥墩)，m_{2} 为承台质量，k_{1} 为墩身的水平抗推刚度，k_{2} 为群桩基础的水平刚度，l_{1} 为 m_{1} 形心到承台顶的距离，l_{2} 为单桩的等效嵌固长度，h 为承台厚度，P_{1} 和 P_{2} 分别为两质点产生的地震惯性力。其中，单桩的等效嵌固长度 l_{2} 所表示的含义是指长度为 l_{2} 的两端固结的杆件的水平刚度与实际桩基础中单桩的水平刚度相等，本文用 l_{2} 的变化来直观地模拟桩基础刚度的变化。

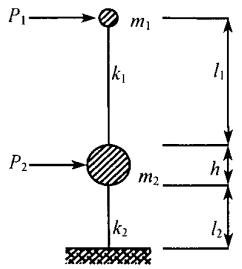
图 1 两质点模型
Fig.1 Two-particle model

两质点模型的两阶振型 (面内) 如图 2 所示，其中 \rho_{21},\rho_{22} 为振型坐标。两阶振型对应的自振频率由结构动力学的基本公式 \left|[K] - \omega^{2}[M]\right| = 0⁵求得

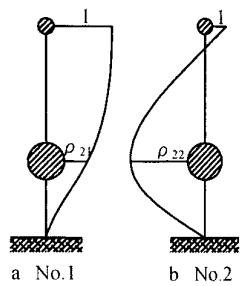
\begin{array}{l} \frac {\omega_ {1} ^ {2}}{\omega_ {2} ^ {2}} = \frac {1}{2} \left(\frac {k _ {1}}{m _ {1}} + \frac {k _ {1} + k _ {2}}{m _ {2}}\right) \bar {+} \\ \frac {1}{2} \sqrt {\left(\frac {k _ {1}}{m _ {1}} + \frac {k _ {1} + k _ {2}}{m _ {2}}\right) ^ {2} - 4 \frac {k _ {1} k _ {2}}{m _ {1} m _ {2}}} \\ \end{array}

\begin{array}{l} \rho_ {2 1} = \frac {k _ {1}}{k _ {1} + k _ {2} - \omega_ {1} ^ {2} m _ {2}} \\ \rho_ {2 2} = \frac {k _ {1}}{k _ {1} + k _ {2} - \omega_ {2} ^ {2} m _ {2}} \\ \end{array}

图 2 振型图
Fig.2 Vibration model

1.2 地震反应计算

本文采用反应谱方法计算两质点模型的地震反应，采用规范反应谱作为地震输入，振型组合采用平方和开方法 (SRSS)。根据多自由度系统反应谱计算的振型分解法¹，可得第 1,2 阶振型的振型参与系数 \gamma_{1},\gamma_{2} 分别为

\gamma_ {1} = \frac {m _ {1} + \rho_ {2 1} m _ {2}}{m _ {1} + \rho_ {2 1} ^ {2} m _ {2}}, \quad \gamma_ {2} = \frac {m _ {1} + \rho_ {2 2} m _ {2}}{m _ {1} + \rho_ {2 2} ^ {2} m _ {2}}

第 1 振型引起的两质点的最大地震惯性力分别为

P _ {1 1} = K _ {\mathrm {h}} \beta_ {1} \gamma_ {1} m _ {1} g, \quad P _ {2 1} = K _ {\mathrm {h}} \beta_ {1} \rho_ {2 1} \gamma_ {1} m _ {2} g

第 2 振型引起的两质点的最大地震惯性力分别为

P _ {1 2} = K _ {\mathrm {h}} \beta_ {2} \gamma_ {2} m _ {1} g, \quad P _ {2 2} = K _ {\mathrm {h}} \beta_ {2} \rho_ {2 2} \gamma_ {2} m _ {2} g

上述各式中：K_{\mathrm{h}} 为规范规定的水平地震系数；\beta_{1},\beta_{2} 为两阶动力特性对应的动力放大系数。

每个振型引起的墩顶位移 \Delta_{i}、墩底剪力 V_{i} 及弯矩 M_{i}、承台底剪力 V_{i}^{\prime} 及弯矩 M_{i}^{\prime}(i = 1,2) 分别为

\Delta_{i} = \frac{P_{1i} + P_{2i}}{k_{2}} + \frac{P_{1i}}{k_{1}} （忽略承台转角的影响）

V _ {i} = P _ {1 i}

M _ {i} = P _ {1 i} l _ {1}

V _ {i} ^ {\prime} = P _ {1 i} + P _ {2 i}

M _ {i} ^ {\prime} = P _ {1 i} \left(l _ {1} + \frac {h}{2}\right) + P _ {2 i} \frac {h}{2}

采用 SRSS 组合方法，便可求出各项地震反应

R _ {\max } = \sqrt {\sum_ {i = 1} ^ {2} R _ {i , \max } ^ {2}}

R 即为上面的 \Delta, V, M, V' 和 M'。

为了便于分析高桩承台基础和基础以上桥梁结构的动力相互作用规律，本文用数学工具 MATLAB 编制了一个程序，以画出结构各项地震反应随桩基刚度和承台质量变化而变化的规律。

2 高桩承台基础和墩身的动力相互作用分析

本文首先以苏通大桥 ( 主跨 1088\mathrm{m} 的钢斜拉桥 ) 的一个近塔辅助墩为背景建立两质点模型，分析高桩承台基础和桥墩的动力相互作用规律。辅助墩与主梁间设纵向滑动支座，且支座在恒载下所受竖向力很小，计算表明，滑动支座对桥墩地震反应的影响小于 6.7\%，因此该桥墩的纵向地震反应可忽略上部结构对墩的约束作用，而直接按单墩进行计算。该桥墩墩高 60~\mathrm{m}，纵向抗推刚度为 47080.37\mathrm{kN}\cdot\mathrm{m}^{-1}，根据规范⁴中动能相等原则把墩身等效为单质点，质点质量为 1084\mathrm{t}。由于防船撞设计的需要，高桩承台基础设计得相当强大，采用了 36 根 D2.8\mathrm{m} / D2.5\mathrm{m} 变直径钻孔灌注桩，承台质量为 38647t，考虑群桩基础刚度变化的影响，用单桩等效嵌固长度的变化来直观表达，于是群桩基础刚度为

k _ {2} = 3 6 \times \frac {1 2 E _ {2} I _ {2}}{l _ {2} ^ {3}} = \frac {3 9 1 0 4 6 4 0 0 0 0}{l _ {2} ^ {3}}

采用公路工程抗震设计规范⁴中四类场地反应谱作为地震输入。

2.1 高桩承台基础-桥墩的动力相互作用

对前述两质点模型，采用本文编制的 MATLAB 程序进行了地震反应分析，并通过变化群桩基础水平刚度来改变群桩基础的自振周期，以揭示高桩承台基础与基础以上桥梁结构的动力相互作用规律。同时建立等效嵌固桩长为一些特定值 (l_{2} = 2,5,10,\dots ,50\mathrm{m}) 的有限元模型，并将所算得的结果绘在同一张图上。

图 3a,b 分别绘出了墩顶位移和墩底弯矩随基础刚度变化的反应曲线，图中还同时绘出了桥墩 (墩底固结) 和群桩基础 (桩身加承台) 自振周期的变化曲线。从图中可以看出，由于承台质量的存在，桥墩的反应违反了单质点体系的地震反应规律（随着刚度的减小，位移单调增加，而弯矩单调减小），很醒目地出现了一个峰值，而这个峰值正好出现在桥墩和基础的自振周期相近的地方。这是由桥墩和承台的一种共振效应引起的。墩身的振动一部分是自身的振动，另一部分是承台振动引起的振动，随着等效嵌固深度的不断增加，当承台的自振周期和桥墩的自振频率相等时，桥墩跟承台产生共振，致使地震反应产生峰值。

图 3c,d 则显示了承台底剪力和弯矩随基础刚度变化的反应曲线，图中同样同时绘出了桥墩 (墩底固结) 和群桩基础 (桩身加承台) 自振周期的变化曲线。从图中可以看出，承台底剪力和弯矩的变化规律与桥墩的不同，表现得更加不规则，原因是承台底剪力和弯矩是由桥墩、承台两个质点的地震惯性力所贡献的，而不像墩底的剪力和弯矩只取决于桥墩质点的地震惯性力，从而产生的曲线是平滑的。为了解释这一不规则现象，图 4 绘出了两质点的地震惯性力随基础刚度变化的反应曲线。可见，前面所述的共振效应主要是影响桥墩质点的地震惯性力大小，而对承台质点的地震惯性力没多大影响。由于承台底的剪力主要取决于承台质点的地震惯性力，所以共振现象虽然出现在一个低谷处（第二振型两质点地震惯性力反向），但不明显；而承台底弯矩主要取决于桥墩质点的地震惯性力，所以有明显的共振现象。

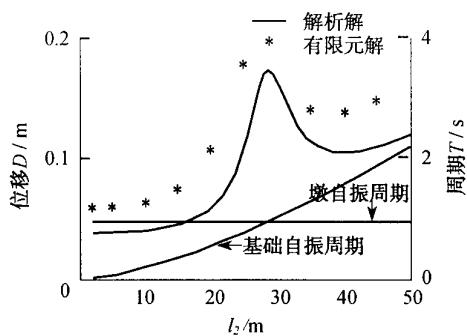
a 墩顶位移

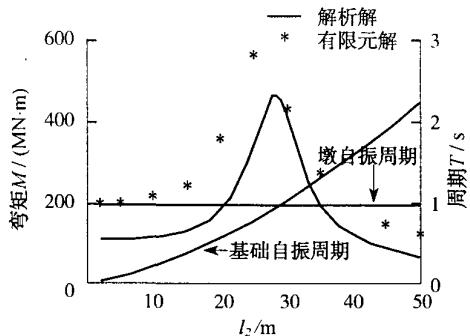
b 墩底弯矩

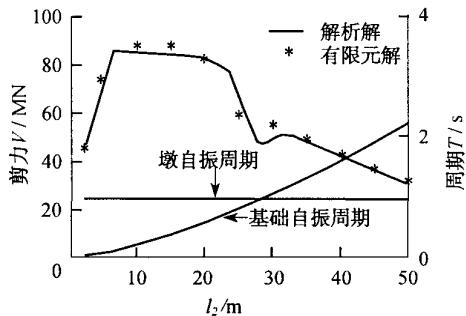
c 承台底剪力
图 3 桩基础刚度对桥墩及其基础地震反应的影响

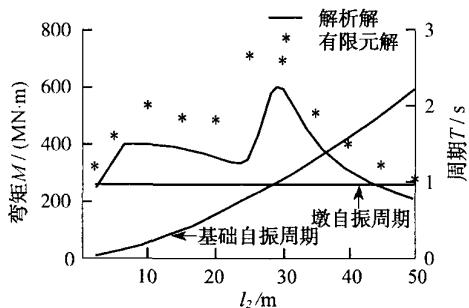
d 承台底弯矩
Fig.3 Effect of pile foundation stiffness on seismic responses of pier and its foundation

图 3 还表明，对于单墩的反应，解析解和有限元解有明显误差，但反映的高桩承台基础 - 桥墩的动力相互作用规律是一致的。

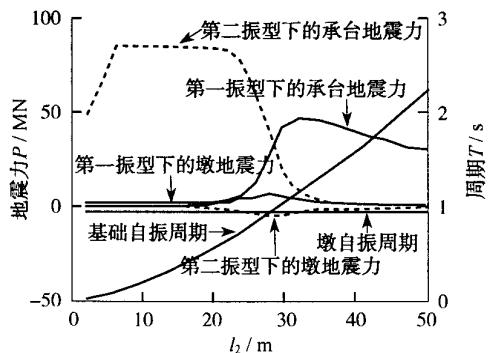
图 4 桩基础刚度对两个质点的地震惯性力的影响
Fig.4 Effect of pile foundation stiffness on inertia forces of two particles

2.2 承台质量对基础-桥墩动力相互作用的影响

为了进一步揭示高桩承台基础 - 桥墩的动力相互作用规律，本文特别关注了承台质量这一影响因素，通过改变承台的质量，分析承台质量的大小对各项地震反应的影响规律。分别令承台质量为 0, 1000, 5000, 10000, 20000, 50000 t, 对两质点模型进行地震反应计算, 墩顶位移、墩底弯矩、承台底剪力和承台底弯矩的反应曲线见图 5。

图 5 直观地显示了承台质量对高桩承台基础 - 桥墩动力相互作用的影响。可以看出，当承台质量小于桥墩质点质量时，没有明显的共振现象，然而随着承台质量的逐渐变大，才逐渐出现了高桩承台基础 - 桥墩的动力相互作用。对于桥墩的地震反应，承台质量越大，动力相互作用对结构反应的放大作用越大，但当基础的水平刚度很大时，动力相互作用对地震反应的影响均很小；对于基础的地震反应，当基础较柔时，承台质量越大，共振作用越明显，对反应的放大作用也越大，但当基础较刚时，虽然没有明显的共振现象，但承台质量直接影响了基础的地震反应，承台质量越大，基础的反应越大。

因此，对于承台质量较大的高桩承台基础，在计算桥墩和基础的地震反应时，承台质量的影响都是不可忽略的，否则可能会引起很大的误差。

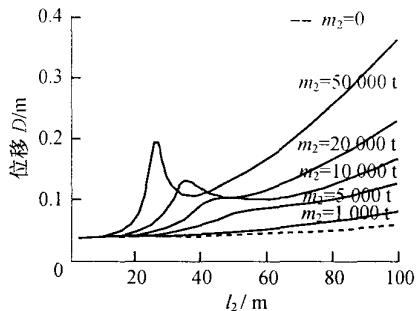
a 墩顶位移

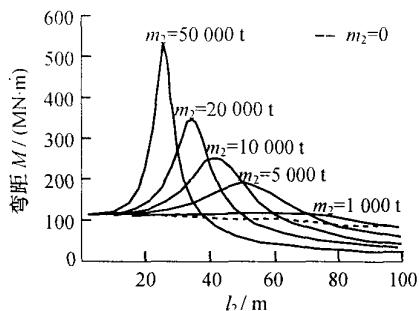
6 墩底弯矩

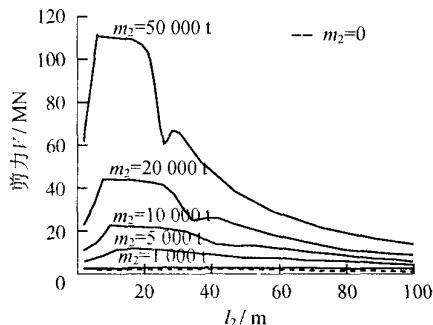
c 承台底剪力

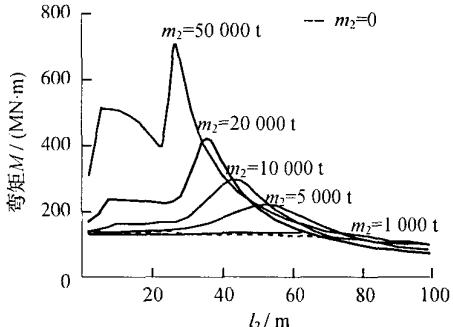
d 承台底弯矩
图 5 桩基础刚度和承台质量变化对桥墩及其基础地震反应的影响
Fig.5 Effect of pile foundation stiffness and pile cap mass on seismic responses of pier and its foundation

3 高桩承台基础和基础以上桥梁结构的动力相互作用分析

为了进一步探讨高桩承台基础和基础以上桥梁结构的动力相互作用规律，本文以一个实桥的设计方案，三跨双幅式连续钢梁桥（主跨 268\mathrm{m} 为例来进行分析。该连续梁桥的主墩墩高 38.4\mathrm{m}，墩顶设置固定支座，算得基础以上桥梁结构的等效质量为 12753.472t，墩身的抗推刚度 198329.82kN\cdot\mathrm{m}^{-1}，高桩承台基础也采用了 36 根 D2.8\mathrm{m} / D2.5\mathrm{m} 变直径钻孔灌注桩，承台质量为 38646t，群桩基础水平抗推刚度计算如前所述，并将前面所述的第四类场地反应谱作为地震输入。

图 6 画出了墩顶位移、墩底弯矩、承台底剪力和承台底弯矩随基础刚度和承台质量变化而变化的规律。在每个图中，6 条实线对应承台质量 m_{2} 分别为 0,1000,5000,10000,20000,50000t 时所反映出的规律，虚线对应的是实际连续钢梁桥方案通过 MATLAB 所得出的解析解，而离散点“*”对应的是实际连续钢梁桥方案通过有限元建模所得出的有限元解。可见，对于高桩承台基础和基础以上的桥梁结构，两质点模型解析解与有限元解反应的规律一致，而且误差较小。

图 6 同样表明，当承台质量很大的时候，高桩承台基础和基础以上的桥梁结构有很明显的共振现象，但是共振效应没有前面的更为突出，这是因为由于在前面的算例中，m_{2} 比 m_{1} 大很多 (35 倍之多)，而在这个算例中，m_{2} 比 m_{1} 大不了多少 (3 倍)。

这一算例同样表明，对于承台质量较大的高桩承台基础，在计算桥墩和基础的地震反应时，承台质量的影响都是不可忽略的，否则可能会引起很大的误差。

4 结论

本文采用两质点模型，用解析法对高桩承台基础 - 基础以上桥梁结构的动力相互作用进行了规律探讨，结果表明：

（1）承台质量小于基础以上桥梁结构等效质量时，一般不会出现基础 - 桥墩的动力相互作用现象。

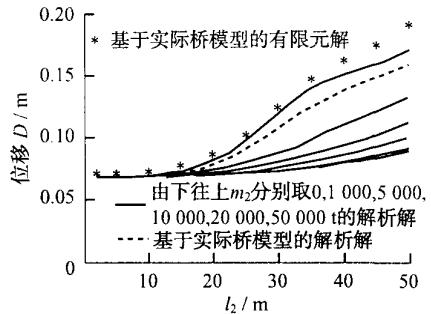
a 墩顶位移

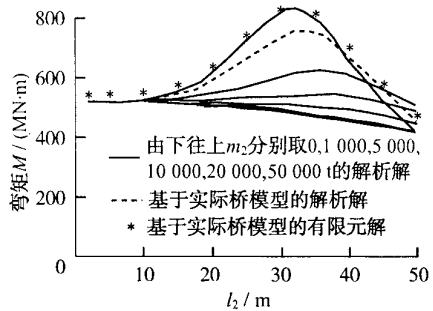
b 墩底弯矩

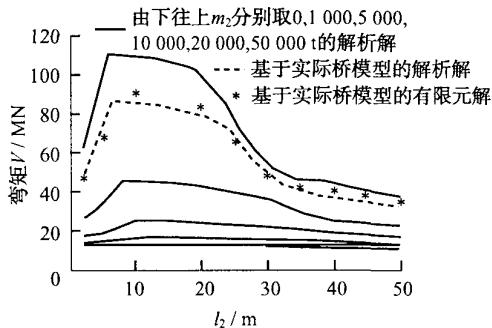
c 承台底剪力
Fig.6 Effect of pile foundation stiffness and pile cap mass on seismic responses of main pier and its foundation of a continuous girder bridge

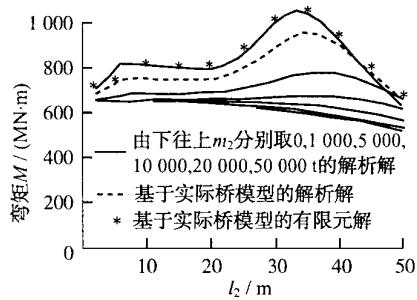
d 承台底弯矩
图 6 桩基础刚度和承台质量变化对连续梁桥及其基础地震反应的影响

(2) 承台质量较大时，桥墩的反应会表现出显著的共振效应，当桥墩和基础的自振周期相近时，会出现一个峰值，承台底剪力的共振效应不明显，但弯矩会出现明显的共振峰值。
(3) 对于承台质量较大的高桩承台基础，计算桥墩和基础的地震反应时，承台质量的影响不可忽略，否则可能会引起很大的误差。

参考文献：

（编辑：杨家琪）

范立础. 桥梁抗震 [M]. 上海：同济大学出版社，1997.
FAN Lichu. Seismic design of highway bridges[M]. Shanghai: Tongji University Press, 1997. ↩ ↩
范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计 [M]. 北京: 人民交通出版社, 2001.
FAN Lichu, HU Shide, YE Aijun. Seismic design for long-span bridges[M]. Beijing: China Communications Press, 2001. ↩
Ingham Tim J, Rodriguez Santiago, Donikian Roupen, et al. Seismic analysis of bridges with pile foundations[J]. Computers and Structures, 1999, 72:49. ↩ ↩ ↩
交通部公路规划设计院. JTJ004—89 公路工程抗震设计规范 [S]. 北京：人民交通出版社，1990.
China Highway Planning and Design Institute. JTJ004—89 Specifications of earthquake resistant design for highway engineering [J]. Beijing: China Communications Press, 1990. ↩ ↩ ↩
Clough R W, Penzien J. Dynamics of structures [M]. 2nd ed. New York: McGraw-Hill, 2001. ↩