沈星，叶爱君

（同济大学土木工程防灾国家重点实验室，上海 200092）

摘要

为研究大跨度斜拉桥倒 \text{Y} 型混凝土主塔横向破坏机理和弹塑性性能，选取典型大跨度倒 \text{Y} 型混凝土主塔斜拉桥，基于 \text{OpenSees} 非线性有限元平台，建立了考虑主塔弹塑性的非线性全桥有限元模型；以 3 组实测地震记录为地震动输入，采用动力增量分析方法（\text{IDA}）进行研究分析。研究结果表明：在不同实测地震动输入下，斜拉桥混凝土主塔横向屈服在横梁上侧截面，并由核心混凝土外侧钢筋拉应变控制，而破坏则在塔底或横梁上侧截面，并由核心混凝土外侧混凝土压应变控制；倒 \text{Y} 型混凝土主塔横向在地震中可形成 3 段塑性区域；斜拉桥混凝土主塔截面应考虑箍筋约束效应影响，该效应能明显增强混凝土主塔横向塑性性能，提高主塔横向抗震性能。

关键词

桥梁工程；斜拉桥；弹塑性分析；抗震性能

中图分类号：\text{U}448.27 文献标志码：\text{A}

Analysis on Lateral Seismic Performance of Inverted Y-shaped Concrete Tower for Long Span Cable-stayed Bridges

SHEN Xing, YE Ai-jun

(State Key Laboratory for Disaster Reduction of Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract

To research on lateral failure mechanism and elastic-plastic performance of the inverted Y-shaped concrete tower for long span bridges, a typical long-span cable-stayed bridge with inverted Y-shaped concrete tower was taken as the prototype, and based on \text{OpenSees} nonlinear finite element platform, a nonlinear finite bridge model, considering the main tower's elastic-plastic performance, was established. Three observed seismograms were taken as seismic input. Dynamic incremental analysis (\text{IDA}) was used to analyze. The results show that under different observed seismic inputs; the lateral yield in the concrete tower of cable-stayed bridge is found at the top section of the beam, which is controlled by tensile strain of reinforcement at the side of core concrete, while the lateral damage in the concrete tower is found at the top section of the beam or at the bottom section of the tower, which is controlled by compressive strain of concrete at the side of core concrete. For an inverted Y-shaped concrete main tower, three plastic zones are formed during the earthquake on the transverse direction. Confinement effect of transverse reinforcement in different sections of the main tower shall be taken into consideration, which can improve the lateral plastic performance and lateral seismic performance of the concrete tower.

Key words

bridge engineering; cable-stayed bridge; elastic-plastic analysis; seismic performance

PDF BibTeX

0 引言

据不完全统计，中国已修建各类斜拉桥 300 余座，是世界上修建斜拉桥最多的国家。由于抗震问题在早期大跨度斜拉桥的建设中并未受到足够的重视，导致其抗震设防标准较低，如上海南浦、杨浦大桥的设防地震重现期才 950 年。随着经济实力的增加，大跨度斜拉桥的抗震设防标准已逐步提高到 2500 年。由于各国的桥梁抗震设计规范普遍要求斜拉桥主塔在设计地震下保持弹性，因此，在进行斜拉桥抗震设计时，都只对桥梁弹性进行了地震反应分析和抗震验算。在纵桥向，由于中国普遍采用飘浮体系，而且不少大跨度斜拉桥的塔、梁间设置了黏滞液体阻尼器，因此主塔的纵向抗震性能比较好；而在横桥向，由于抗风的需要，主塔、主梁间普遍采用固定约束方式，造成主塔的地震力较大，因此斜拉桥主塔的横向地震力控制抗震设计。

中国现有斜拉桥的主塔横向抗震性能仅能满足抗震设防标准，当遭受更大地震时，主塔有可能会屈服并进入塑性工作状态。通过震害分析可知，在地震作用下斜拉桥主塔为易损构件，其他构件如主梁等都处于弹性状态，因此有必要研究斜拉桥混凝土主塔的横向弹塑性性能，以便评估现有桥梁在超过设防地震作用下的抗震性能。

各国学者均已意识到斜拉桥在强震作用下，可以利用主塔的弹塑性性能进行屈服耗能，以减少主塔底基础在强震作用下的地震响应，但是，目前对斜拉桥主塔在强震作用下的破坏机理并不清楚，对混凝土主塔横向进入非线性后的弹塑性性能研究尚属空白。美国塔科马海峡吊桥（悬索桥）允许主塔在 2500 年重现期（ 100 年超越概率 4\%）出现塑性区域，希腊里约 - 安蒂里奥大吊桥（斜拉桥）允许桥塔在 2000 年重现期（ 100 年超越概率 5\%）出现塑性区域。斜拉桥主塔的高塔身和高轴压比等特点使其可利用的延性相对于桥墩较小，因此不能采用目前普遍适用于常规桥墩的延性设计方法¹,²,³进行主塔的抗震设计。

若要在斜拉桥的抗震设计中利用主塔的塑性性能，必须对斜拉桥主塔的破坏机理和其在强震下进入非线性后的塑性性能进行深入研究，以便确定合理的性能目标。日本学者 \text{Endo} 等⁴建立单塔模型，采用 \text{Pushover} 分析方法，对主跨 2300\text{m} 悬索桥的钢桥塔进行了弹塑性性能研究。\text{Raheem} 等⁵通过对 1 座钢主塔斜拉桥运用非线性动力时程方法进行数值分析，并得出相关参数对斜拉桥钢主塔的影响。\text{Jones} 等⁶通过对新塔科马大桥钢主塔进行非线性时程分析，发现主塔在横向地震动输入时，下横梁和中横梁处的主塔截面开始进入塑性；而在纵向地震动输入时，主塔底部发生屈服。\text{Camara} 等⁷,⁸通过对 200\text{m}\sim 600\text{m} 跨径的斜拉桥进行推倒分析，以验证推倒分析方法在斜拉桥上的适用性。同济大学段听智⁹进行了强震作用下斜拉桥主塔纵向的振动台试验研究，并对中国典型混凝土主塔斜拉桥提出“桥塔有限延性设计”的抗震设计思想。同济大学焦驰宇¹⁰采用增量动力分析方法（\text{IDA}）对大跨度斜拉桥的纵向和横向进行全桥易损性分析，得出倒 \text{Y} 型主塔的易损性部位主要集中在下塔底、中塔底和中塔顶 3 个部位。

综上所述，国外学者研究的斜拉桥主塔主要是钢结构，中国所有大跨度斜拉桥主塔均为混凝土结构，材料的不同对主塔的弹塑性性能影响很大，并且混凝土主塔的弹塑性性能的不确定性更大。考虑钢筋混凝土结构采用实体单元进行动力计算时收敛性差，计算结果容易发散，因此一般采用纤维面单元研究其塑性性能。虽然目前没有对钢筋混凝土主塔进行拟静力推倒的试验研究，但是已有学者对高墩进行拟静力推倒试验，并采用 \text{OpenSees} 中的纤维面单元进行有限元模拟，证明纤维单元能够很好的模拟钢筋混凝土结构的塑性性能¹¹。

基于此，本文采用 \text{OpenSees} 非线性有限元平台，以 1 座典型大跨度斜拉桥倒 \text{Y} 型混凝土主塔为背景，建立考虑主塔弹塑性的动力分析非线性全桥有限元模型并以 3 组实测地震记录为地震动输入，采用增量动力分析方法（\text{IDA}），从混凝土主塔横向破坏机理、弹塑性性能等方面，揭示大跨度斜拉桥倒 \text{Y} 型混凝土主塔横向抗震性能。

1 有限元模型及地震动输入

以苏通长江大桥为背景桥梁，该桥为主跨 1088\text{m}，边跨 500\text{m} 的钢箱梁双塔斜拉桥；桥梁采用全封闭扁平流线型钢箱梁，全宽 40.6\text{m}，主梁中心线处高 4.0\text{m}；倒 \text{Y} 型混凝土主塔高 297.7\text{m}，下塔柱高 60.3\text{m}；索塔宽度顺桥向由塔顶 9\text{m} 变化至塔底 15\text{m}；横桥向塔顶宽 8\text{m}，向下逐渐变宽，中下塔柱横向宽度由分叉点处的 6.5\text{m} 变化至塔底的 8\text{m}。索塔材料采用 \text{C}50 钢筋混凝土。边墩包括近塔辅助墩、远塔辅助墩和过渡墩，墩身均采用分离的薄壁箱形空心墩，平面尺寸 8.5\text{m}\times 5\text{m}，墩高近 60\text{m}，墩身采用 \text{C}40 钢筋混凝土。与常规斜拉桥横向布置一样，主梁与主塔、边墩采用固定约束。考虑横向抗风需求，在塔梁间设置横向抗风支座来约束塔梁间的相对位移，因此在横向主塔只能依靠自身强度来抵抗地震荷载，这对主塔的横向抗震性能非常不利，并且该桥主塔在横向仅能满足预期设防地震（重现期 2500 年）作用下的抗震需求。

1.1 非线性有限元模型建立

本文研究对象为混凝土主塔，因此可从非主塔单元和主塔单元的有限元模拟这 2 方面来详细介绍有限元模型的建立方法。

1.1.1 非主塔单元模拟

在非线性有限元模型中，各主塔、墩底均固定约束，不考虑基础对全桥地震响应的影响。主梁、主塔中的横梁（内配有预应力筋）和塔柱分叉点以上索区部分是能力保护构件，即不允许其在地震中发生损伤，因此均采用弹性梁柱单元（\text{Elastic Beam Column}）模拟。主梁单元采用单主梁模型，需考虑主梁的质量和刚度。由于桥墩的横向地震响应对桥塔横向影响不大，因此桥墩也采用弹性梁柱单元模拟。斜拉索采用桁架单元（\text{Truss}）模拟，拉索面积从远塔索 0.012046\text{m}^2 变化到近塔索 0.004888\text{m}^2，并通过对拉索弹性模量折减来考虑拉索索垂度效应的影响¹²。拉索等效弹性模量 E_{\text{eq}} 为

E_{\text{eq}} = E / \left[1 + \frac{(\omega_0 l)^2 AE}{12 T^2}\right] \tag{1}

式中：E 为拉索的弹性模量；A 为拉索的截面面积；\omega_0 为拉索单位长度的重量；l 为拉索两端点的水平距离；T 为拉索拉力。

主梁、墩、主塔和拉索单元均考虑几何非线性效应（\text{P-Delta} 效应）。过渡墩、辅助墩和主塔纵向均采用滑动支座，力学模型均为弹塑性双线性模型。滑动支座水平力为摩擦力，即摩擦因数（0.02）乘竖向恒载；支座的弹性刚度由摩擦力除以摩擦位移（2\text{mm}）即可得到。已知过渡墩、辅助墩和主塔处的水平力分别为 50, 90, 138\text{kN}，刚度分别为 25, 45, 69 \text{MN}\cdot\text{m}^{-1}；墩、塔横向均采用固定支座，即刚度为无穷大。支座采用连接单元（\text{Two Node Link}）模拟，通过设置 3 个方向刚度来模拟支座的约束效应。

1.1.2 主塔单元模拟

本文主要研究混凝土主塔的横向弹塑性性能，由于倒 \text{Y} 型主塔分叉点上侧的索区段和横系梁在地震作用下保持弹性，因此主塔分叉点下侧的塔柱段采用基于力的非线性梁柱单元（\text{Nonlinear Beam Column}）模拟。倒 \text{Y} 型主塔分叉点下侧的单元由 4 种不同截面的纤维面单元组成，其分布及塔底纤维面内钢筋和混凝土布置如图 1 所示。

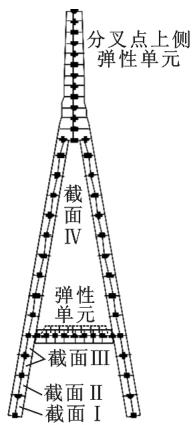
(a) 主塔单元布置

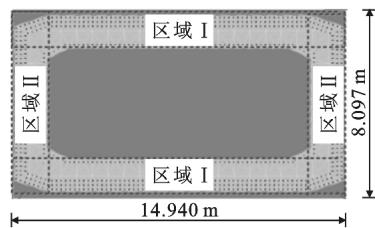
(b) 塔底纤维面内钢筋和混凝土布置

图 1 主塔单元和塔底纤维面布置

钢筋与混凝土本构关系决定其能否准确反映混凝土主塔横向弹塑性性能。在本文模型中，钢筋采用 \text{Steel}01 材料，该材料的本构关系为双线性，钢筋屈服强度为 400\text{MPa}，弹性模量为 200\text{GPa}，硬化率为 0.01。混凝土采用 \text{Concrete}01 材料，该材料未考虑混凝土的抗拉强度，其本构关系最先由 \text{Kent} 等¹³提出，后经 \text{Scott} 等¹⁴修正得到了修正 \text{Kent-Park} 模型。\text{Kent-Park} 模型的滞回规则简单，卸载线和再加载线重合，均是连接卸载点与残余塑性应变点的直线。\text{Kent-Park} 无约束混凝土的本构关系可以表示为¹¹

f = \begin{cases} f_{\text{cc}} \left[\frac{2\varepsilon}{\varepsilon_0} - \left(\frac{\varepsilon}{\varepsilon_0}\right)^2\right] & \varepsilon < \varepsilon_0 \\ f_{\text{cc}} [1-Z_1 (\varepsilon - \varepsilon_0)] \ge 0.2 f_{\text{cc}} & \varepsilon_0 \le \varepsilon \le 2\varepsilon_0 \\ 0.2 f_{\text{cc}} & \varepsilon > 2\varepsilon_0 \end{cases} \tag{2}

式中：f 为无约束混凝土强度；\varepsilon 为混凝土应变；f_{\text{cc}} 为混凝土圆柱体工后 28\text{d} 抗压强度；\varepsilon_0 为保护层混凝土开裂应变，\varepsilon_0 = 0.002；Z_1 为软化段斜率。

Z_1 表达式为

Z_1 = 0.5 / \left(\frac{145f_{\text{co}}}{3 + 0.29f_{\text{co}}} - 1000\right) \tag{3}

式中：f_{\text{co}} 为非约束混凝土抗压强度。

核心区约束混凝土骨架线的函数为

f_c = \begin{cases} K f_{\text{co}} \left[\frac{2\varepsilon}{\varepsilon_{\text{cc}}} - \left(\frac{\varepsilon}{\varepsilon_{\text{cc}}}\right)^2\right] & \varepsilon < \varepsilon_{\text{cc}} \\ K f_{\text{co}} [1-Z(\varepsilon - \varepsilon_{\text{cc}})] & \varepsilon_{\text{cc}} \le \varepsilon \le \varepsilon_{\text{cu}} \\ 0.2 K f_{\text{co}} & \varepsilon > \varepsilon_{\text{cu}} \end{cases} \tag{4}

f_{\text{cc}} = K f_{\text{co}}, \quad K = 1 + \rho_v f_{yh} / f_{\text{co}} \tag{5}

Z = 0.5 / \left(\frac{145f_{\text{co}}}{3 + 0.29f_{\text{co}}} - 1000 + 0.75\rho_v \frac{S_h}{h} - 0.002K\right) \tag{6}

式中：f_c 为核心区约束混凝土强度；\varepsilon_{\text{cc}} 为混凝土峰值应力时应变，\varepsilon_{\text{cc}} = 0.002K；K 为考虑约束引起的强度和峰值应变的增大系数；Z 为应变下降段的斜率；f_{yh} 是核心区箍筋的屈服强度；\rho_v 是横向约束箍筋的体积配筋率；h 为核心区混凝土宽度；S_h 为箍筋间距。

由于 \text{Kent-Park} 混凝土本构关系是基于大量实心矩形截面墩柱试验得出的经验公式，而本文中斜拉桥主塔为空心截面，因此并不能按全截面计算。本文将空心截面分成两部分，如图 1（b）所示，分别求出区域 I 和区域Ⅱ中实心截面约束混凝土相应参数，然后取极限强度和极限应变的较小值，从而保守考虑约束混凝土的弹塑性性能。保护层混凝土及 4 个截面内约束混凝土的本构参数如表 1 所示。

表 1 保护层混凝土和约束混凝土本构参数

混凝土类别	极限强度/\text{MPa}	极限强度时应变	极限应变时强度/\text{MPa}	极限应变
保护层混凝土	32.40	0.002 0	22.73	0.004 0
截面I约束混凝土	35.53	0.002 2	26.51	0.013 4
截面II约束混凝土	35.52	0.002 2	26.72	0.013 4
截面III约束混凝土	35.65	0.002 2	25.95	0.013 7
截面IV约束混凝土	35.14	0.002 2	26.82	0.012 2

研究主塔的非线性性能，必须考虑结构恒载作用。本文通过调整斜拉索初始应变，将索力调到成桥状态时的索力，以此来模拟成桥受力状态。最终，在模型中施加指定应变时索力与设计索力误差均在 1\% 范围内。模型中节点数为 392，主梁划分为 154 个弹性单元，主塔横梁为 8 个弹性单元，主塔分叉点上侧为 68 个弹性单元，主塔分叉点下侧为 72 个纤维单元，桥墩为 60 个弹性单元，每个单元设有等距的 10 个积分点。桥墩上设支座单元共 12 个，主塔处设支座单元 1 个。

1.2 地震动输入

为真实了解大跨度斜拉桥倒 \text{Y} 型混凝土主塔横向弹塑性性能，根据实际桥址场地类型，本文从太平洋地震中心数据库中以剪切波速小于 160\text{m}\cdot\text{s}^{-1}（四类场地）为基准，选取 3 组地震烈度较大的实测记录，分别为集集地震（编号：1494）、赫克托矿地震（编号：1801）和帝谷地震（编号：0170）。图 2(b) 为当地震动峰值加速度（\text{PGA}）调至 9.8\text{m}\cdot\text{s}^{-2} 时，3 条实测地震记录横向地震波的加速度时程，图 2(a) 为当 \text{PGA} 为 9.8\text{m}\cdot\text{s}^{-2} 时 3 条实测地震记录横向地震波对应 5\% 阻尼比时的加速度弹性反应谱以及保持横向地震波 \text{PGA} 和竖向地震波 \text{PGA} 比例不变时的 3 条竖向地震波对应 5\% 阻尼比时的加速度弹性反应谱。

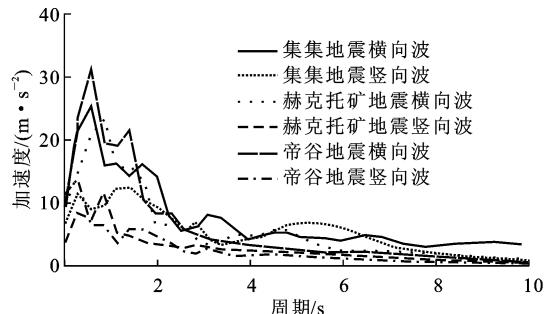
(a) 实测地震记录对应 5\% 阻尼比加速度反应谱

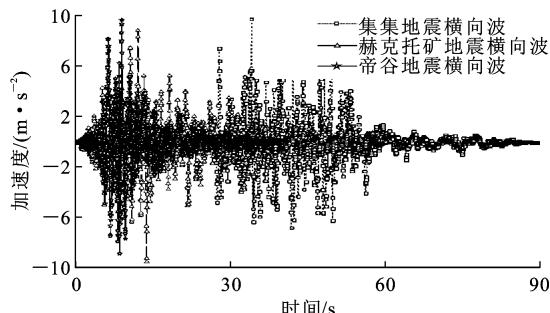
(b) 实测地震记录横向加速度时程

图 2 地震动输入

本文地震动输入采用横向加竖向组合，在调整地震动峰值加速度时保持原本地震记录横向与竖向比例不变。

2 混凝土主塔横向破坏机理分析

目前，研究考虑高阶振型影响的多自由度体系弹塑性性能的计算方法主要有模态推倒分析（\text{MPA}）和增量动力分析方法（\text{IDA}）。虽然 \text{IDA} 方法计算耗时长、收敛性差，但依然是目前研究结构非线性性能最准确的方法。本文基于 \text{IDA} 方法，通过调整 \text{PGA}，对结构进行非线性地震反应分析，以得到斜拉桥倒 \text{Y} 型混凝土主塔从弹性历经屈服进入非线性，直至达到最后破坏的弹塑性性能。截面曲率和截面内钢筋和混凝土应变是判别截面损伤程度的 2 个指标。本节主要从关键状态（屈服和破坏）下塔身曲率分布以及关键截面钢筋和混凝土最大应变随 \text{PGA} 变化 2 个方面来剖析混凝土主塔的横向破坏机理。

2.1 关键状态塔身曲率分布

曲率是从截面进行损伤判定，而应变是材料层面上的损伤判定。首先，从截面上可以较宏观地分析关键状态（屈服和破坏）下沿塔高的曲率分布，以了解混凝土主塔的横向破坏机理。在地震动输入过程中，倒 \text{Y} 型混凝土主塔 2 个塔柱横向截面内（同一主塔分叉点下侧 2 个塔柱，以下定义为左塔柱和右塔柱）会产生动轴力，动轴力对截面屈服时首次屈服曲率的影响较小，却对破坏时的破坏曲率影响较大¹⁰，因此本文以各截面在恒载轴力下的首次屈服曲率作为截面屈服状态的判定标准，通过截面内钢筋和混凝土应变是否达到极限应变来判定截面的破坏。图 3 为屈服和破坏状态下不同地震记录输入时沿塔身的曲率分布。

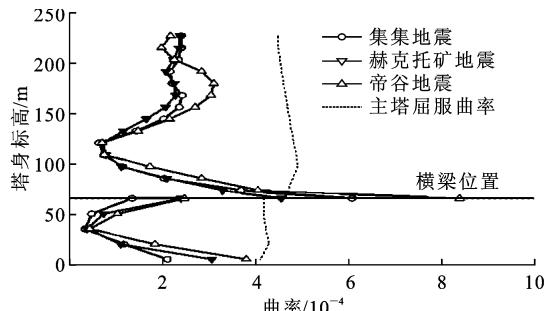
(a) 屈服状态曲率分布

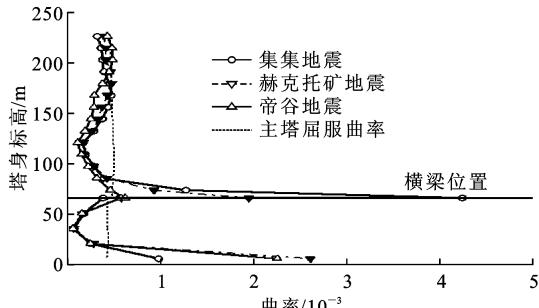
(b) 破坏状态曲率分布

图 3 关键状态曲率分布

由于左右塔柱在地震过程中承受的动轴力有差别，因此 2 个塔柱的受力状态有一定区别，图 3 给出了最不利塔柱关键状态的曲率分布。图 3(a) 中集集地震和帝谷地震对应的 \text{PGA} 均为 0.6g（g 为重力加速度），而赫克托矿地震对应的 \text{PGA} 为 0.8g。\text{PGA} 不一样的原因在于地震波的频谱不一样，主要取决地震波的频谱与结构横向特征周期的关系。由图 3(a) 可知：主塔横向均为横梁上侧截面首先屈服（屈服曲率为 0.00046），此时，塔底截面也即将达到屈服状态。图 3(b) 中集集地震和帝谷地震对应的 \text{PGA} 均为 1.2g，而赫克托矿地震对应的 \text{PGA} 为 1.6g。主塔在 3 组地震记录下发生破坏的位置并不相同，集集地震为横梁上侧截面首先破坏，而赫克托矿地震和帝谷地震均为主塔塔底截面首先破坏。

2.2 关键截面钢筋和混凝土最大应变随 \text{PGA} 变化

由图 3（b）可知：最不利截面位置为塔底、横梁下侧和横梁上侧截面。而主塔屈服都是由横梁上侧截面控制，破坏则分别由塔底截面和横梁上侧截面控制，因此图 4 给出了集集地震（横梁上侧截面控制破坏）和帝谷地震（塔底截面控制破坏）地震中 3 个关键截面的钢筋和混凝土最大应变随 \text{PGA} 的变化关系。

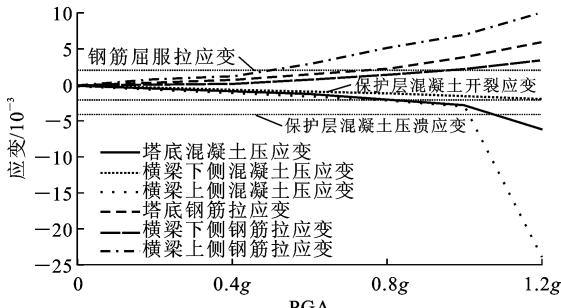
(a) 集集地震

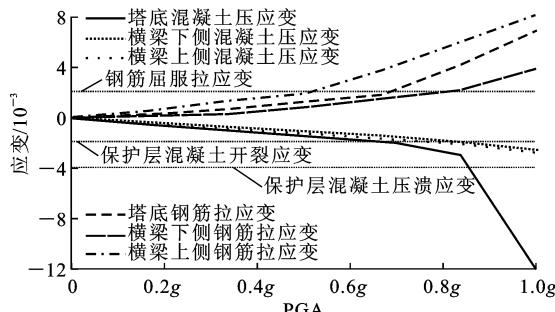
(b) 帝谷地震

图 4 关键截面钢筋和混凝土最大应变随 \text{PGA} 变化关系

由图 4 可知：横梁上侧截面屈服是由核心混凝土外侧钢筋达到屈服拉应变控制，随后塔底截面核心混凝土外侧钢筋也达到屈服拉应变，最后是横梁下侧截面核心混凝土外侧钢筋达到屈服拉应变。而破坏则是由核心混凝土外侧混凝土达到极限压应变控制。对于不同的地震记录，破坏的位置有所不同。集集地震是由塔底截面控制，而帝谷地震是由横梁上侧截面控制。最后破坏时，横梁下侧截面保护层混凝土均开裂，但未达到压溃应变（-0.004）。

3 混凝土主塔弹塑性性能分析

从主塔在不同地震记录下的塑性发展过程、不考虑箍筋约束效应对主塔横向弹塑性性能影响和关键截面破坏状态弯矩 - 曲率关系 3 个方面来剖析大跨度斜拉桥倒 \text{Y} 型混凝土主塔的横向弹塑性性能。

3.1 主塔塑性发展过程分析

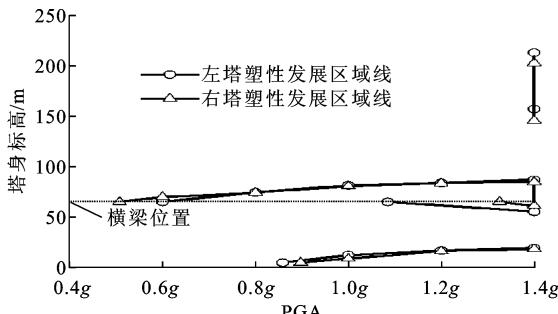
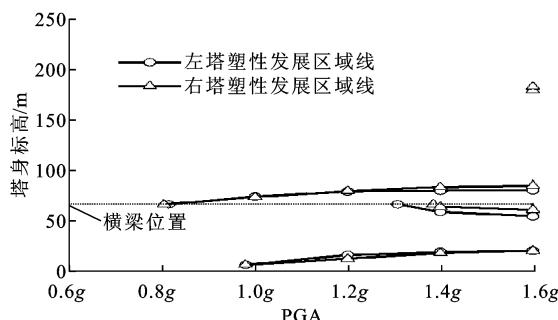
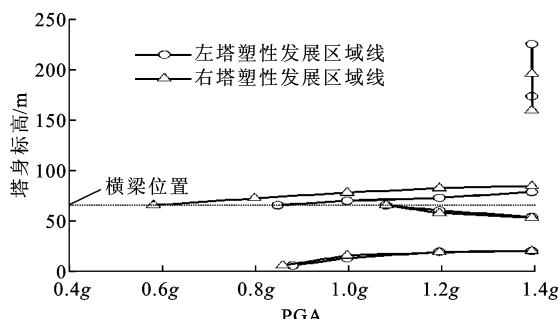
通过分析各截面应变沿塔身随 \text{PGA} 的变化趋势，可得到主塔分叉点下侧塔身各截面的塑性区域在不同地震记录下随 \text{PGA} 的发展过程，如图 5 所示。

(a) 集集地震

(b) 赫克托矿地震

图 5 主塔塑性发展过程

由图 5 可知：主塔分叉点下侧横向在不同实测地震记录下的塑性区域均可分为横梁上下侧、主塔底部、分叉点下侧 3 个部分。其发展过程为：首先是横梁上侧截面开始屈服，然后塑性向横梁上侧发展；紧接着主塔底部开始屈服，并随着 \text{PGA} 的增加开始向上延伸，形成塔底塑性区域；然后横梁下侧截面开始屈服，并随着 \text{PGA} 的增加开始向下延伸；最后当横梁上侧截面或塔底截面接近破坏时，在分叉点下侧区域内形成一段塑性区域（赫克托矿地震中左主塔并未形成），该区域虽然长度很长，但塑性发展程度并不大，不控制主塔横向破坏。

在集集地震中左塔塑性区域长度为 89.78\text{m} 占分叉点下侧区域范围的 40.65\%，右塔塑性区域长度为 78.76\text{m}，占分叉点下侧区域范围的 35.66\%；赫克托矿地震中，左塔塑性区域长度为 40.05\text{m}，占分叉点下侧区域范围的 18.13\%，右塔塑性区域长度为 41.31\text{m}，占分叉点下侧区域范围的 18.70\%；帝谷地震中，左塔塑性区域长度为 91.70\text{m}，占分叉点下侧区域范围的 41.52\%，右塔塑性区域长度为 82.26\text{m}，占分叉点下侧区域范围的 37.24\%。在同一地震作用下，左右塔塑性区域的不同主要是由地震过程中 2 个塔柱的动轴力差异所引起（2 个塔柱分别承受动轴拉、压力）。随着主塔非线性程度的加深，动轴力对塔柱刚度影响增大。对于不同实测记录，塑性区域长度的差异主要源于分叉点下侧形成的塑性区域段长度，而在横梁上下侧和塔底区域范围内，塑性区域长度差别不大。

3.2 箍筋约束效应对主塔横向弹塑性性能影响

以上分析均考虑箍筋对混凝土的约束效应，但由于主塔常采用空心截面，而混凝土本构试验是基于大量实心墩柱试验统计回归得到，同时，主塔仅考虑满足静力荷载，其截面内箍筋配筋率不高，因此需要对考虑与不考虑箍筋约束效应模型（将约束混凝土改为保护层混凝土）对主塔弹塑性性能的影响进行比较。图 6 为 2 种模型的基底剪力 - 塔顶位移关系。图 6 中，保护层混凝土不考虑箍筋约束影响；核心混凝土考虑箍筋约束影响。

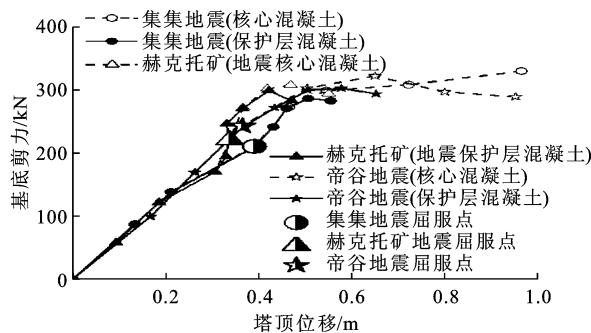
图 6 约束效应对基底剪力 - 塔顶位移的影响

由图 6 可知：主塔屈服前，主塔截面考虑与不考虑箍筋约束效应对基底剪力 - 塔顶位移并无影响。但当主塔进入非线性后，考虑箍筋约束效应的主塔塔顶塑性位移能力明显大于不考虑箍筋效应的主塔塔顶位移。由此可知，考虑箍筋约束效应能有效提高主塔横向延性能力。同时，如果提高主塔内箍筋配筋率，就能增强主塔的极限强度和极限应变，这样就能增强主塔的横向抗震性能，避免斜拉桥主塔横向发生脆性破坏。

3.3 关键截面破坏 \text{PGA} 时弯矩-曲率关系

本文第 3.2 节从构件方面分析主塔整体的弹塑性能，本节从截面方面探讨关键截面在破坏 \text{PGA} 状态时的弹塑性性能。由主塔横向破坏机理可知，最后破坏截面为塔底或横梁上侧截面。因此，下面通过集集地震（横梁上侧截面控制破坏）和帝谷地震（塔底截面控制破坏）在破坏状态时控制破坏截面的弯矩 - 曲率关系，分析关键截面的塑性性能，如图 7 所示。

图 7 关键截面破坏 \text{PGA} 状态弯矩 - 曲率关系

由图 7 可知：关键截面在破坏 \text{PGA} 状态的弯矩 - 曲率围成的滞回环较饱满，说明控制截面在地震过程中可通过自身进入塑性来消耗部分地震能量，以减少塔底基础的地震响应；同时，由于塔底截面的尺寸比横梁上侧截面大，其破坏曲率和破坏弯矩也比横梁上侧大，因此由塔底截面控制破坏的滞回环比由横梁上侧截面控制破坏的滞回环饱满，说明在塔底消耗的地震能量更大，对基础的保护作用更强。

4 结语

（1）在不同实测地震动输入下，斜拉桥混凝土主塔横向屈服在横梁上侧截面，由核心混凝土外侧钢筋拉应变控制；而破坏则在塔底或横梁上侧截面，由核心混凝土外侧混凝土压应变控制。
（2）倒 \text{Y} 型斜拉桥混凝土主塔横向在地震中可形成 3 段塑性区域，其发展过程为：首先横梁上侧截面屈服，继而沿塔身向上发展；然后塔底截面屈服，继而沿塔身向上发展；随后横梁下侧截面屈服，继而沿塔身向下发展；在主塔横向临近破坏时，在分叉点下侧区域形成非线性程度不大的塑性区域。

（3）斜拉桥混凝土主塔截面应考虑箍筋约束效应影响，其能明显增强混凝土主塔横向塑性性能，以提高主塔横向抗震性能。

（4）本文中研究内容揭示了斜拉桥倒 \text{Y} 型混凝土主塔的横向破坏机理和抗震性能，为斜拉桥后期混凝土主塔是否采用延性设计提供参考。由于本文内容主要基于有限元程序得到的数值分析结果，后期将针对全桥模型简化成单塔模型，然后对单塔模型进行拟静力试验，从试验方面进一步验证其破坏机理。

参考文献

\text{PRIESTLEY M J N}. \text{Performance Based Seismic Design}[J]. \text{Bulletin of the New Zealand Society for Earthquake Engineering}, 2000, 33(3): 325\text{-}346. ↩
\text{PRIESTLEY M J N, SEIBLE F, CALVI G M}. \text{Seismic Design and Retrofit of Bridges}[M]. \text{New York}: \text{John Wiley \& Sons, Inc}., 1996. ↩
范立础, 卓卫东. 桥梁延性抗震设计 [M]. 北京: 人民交通出版社, 2001. \text{FAN Li-chu, ZHUO Wei-dong}. \text{Ductility Seismic Design of Bridge} [M]. \text{Beijing}: \text{China Communications Press}, 2001. ↩
\text{ENDO K, KAWATOH C, UNJOH S}. \text{Analytical Study on Seismic Performance Evaluation of Long-span Suspension Bridge Steel Tower}[C]// \text{WCEE}. \text{Proceedings of the 13th World Conference on Earthquake Engineering}. \text{Vancouver}: \text{WCEE}, 2004:1\text{-}9. ↩
\text{RAHEEM S E A, HAYASHIKAWA T}. \text{Parametric Study on Steel Tower Seismic Response of Cable-stayed Bridges Under Great Earthquake Ground Motion}[J].\text{Structural Engineering/Earthquake Engineering},2003,20(1):25\text{-}41. ↩
\text{JONES M, TREYGER S, PENCE P}. \text{Seismic Analysis of the New Tacoma Narrows Suspension Bridge}[C]// \text{WCEE}. \text{Proceedings of the 13th World Conference on Earthquake Engineering}. \text{Vancouver}: \text{WCEE}, 2004: 10\text{-}24. ↩
\text{CASADO A C}. \text{Seismic Behaviour of Cable-stayed Bridges: Design, Analysis and Seismic Devices} [D]. \text{Madrid}: \text{Technical University of Madrid}, 2011. ↩
\text{CAMARA A, ASTIZ M A}. \text{Pushover Analysis for the Seismic Response Prediction of Cable-stayed Bridges Under Multi-directional Excitation} [J]. \text{Engineering Structures}, 2012, 41(3):444\text{-}455. ↩
段昕智. 强震作用下斜拉桥桥塔纵桥向振动台试验研究 [D]. 上海：同济大学，2012. \text{DUAN Xin-zhi}. \text{Experimental Study on Seismic Performance of Cable Stayed Bridge Tower Subjected to Longitudinal Strong Ground Motions}[D]. \text{Shanghai}: \text{Tongji University}, 2012. ↩
焦驰宇. 基于性能的大跨度斜拉桥地震易损性分析 [D]. 上海: 同济大学, 2008. \text{JIAO Chi-yu}. \text{Performance Based Seismic Fragility Analysis of Long-span Cable-stayed Bridges} [D]. \text{Shanghai}: \text{Tongji University}, 2008. ↩ ↩
罗征. 钢筋混凝土矩形空心墩抗震性能试验研究 [D]. 上海：同济大学，2012. \text{LUO Zheng}. \text{Experimental Study on Seismic Performance of Reinforced Concrete Columns}[D]. \text{Shanghai}: \text{Tongji University}, 2012. ↩ ↩
\text{THAI H T, KIM S E}. \text{Second-order Inelastic Analysis of Cable-stayed Bridges}[J]. \text{Finite Elements in Analysis and Design}, 2012, 53(6):48\text{-}55. ↩
\text{KENT D C, PARK R}. \text{Flexural Members with Confined Concrete}[J]. \text{Journal of the Structural Division}, 1971, 97(7): 1969\text{-}1990. ↩
\text{SCOTT B D, PARK R, PRIESTLEY M J N}. \text{Stress-strain Behavior of Concrete Confined by Overlapping Hoops at Low and High Strain Rates}[J]. \text{American Concrete Institute Journal}, 1982, 79(1): 13\text{-}27. ↩
\text{AHMED M A, MAGDI A K}. \text{Importance of Cable Vibration in Dynamics of Cable-stayed Bridges}[J]. \text{Journal of Engineering Mechanics}, 1991, 117 (11): 2571\text{-}2589.
\text{KOVAS I}. \text{Zur Frage der Seilschwingungen Under Seildampfung}[J]. \text{Bautechnik}, 1982, 59(10):325\text{-}332.
\text{YONEDA M, MAEDA K}. \text{A Study on Practical Estimation Method for Structural Damping of Stay Cables with Dampers} [C]// \text{Japan Society of Civil Engineers}. \text{Proceedings of the Japan Society of Civil Engineers}. \text{Tokyo}: \text{Japan Society of Civil Engineers}, 1989:455\text{-}458.
\text{UNO K, KITAGAWA S, TSUTSUMI H, et al}. \text{A Simple Method of Designing Cable Vibration Dampers of Cable-stayed Bridges}[J]. \text{Journal of Structural En-grg}, 1991, 37A: 789\text{-}798.
\text{PACHECO B M, FUJINO Y, SULEKH A}. \text{Estimation Curve for Modal Damping in Stay Cables with Viscous Damper}[J]. \text{Journal of Structural Engineering}, 1993, 119(6): 1961\text{-}1979.
\text{XU Y L, YU Z}. \text{Vibration of Inclined Sag Cables with Oil Dampers in Cable-stayed Bridges}[J]. \text{Journal of Bridge Engineering}, 1998, 3(4): 194\text{-}203.
\text{XU Y L, YU Z}. \text{Mitigation of Three-dimensional Vibration of Inclined Sag Cable Using Discrete Oil Dampers - II. Application}[J]. \text{Journal of Sound and Vibration}, 1998, 214(4):675\text{-}693.
\text{YU Z, XU Y L}. \text{Mitigation of Three-dimensional Vibration of Inclined Sag Cable Using Discrete Oil Dampers - I. Formulation}[J]. \text{Journal of Sound and Vibration}, 1998, 214(4):659\text{-}673.
\text{DUAN Yuan-feng}. \text{Vibration Control of Stay Cables Using Semi-active Magneto-rheological (MR) Dampers}[D]. \text{Hong Kong}: \text{Hong Kong Polytechnic University}, 2004.
廖小伟. 斜拉索 - 阻尼器系统数值分析与试验研究 [D]. 杭州：浙江大学，2012. \text{LIAO Xiao-wei}. \text{Numerical and Experimental Investigation on the Cable-damper System}[D]. \text{Hangzhou}: \text{Zhejiang University}, 2012.
周海俊, 孙利民. 斜拉索附加带刚度阻尼器的参数优化分析 [J]. 力学季刊, 2008, 29(1): 180-185. \text{ZHOU Hai-jun, SUN Li-min}. \text{Parameter Optimization of Damper with Stiffness for Stay Cable}[J]. \text{Chinese Quarterly of Mechanics}, 2008, 29(1): 180\text{-}185.