沈星^{1}, 倪晓博^{2}, 叶爱君^{1}
(1. 同济大学土木工程防灾国家重点实验室,上海 200092;2. 上海市政工程设计研究总院(集团)有限公司,上海 200092)
摘要
为了给大跨度斜拉桥边墩横向抗震体系设计提供依据,讨论了减震体系的合理性,并研究了减震体系的适用范围。首先,针对横向全滑动体系,分析了梁端横向位移的控制振型,推导了边跨主梁横向基本周期的简化计算公式,并利用反应谱法,推导与简化了地震下梁端横向位移的计算公式,通过与有限元计算结果对比,验证了其可靠性。然后,依据实际项目工程经验,通过合理简化与假定斜拉桥结构参数,在工程精度允许范围内,进一步对计算公式进行简化。最后,以主跨跨径与地震动输入为主要变量进行共计 384 个工况的计算,分析了各工况下梁端最大横向位移,得到了不同跨径下横向全滑动体系斜拉桥在不同场地类型与不同峰值加速度(\text{PGA})下的梁端最大横向位移变化规律。研究结果表明:以梁端横向位移为抗震目标时,对于Ⅲ、Ⅳ类场地,各 \text{PGA} 作用下,主跨跨径大于 400\text{m} 的斜拉桥均需考虑采用减震体系;对于 I、Ⅱ类场地,\text{PGA} 不大于 0.1g,主跨跨径不大于 600\text{m} 的斜拉桥可以不考虑采用减震体系;其中,如果结构的抗震能力大于地震需求,建议采用全限位体系;如果结构的抗震能力接近或小于地震需求,且梁端横向位移不控制时,则建议采用全滑动体系。
关键词
桥梁工程;大跨度斜拉桥;简化计算;抗震体系;边墩;横桥向
中图分类号:\text{U}448.27 文献标志码:\text{A}
Study on Seismic System of Side Pier of Long-span Cable-stayed Bridge in Transverse Direction
SHEN Xing^{1}, NI Xiao-bo^{2}, YE Ai-jun^{1}
(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. Shanghai Municipal Engineering Design Institute (Group) Co., Ltd., Shanghai 200092, China)
Abstract
To provide a reference for design of seismic system of side pier of long-span cable-stayed bridge in transverse direction, the rationality of seismic reduction system was discussed and the application scope of the system was mainly investigated. First, the controlling mode of the transverse displacement of the beam end was analyzed under the transverse sliding system, and the simplified calculation formula for fundamental period of the main girder of the side span was deduced. Response spectrum method was also used to derive and simplify the transverse displacement calculation of the beam end under earthquake. The reliability of the formula was verified by comparing its results with the finite element calculation results. Then, according to the experience of the practical engineering projects, the structure parameters of a cable-stayed bridge were reasonably simplified and assumed. Based on this, the calculation formula was simplified further within the allowable range of engineering precision. At last, 384 conditions in all were calculated by taking main span and ground motion as the main variables. The maximum displacements in transverse direction under respective conditions were analyzed and the change rules of the sliding system under different spans, site classifications and peak ground accelerations (\text{PGA}) were obtained. The results show that if the transverse displacement of the beam end is taken as the seismic performance objective, for III or IV site type, under any \text{PGA}, all cable-stayed bridges with main span larger than 400 meters need to use the seismic reduction system. For I or II site type, with the \text{PGA} less than 0.1g and the main span of a cable-stayed bridge less than 500\text{m} or 600\text{m}, there is no need to use the seismic reduction system. Thereinto, the fixed constraint system is recommended when the seismic ability of the bridge is greater than seismic demand; otherwise the sliding system is preferred when the beam end transverse displacement is not controlled.
Key words
bridge engineering; long-span cable-stayed bridge; simplified calculation; seismic system; side pier; transverse direction
0 引言
现有大跨度斜拉桥的抗震体系中纵桥向普遍采用飘浮体系,在塔、梁间设置了液压黏滞阻尼器,主塔纵向抗震性能较好;横桥向斜拉桥由于抗风需求,塔、梁间普遍采用固定约束方式。这种限位体系虽然主塔塔根处的横向地震内力很大,但由于静载和构造上的要求,塔根截面也很大,强度往往能满足要求。而对于斜拉桥边墩横向如采用限位体系,在地震作用下,桥墩和基础会产生超过其抗震能力的地震反应。中国抗震规范要求在罕遇地震下斜拉桥基础整体上保持弹性,边墩可按延性构件设计,以便震后快速修复。由于恒载作用下斜拉桥上部结构传递给边墩的压力较小,边墩桩基础的单桩数量有限,文献1中在斜拉桥的抗震性能研究中发现,在恒载与地震荷载共同作用下,边墩单桩可能会承受过大的拉力而成为拉弯构件,容易发生破坏,从而出现边墩墩柱尚未进入塑性状态而其基础的抗震能力严重不足的情况;另一方面,全限位体系要求支座在地震作用下不破坏,以保证其传力连续性,这需要对支座提出过高的抗剪要求。尤其对于大跨度斜拉桥,边墩支座承受地震力相当大,支座如果剪断,解除墩、梁间横向约束,相当于墩、梁间设滑动支座。这种全滑动体系虽然大幅度减小了传递到下部结构的地震力,但将产生相当大的梁端位移和墩、梁相对位移以及可能的残余位移2。因此,斜拉桥边墩横向抗震问题应引起关注。
在实际工程中,非减震体系或以牺牲力为代价,下部结构尺寸需设计较大;或以牺牲位移为代价,增大落梁风险。对于大跨度斜拉桥,在强震作用下,如果不耗减地震能量,只是被动地以构件自身承受地震荷载的结构体系,对结构本身及连接支座有过高的要求,并不是理想的抗震体系3。
随着减隔震装置的不断推广应用,边墩横向减震体系通过在滑动支座附近布置减震装置,利用减震装置发挥减震耗能作用,在保护桥梁下部结构强震作用下不受损伤的前提下,有效控制墩梁间横向相对位移,以实现边墩处力和位移的合理统一,是一种值得推广的大跨度斜拉桥边墩横向抗震体系7,8,9。针对边墩横向减震体系,一系列学者进行了研究。徐秀丽等4对大跨度斜拉桥横向局部减震体系进行了分析,提出近塔墩处采用横向黏滞阻尼器,其他墩处采用约束方案。冯云成等5,6提出在斜拉桥主梁与边墩之间设置横向黏滞阻尼器来控制大跨度斜拉桥的横向地震反应。沈星等7,9对大跨度斜拉桥横向减震装置与抗震设计方法进行了系统性研究。以上学者均只针对减震体系的合理性以及减震装置对斜拉桥横向抗震性能的影响进行研究分析,目前并没有对斜拉桥边墩横向采用减震体系的条件提出具体要求。
因此本文为合理应用斜拉桥边墩横向减震体系,研究了减震体系的适用范围,即明确适用减震体系的跨径特征和地震动参数,为桥梁工程师提供参考。为实现这一目标,首先将以斜拉桥主跨跨径作为变化参数,推导全滑动体系边墩横向周期简化计算方法;然后与位移反应谱结合,提出一种斜拉桥边墩横向全滑动体系梁端最大位移简化计算方法;最后得出不同跨径斜拉桥在不同地震动输入下的位移反应,并给出大跨度斜拉桥边墩横向合理减震体系的适用范围。
1 基本周期的简化计算
为应用反应谱理论简化计算全滑动体系的梁端横向位移,须首先解决梁端横向位移的控制振型问题,并根据控制振型的特征,模拟合理的形函数,以预估斜拉桥边墩横向全滑动体系的控制周期。
1.1 有限元模型与控制振型
本文首先利用 SAP2000 有限元程序,针对 4 座不同跨径大跨度双塔斜拉桥进行建模分析。
(1)模型模拟。主梁采用单主梁力学模型,通过主从约束与斜拉索相连;斜拉索、主梁和主塔考虑了恒载对几何刚度的影响;承台近似按刚体模拟,其质量堆聚在承台质心;墩底与承台中心及桩顶中心节点主从相连;基础用六弹簧模拟;二期恒载、横隔梁质量及边跨压重等附加质量以集中质量的形式加在梁单元上。
(2)边界约束条件。忽略相邻联对主桥的影响;塔梁之间的横向抗风支座仅在横桥向提供约束,不约束主梁绕竖向的转动;解除边墩处支座横桥向的约束,形成仅在竖向提供支撑的边墩全滑动体系。图 1 为边墩横向全滑动体系主要支座约束条件。图 1 中,X, Y 分别代表横桥向和竖桥向,边墩处双向滑动,主塔处仅在横桥向约束。
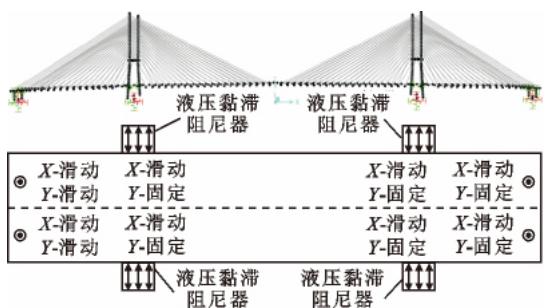
图 1 横向全滑动体系约束条件
(3)地震动输入。依据文献10(以下简称“规范”),选用特征周期 0.45\text{s},IV 类场地,抗震设防烈度 7 度 0.1g(g 为重力加速度),重现期为 2500 年的反应谱。计算前 500 阶振型贡献,振型组合采用 \text{CQC} 法,方向组合采用 \text{SRSS} 法。
表 1 为 4 座不同跨径斜拉桥横向振型信息。由表 1 可知:各桥前 3 阶横向振型均为主梁侧弯,其中横桥向第 1 阶振型如图 2 所示。根据反应谱分析计算得到的梁端横向地震位移,如果以 500 阶计算结果为基准,表 1 列出前 3 阶横桥向振型周期和每阶振型对应的累积贡献率。数据表明,梁端最大横向位移的控制振型以第 1 阶为主,贡献率达 82\%\sim 92\%,同时第 3 阶的贡献也不能忽略。
表 1 横桥向前 3 阶周期及每阶梁端横向位移累积贡献率
| 桥名 | 材料(梁/塔) | 主跨/\text{m} | 边跨/\text{m} | 振型阶数 | 周期/\text{s} | 梁端横向位移累积贡献率/\% |
|---|---|---|---|---|---|---|
| 赣江樟树二桥 | 钢混/混凝土 | 400 | 166.8 | 1 | 7.457 | 92.44 |
| 2 | 4.577 | 92.44 | ||||
| 3 | 2.059 | 99.95 | ||||
| 浙江某大桥 | 混凝土 | 620 | 295.0 | 1 | 14.658 | 91.52 |
| 2 | 9.583 | 91.52 | ||||
| 3 | 4.276 | 99.83 | ||||
| 芜湖二桥方案 | 混凝土 | 806 | 408.0 | 1 | 17.503 | 82.10 |
| 2 | 11.923 | 82.10 | ||||
| 3 | 5.679 | 98.84 | ||||
| 苏通大桥 | 钢混/混凝土 | 1088 | 500.0 | 1 | 33.800 | 88.37 |
| 2 | 20.621 | 88.37 | ||||
| 3 | 9.464 | 99.76 |

(a) 三维图

(b) 立面图

(c) 平面图

(d) 侧面图
图 2 横桥向第 1 阶振型:主梁侧弯
1.2 简化计算方法推导
文献11、12指出斜拉桥横向振动周期主要取决于主梁横向刚度,其模态可以简化为连续梁计算。通过对控制振型研究可知,大跨度斜拉桥边墩横向全滑动体系梁端最大横向位移贡献主要来自于主梁,影响主梁刚度的主要因素包括:主梁自身横桥向抗弯刚度、主塔下塔柱对主梁横向约束、主梁恒载轴力对几何刚度的修正、斜拉索对主梁几何刚度的约束效应。如果忽略地震作用下边墩墩顶对主梁的横向约束以及暂且忽略斜拉索的约束,将主塔下塔柱及基础的柔性用弹簧模拟,可得简化模型如图 3 所示。图 3 中 K_t 为主塔对主梁的约束刚度。
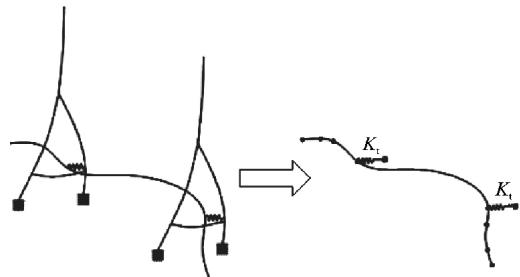
图 3 模型简化
为了较好地模拟 1 阶控制振型,可用反向均布荷载进行横向加载,如图 4 所示(图 4 中,\psi(x) 为横向变形;\psi_A(x) 为梁端 A 点处的横向变形,其他类似)。根据曲率与弯矩的关系、转角与曲率的关系、位移与转角的关系以及利用连续条件,最终得到形函数,其中边跨 AB 段与中跨 BE 段的形函数 \psi_{AB}(x) 与 \psi_{BF}(x) 如式 (1)、(2) 所示。
式中:L_p, L_s, L 分别为主跨跨长、边跨跨长、斜拉桥全长;q 为单位均布力;E 为材料弹性模量;I 为主梁横向刚度,其他类似。
经过试算发现,对于大跨度桥梁,主塔下塔柱及其基础对主梁的横向约束相对主梁自身刚度等不起控制作用,即 K_t = +\infty,可认为主梁在主塔处铰接。
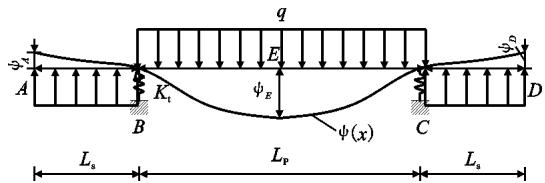
图 4 反向均布荷载作用下的变形
在得到形函数之后,根据结构动力学,不考虑阻尼力,有如下平衡方程
式中:Z(t) 为质点随时间 t 变化的横向位移;包含主梁均布质量 m(x) 与边跨处压重 M_{ti} 在内的主梁的广义质量 m^* 可表示为
式中:\psi_i 为第 i 个质点处横向变形。
主塔下塔柱柔性和主梁自身抗弯刚度的广义弯曲刚度 k_I^* 可表示为
如图 5 所示,斜拉索引起的主梁几何刚度 k_S^* 可表示为
式中:N_i 为第 i 个质点处的斜拉索索力;L_i 为相应索长。
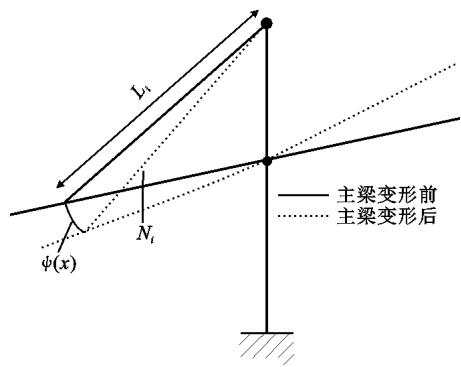
图 5 斜拉索的约束效应
如图 6 所示,恒载轴力引起的主梁几何刚度 k_G^* 可表示为
式中:N_{\max} 为主梁所受最大轴力。
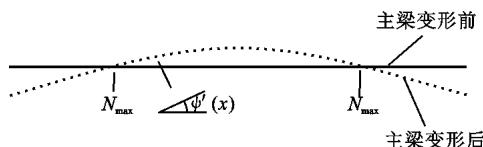
图 6 轴力作用下主梁横向变形
斜拉桥边墩横向全滑动体系横桥向控制振型周期 T 为
1.3 简化计算方法的验证
实际工程项目中,主梁的梁端、边墩、辅助墩附近等往往有压重,附加质量 M_{ti} 不可忽略。因此,在综合考虑斜拉索的约束效应、主梁恒载轴力对几何刚度的修正这些主要因素的基础上,按照上述公式可编程计算控制振型的周期。
为了验证简化计算方法的适用性,表 2 列出了控制振型的简化方法计算周期和有限元程序计算周期,并给出了误差。由表 2 可知,相对误差在 6\% 以内,表明简化方法的正确性与可行性。
表 2 控制振型周期简化计算公式校核
| 桥名 | 有限元的计算周期/\text{s} | 简化公式的计算周期/\text{s} | 相对误差/\% |
|---|---|---|---|
| 赣江樟树二桥 | 7.457 | 7.506 | 0.66 |
| 浙江某大桥 | 14.658 | 14.456 | 1.38 |
| 芜湖二桥方案 | 17.503 | 18.491 | 5.64 |
| 苏通大桥 | 33.800 | 33.585 | 0.64 |
2 梁端横向位移的简化计算
针对斜拉桥边墩横向全滑动体系,在得到梁端横向位移控制振型及其周期之后,可根据位移反应谱直接计算梁端位移。
2.1 简化计算方法
根据结构动力学,横桥向 j 阶振型的振型参与系数 \Upsilon_j 见式(9),即
式中:\Psi 为 \psi(x) 形成的列向量;u 为单位列向量。
根据单自由度系统的反应谱理论,梁端 A 点处横桥向第 j 阶振型的广义位移最大值 Y_{Aj}^{\max} 为
梁端 A 点处横桥向第 j 阶振型的结构位移最大值 u_{Aj}^{\max} 为
式中:S_a(T_j) 为第 j 阶阵型对应周期 T_j 的加速度反应谱。
2.2 简化计算方法的验证
根据加速度反应谱得到相应的位移反应谱,按照式 (9) \sim (11),得到简化公式梁端横向位移计算结果(记为 A')与有限元计算结果的比较见表 3。由表 3 可见:仅由第 1 阶横向振型计算得到的梁端位移均普遍比有限元计算结果偏小 20\% 左右。为了简化计算并减小误差,不再计算第 3 阶横向振型的贡献,而是在原简化计算公式基础上统一乘以放大系数 \beta=1.26,与有限元计算结果比较见表 3。
表 3 简化公式与有限元计算梁端横向位移结果比较
| 桥名 | 有限元计算位移/\text{m} | A'/\text{m} | A'_1/\% | \beta A'/\text{m} | A'_2/\% |
|---|---|---|---|---|---|
| 赣江樟树二桥 | 0.195 | 0.162 | 17.13 | 0.204 | 4.42 |
| 浙江某大桥 | 0.420 | 0.333 | 20.59 | 0.420 | 0.06 |
| 芜湖二桥方案 | 0.554 | 0.430 | 22.46 | 0.542 | 2.30 |
| 苏通大桥 | 0.884 | 0.681 | 22.97 | 0.858 | 2.94 |
注:A_1', A_2' 分别为 A', \beta A' 与有限元计算结果的误差。
3 大跨度斜拉桥的适宜抗震体系
为研究减震体系的适用范围这一问题,需要分析不同跨径斜拉桥在不同地震动参数条件下,全滑动体系的梁端最大位移。本节在第 2 节基础上,首先介绍结构合理参数假定,然后选用规范和实测地震记录为地震动输入,最后采用简化计算方法进行大量计算,给出大跨度斜拉桥边墩横向应用减震体系的合理范围。
3.1 结构参数假定
斜拉桥除主跨跨径以外的诸多参数将影响到梁端横向位移的计算,在改变主跨跨径这一关键参数的同时,其他参数将依据文献13,14中的经验给予合理的假定。以下将以自变量与因变量的方法对结构合理参数进行设定。其中:大跨斜拉桥主跨跨度 L_p 作为主要变化参数(自变量),边跨与主跨之比 L_s / L_p,m,M_{ti},EI,N_{\max},N_i 和索长 L_i,作为随 L_p 变化而变化的次要参数(因变量)。
具体设定为:① L_p 变化范围一般在 400\sim 1100\text{m},将 L_p 取离散值 400, 500, \ldots, 1100\text{m};② 2 L_s L_p^{-1} 变化范围为 0.27\sim 0.56,选取较大值 0.5;③ m(钢梁)变化范围为 18\sim 36\text{t}\cdot\text{m}^{-1},可选取代表值 20\text{t}\cdot\text{m}^{-1},M_{ti} 可以按照距梁端 0.4 L_s 的范围内以均布质量 m = 20\text{t}\cdot\text{m}^{-1} 计算;④ E 的材料属性统一为钢材,取 2.0\times 10^8 \text{kPa},I 取值为 80\sim 270\text{m}^4,图 7(a) 依据表 1 中大量工程数据绘出了刚度 I 随 L_p 的变化关系,可按照图 7 中拟合公式取值;⑤ N_{\max} 取值为 23\sim 215\text{MN},图 7(b) 依据表 1 中大量工程数据绘出了 N_{\max} 随 L_p 的变化关系,可按照图 7 中拟合公式取值;⑥ N_i 取值为 1700\sim 4600\text{kN},为简化计算,统一选取固定值 N_c = 3000\text{kN},L_i 可根据将斜拉索以 10\text{m} 索距沿主梁全长布置,主梁以上主塔高度取 L_p / 4.8 进行计算。
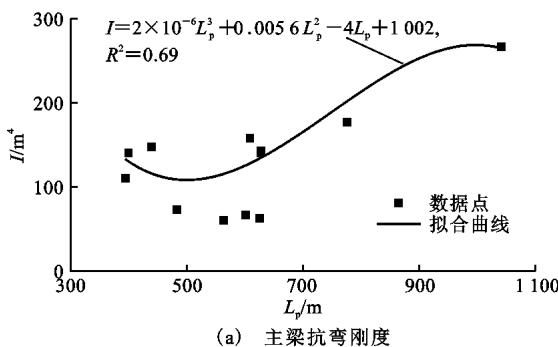
(a) 刚度 I 随 L_p 变化趋势
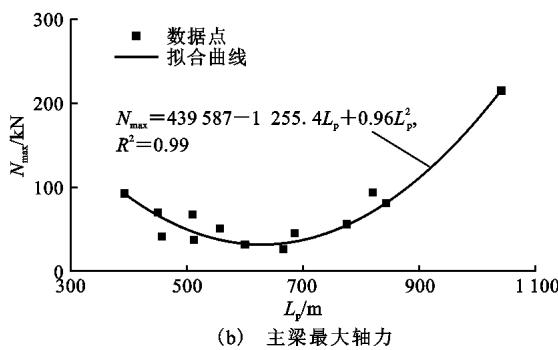
(b) N_{\max} 随 L_p 变化趋势
图 7 参数随主跨跨度变化趋势
采用上述结构假定的参数,以前述地震动参数作为输入进行梁端最大横向位移的计算。表 4 列出了进一步简化计算的结果与有限元计算结果的比较,相对误差在 15\% 以内,说明结构参数假定合理。
表 4 进一步简化计算的梁端横向最大位移与有限元结果对比
| 计算模型 | 主跨跨度/\text{m} | 有限元计算结果/\text{m} | 进一步简化计算结果/\text{m} | 相对误差/\% |
|---|---|---|---|---|
| 赣江樟树二桥 | 400 | 0.204 | 0.232 | 13.81 |
| 浙江某大桥 | 620 | 0.420 | 0.469 | 11.66 |
| 芜湖二桥方案 | 806 | 0.542 | 0.544 | 0.44 |
| 苏通大桥 | 1088 | 0.858 | 0.854 | 0.54 |
3.2 地震动输入
为考虑工程设计需求,本文选用规范反应谱作为地震动输入。其中规范反应谱:不同峰值加速度 P_{GA} = 0.1g,结构阻尼比 3\%,阻尼系数 C_d = 1.18 四类场地 I,Ⅱ,Ⅲ,Ⅳ的场地系数 C_s 均取 1.0。特征周期调整值 T_g 分别取 0.25, 0.45, 0.65, 0.90\text{s},并按照规范转换成对应的位移谱。图 8 为在阻尼比 3\%,P_{GA} = 0.1g 时规范 4 类场地加速度谱及其对应的位移谱。
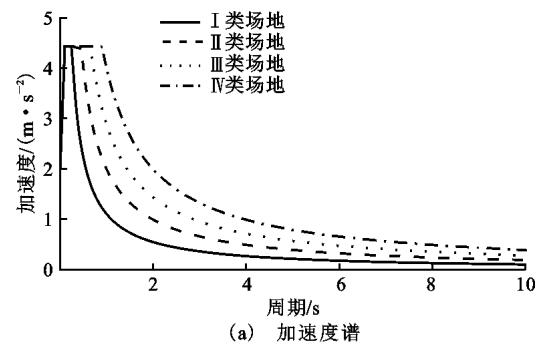
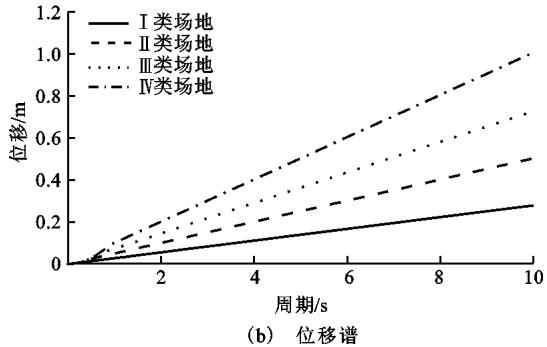
图 8 规范加速度谱与位移谱
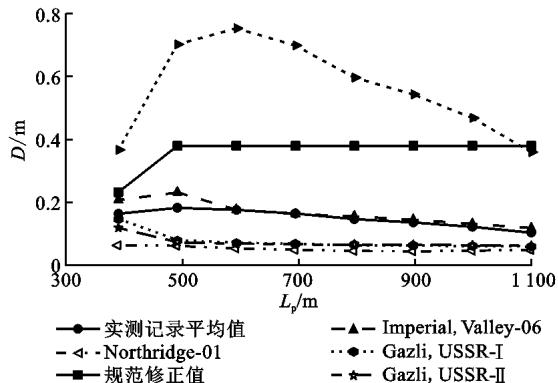
鉴于研究对象为大跨长周期结构,规范仅给出 10\text{s} 以内的加速度谱,10\text{s} 以后如继续延用,计算长周期结构的位移将会偏于保守15。现将 10\text{s} 之后的加速度谱以 1/T^2 速率下降,则得到位移谱在 10\text{s} 之后为平台段。图 9 为与上述加速度谱匹配良好的实测记录对应位移谱与规范修正谱的比较(图 9 中 D 为梁端最大横向位移)。其中所有地震波均从美国太平洋地震研究中心(\text{PEER})强震数据库中选取,每类地震波选 7 条,图 9 中为表达清楚,仅列出具有代表性的地震波。可以预测,规范修正谱计算结果总是能够大于实测记录平均值计算结果,且能够包络住绝大多数实测记录结果。
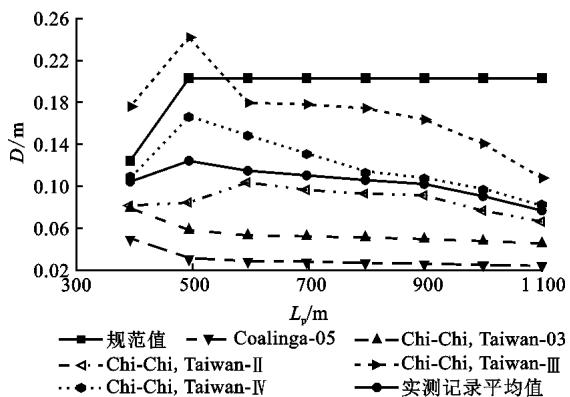
(a) I 类场地, T_g=0.25\text{s}
(b) II 类场地, T_g=0.45\text{s}
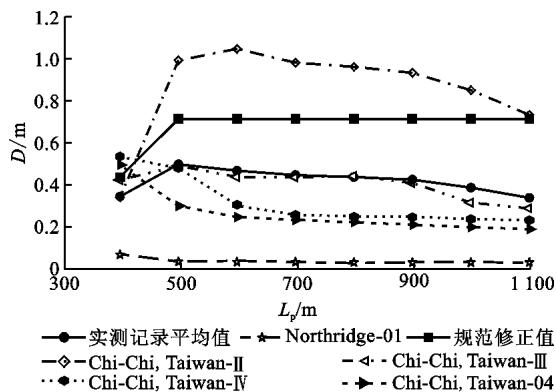
(c) Ⅲ类场地, T_g=0.65\text{s}
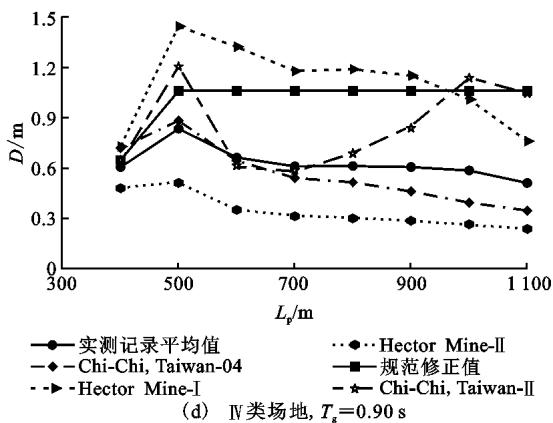
(d) IV 类场地, T_g=0.90\text{s}
图 9 实测记录对应位移谱与规范修正谱的比较
3.3 计算结果与结论
依据上述结构参数假定和地震动输入进行大量计算:① L_p 取 400\sim 1100\text{m},共 8 项;② 场地类型 I \sim IV 类共 4 项;③ 输入方式为规范谱与规范修正谱,共 2 项;④ P_{GA} 分别取 0.05g, 0.1g, 0.15g, 0.2g, 0.3g, 0.4g 共 6 项,合计 384 个工况。
首先给出在 P_{GA} = 0.1g 时,不同场地类型下,分别按规范谱与规范修正谱计算的梁端最大横向位移随主跨跨度变化曲线,如图 10 所示。由图 10 可见:①按规范谱计算的梁端最大位移随斜拉桥主跨跨度的增大而增大,按规范修正谱计算的结果在跨度达到 500\text{m} 以后不再增加并保持不变;② 相同跨径条件下,场地类型对梁端最大位移有显著影响,梁端最大横向位移随 T_g 的增大而增大。
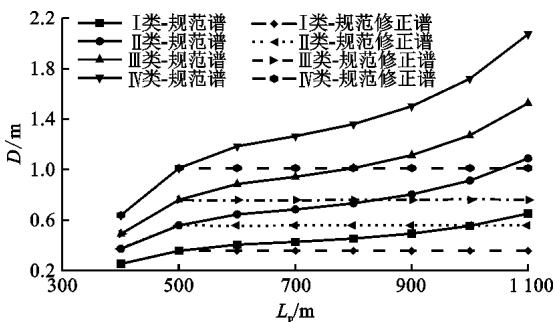
图 10 规范谱与规范修正谱梁端横向最大位移计算结果 (P_{GA}=0.1g)
当 P_{GA} 改变时,可直接乘以相应的比例系数。图 11 为 4 类场地类型输入下,分别按照规范谱和规范修正谱计算的梁端最大位移结果随 P_{GA} 的变化曲线。结合以往工程经验,如果以墩梁间最大横向位移 0.15\text{m} 作为斜拉桥边墩横向是否采用减震体系的标准,那么图 11 中直线以下即为可以不采用减震体系的使用范围,见表 5。
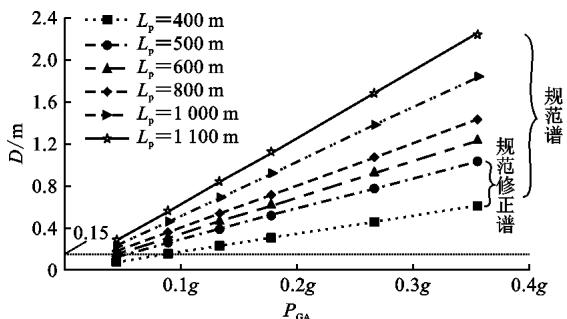
(a) I 类场地, T_g=0.25\text{s}
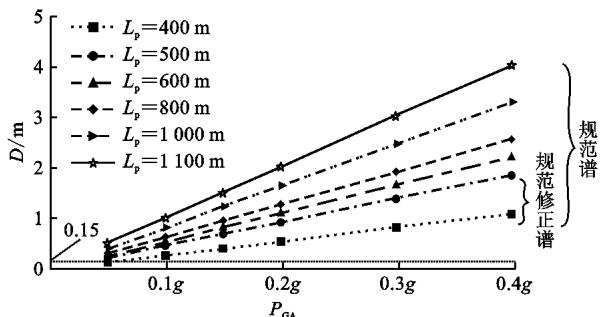
(b) II 类场地, T_g=0.45\text{s}
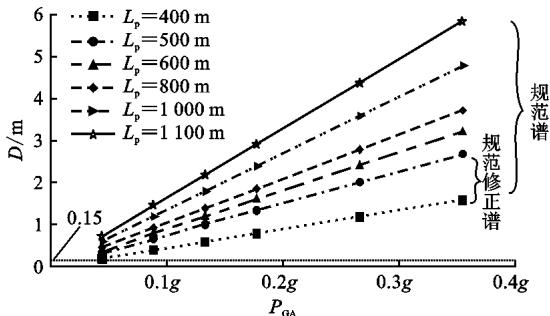
(c) Ⅲ类场地, T_g=0.65\text{s}
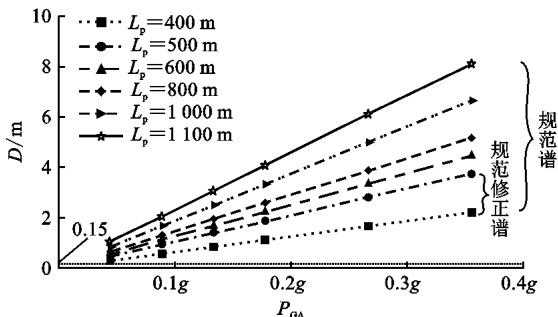
(d) IV 类场地, T_g=0.90\text{s}
图 11 不同 P_{GA} 下规范谱与规范修正谱计算结果
表 5 不同输入下无需考虑减震体系的使用范围
| 场地类型 | 规范谱 | 规范修正谱 |
|---|---|---|
| I类场地 | P_{GA} < 0.1g \cap L_p < 600\text{m} | P_{GA} < 0.1g \cap L_p < 600\text{m} |
| II类场地 | P_{GA} < 0.1g \cap L_p < 500\text{m} | P_{GA} < 0.1g \cap L_p < 500\text{m} |
| III, IV类场地 | 无 | 无 |
4 结语
(1)大跨度斜拉桥梁端横向位移以第 1 阶控制为主,本文推导的梁端横向位移的简化计算方法能较好估计梁端横向位移。
(2) 以墩梁间最大位移为 0.15\text{m} 作为斜拉桥边墩横向采用减震体系的标准, Ⅲ、Ⅳ 类场地, 跨径大于 400\text{m} 斜拉桥均需考虑减震体系。
(3)对低烈度区桥梁:如结构的抗震能力大于地震需求,则建议采用全限位体系;而如果结构的抗震能力接近或小于地震需求,且墩梁间位移小于 0.15\text{m} 时,则建议采用全滑动体系。
(4)由于资料有限,对斜拉桥结构参数简化与假定有一定不妥之处,涉及简化公式也有进一步精简与完善之处,这将是后续工作的重点。
参考文献
杨喜文, 张文华, 李建中. 大跨度斜拉桥横桥向减震研究 [J]. 地震工程与工程振动, 2012, 32(1): 86-92. \text{YANG Xi-wen, ZHANG Wen-hua, LI Jian-zhong}. \text{Seismic Design for Long-span Cable-stayed Bridges in Transverse Direction}[J]. \text{Earthquake Engineering and Engineering Vibration}, 2012, 32(1):86\text{-}92. ↩
徐略勤, 李建中. 挡块对斜拉桥横向抗震体系的影响 [J]. 振动与冲击, 2011, 30(11):57-61. \text{XU Lue-qin, LI Jian-zhong}. \text{Influence of Side Retainers on Transverse Anti-seismic System in Cable-stayed Bridge}[J]. \text{Journal of Vibration and Shock}, 2011, 30(11):57\text{-}61. ↩
叶爱君, 范立础. 超大跨度斜拉桥的横向约束体系 [J]. 中国公路学报, 2007, 20(2): 63-67. \text{YE Ai-jun, FAN Li-chu}. \text{Lateral Constraint Systems for Super-long-span Cable-stayed Bridge} [J]. \text{China Journal of Highway and Transport}, 2007, 20(2): 63\text{-}67. ↩
徐秀丽, 刘伟庆, 李龙安, 等. 斜拉桥结构减震设计优化研究 [J]. 地震工程与工程振动, 2006, 26(2): 119-124. \text{XU Xiu-li, LIU Wei-qing, LI Long-an, et al}. \text{Optimized Earthquake Reduction Design of Cable-stayed Bridges} [J]. \text{Earthquake Engineering and Engineering Vibration}, 2006, 26(2):119\text{-}124. ↩
冯云成, 燕斌, 牟宗军. 弹性索和阻尼器对斜拉桥横向抗震性能的影响 [J]. 工程抗震与加固改造, 2009, 31(4):24-28. \text{FENG Yun-cheng, YAN Bin, MOU Zong-jun}. \text{Effects of Elastic Cables and Dampers on Lateral Seismic of Cable-stayed Bridge}[J]. \text{Earthquake Resistant Engineering and Retrofitting}, 2009, 31(4):24\text{-}28. ↩
刘伟庆, 徐秀丽, 吴晓兰, 等. 大跨度斜拉桥结构横向消能减震设计方法 [J]. 振动工程学报, 2006, 19(3): 426-432. \text{LIU Wei-qing, XU Xiu-li, WU Xiao-lan, et al}. \text{Design Method of Energy-dissipated Earthquake-reduction along Transverse of Long-span Cable-stayed Bridges} [J]. \text{Journal of Vibration Engineering}, 2006, 19(3): 426\text{-}432. ↩
沈星, 倪晓博, 叶爱君. 大跨度斜拉桥边墩新型横向钢阻尼器减震体系及设计方法 [J]. 土木工程学报, 2016, 49(5): 110-119. \text{SHEN Xing, NI Xiao-bo, YE Ai-jun}. \text{Seismic System and Design Method of Transverse Metallic Yielding Dampers on Long-span Cable-stayed Bridge Side Piers} [J]. \text{China Civil Engineering Journal}, 2016, 49 (5): 110\text{-}119. ↩ ↩
\text{SHEN X, CAMARA A, YE A J}. \text{Effects of Seismic Devices on Transverse Responses of Piers in the Sutong Bridge} [J]. \text{Earthquake Engineering and Engineering Vibration}, 2015, 14(4):611\text{-}623. ↩
沈星, 倪晓博, 叶爱君. 桥梁新型横向金属阻尼器研究 [J]. 振动与冲击, 2014, 33(21):96-101. \text{SHEN Xing, NI Xiao-bo, YE Ai-jun}. \text{A New Type of Metallic Damper for Bridges' Aseismic Performance in Transverse Direction} [J]. \text{Journal of Vibration and Shock}, 2014, 33(21):96\text{-}101. ↩ ↩
\text{JTG/T B}02\text{-}01\text{—}2008, \text{公路桥梁抗震设计细则}[S]. \text{JTG/T B}02\text{-}01\text{—}2008, \text{Guidelines for Seismic Design of Highway Bridges}[S]. ↩
\text{CAMARA A}. \text{Seismic Behavior of Cable-stayed Bridges: Design, Analysis and Seismic Devices}[D]. \text{Madrid}: \text{Technical University of Madrid}, 2011. ↩
\text{WYATT T A}. \text{The Dynamic Behaviour of Cable-stayed Bridges: Fundamentals and Parametric Studies} [C]// \text{ITO M}. \text{Cable-stayed Bridges: Recent Developments and Their Future}. \text{New York}: \text{Elsevier Science Publishers}, 1991: 151\text{-}170. ↩
\text{JTG/T D}65\text{-}01\text{—}2007, \text{公路斜拉桥设计细则}[S]. \text{JTG/T D}65\text{-}01\text{—}2007, \text{Guidelines for Design of Highway Cable-stayed Bridge}[S]. ↩
\text{CAMARA A, ASTIZ M A, YE A}. \text{Fundamental Mode Estimation for Modern Cable-stayed Bridges Considering the Tower Flexibility}[J]. \text{Journal of Bridge Engineering}, 2014, 6(2): 13\text{-}21. ↩
李闯, 倪晓博, 叶爱君. 不同规范反应谱对桥梁减隔震设计的影响 [J]. 结构工程师, 2013, 29(5):91-95. \text{LI Chuang, NI Xiao-bo, YE Ai-jun}. \text{Influence of Different Response Spectrum in Codes on Isolated Bridge Design}[J]. \text{Structural Engineers}, 2013, 29(5):91\text{-}95. ↩