叶爱君, 苏振宇
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要:在以往的斜拉桥地震反应分析中,大都采用单桁架 (SECS) 模型来模拟斜拉索,不能反映斜拉索的局部振动的影响。以世界第一跨度斜拉桥——苏通大桥为背景,采用多桁架 (MECS) 模型来分析斜拉索局部振动对超大跨度斜拉桥地震反应的影响,并探讨了斜拉索的合理单元划分方式。结果表明,斜拉索划分为 10 个单元已能够很好地反映斜拉索局部振动的影响。考虑斜拉索局部振动之后,会出现索梁耦合振型,减小一些振型的参与系数,基频与主梁的竖向振动相近的斜拉索在地震作用下大幅振动,而主梁和主塔的内力反应普遍减小,特别是主塔的地震轴力明显减小。
关键词:斜拉桥;斜拉索局部振动;地震反应;内共振
中图分类号:U442.55
文献标识码:A
Effect of Cable Vibration on Seismic Response of Super-Long Span Cable-Stayed Bridge
YE Aijun, SU Zhengyu
(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: Single element cable system (SECS) model is usually adopted in the seismic response analysis of cable-stayed bridges, but the local vibration of cables cannot be simulated. A case study was made of the longest span cable-stayed bridge in the world, the Sutong Bridge, to investigate the effect of cable vibration on seismic response. Its analytical model was established, in which cables were modeled with multiple element cable system (MECS), and rational discretization manner was discussed. The results show that rational discretization manner divides each cable into 10 elements. Cable vibration changes the dynamics characteristics of the whole bridge; especially, cable-deck coupled modes may appear by reducing the participation factors of some modes. The seismic forces of girder and tower decrease, especially the axial force of the tower. Furthermore, internal resonance makes the cables whose frequencies are close to vertical vibration frequency of the girder vibrate seriously.
Key words: cable-stayed bridge; local vibration of cables; seismic response; internal resonance
众所周知,斜拉索是斜拉桥的重要承重结构,目前关于斜拉索的研究很多。但在桥梁抗震研究中,由于斜拉索的地震反应不控制设计,故往往更关心主体结构的地震反应1,如主梁和主塔的地震反应。对于斜拉索,通常采用单根桁架单元来模拟,这一方法简单实用,但是却不能反映斜拉索局部振动对桥梁地震反应的影响。事实上,斜拉索的局部振动会影响斜拉桥的动力特性,甚至会出现索梁耦合共振等复杂的非线性动力学现象2。当今斜拉桥的跨度越来越大,特别是苏通大桥已经突破千米级,在如此大的跨度下,研究斜拉索的局部振动对斜拉桥的地震反应的影响是十分必要的。
目前,国内外在这方面的研究主要体现在以下几方面。Caetano 等做了振动台试验并结合有限元模拟分析,提出在斜拉索局部振动不是很强时,地震反应减小,但在窄带地震作用下,地震反应会增大。Abdel-Ghaffar4研究了斜拉索局部振动对斜拉桥动力特性的影响,得出斜拉索的局部振动对某些振型的参与系数有影响,在计算地震反应时应该考虑索的局部振动的结论。国内学者布占宇等通过分析杭州湾大桥的地震反应,认为考虑斜拉索的局部振动后,地震反应会增大。王波等研究了地震卓越频率、主梁竖向振动频率和斜拉索的基频之间的匹配关系对斜拉桥地震反应的影响。
Caetano 等所做的试验和有限元模型计算都是基于缩尺模型的,并且采用的是只包含主梁竖向振动和斜拉索基频的人工波(意在激起斜拉索的剧烈振动),有两点作者认为值得探讨:①地震动时程不可能是一个只包含主梁竖向振动和斜拉索基频的窄带过程,特别是像苏通大桥这样大跨度的桥梁,主梁竖向振动频率和斜拉索基频都是很小,地震波的能量不可能全部集中在这一区域。用窄带人工波激励得到的结果是否有实际意义值得探讨;②已有的研究主要集中于对中小跨径斜拉桥的研究,超大跨径斜拉桥斜拉索局部振动影响是否和已有的研究结果相一致值得研究。
本文以苏通大桥为工程背景,采用有限元程序 SAP2000,分析了斜拉索局部振动对斜拉桥动力特性的影响,并探讨了斜拉索单元划分的合理方式。再基于桥址场地的地震动加速度时程,采用时程分析方法分析了斜拉索局部振动对斜拉桥地震反应的影响,结果表明斜拉索局部振动使斜拉桥的总体反应变小。
1 动力分析模型
本文以苏通大桥为背景建立了超大跨度斜拉桥的动力计算模型,并进行分析研究。苏通大桥为 7 跨钢箱梁斜拉桥,主跨 1088\mathrm{m} ,主桥通航孔布置为 100\mathrm{m} + 100\mathrm{m} + 300\mathrm{m} + 1088\mathrm{m} + 300\mathrm{m} + 100\mathrm{m} + 100\mathrm{m} 。全桥共 272 根斜拉索。
桥梁动力计算有限元模型如图 1 所示,斜拉索编号从左到右依次为 1 到 68 号(左半跨)。主塔、辅助墩和锚固墩处的桩基础并桩处理,并合理模拟了桩基的刚度特性,其他边界条件见表 1。
在计算模型中,考虑了恒载的几何刚度影响,同时利用 Ernst 公式考虑了斜拉索的垂度效应。
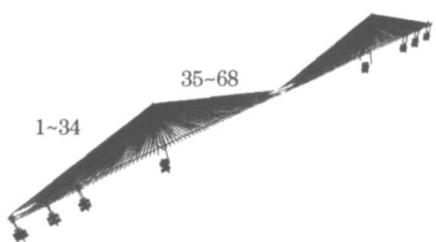
图 1 全桥有限元模型图
Fig.1 Finite element model of Sutong bridge
表 1 边界与连接条件
Tab.1 Boundary condition
| 位置 | 自由度 | |||||
| x | y | z | θx | θy | θz | |
| 主塔与主梁之间 | 0 | 1 | 0 | 0 | 0 | 0 |
| 锚固、辅助墩与主梁之间 | 0 | 1 | 1 | 0 | 0 | 0 |
注:“x”为纵桥向,“y”为横桥向,“z”为竖桥向。
2 动力特性分析
2.1 斜拉索动力特性与主桥动力特性的比较
本文首先计算斜拉索的动力特性,图 2 显示了 68 根斜拉索的前 6 阶振型周期,桥梁的动力特性如图 3 所示。
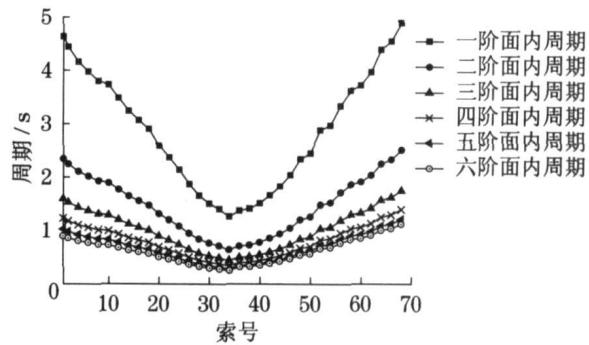
图 2 斜拉索前 6 阶振型周期
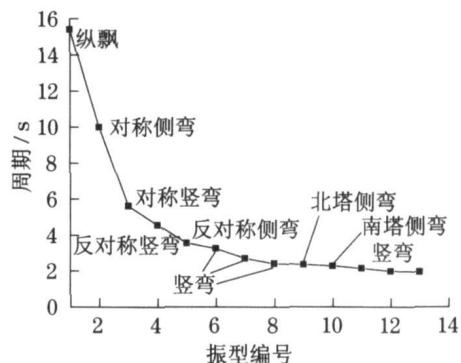
Fig.2 The first six modals of cables
图 3 主桥前 13 阶周期
Fig.3 The first thirteen modals of bridge
比较图 2,图 3 可知,斜拉索基频和主梁竖弯频率有一定重合,如主梁的一阶反对称竖弯频率与 62,63 号索的基频,二阶反对称竖弯频率与 49,50,51 号索的基频,三阶对称竖弯频率与 23,24,25,26 号索的基频很接近,很有可能发生索梁共振,可以预见这些索都会产生大幅振动,图 4 显示了三个典型的索梁共振振型。
2.2 斜拉索局部振动对斜拉桥动力特性的影响
每根斜拉索划分为 10 个单元,采用多桁架 (Multiple Element Cable System, MECS) 模型模拟,计算了全桥的动力特性,并特别比较了不考虑斜拉索局部振动单桁架 (Single Element Cable System, SECS) 模型和考虑斜拉索局部振动 MECS 模型时桥的动力特性(见表 2),发现两者有着一定的区别。
从表 2 中可看出考虑斜拉索局部振动之后会出现很多额外的振型,使得以主梁和主塔振动为主振型的出现推迟。全部振型可分为三种类型(见图 5):①只包含梁塔振动的振型(图 5a);②只包含斜拉索振动的振型(图 5b);③包含索梁耦合共振的振型(图 5c)。

a 一阶反对称竖弯 (T = 4.67\mathrm{s})
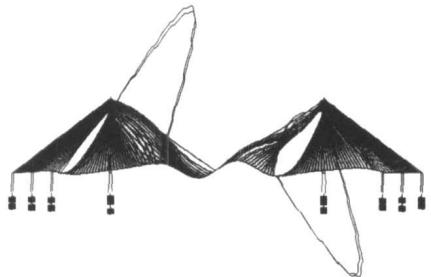
b 二阶反对称竖弯 (T = 2.68\mathrm{s})
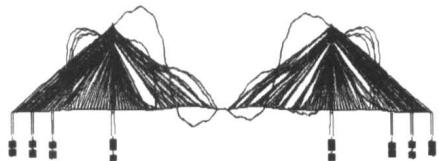
c 三阶对称竖弯 (T = 2.41\mathrm{s})
表 2 SECS 模型和 MECS 模型桥梁动力特性比较
Tab.2 Comparison of dynamics characteristics of SECS model and MECS model
| 振型号 | SECS 模型 周期/s | 振型号 | MECS 模型 周期/s | 振型特征 |
| 1 | 15.406 2 | 1 | 15.409 8 | 纵飘 |
| 2 | 9.995 8 | 2 | 9.894 0 | 对称侧弯 |
| 3 | 5.626 5 | 3 | 5.655 7 | 对称竖弯 |
| 4 | 4.561 9 | 20 | 4.673 6 | 反对称竖弯 |
| 5 | 3.569 9 | 130 | 3.493 2 | 反对称侧弯 |
| 6 | 3.257 1 | 149 | 3.168 3 | 竖弯 |
| 7 | 2.707 8 | 173 | 2.683 6 | 竖弯 |
| 8 | 2.420 8 | 189 | 2.410 9 | 竖弯 |
| 9 | 2.356 5 | 194 | 2.333 1 | 北塔侧弯 |
| 10 | 2.279 4 | 199 | 2.250 2 | 南塔侧弯 |
| 11 | 2.148 8 | 207 | 2.101 1 | 竖弯 |
2.3 斜拉索局部振动对振型参与系数的影响
为了进一步分析斜拉索局部振动对地震反应的影响,本文对两种模型的振型参与系数进行了比较(见图 6)。以不考虑斜拉索局部振动模型为准选取前 15 阶振型,考虑斜拉索振动的模型取相应振型。
从图 6 中可以看出,在考虑斜拉索局部振动之后,三个方向的振型参与系数都有一定改变,并且由于出现了大量新的振型,而这些振型也有着一定的参与系数,造成了多桁架模型的振型参与系数普遍比单桁架模型小,从而引起地震反应的变化。
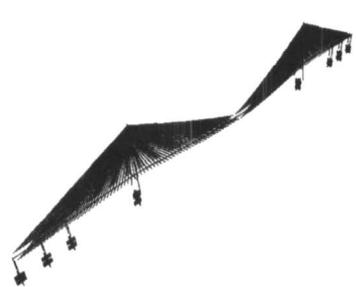
Fig.4 Cables and deck internal resonance modals
a 只包含梁塔振动的振型
图 5 考虑斜拉索局部振动后的三种振型图
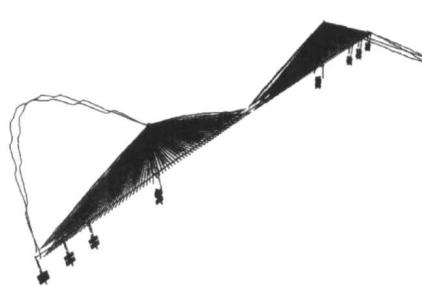
图 4 索梁共振振型图
b 只包含斜拉索振动的振型
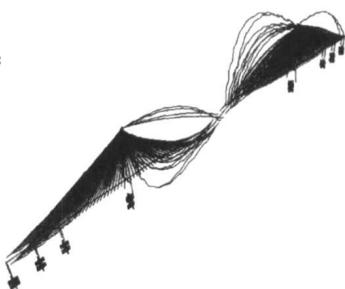
c 包含索梁耦合共振的振型
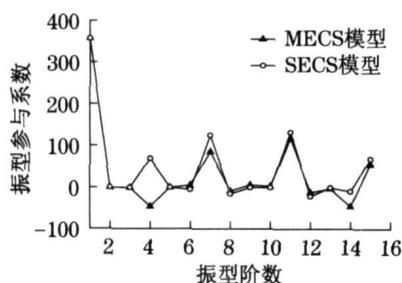
a x 方向
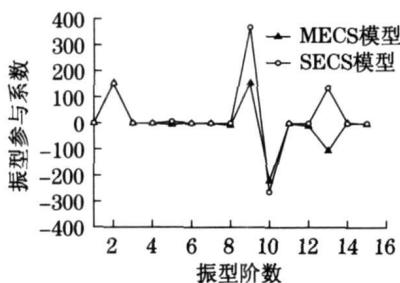
Fig.5 Modals of MECS model
b y 方向
图 6 三个方向的振型参与系数比较图
Fig.6 Modal participation factors comparison
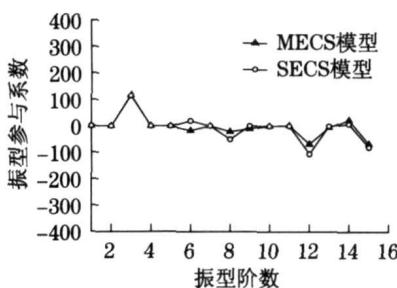
c z 方向
3 地震反应时程分析
3.1 地震动输入
本文采用苏通大桥场地安评报告所给的 2500 年重现期的 10 条地震加速度时程作为输入进行地震反应分析。第 1 条地震加速度时程如图 7 所示,把所给 10 条加速度时程转换为反应谱如图 8 所示。
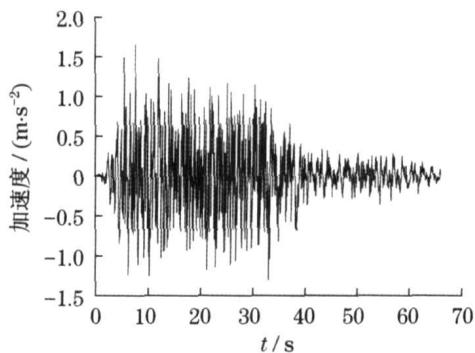
图 7 1 号加速度时程
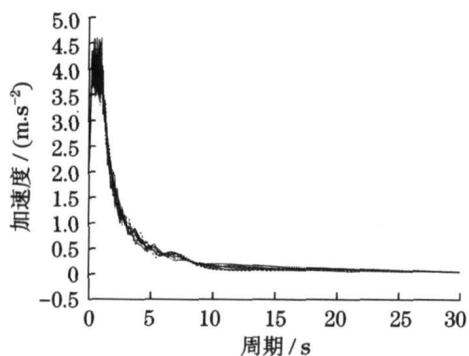
Fig.7 The first earthquake acceleration time history
图 8 10 条地震加速度时程对应的反应谱
Fig.8 Response spectra corresponding to ten earthquake acceleration on time histories
3.2 斜拉索单元划分的合理方式
在分析斜拉索局部振动影响时,斜拉索单元划分的合理方式,即每根斜拉索的合理单元数是一个必须解决的问题,单元划分太多则计算困难,太少则不能真实反映局部振动的影响。
本文分析表明,斜拉索划分单元数超过 20 以后,桥梁地震反应变化非常小,因此本文以 20 作为基准,分别将斜拉索划分为 3,5,8,10 个单元,分析了主梁的轴力、剪力、弯矩与 20 个单元对应反应的误差,如图 9 所示。
从图 9 中可以看出当斜拉索仅仅用 1 个单元模拟时误差较大,弯矩最大误差超过 25\% ,即不考虑斜拉索局部振动比考虑斜拉索振动后大了约 25\% 。轴力最大误差为 5\% 左右,当斜拉索划分为 10 个单元后,误差已经相当小。故本文选择将一根斜拉索离散为 10 个单元。
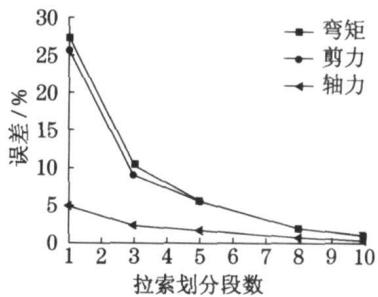
图 9 斜拉索划分段数的影响
Fig.9 Effect of cable discrete on girder seismic response
3.3 主梁的地震反应
一般斜拉桥主梁的地震反应不控制设计,但为了全面地分析斜拉索局部振动对桥梁的地震反应的影响,本文着重考察了斜拉索局部振动对主梁的四个代表性截面(见图 10)地震反应的影响。图 10 中 G1,G2,G3,G4 分别为第一边跨跨中、第二边跨跨中、主塔下、主梁跨中截面。图 11 显示了 10 条地震加速度时程分别沿纵向 + 竖向、横向 + 竖向输入时斜拉索局部振动对主梁四个代表截面的轴力弯矩影响,表 3 则列出了 10 条地震加速度时程输入时影响的平均值。
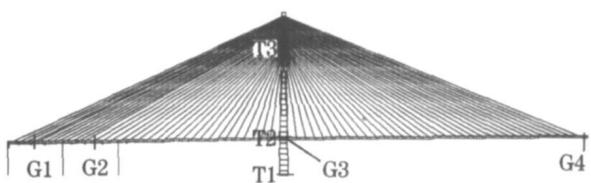
图 10 主梁和主塔关键截面
Fig.10 Key sections of tower and girder
表 3 主梁影响量平均值
Tab.3 Average cable vibration effect on girder %
| 截面 | 纵向+竖向 | 横向+竖向 | ||
| 轴力 | 弯矩 | 轴力 | 弯矩 | |
| G1 | -2.0 | -9.0 | 1.6 | -5.4 |
| G2 | -1.8 | -5.2 | 1.0 | -7.3 |
| G3 | -1.3 | -3.2 | -0.6 | -1.1 |
| G4 | 0.5 | -4.1 | -6.3 | -2.9 |
从图 11 可以发现考虑斜拉索局部振动后,在纵向 + 竖向输入时,主梁轴力和弯矩基本上都是减小的,轴力减小幅度比较小,而弯矩减小幅度较大,最大可到 15\% 。在横向 + 竖向输入时,主梁的地震轴力变化规律性不强,主梁弯矩基本都减小,最大幅值达到 12\% 左右。表 3 的数据表明,斜拉索局部振动导致主梁的地震反应普遍减小,最大平均减小了 9\%。
a 纵向 + 竖向输入
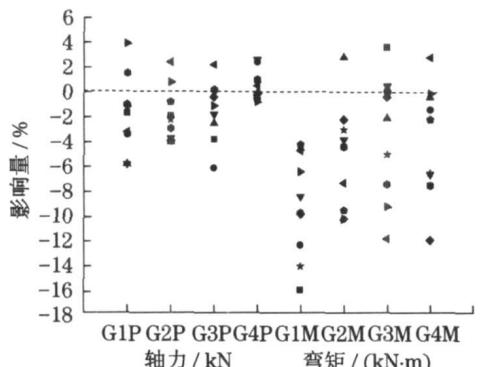
\mathrm{G1P}\sim \mathrm{G3P} 分别为 \mathrm{G1}\sim \mathrm{G3} 截面轴力; \mathrm{G1M}\sim \mathrm{G3M} 分别为 \mathrm{G1}\sim \mathrm{G3} 截面弯矩.
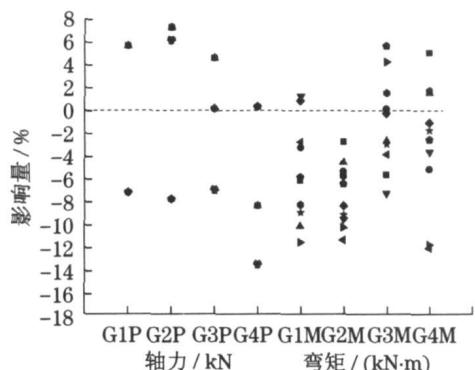
b 横向 + 竖向输入
图 11 斜拉索局部振动对梁内力影响
3.4 主塔的地震反应
塔是斜拉桥的主要受力构件,地震力往往控制其设计,本文着重考察了斜拉索局部振动对主塔的三个关键截面(见图 10)地震反应的影响。图 10 中 T1,T2,T3 分别为塔底、下横梁上侧、以及主塔交叉点下侧截面。图 12 显示了 10 条地震加速度时程分别沿纵向 + 竖向、横向 + 竖向输入时斜拉索局部振动对主塔三个关键截面的轴力弯矩影响,表 4 则列出了 10 条地震加速度时程输入时影响的平均值。
Fig.11 Effect of cable vibration on girder seismic force
a 纵向 + 竖向输入
图 12 斜拉索局部振动对塔关键截面内力影响
Fig.12 Effect of cable vibration on tower seismic force
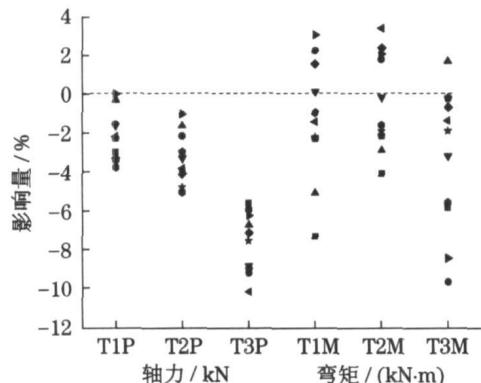
T1P \sim T3P 分别为 T1~T3 截面轴力; T1M \sim T3M 分别为 T1~T3 截面弯矩.
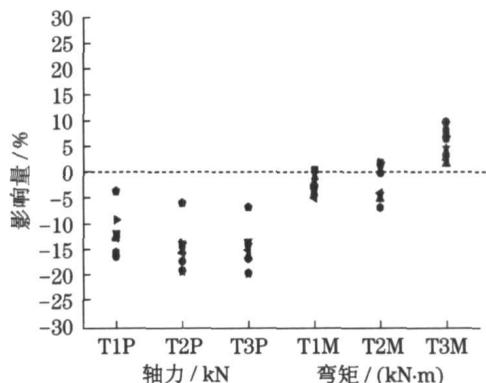
b 横向 + 竖向输入
表 4 主塔影响量平均值
Tab.4 Average cable vibration effect on tower %
| 截面 | 纵向+竖向 | 横向+竖向 | ||
| 轴力 | 弯矩 | 轴力 | 弯矩 | |
| T1 | -2.1 | -1.2 | -13.3 | -2.2 |
| T2 | -3.3 | -0.3 | -16.1 | -2.4 |
| T3 | -7.7 | -3.5 | -16.1 | 5.1 |
从图 12 可以看出,在纵向 + 竖向地震激励下,斜拉索局部振动对于主塔的关键截面的影响较小,主塔轴力全部减小,减小最大超过 10\% ;弯矩也普遍减小,最多减小 9\% 。在横向 + 竖向地震激励下,主塔关键截面的轴力减小较大,最大减小 28\% 左右,T1,T2 弯矩变化很小,T3 截面弯矩稍有增加。这主要是因为横桥向主塔结构呈倒 Y 型,在交叉点以下弯矩的变化转化成了“两条腿”轴力的变化。
表 4 的数据表明,斜拉索局部振动导致主塔的地震反应普遍减小,最大平均减小了 16\%。
3.5 节点位移的地震反应
为了全面地反映斜拉索局部振动对斜拉桥地震反应的影响,本文还考察了斜拉索局部振动对斜拉桥地震位移的影响,重点考察了塔顶、梁端以及跨中的位移变化情况,表 5 列出了 10 条地震加速度时程输入时对位移影响的平均值。
表 5 斜拉索局部振动对关键节点位移的平均影响量
Tab.5 Average cable vibration effect on displacement of key points
| 位置 | 纵向+竖向输入 | 横向+竖向输入 | ||
| 纵向 | 竖向 | 横向 | 竖向 | |
| 塔顶 | -1.43 | 0.00 | -15.50 | 0.00 |
| 梁端 | -0.04 | 0.00 | -1.59 | 0.00 |
| 跨中 | -0.15 | -0.56 | 0.45 | -0.23 |
从表 5 看出,在纵向 + 竖向输入下,斜拉索局部振动对斜拉桥关键节点的位移影响很小;而在横向 + 竖向输入下,斜拉索局部振动使塔顶横向位移明显减小,平均减小 15.5\% ,对其他节点位移影响很小。
3.6 斜拉索的地震反应
由于斜拉索的脉动张拉力并不控制设计,故本文没有列出斜拉索局部振动对地震拉力的影响。但着重考虑了各斜拉索中点在 1 号地震动时程纵向输入时的纵向位移,如图 13 所示。可以看出,在给定地震激励下,23,24,25,26 号索和 49,50,51 号索以及 62,63 号索振动很大,这是由于这些斜拉索的基频刚好处于主梁低阶竖向振动频率附近,以至于产生了索梁的内共振现象,从前面的动力特性分析中可以清楚地看到这一点。
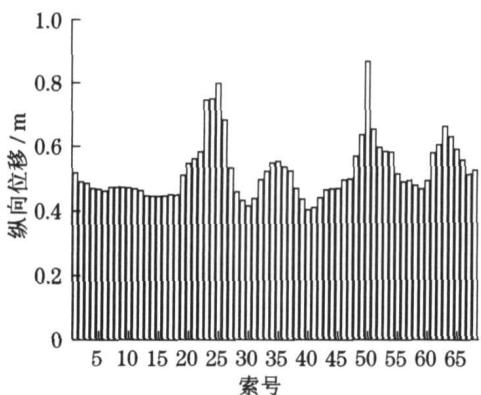
图 13 拉索中点的纵向位移
Fig.13 Longitudinal displacement of middle point of cable
4 结论
本文以苏通大桥为背景,采用 10 条桥梁场地地震加速度时程,分析了斜拉索局部振动对超大跨径斜拉桥地震反应的影响,得到以下结论:
(1) 考虑斜拉索局部振动后,斜拉桥的动力特性产生较大变化,出现纯索的振型和索梁耦合振型。
(2) 考虑斜拉索局部振动后,各个振型都参与贡献,使得各个振型的参与系数普遍有所减小,并引起斜拉桥的地震反应产生变化。
(3) 单根斜拉索划分为 10 个单元来考虑斜拉索局部振动、计算地震反应已经有足够的精度。
(4) 考虑斜拉索局部振动后,斜拉桥的地震反应普遍减小。主梁弯矩的最大平均减小量为 9\% ,横向输入时主塔轴力最大平均减小量为 16\% ,塔顶位移最大平均减小量为 15.5\% ,其他反应分量影响不大。
(5) 在地震作用下,由于索梁的内共振,基频与主梁的竖向振动频率相近的斜拉索会产生大幅振动。
参考文献:
叶爱君·桥梁抗震 [M]. 北京:人民交通出版社,2002. YE Ajun. Seismic design of bridge [M]. Beijing: China Communications Press, 2002. ↩
Caetano E, Cunha A, Gattulli V, et al. Cabledeck dynamic interactions at the International Guadian Bridge: On site measurements and finite element modeling[J]. Structure Control and Health Monitoring, 2008, 15:237. ↩
Caetano E, Cunha A, Taylor C A. Investigation of dynamic cabledeck interaction in a physical model of a cable-stayed bridge, Part I: Modal analysis [J]. Earthquake Engineering and Structure Dynamics, 2000, 29:481.
Abdel-Ghaffar A M. Importance of cable vibration and dynamics of cable stayed bridges [J]. Journal of Engineering Mechanics, 1991, 117(1):2571. ↩
布占宇, 谢旭, 苟昌焕. 拉索局部振动对斜拉桥地震反应的影响研究 [J]. 工程力学, 2006, 23(9): 157. BU Zhanyu, XIE Xu, GOU Changhuan. Effect of local cable vibration on the seismic response of cable stayed bridges[J]. Engineering Mechanics, 2006, 23(9): 157.
王波, 张海, 徐丰. 考虑拉索局部振动的斜拉桥地震响应分析 [J]. 西南交通大学学报, 2008, 43(4): 441. WANG Bo, ZHANG Hai, XU Feng. Seismic time history response analysis of cable stayed bridge with local cable vibration [J]. Journal of Southwest Jiaotong University, 2008, 43(4):441.
Caetano E, Cunha A, Taylor C A. Investigation of dynamic cabledeck interaction in a physical model of a cable-stayed bridge. Part - II: Seismic response[J]. Earthquake Engineering and Structure Dynamics, 2000, 29:499.