刘伟岸 叶爱君 王斌斌
(同济大学桥梁工程系,上海 200092)
摘要 以苏通大桥为例,通过分析比较工程上常用的 6 弹簧模型、等效嵌固模型、集中质量模型以及弹性嵌固模型,得出各模型的优缺点,并发现弹性嵌固模型能较好地模拟桩土相互作用下桩基地震动反应。
关键词 桩基,大跨度桥梁,桩土相互作用,弹性嵌固模型,阻抗矩阵
Discussion on Seismic Simplified Modes of Pile Foundation in Long-Span Bridges
LIU Weian, YE Aijun, WANG Binbin
(Department of Bridge Engineering, Tongji University, Shanghai 200092, China)
Abstract In the seismic analysis of pile foundation, the soil-pile-structure interaction has been always a complicated issue. Taking Sutong bridge as an example, the common seismic models like 6-spring model, equivalent fixed model, lumped-mass model and elastic fixed model have been analyzed and compared in this paper. And it has been concluded that elastic fixed model can better simulate seismic responses of the pile foundation under the soil-pile-structure interaction.
Keywords pile foundation, long-span bridge, soil-pile-structure interaction, elastic fixed model, impedance matrix
1 前言
大跨度桥梁最常用的基础形式是群桩基础,而建于江海中的桥梁,广泛采用的是高桩承台基础。在桩基桥梁的地震反应分析中,业内已普遍认为应考虑群桩基础对桥梁地震反应的影响。但在桩基结构的地震反应分析中,桩 - 土 - 结构的相互作用问题一直是个难点。在大跨度桥梁的地震反应分析中,群桩基础的模拟方法主要有 3 种,从复杂到简化排序:① 集中质量法(集中质量模型);② 在冲刷线以下一定深度固结(等效嵌固模型);③ 用 6 根弹簧模拟桩基础的作用(6 弹簧模型)。另外还有一种新型但不常用的弹性嵌固模型。文献1,2,3,4对各种实用的桩基计算模型进行了综述和研究。
本文旨在分析比较这些常用的模型,并且对它们各自的适用性以及优缺点进行评述。
2 群桩基础常用模型简介
2.1 集中质量法
集中质量法的主要原理是将桥梁上部结构多质点体系和桩 - 土体系的质点联合作为一个整体,来建立整体耦联的地震振动微分方程组进行求解。该模型假定桩侧土是 Winkler 连续介质,将桩 - 土体系的质量按一定厚度简化并集中为一系列质点,离散成一个理想化的参数系统,并用弹簧和阻尼器模拟土介质的动力性质,形成一个地下部分的多质点体系,在地震作用下把结构物 - 桩 - 地基土作为一个完整的体系来分析其动力反应。如图 1 所示,将各单桩按同样的方式集中为若干个质点,然后将两个水平方向的弹簧和阻尼器直接加在群桩中每一单桩的相应节点上,在每一土弹簧处输入对应土层的自由场地地震动加速度时程。这一方法的力学意义简单明了,可直接算出单桩内力,结果也应最为准确,但对于大规模的群桩基础,所需附加的弹簧和阻尼器数量庞大,模型相当复杂。
为了简化群桩模型,很自然的思路是将桩基础进行合并。文献6对并桩模式进行了大量的参数研究,将整个群桩结构浓缩为一根合成的桩,如图 1 所示。这种模式比较简单,所用单元和节点数很少,而且只与场地土划分层数有关,与群桩所含单桩数无关,因此,群桩桩数越多,其优越性越明显。
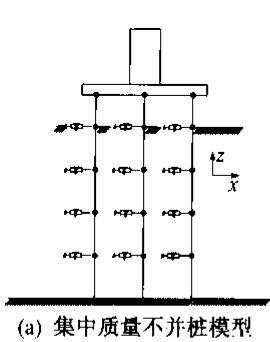
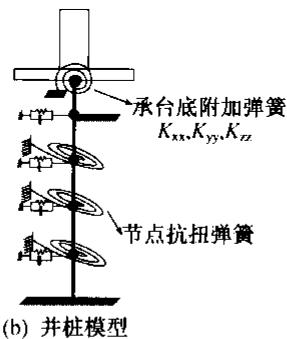
图 1 集中质量模型
2.2 在冲刷线以下一定深度固结
对于高桩承台,工程界常用的一种简化方法是将桩在冲刷线以下 3 \sim 5 倍直径处固结,来简化计算分析过程,如图 2 所示。一般认为,对于动力问题,桩在冲刷线以下的固结深度 H,实际上更为合理的是根据单桩水平刚度等效的原则来确定。文献7指出固结深度 H 的表达式为:
式中 K——整个桩基结构的抗推刚度;
I——桩的抗弯惯矩之和。
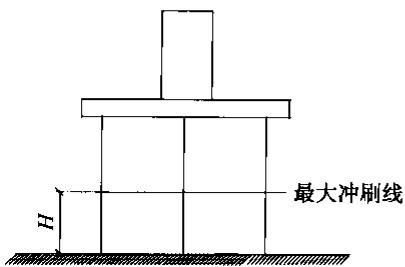
图 2 等效嵌固模型
但许多桩基础的计算分析表明,根据单桩水平刚度等效的原则确定的嵌固深度 H 仍然处于 3 \sim 5 倍直径范围内。
对于桩数很多的群桩基础,当然也可以采用图 1 所示的方法进行并桩处理。
2.3 用6根弹簧模拟桩基础的作用
在大跨度桥梁的地震反应分析中,桩基础的另一种常用处理方法是在承台底部加上 6 个方向的弹簧来模拟桩基础的作用(图 3),并由承台底部的内力按照静力方法反推单桩最不利受力。弹簧刚度根据土层状况和桩的布置形式按静力等效的原则确定,其中土性资料一般根据 m 法确定。这种处理方法非常简单,但实质上是用静力的方法来分析桩基的动力问题。特别是对于高桩承台,桩的自由长度部分实际是结构的一部分了,用 6 弹簧模型显得有些粗糙。
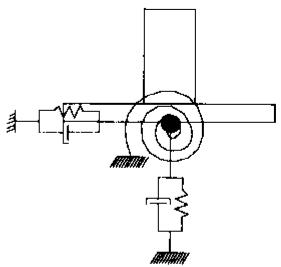
图 3 6 弹簧模型
2.4 弹性嵌固模型
文献4中提到一种独立桩模型,它是用一个弹簧单元或阻抗矩阵来有效模拟一根单桩与土相互作用和桩身的刚度对冲刷线以上主体结构的影响,此模型称为弹性嵌固模型。弹性嵌固模型的原理实际上同等效嵌固模型很类似,都是利用刚度等效的原则来近似模拟桩基,所不同的是弹性嵌固模型是在每根桩下用弹簧单元来近似模拟冲刷线下桩土的相互作用,如图 4 所示。该模型假定也是桩侧土为 Winkler 连续介质,它在地面线或冲刷线处将桩身截断,并将地震作用下的桩土相互作用和桩身的刚度对地面线或冲刷线以上主体结构的影响用弹簧单元或阻抗矩阵来模拟,并在冲刷线处输入自由场地地震动加速度时程。该模型既能考虑地震作用下桩土相互作用的影响,又能大大缩减模型的复杂程度,只是在确定阻抗矩阵的参数上有一定的困难。在不考虑非线性的基础上,该阻抗矩阵一般形如下式所示:
其中,K_{uz}, K_{ux}, K_{uy}, K_{rz}, K_{rx}, K_{ry} 分别为冲刷线以下桩身在竖向、纵桥向、横桥向的平动和转动刚度;K_{xy} 为纵桥向平动和横桥向转动的耦合刚度;-K_{yx} 为横桥向平动和纵桥向转动的耦合刚度。在只考虑弹性的范围内,这些参数都可以由桩基的地质资料通过基规求得,并且对于一般的桩基来说,每根桩的地质资料应该类似,这样只要求出一根桩的阻抗矩阵便可,工作量也可以得到缩减。
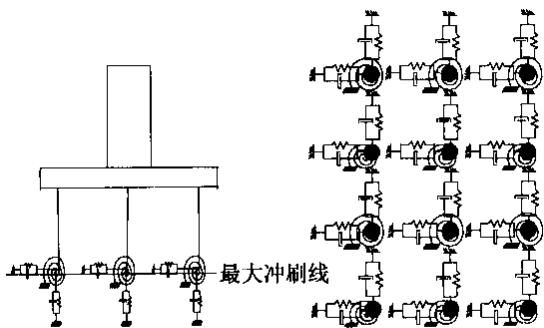
图 4 弹性嵌固模型:(a) 立面图 (b) 平面图
3 实例分析
3.1 实例一
本文先以苏通大桥的北近塔辅助墩为算例,用反应谱方法对这 4 种模型进行比较分析。
苏通大桥是建成后将成为世界第一的斜拉桥,其边墩包括近塔辅助墩、远塔辅助墩和过渡墩,墩身均采用分离的钢筋混凝土薄壁箱形空心墩,墩顶设纵向滑动、横向限位球型钢支座。其中,近塔辅助墩截面形式为 8.5\text{m} \times 5.0\text{m},壁厚 0.8\text{m},基础采用 36 根 \text{D}2.8\text{m}/\text{D}2.5\text{m} 变直径钻孔桩基础,承台平面尺寸为 52\text{m} \times 32.5\text{m}。
地震动输入采用规范四类场地反应谱作为地震输入,地震动峰值加速度为 0.1g,并且为纵桥向输入,阻尼比取为 5\%。
通过大型通用有限元软件 SAP2000 的计算,各模型计算结果如表 1~表 3 所示。由表 1、表 3 可以看出,不管是等效嵌固模型还是集中质量模型,利用简化的并桩计算模式与不并桩的模式分析结果基本相近,但并桩模式大大减少了计算量。因此,在今后的大跨度桥梁动力分析中利用并桩模式可以在只增加少量单元的条件下,进行上部结构和群桩基础一体的动力分析,很有价值。
表 1 前 5 阶振型频率比较
| 频率(\text{Hz}) | 6弹簧模型 | 等效嵌固模型 | 集中质量模型 | 弹性嵌固模型 |
|---|---|---|---|---|
| 并桩 | 不并桩 | 并桩 | ||
| x向一阶振动 | 0.633 | 0.571 | 0.580 | 0.571 |
| y向一阶振动 | 0.642 | 0.576 | 0.581 | 0.576 |
| y向二阶振动 | 1.104 | 1.094 | 1.097 | 1.094 |
| 桩基扭转 | - | - | 1.850 | - |
| x向二阶振动 | 3.727 | 3.601 | 4.201 | 3.585 |
注:X 向为纵桥向,Y 向为横桥向
表 2 桩质量为零时各模型振型频率
| 频率(\text{Hz}) | 6弹簧模型(考虑耦合) | 集中质量模型 |
|---|---|---|
| x向一阶振动 | 0.6088 | 0.6073 |
| y向一阶振动 | 0.6226 | 0.6182 |
| y向二阶振动 | 1.1073 | 1.1053 |
| x向二阶振动 | 3.5147 | 3.4209 |
表 3 各模型地震动反应比较
| 位置 | 地震反应 | 6弹簧模型 | 等效嵌固模型 | 集中质量模型 | 弹性嵌固模型 |
|---|---|---|---|---|---|
| 并桩 | 不并桩 | 并桩 | |||
| 墩顶 | 位移(\text{m}) | 0.127 | 0.139 | 0.135 | 0.139 |
| 墩底 | 剪力(\text{kN}) | 6.21\text{E}+03 | 6.16\text{E}+03 | 6.02\text{E}+03 | 6.17\text{E}+03 |
| 弯矩(\text{kN}\cdot\text{m}) | 2.26\text{E}+05 | 2.18\text{E}+05 | 2.13\text{E}+05 | 2.17\text{E}+05 | |
| 承台底 | 剪力(\text{kN}) | 4.57\text{E}+04 | 4.55\text{E}+04 | 4.58\text{E}+04 | 4.59\text{E}+04 |
| 弯矩(\text{kN}\cdot\text{m}) | 4.55\text{E}+05 | 4.43\text{E}+05 | 4.40\text{E}+05 | 4.44\text{E}+05 | |
| 桩顶 | 轴力(\text{kN}) | 4.71\text{E}+03 | 4.73\text{E}+03 | 4.76\text{E}+03 | 4.71\text{E}+03 |
| 剪力(\text{kN}) | 1.27\text{E}+03 | 1.30\text{E}+03 | 1.31\text{E}+03 | 1.31\text{E}+03 | |
| 弯矩(\text{kN}\cdot\text{m}) | 2.42\text{E}+04 | 2.68\text{E}+04 | 2.71\text{E}+04 | 2.65\text{E}+04 | |
| 冲刷线处 | 剪力(\text{kN}) | 1.27\text{E}+03 | 1.54\text{E}+03 | 1.56\text{E}+03 | 1.55\text{E}+03 |
| 弯矩(\text{kN}\cdot\text{m}) | 1.05\text{E}+04 | 1.23\text{E}+04 | 1.23\text{E}+04 | 1.26\text{E}+04 |
其次,表中结果表明,在基频上,以集中质量不并桩模型为基准,集中质量并桩模型、弹性嵌固模型、等效嵌固并桩模型的误差均非常小;等效嵌固不并桩模型由于单桩竖向刚度偏大,所以存在明显误差;误差最大的为 6 弹簧模型,由于忽略了承台以下桩身的质量和刚度矩阵中的非对角元素(即转动和平动刚度的耦合项)的影响,因此动力特性的误差较大。若使其他模型桩基的质量为零,并在 6 弹簧模型中给予考虑刚度矩阵的耦合项时,此时和 6 弹簧模型符合得较好,如表 2 所示。
在墩体结构和桩基结构的地震动反应上,如表 3 所示,以集中质量不并桩模型为基准,等效嵌固模型及其并桩模型桥墩的反应误差比较小,桩身的反应误差比较大;弹性嵌固模型的桥墩反应误差也稍大(最大达 8.8\%),但桩身的反应误差较小,均不超过 5.0\%;而 6 弹簧模型的地震反应误差较大,桥墩反应最大误差为 11.8\%,桩身反应的误差也较大,特别是冲刷线处,最大误差为 17\%。其中,6 弹簧模型是通过承台底的内力来反算最不利桩的内力,因此,是静力计算,没考虑桩身的地震惯性力,因此,结果偏小。
3.2 实例二
以主跨 1088\text{m},主梁全宽 40.6\text{m},高 4.0\text{m} 采用全封闭扁平流线形钢箱梁的苏通大桥全桥模型来分析以上几种模型,其 3 维有限元模型如图 5 所示。地震输入采用图 6 所示的水平加速度反应谱曲线,峰值加速度为 0.123g,进行纵向加竖向的地震动输入,并且阻尼比取为 5\%。
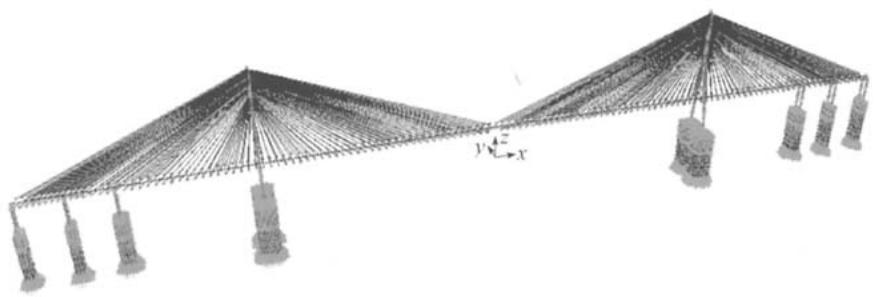
图 5 苏通大桥动力有限元模型
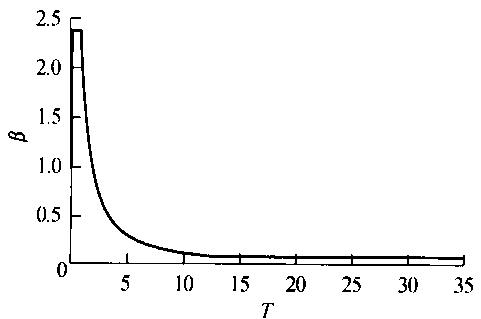
图 6 水平向加速度反应谱曲线
表 4 显示了 5 种模型,即集中质量模型、6 弹簧模型(已经考虑刚度矩阵耦合项)、弹性嵌固模型、等效嵌固模型及其并桩模型的前 5 阶振型频率。通过比较发现两者基本上是一致的,这主要是大跨度桥梁前几阶振型基本上是由上部结构控制的,另一方面也验证了它们的适用性。
表 4 前 5 阶振型频率
| 频率(\text{Hz}) | 集中质量模型 | 6弹簧模型 | 弹性嵌固模型 | 等效嵌固模型 |
|---|---|---|---|---|
| 不并桩 | ||||
| 纵飘 | 0.077 | 0.077 | 0.077 | 0.077 |
| 一阶对称侧弯 | 0.107 | 0.107 | 0.107 | 0.107 |
| 一阶对称竖弯 | 0.196 | 0.196 | 0.196 | 0.196 |
| 一阶反对称竖弯 | 0.241 | 0.241 | 0.241 | 0.242 |
| 万状弯侧弯 | 0.275 | 0.273 | 0.266 | 0.275 |
在 2 个主塔下群桩基础的地震反应上,通过表 5 可以看出,弹性嵌固模型表现出较好的适用性,与集中质量模型的误差比较小。相比而言,等效嵌固并桩以及不并桩模型误差则稍大,而 6 弹簧模型显得很粗糙,误差最大达到 16\%。在北塔下最不利桩的内力包络图上,弹性嵌固模型和等效嵌固模型跟集中质量模型符合得比较好,如图 7~图 9 所示。但是相比而言,弹性嵌固模型比等效嵌固模型能更好地反应桩基的地震动反应,其算得的结果精确度较高,误差较小。但是,弹性嵌固模型涉及到阻抗矩阵的计算,稍微有点烦杂,而等效嵌固模型则稍微简单,并可以通过并桩大大缩减体系自由度,提高计算效率。
表 5 主塔底群桩基础桩身最大内力比较
| 截面位置 | 分量 | 集中质量模型 | 6弹簧模型 | 弹性嵌固模型 | 等效嵌固模型 |
|---|---|---|---|---|---|
| 不并桩 | |||||
| 北塔塔底 | 轴力(\text{kN}) | 4.85\text{E}+03 | 4.04\text{E}+03 | 4.36\text{E}+03 | 4.68\text{E}+03 |
| 弯矩(\text{kN}\cdot\text{m}) | 2.15\text{E}+04 | 1.81\text{E}+04 | 2.17\text{E}+04 | 2.28\text{E}+04 | |
| 南塔塔底 | 轴力(\text{kN}) | 5.07\text{E}+03 | 4.56\text{E}+03 | 4.97\text{E}+03 | 5.00\text{E}+03 |
| 弯矩(\text{kN}\cdot\text{m}) | 2.13\text{E}+04 | 1.80\text{E}+04 | 2.14\text{E}+04 | 2.20\text{E}+04 |
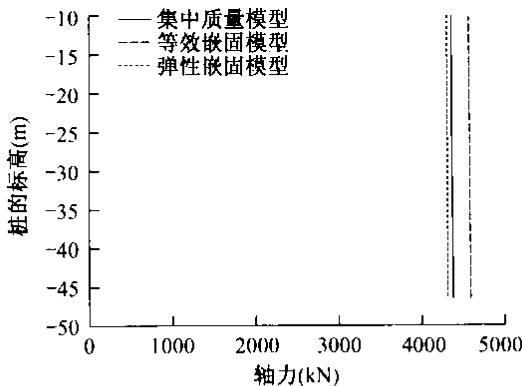
图 7 北塔下最不利桩轴力包络图
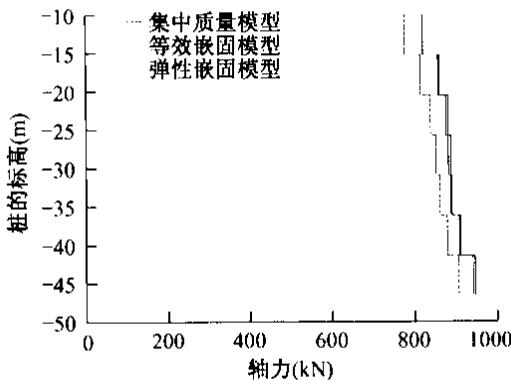
图 8 北塔下最不利桩剪力包络图
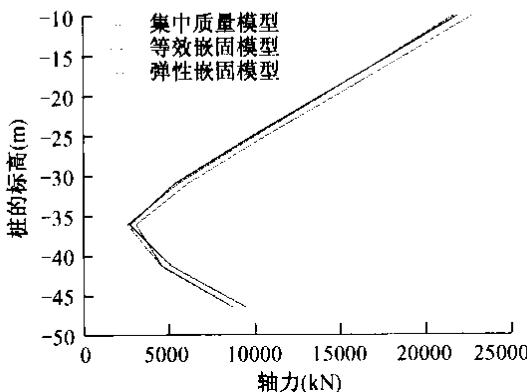
图 9 北塔下最不利桩弯矩包络图
4 结论
通过以苏通大桥的北近塔辅助墩模型和全桥模型为背景,对比大跨度桥梁的地震反应分析中群桩基础的几种模拟方法后得出结论如下:
(1)不管是等效嵌固模型还是集中质量模型,利用简化的并桩计算模式与不并桩的模式分析结果基本相近,但并桩模式可大大减少计算量。因此在今后的大跨度桥梁动力分析中利用并桩模式可以在只增加少量单元的条件下,进行上部结构和群桩基础一体的动力分析,这样可以大大缩减体系的自由度,很有价值。
(2)对于分析的等效嵌固模型、6 弹簧模型和弹性嵌固模型,在自振频率上跟上部结构的地震动反应上,都跟集中质量模型吻合得较好,只是 6 弹簧模型所算出的自振频率偏高,这主要是由于 6 弹簧模型忽略了桩基质量和刚度矩阵的非对角元素引起的。而在结构的地震动反应上,都表现出一定的不足:6 弹簧模型虽能适当地模拟群桩基础,从而大大缩减体系自由度,但是总体上显得很粗糙,误差比较大;而等效嵌固模型在墩体结构和上部结构的地震反应表现出较好的精确性,但对桩基的模拟误差比较大,此外其模型比较简单,并且可以通过并桩大大缩减体系自由度,以提高计算效率;对于弹性嵌固模型,相对而言能较好地反映桩基的地震动反应,但是对基础以上结构的反应误差稍大,并且涉及到阻抗矩阵的计算略显烦杂。总之,这几种模型都有较好的实用性,也都各有利弊,如何选取合理的模型则依据工程的实际情况及要求而定。
参考文献
范立础. 桥梁抗震 [M]. 上海:同济大学出版社,1997. ↩
范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计 [M]. 北京: 人民交通出版社, 2001. ↩
Penzien J, Scheffey C F, Parmelee R A. Seismic analysis of bridges on long piles [R]. ASCE, 1964; 90(EM3): 223-254. ↩
Tim J, Ingham, Santiago Rodriguez, etc. Seismic analysis of bridges with pile foundations [J]. Computers and Structures, 1999; 72. ↩ ↩
叶爱君. 大跨度桥梁抗震设计 [D]. 同济大学博士学位论文, 1998.
陆锐. 群桩桥梁结构抗震简化计算方法的比较分析 [D]. 同济大学硕士学位论文, 2001. ↩
杨昌众. 桩基桥梁的场地判别和地震反应计算的实用简化方法 [D]. 同济大学博士学位论文, 1987. ↩
交通部公路规划设计院. 公路工程抗震设计规范 (JTJ 004-89) [S]. 北京:人民交通出版社,1990.
Clough RW, Penzien J. Dynamics of structures [R]. 2nd ed. McGraw-Hill, New York.
交通部公路规划设计院. 公路桥涵地基与基础设计规范(JTJ 024-85)[S]. 北京:人民交通出版社,1990.