鲁传安^1 胡世德^1 叶爱君^1
(同济大学土木工程防灾国家重点实验室,上海 200092)
摘要
大跨度高墩连续梁桥的抗震设计,特别是在高强度地震作用下的抗震设计,目前尚无规范可遵循。以国外某大桥为例,建立了全桥的动力分析模型,计算了结构的动力特性和地震响应,针对大桥在强震作用下主梁位移反应过大以及对支座抗剪要求过高的特点,讨论了采用粘滞阻尼器和双曲面球型减隔震支座的减隔震效果,研究结果表明这些措施是有效的,可为同类大跨高墩连续梁桥的抗震设计提供参考。
关键词
大跨高墩连续梁桥,强震,抗震性能,减隔震措施
Study on Seismic Performance for Long Span and High Pier Continuing Girder Bridges in Severe Earthquake Region
LU Chuanan^1 HU Shide^1 YE Aijun^1
(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract
At present, there is no seismic design code for long span and high pier continuing girder bridges, especially under severe earthquake. In this paper, a foreign bridge was taken as an example. The dynamic model of the bridge was introduced. Dynamic characteristics and seismic responses were analyzed. In allusion to the characteristics of too large displacement response of main girder and high demand of support resisting shear force, combination effect to adopt viscous damper and isolated support was discussed herein. The results show that these measures are effectual. This may be a reference for the seismic analysis of similar long span and high pier continuing girder bridges.
Keywords
long span and high pier continuing girder bridge, severe earthquake, seismic performance, isolated measure
1 引言
梁桥是我国最常用的一种桥型,地震灾害资料表明,梁桥的震害现象主要有落梁、桥台沉陷、墩柱的弯曲剪切破坏等,给社会带来巨大的生命财产损失。因此,对连续梁桥特别是大跨高墩连续梁桥的抗震性能进行研究,无论从经济角度还是从安全角度都显得特别重要。目前,无论国内还是国外对连续梁桥的抗震性能研究已经比较多了,但是对于高强度地震下的抗震性能研究还不多。国内外现有的绝大多数桥梁工程抗震设计规范只适用于中等跨径的普通桥梁,超过适用范围的大跨径桥梁的抗震设计,则无规范可循。如我国 **《公路工程抗震设计规范》(JTJ004-89)** 只适用于主跨不超过 150\text{m} 的梁桥和拱桥;美国 AASHTO 规范抗震设计篇中也规定,该规范只适用于钢与混凝土主梁与箱梁式桥,主跨不超过 150\text{m} 。因此,目前对于主跨超过 150\text{m} 的大跨度桥梁,一般都要专门立项,进行抗震研究。本文以国外某大桥为例,阐明大跨高墩连续梁桥在高强度地震作用下的地震响应,并重点探讨其减隔震措施。
2 工程背景
本文所研究的桥梁是国外某高速公路一期工程中的一座特大型桥梁。桥梁全长 348\text{m} ,其跨径组合为 89\text{m}+170\text{m}+89\text{m} 。桥址位于构造盆地的盆缘附近,距东侧倾斜岩层和堆积体仅 50\text{m} 左右,该处地质构造单一,岩层产状稳定且平缓,岩层节理裂隙较发育。桥址通过的地层为凝灰岩夹砂岩与凝灰角砾岩,岩性依次如下:凝灰质角砾岩为厚层状,致密坚硬,地貌上形成陡坎,河谷北岸具有代表性;砂岩为风化后表面呈黄褐色,厚层状致密坚硬,以公路边坡出露的具有代表性;凝灰岩为厚层状,比较坚硬。
桥梁上部结构箱梁采用分离式的单室单箱结构,分上下行布置,每幅箱梁梁宽 13\text{m} ,在墩顶、跨中及桥台的两幅主梁间设体外横隔板。下部结构桥墩采用单个空心薄壁墩,2 个桥墩的高度分别为 51\text{m} 和 31\text{m} ,基础为布置有抗拔桩的扩大基础,2 个桥墩基础全部位于稳定的基岩上。桥台为设有“碰及脱”构造的重力式桥台,台背处设有岩锚以抵抗地震时的水平拉力。在桥台处设有三防伸缩缝。全桥在高墩设置固定支座,低墩和桥台处设纵向滑动支座。
3 分析模型及动力特性
3.1 分析模型
本文分析采用 SAP2000 程序进行计算。上部结构根据两主梁分幅实际情况,采用双主梁模式,在程序中用三维梁单元模拟。两主梁在体外横隔板连接处处理为主从;下部结构的桥墩也采用三维梁单元模拟,本文近似考虑承台为刚体,承台与桥墩及桩顶的连接处理为主从关系。对于基础,考虑到本桥桥墩和桥台地基为稳定的坚硬岩石地基,故在桥墩承台底及桥台底处理为嵌固。支座模拟在滑动方向处理为相对自由,固定方向采用大刚度弹簧约束。上部结构的二期恒载按线性均布加到主梁上。全桥三维有限元模型见图 1 所示。
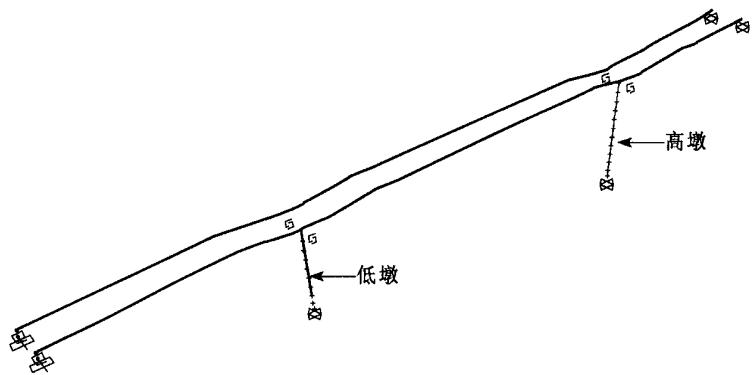
图 1 全桥动力计算模型
3.2 动力特性
分析和认识结构动力特性是进行抗震性能研究的基础,所以首先根据前面建立的动力计算模型分析桥梁结构的动力特性。表 1 为其前 10 阶的振型及对应周期。从表中可以看出,第 1 阶振型为主梁以固定墩为支点的顺桥向振动,周期3.908\text{s},因为纵向只有高墩处固定,其他均是自由的,故导致周期较长。横向振动出现在第 3 阶,周期1.120\text{s}。
表 1 结构的动力特性
| 振型阶数 | 周期/s | 振型描述 | 振型阶数 | 周期/s | 振型描述 |
|---|---|---|---|---|---|
| 1 | 3.908 | 主梁顺桥向振动 | 6 | 0.453 | 主梁高阶反对称侧弯 |
| 2 | 1.366 | 主梁对称竖弯 | 7 | 0.451 | 主梁高阶对称竖弯 |
| 3 | 1.120 | 主梁对称侧弯 | 8 | 0.357 | 主梁扭转 |
| 4 | 0.711 | 主梁反对称侧弯 | 9 | 0.326 | 主梁高阶反对称竖弯 |
| 5 | 0.666 | 主梁反对称竖弯 | 10 | 0.320 | 主梁高阶扭转 |
4 地震响应分析
目前,桥梁结构抗震性能的计算与分析主要采用反应谱与时程分析的方法。对于高强度的地震,国内外规范基本一致,均采用时程分析方法。因此,本文主要针对时程分析研究其抗震性能。
本桥的地震动加速度时程采用实测得到的强震记录,共有 3 个测点的实测地震波。其中,峰值最大地震波纵横向的加速度时程分别达到了 0.816g 和 0.796g。加速度时程曲线如图 2、图 3 所示。
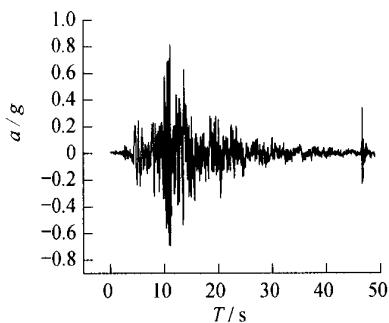
图 2 1084-1 纵向加速度时程
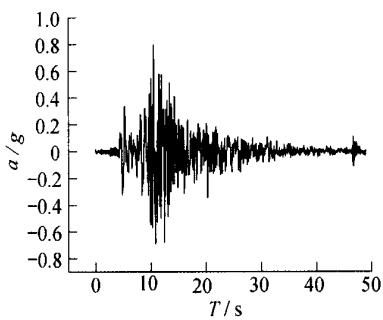
图 3 1084-1 横向加速时程
因 1084-1 地震波峰值最大,而又限于篇幅,本文在此只介绍结构在 1084-1 地震波下的时程结构反应及抗震措施。在时程分析过程中,考虑了滑动支座的摩擦耗能作用。滑动支座的恢复力模型可用双线性模式代表,其恢复力模型如图 4 所示。图中, E_{\max} 为临界摩擦力,X 为上部结构与墩顶的相对位移,x_y 为临界位移。弹性恢复力的最大值与临界滑动摩擦力相等,即
式中,f 为滑动摩擦系数;N 为支座所承担的上部结构恒载;x_y 为屈服位移。
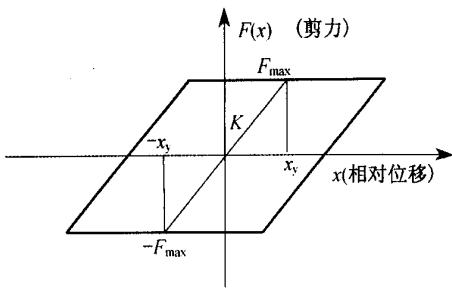
图 4 滑板支座恢复力模型
表 3、表 4 分别列出了具有代表性的桥墩墩底的内力响应及桥台、承台底反力。从分析结果中可以看出,不论墩底截面内力还是承台及桥台底反力,绝对值的量级均比较大。对于低墩,弯矩剪力的需求,横向要大于纵向。但是对于高墩,情况恰恰相反,原因在于高墩墩顶支座纵向为固定,而低墩则为滑动支座,导致纵向力大部分由高墩来承担。通过 ucfyber 程序(由美国加州大学 Berkeley 分校开发用于分析结构截面的软件)的弯矩曲率关系分析,发现低墩墩底横向和高墩墩底纵向均已屈服。
抗震分析中,支座也是我们关心的一个重要方面,固定支座的纵向剪力最大值已经达到 26400\text{kN},横向剪力最大值已经达到 31300\text{kN}。以上剪力已经远远超过支座的抗剪能力,故在强震作用下,对固定支座的抗剪能力要求比较高。
另外,梁端位移情况为,德黑兰端的主梁位移有 1.134\text{m},里海端主梁位移也达到了 1.123\text{m}。如果再加上考虑温度等其他因素影响,那么桥台位置处的伸缩缝宽将是非常之大,这是设计中不能接受的。
总之,通过地震响应分析,我们可以得到如下结论:第一,低墩墩底横向和高墩墩底纵向均已进入屈服状态;第二,固定支座的纵横向抗剪能力和纵向滑动支座的横向抗剪能力要求过高;第三,主梁梁端位移过大。
5 减隔震分析
针对以上地震响应特点,本文拟采取在两端桥台纵向加阻尼器及改固定支座为双曲面球型减隔震支座两种组合减隔震措施。其中,阻尼器的采用是为了控制梁端位移,大量研究表明,阻尼器是一种有效的位移控制措施,而采用减隔震支座目的是为了降低对固定支座抗剪能力要求。
5.1 阻尼器参数分析
阻尼器的设置首先就要涉及到阻尼器参数选取的问题,这就需要进行阻尼器参数分析。
本文采用粘滞阻尼器,阻尼器用 Maxwell 模型来模拟。阻尼力与速度的关系表达式为
式中,F 为阻尼力;\text{sgn} 为符号函数;v 为相对速度;C 为阻尼系数;\alpha 为速度指数。
阻尼系数 C 的取值对阻尼力 F 的影响很大,速度指数 \alpha 的取值直接决定阻尼器滞回曲线的形状。速度指数 \alpha 的常用值一般在 0.3\sim1.0 之间,\alpha 的取值越小,滞回曲线的形状越接近于矩形,即滞回曲线越饱满,其耗能能力越强,同时控制位移的能力也越强。因此,速度指数一般偏向于取小值。通过选取不同的阻尼器参数,计算结构的非线性时程地震反应,通过观察具有代表性的地震反应与阻尼器参数的变化规律,而找到一组合适的参数。此分析没有考虑减隔震支座的耗能作用。表 2 给出了阻尼器参数敏感性分析工况。
表 2 阻尼器参数敏感性分析工况设置
| \alpha | C=2000 | C=3000 | C=4000 | C=5000 | C=6000 | C=7000 |
|---|---|---|---|---|---|---|
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
图 5- 图 8 分别给出了低墩墩底截面弯矩与阻尼系数关系图、德黑兰端梁端位移与阻尼系数关系图、低墩墩底截面弯矩与速度指数关系图及德黑兰端梁段位移与速度指数关系图。图中,M 表示低墩墩底纵向弯矩,D 表示德黑兰梁端纵向位移,C 表示阻尼系数,\alpha 表示速度指数。
从图示分析结果可以看出,阻尼器对减小梁端位移有明显作用,同时对改善结构地震响应也很有利。从图 5 可以观察到,弯矩与阻尼系数并不是单调关系,弯矩随阻尼系数的增加,呈现出一种先降后升的趋势。从图 6 可见,德黑兰梁端位移随阻尼系数的增加而有明显减小。图 7 显示出,阻尼系数等于2000时,墩底弯矩随速度指数的增加而增加;大于2000时,墩底弯矩则先降后升。从图 8 可见,梁端位移随速度指数的增加而增加。总之,弯矩与阻尼系数及速度指数的关系不是一种单调关系,与以往的连续梁阻尼器参数分析得到它们之间的单调关系不同,值得关注。
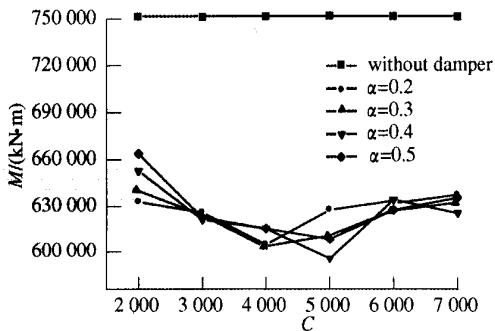
图 5 低墩墩底截面纵向弯矩与阻尼系数关系图
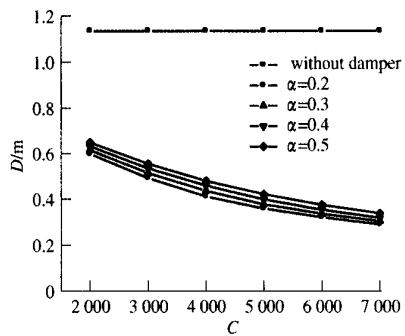
图 6 梁端纵向位移与阻尼系数关系图
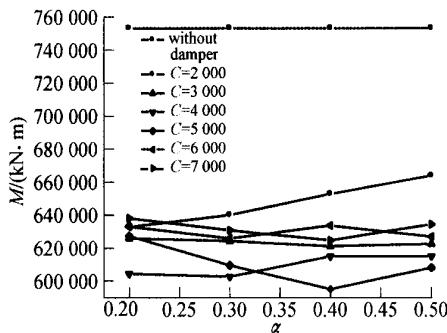
图 7 低墩墩底截面纵向弯矩与速度指数关系图
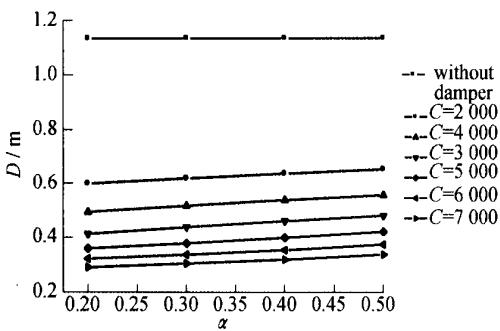
图 8 梁端纵向位移与速度指数关系图
综合抗震性能要求和经济因素等其他因素的考虑,本文建议采用的最终单个阻尼器参数为 C=6000, \alpha=0.3。
5.2 阻尼器与减隔震支座组合效果分析
本文拟将固定支座改为减隔震支座,为满足桥梁在正常使用荷载状态下受力和位移要求,减隔震支座在纵横桥向固定支座设置有剪力销,正常使用条件下保持工作状态,在高强度地震作用下,允许其剪断,此时,减隔震支座发挥减震耗能性能。本文减隔震支座剪力销的抗剪能力根据反应谱分析所得到的支座剪力来确定,即 2 个桥台处支座取 3000\text{kN},高墩支座取 5000\text{kN},低墩支座取 8000\text{kN}。
通过只加阻尼器的非线性分析知道,高墩纵向弯矩已减小很多,墩底截面能保持在弹性范围内。纵向固定支座剪力也有大幅减小,但是仍然大于支座的抗剪能力。同时横向固定支座的剪力没有减小。故纵横向固定支座的抗剪能力均不能满足要求,那么就要在加阻尼器的同时考虑加减隔震支座的措施。本文采用双球曲面球型减隔震支座,这是近年由同济大学桥梁抗震研究室与中国船舶重工集团第七二五研究所共同研发的一种减隔震支座。双曲面球型减隔震支座的减隔震原理与 FPI 支座的工作原理相类似,是将球型滑动支座的滑动面改为曲面而发展成的一种隔震支座(图 9),它包括一个具有双球面的球体、球形铸钢滑动曲面和球形铸钢转动面。支座可以在任何方向滑动,其尺寸主要由最大设计位移控制。通过结构自重提供所需的自恢复能力,帮助上部结构回到原来的位置。物理模型如图 10 所示,可描述为如下:
支座受力 F=K_2 d+F_p。其中,K_2 为屈后刚度,d 为位移,F_p 为支座的滞回受力;K_2 可由 K_2=W/R 求出;W 为支座恒载轴力,R 为支座半径。
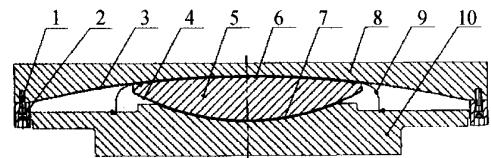
图 9 双曲面球型减隔震支座
1—抗剪栓;2—限位环;3—上球面不锈钢滑板;4—下球面不锈钢滑板;5—中座板;6—上圆氟滑板;7—下四氟滑板;8—上座板;9—密封裙;10—下座板
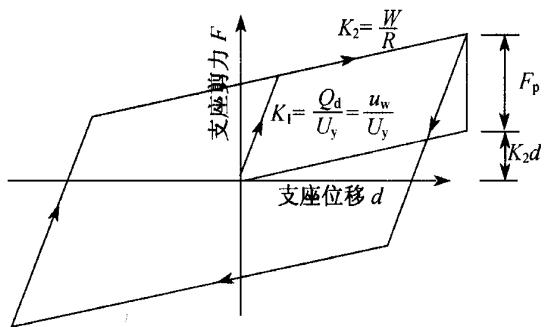
图 10 减隔震支座物理模型参数关系
对于减隔震支座屈服后的刚度 K_p,经过初步分析,根据公式确定取值为:高墩墩顶支座纵向及高低墩墩顶支座横向刚度取为 8000\text{kN/m},桥台支座横向刚度取为 2000\text{kN/m}。表 3、表 4 分别列出了采用双重减隔震措施的墩底截面内力、承台底和桥台底反力。
表 3 非线性时程分析墩底截面内力最大值
| 位置 | 方向 | 无减隔震措施 | 加阻尼器与减隔震支座 |
|---|---|---|---|
| 轴力/kN | 剪力/kN | ||
| 低墩墩底 | 纵向 | 7.78\times 10^3 | 3.38\times 10^4 |
| 横向 | 1.19\times 10^3 | 1.33\times 10^5 | |
| 高墩墩底 | 纵向 | 8.90\times 10^3 | 1.12\times 10^5 |
| 横向 | 1.80\times 10^3 | 9.89\times 10^4 |
表 4 非线性时程分析承台底及桥台底反力
| 位置 | 方向 | 无减隔震措施 | 加阻尼器与减隔震支座 |
|---|---|---|---|
| 轴力/kN | 剪力/kN | ||
| 德黑兰桥台 | 纵向 | 1.53\times 10^3 | 9.05\times 10^1 |
| 横向 | 1.08\times 10^4 | 2.01\times 10^4 | |
| 里海桥台 | 纵向 | 3.47\times 10^3 | 9.03\times 10^1 |
| 横向 | 2.33\times 10^3 | 1.15\times 10^4 | |
| 高墩承台 | 纵向 | 8.92\times 10^3 | 1.60\times 10^5 |
| 横向 | 1.87\times 10^3 | 1.39\times 10^5 | |
| 低墩承台 | 纵向 | 7.92\times 10^3 | 9.40\times 10^4 |
| 横向 | 1.20\times 10^3 | 1.80\times 10^5 |
与没有采取减隔震措施的结果相比,采用了减隔震措施后,由于两种减隔震方案共同作用,桥墩水平向剪力和弯矩产生了大幅度下降。桥墩承台底反力也有类似的结论。通过验算,关键截面保持在弹性范围内。桥台底纵向水平反力由于采用了阻尼器,导致反力有大幅增加。但是,这使得纵向力分配均匀了。而横向水平反力,由于采用了减隔震支座,导致其反力有一定程度减小。
从表 5 中可以看出,采用纵向阻尼器装置后,滑动支座的纵向位移有较大幅度下降,梁端纵向位移也减小了很多。但是,采用减隔震支座后,一旦销子剪断,在纵横向都会产生一定数量的屈后位移,这就要求支座和墩顶的尺寸都要满足抗震设计的要求,这在一定程度上增加了造价。不过它能大大减缓桥墩受力。所以,抗震中,往往通过牺牲一小部分,来合理地达到保护结构的目的。
表 5 非线性时程分析支座位移 (m)
| 支座位置 | 无减隔震措施 | 加阻尼器与减隔震支座 |
|---|---|---|
| 纵向位移 | 横向位移 | |
| 德黑兰桥台 | 1.1328 | 0.0002 |
| 里海桥台 | 1.1266 | 0.0001 |
| 高墩墩顶 | 0.0005 | 0.0004 |
| 低墩墩顶 | 1.1214 | 0.0005 |
综上所述,本桥即使是在高强度地震作用下,通过合理地加阻尼器和采用减隔震支座,也能很好地控制结构的内力与位移。
6 结论
本桥通过采用三维有限元建立全桥模型,并重点分析结构在高强度地震下的反应及减隔震措施,得到以下结论:
(1)对于峰值达到 0.816g 地震作用下,仅考虑滑动支座的摩擦耗能作用,结构的地震响应仍然很大,如墩底弯矩最大值已经达到 1\times 10^6\text{kN}\cdot\text{m} 的量级,特别是梁端位移有 1.134\text{m}。关键截面已经屈服,支座的抗剪能力也远远不够。
(2)阻尼器参数分析,由于采用高峰值的加速度时程,与以前的连续梁阻尼器参数研究结论稍有不同,即关键截面弯矩与阻尼系数及速度指数的关系不再是单调关系。
(3)采用阻尼器与减隔震支座两种组合减隔震措施后,结构的地震反应大幅下降,并且受力分配均匀了,有利于结构受力,但是这些是以采用高的阻尼系数及大的减隔震支座屈服后位移为代价。所以,对于大跨度连续梁桥,在高强度地震下,对减隔震装置的参数要求比较高。
(4)在大跨度高墩连续梁桥遭受高强度地震时,通过合理地组合一些减隔震措施,能够较好地控制结构地震响应。
参考文献
- 范立础. 桥梁抗震[M]. 上海:同济大学出版社,1997.
- 范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计[M]. 北京: 人民交通出版社, 2001.
- 叶爱君. 桥梁抗震[M]. 北京:人民交通出版社,2002.
- 殷海军, 王志强, 胡世德. 连续梁桥设置阻尼器参数分析[J]. 同济大学学报(自然科学版), 2004, 32(11):1437-1441.
- 叶爱君, 华新, 韩大章. 灌河大桥抗震性能研究[J]. 公路, 2005(11):40-45.