王斌斌^1 袁建兵^2 刘延芳^1 叶爱君^1
(1. 同济大学土木工程防灾国家重点实验室, 上海 200092; 2. 上海市政工程设计研究总院, 上海 200092)
摘要
目前,大跨度钢桁架拱桥的抗震设计分析相对较少,无规范可遵循。以宁波城庄路姚江大桥为例,建立了主桥和引桥一体的动力分析模型,分析了桥跨结构的动力特性和地震反应,探讨了主、引桥相互间的影响作用,并比较了几种改善抗震性能措施的效果。罕遇地震下主桥纵向固定墩基础难满足抗震要求,可采用减震措施。
关键词
钢拱桥,结构模型,地震反应,相互作用,抗震性能
Study on Seismic Performance for Yaojiang Steel Arch Bridge
WANG Binbin^1 YUAN Jianbing^2 LIU Yanfang^1 YE Aijun^1
(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;
2. Shanghai Municipal Engineering Design General Institute, Shanghai 200092, China)
Abstract
At present, there are only few seismic designs on large steel arch bridges, and there are no seismic design specifications for reference either. In this paper, Ningbo Yaojiang steel arch bridge is taken as an example. The dynamic model of arch bridge including main bridge and approach bridges is introduced, dynamic characteristics and seismic responses are analyzed. Also the interactions of main bridge and approach bridges are discussed. And some kinds of measures that can improve aseismic performance are compared. The results show that under severe earthquake the pile foundation may not be safe and isolation design should be used. It is useful for similar seismic analysis.
Keywords
steel arch bridge, structural model, seismic response, interaction, seismic performance
1 概述
随着国民经济和桥梁建造技术的迅猛发展,越来越多的大跨度桥梁矗立在我国的大地上。大跨拱桥一般被用于跨越大江、大河或高沟、深谷,它是公路交通运输的枢纽和咽喉,也是公路工程中的生命线工程之一。同时,拱桥也是城市桥梁中的常用桥型之一,它具有外形优美、经济适用、承载潜力大等优点。从最近几次的地震灾害来看,其中多次破坏性地震都集中在城市,造成了非常惨重的生命和财产损失。因此,对大跨拱桥的抗震性能进行全面研究,不仅对保证公路交通的安全有重要意义,还对抗震救灾及灾区重建有重要的影响。
国内外现有的绝大多数桥梁工程抗震设计规范只适用于中等跨径的普通桥梁,大跨径桥梁的抗震设计则无规范可循。如我国《公路工程抗震设计规范》(JTJ004—89)只适用于主跨不超过 150\text{m} 的梁桥和拱桥;美国 AASHTO 规范中的抗震设计规范只适用于主跨不超过 150\text{m} 的钢与混凝土主梁与箱梁式桥,不适用于斜拉桥、悬索桥、拱桥以及活动式桥。因此,对于主跨超过 150\text{m} 的大跨度桥梁,目前一般都要进行抗震研究。本文以姚江大桥为例,阐述了钢桁架拱桥抗震分析的全过程,包括动力模型的建立、地震动输入和地震反应分析、抗震验算以及抗震措施的比较,并对值得关注的几个问题进行探讨。
2 动力分析模型及地震动参数
城庄路姚江大桥主桥处江宽 350\text{m} ,主桥采用下承式三跨连续钢桁架拱桥方案,跨径组合48\text{m}+180\text{m}+48\text{m}=276\text{m} ,主桥总宽 43.6\text{m} 。主桥拱肋由 2 片桁架和 6 道风撑组成,全桥呈密布 N 形钢桁架拱结构形式;风撑采用口字形形式,杆件采用工字形断面,一道风撑由 4 根直杆、上下联斜杆和前后联斜杆组成。主梁采用结合梁,桥面结构由钢系梁、钢横梁、人行道挑梁、钢小纵梁和钢筋混凝土桥面板组成。南北两侧引桥均为 28\text{m}+28\text{m} 的两跨连续梁,引桥端部搁置在主桥端横梁的牛腿上。主桥和引桥连接处设置伸缩量为 200\text{mm} 的梳齿板式伸缩缝。主桥主墩设置 4 个 4500\text{t} 钢支座,其中 1 个为固定支座,2 个为单向滑动支座,1 个为多向活动支座;主桥边墩采用1750\text{t}的纵向滑动钢支座。主墩基础和边墩基础均为哑铃形高桩承台。
2.1 动力分析模型
由于引桥与主桥之间存在耦联关系,动力特性和地震响应相互影响,因此,结构抗震研究需将主桥、引桥一起考虑进行结构建模,建立结构动力特性和地震反应分析的三维有限元模型(图 1)。
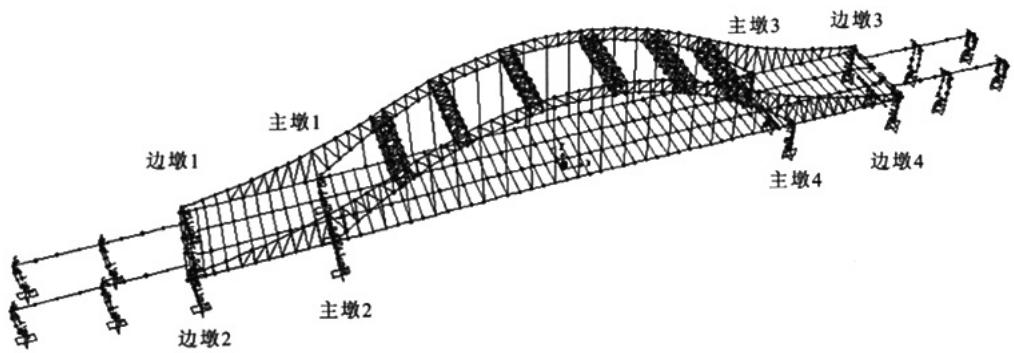
图 1 考虑引桥的拱桥动力计算模型
参照实际结构的布置,上部结构中桥面主梁主要采用两主梁模式,分析程序中用梁单元模拟;钢横梁由梁单元模拟;其中,混凝土桥面板是在系梁、横梁组成的梁格上布置,在建立模型过程中既要考虑到桥面的质量也要考虑桥面与主梁连接后具有一定刚度,因此,在分析程序中用面单元模拟;整个拱圈(包括风撑)都是用桁架单元模拟;吊杆也用梁单元模拟,但考虑恒载引起的几何刚度的影响。
下部结构中的桥墩也用梁单元模拟,承台近似按照刚体模拟,但需要特别说明的是哑铃形承台中联系梁相对刚度较弱,不能作为刚体部分,故按照实际截面模拟为梁单元。在桥梁的地震反应分析中,桩基础的一种常用处理方法是在承台底部加上 6 个方向的弹簧来模拟桩基础的作用,并由承台底部的内力按照静力方法反推单桩最不利受力。弹簧刚度根据土层状况和桩的布置形式按静力等效的原则确定,土性资料一般根据 m 法确定。其中,在动力特性和反应谱分析中,忽略滑动支座的摩擦作用,按墩、梁相互自由处理;而在时程分析中,采用非线性的恢复力模型考虑滑动支座的摩擦耗能作用。
2.2 地震输入
根据工程地震研究所提交的《工程场地地震安全性评价报告》(以下简称《安评报告》),工程场地水平加速度反应谱以地震影响系数的形式给出,其表达式为
式中,\alpha(T)为地震影响系数;A_m为设计地震动峰值加速度,g(1g=10 \text{m/s}^2);\beta(T)为设计地震动加速度放大系数谱;T为周期。
选取 100 年超越概率10\%(P_1)和 100 年超越概率3\%(P_2)作为地震动输入。P_1的A_m为0.095g,P_2则为0.131g。采用时程分析法对姚江大桥进行地震反应分析。分别对两个概率水平P_1和P_2的 6 组地震加速度时程进行了地震反应分析,分析结果取 6 组反应最大值的平均值。图 2 和图 3 分别画出了P_1概率水平的反应谱曲线和某加速度时程曲线。
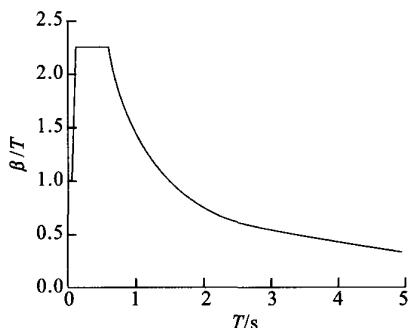
图 2 加速度放大系数反应谱曲线
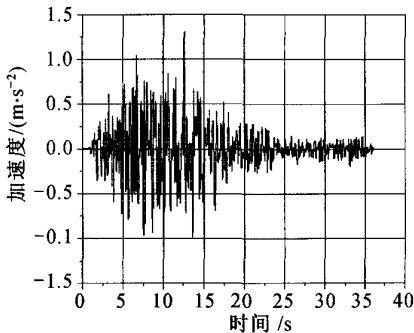
图 3 水平地震加速度时程
3 动力特性分析和地震反应分析
3.1 动力特性分析
根据前述的动力计算模式,对主桥结构进行动力特性分析。表 1 为姚江桥主桥的前 10 阶振型及对应的频率。从表中可以看出钢拱桥的第 1 阶振型一般为主拱圈的横向侧弯,周期为1.855\text{s}。第 3 阶为反对称竖弯,同时有固定墩的顺桥向振动。而主桥的对称竖弯出现在第 4 阶,周期为0.949\text{s},此振型也包含了固定墩的纵向振动。主桥的扭转出现在第 7 阶,周期为0.735\text{s}。
3.2 地震反应分析
采用反应谱方法与非线性时程方法分别对主、引桥进行了地震反应分析。输入的反应谱采用两个超越概率水平的地震加速度反应谱,取前 400 阶振型,按 CQC 法进行组合。地震输入采用两种方式:①纵向 + 竖向;②横向 + 竖向。方向组合采用 SRSS 方法。由于《安评报告》没有给出竖向的地震加速度反应谱,故偏安全地采用水平向的加速度反应谱,竖向地震加速度峰值取水平向的0.67倍。
分析结果表明,拱桥上部的钢桁架结构在两种概率水平下地震反应结果一般处于较低水平,恒载与地震荷载组合后各控制截面满足要求。因此,以下分析主要集中于桥梁的下部结构地震反应。表 2 列出了桥墩和承台底的内力,表中的墩和基础的编号见图 1 所示。由于加速度时程曲线转换成的反应谱曲线落在设计反应谱曲线的下侧,所以,无论是纵桥向输入还是横桥向输入,时程的结果一般略小于反应谱的结果,两者变化规律相似。对应于同一种输入,纵桥向的固定墩处弯矩远大于其他滑动墩处弯矩,而同为滑动墩的内力基本相同;横向输入时也有同样规律,即横向固定墩处弯矩很大,其为控制截面位置。同一侧墩底截面内力相差很大,而通过横梁的分配传递到承台底时内力相差程度有所减小。限于篇幅,表格中仅列出部分控制截面。
表 1 主桥结构的动力特性
| 振型阶数 | 周期/s | 振型描述 |
|---|---|---|
| 1 | 1.855 | 主拱对称横向侧弯 |
| 2 | 1.084 | 主拱反对称横向侧弯 |
| 3 | 1.076 | 反对称竖弯 |
| 4 | 0.949 | 对称竖弯+固定墩纵振 |
| 5 | 0.789 | 高阶对称侧弯 |
| 6 | 0.751 | 拱圈高阶对称侧弯 |
| 7 | 0.735 | 拱圈高阶对称侧弯 |
| 8 | 0.707 | 高阶对称竖弯 |
| 9 | 0.676 | 拱圈高阶对称侧弯 |
| 10 | 0.652 | 拱圈高阶对称侧弯 |
表 3 对下部结构的地震反应进行了验算。验算的是承台底各单桩承受的轴力较小而地震弯矩比较大的最不利工况,结果表明纵向 + 竖向输入下反应相对比横向 + 竖向输入下的反应大。所以,表中只列出了纵向 + 竖向输入的结果。同时考察在常规配筋率1.4\%的情况下最不利单桩的屈服弯矩,主承台 1 底下桩略不能满足要求,相差大概20\%。通过适当增加桩身配筋率到1.75\%,屈服弯矩变为5054\text{kN}\cdot\text{m},能满足要求。
地震中支座是易损构件之一。此桥在地震反应下,无论纵向固定支座还是横向固定支座的地震力都比较大,地震力 / 吨位从0.15到0.46不等,最不利的是P_2地震水平下边墩 3 上的支座,横向地震力 / 吨位达到了0.46,应注意增大支座水平抗力以满足要求。
表 2 下部结构地震反应 (P_2 纵向 + 竖向)
| 截面位置 | 反应谱法 | 时程分析法 |
|---|---|---|
| 轴力/kN | 剪力/kN | |
| 边墩1底 | 1689.9 | 735.7 |
| 边墩3底 | 1765.0 | 739.4 |
| 边承台1底 | 2503.7 | 3507.1 |
| 边承台3底 | 2571.4 | 3506.7 |
| 主墩1底 | 4702.2 | 15854.2 |
| 主墩3底 | 4322.8 | 1344.9 |
| 主承台1底 | 5672.1 | 17601.2 |
| 主承台3底 | 5369.3 | 7344.3 |
表 3 各承台底最不利单桩截面强度验算
| 截面位置 | 最小轴力/kN | 需求弯矩/(kN·m) | 屈服弯矩/(kN·m) |
|---|---|---|---|
| 边承台1底 | 1861 | 2006 | 5492 |
| 边承台3底 | 1899 | 1944 | 5510 |
| 主承台1底 | -1045 | 4923 | 4009 |
| 主承台3底 | 3484 | 2239 | 6236 |
4 主、引桥地震耦联性影响分析
本例中相邻引桥连续梁搁置在主桥端横梁上,因此在地震作用下,主桥及其引桥是共同振动的,它们的地震反应是相互影响的。这种耦联作用性不仅会改变各自的振动特性,还会改变各自的地震反应。而且,在地震作用下,主、引桥之间会产生相对位移,如果位移过大会引起碰撞、落梁等破坏。为此,在前述已经考虑主、引桥共同作用的分析基础上,研究引桥对主桥的内力位移影响是非常必要的。以下分别比较了两种超越概率地震作用下以及两种地震输入下的地震反应。
考察纵向 + 竖向输入时两种概率水平下连接处相对位移,可以看出,P_1概率地震水平下最大位移为4.8\text{cm},P_2概率地震水平下最大位移为9.0\text{cm},均小于伸缩缝宽度。表 4 和表 5 分别列出了纵向 + 竖向以及横向 + 竖向输入下主桥、全桥地震反应比较。从表 4 可以看出,由于引桥通过纵向滑动支座与主桥连接,所以两者纵向几乎没有影响。边墩底和边承台底地震轴力因为与墩顶质量有关,所以变化较大,而主墩底和主承台底地震轴力变化很小;单独引桥和主引桥两种模型的墩底、承台底的剪力和弯矩变化很小,可以认为不受影响。地震作用下主、引桥连接处会产生相对位移,如果位移过大,则会造成伸缩缝破坏,产生碰撞或者落梁,从前述分析可以看出,此时纵向相对位移较小,满足要求。
表 4 主、引桥相互作用地震力比较(纵向 + 竖向)
| 截面位置 | 主桥单独作用结果 | 主、引桥相互作用结果 |
|---|---|---|
| 轴力/kN | 剪力/kN | |
| 边墩1底 | 714.8 | 753.3 |
| 边墩3底 | 765.9 | 776.2 |
| 边承台1底 | 1135.3 | 2163.9 |
| 边承台3底 | 1265.3 | 2206.9 |
| 主墩1底 | 3014.5 | 7123.4 |
| 主墩3底 | 2334.2 | 1858.9 |
| 主承台1底 | 3710.7 | 8173.4 |
| 主承台3底 | 3389.4 | 4105.8 |
从表 5 可以看出,横桥向输入下主桥受引桥的影响很大,特别是引桥横向固定支座处的主桥 1、3 号边墩和相应的承台底地震反应。此时,主、引桥模型比单独主桥模型的地震反应增大比率最大有 1 倍多。同时,单独主桥中,边墩处地震反应基本相同,由于南北引桥结构和地质条件等的不对称,引起主、引桥模型中主桥 1、3 号边墩的反应相差比较大。
表 5 主、引桥相互作用地震力比较 (横向 + 竖向)
| 截面位置 | 主桥单独作用结果 | 主、引桥相互作用结果 |
|---|---|---|
| 轴力/kN | 剪力/kN | |
| 边墩1底 | 495.5 | 2842.7 |
| 边墩2底 | 828.6 | 507.8 |
| 边承台1底 | 1279.0 | 3055.3 |
| 边承台2底 | 1309.0 | 3069.6 |
| 主墩1底 | 3011.1 | 6542.9 |
| 主墩2底 | 2932.1 | 789.4 |
| 主承台1底 | 4917.1 | 4910.3 |
| 主承台2底 | 4331.3 | 4959.5 |
5 主桥减震研究
以上的主桥抗震分析都是在通常约束条件进行的,即主、引桥各支座采用固定或滑动钢支座,很大程度下能够满足结构的抗震安全问题。但是,在P_2概率水平的纵向 + 竖向地震输入作用下,主桥固定墩处的承台底最不利单桩的抗弯强度不能满足要求,因此,为了较好地解决主桥的抗震问题,本文对其改善方案进行了探讨。
5.1 减震耗能支座方案
滑动摩擦支座本身是很好的减震耗能支座,主要缺点是没有自恢复力。因此,只要对滑动摩擦支座加以适当地改造,使其并联一个能提供一定刚度的构件,即可得到具有较好的减震耗能作用的钢支座,对应的滞回曲线呈双线性。现拟将纵向固定支座(即主墩 1,2 顶的支座)替换为减震支座,为满足桥梁在正常使用荷载状态下受力和位移要求,减震支座在纵桥向设置有固定销,固定销的抗力满足正常使用状态,在地震作用下,允许其剪断,此时减震支座发挥减震耗能性能。
对于摩擦支座滑动后的刚度K_p,经过初步分析,确定主桥原纵向固定支座刚度取值4.2 \text{E}+03 \text{kN/m}。采用P_2下 6 条地震加速度时程作为输入,进行非线性时程反应分析,以检验上述减震支座的减震效果。表 6 列出了各墩底和承台底的内力反应,与采用固定或滑动钢支座时同样概率水平的地震反应结果 (表 2) 相比,结果表明:采用减震耗能支座后,原纵向固定墩底、承台底的地震反应的轴力变化很小,剪力和弯矩分别减小大约57\%和82\%。因此,采用减震耗能支座不仅能对桥墩和基础起到很好的保护作用,而且导致的支座和伸缩缝处位移不大,能较好地解决主桥纵向输入下的抗震问题,是一个值得推荐的结构体系。
表 6 各承台底内力最大值
| 截面位置 | 轴力/kN | 剪力/kN | 弯矩/(kN·m) |
|---|---|---|---|
| 边承台1底 | 2058.6 | 3098.8 | 8342.6 |
| 边承台3底 | 2121.7 | 3017.9 | 8254.6 |
| 主承台1底 | 5003.7 | 5857.5 | 20701.8 |
| 主承台3底 | 4677.8 | 5605.3 | 20372.8 |
5.2 阻尼器方案
阻尼器的种类较多,有铅挤压阻尼器、钢阻尼器、摩擦阻尼器以及油阻尼器等。其中,油阻尼器的阻尼力只与速度有关,可以减小结构的变形和内力。相对来说,油阻尼器比较有优势,而且在大跨度桥梁上的应用也比较多。所以,主要研究油阻尼器的阻尼效果。
现拟在主桥主墩 3,4 的纵向滑动支座处添加安装油阻尼器,C=4000, \alpha=0.4。同样采用P_2概率水平的 6 条地震加速度时程作为输入,进行非线性时程反应分析,以检验所加阻尼器的效果。表 7 列出了各墩底和承台底的内力反应,与采用固定或滑动钢支座时同样概率水平的地震反应结果 (表 2) 相比,结果表明:采用阻尼器后,原纵向固定墩底、承台底的地震内力有所减小。分别对控制设计的各桩基础进行强度验算,均保持弹性工作状态。
表 7 各承台底内力最大值
| 截面位置 | 轴力/kN | 剪力/kN | 弯矩/(kN·m) |
|---|---|---|---|
| 边承台1底 | 2224.0 | 2956.6 | 8347.0 |
| 边承台3底 | 2104.3 | 2959.2 | 8293.9 |
| 主承台1底 | 5286.1 | 10855.0 | 93782.2 |
| 主承台3底 | 4800.4 | 6437.8 | 40023.6 |
6 结论
本文采用钢桁架拱桥和引桥模型,分析了钢桁架桥的地震反应,可以得出以下结论:
(1)在P_1概率地震动输入下,主拱上部钢桁梁的应力均小于其屈服应力,上部钢桁梁在弹性范围内工作,固定主墩和桩基础也在弹性工作状态。
(2)在P_2概率地震动输入下,主拱上部钢桁梁仍保持在弹性工作范围。另外,时程分析表明,纵桥向考虑活动支座的摩擦耗能时,固定墩所受的弯矩减小,处于弹性工作状态,最不利单桩进入屈服阶段。此外,主桥支座位移满足要求,但其横向抗力不足。结构中承台间联系梁起着传递和均匀地震内力的作用。
(3)经分析,主桥与引桥的相互耦联作用对主桥有一定影响,尤其在横向地震作用下,主桥边墩地震内力会增大。同时,主引桥相对位移均不超过9\text{cm},满足伸缩缝处位移要求。
(4)经抗震分析表明,两种概率地震作用下结构总体上可以满足抗震要求,但在P_2概率地震作用下固定墩处桩基础不能满足要求。分别采用减震支座方案与阻尼器方案后,结构的固定墩均能满足抗震要求;相比较而言,减震耗能支座方案效果更好。
参考文献
- 范立础. 桥梁抗震[M]. 上海: 同济大学出版社, 1997.
- 范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计[M]. 北京: 人民交通出版社, 2001.
- 叶爱君. 桥梁抗震[M]. 北京:人民交通出版社,2002.
- 同济大学土木工程防灾国家重点实验室. 宁波城庄路姚江大桥结构抗震性能分析研究[R]. 上海:同济大学,2006.