吴陶晶^* 王斌斌

（同济大学桥梁工程系, 上海 200092）

摘要

推导了以体系绝对位移形式表达的行波作用下结构的运动方程，利用大型结构分析软件SAP2000对三塔斜拉桥的地震反应的行波效应进行了时程分析的数值模拟，讨论了表面视波速对三塔斜拉桥行波输入下地震反应的影响，将其结果与一致激励时的结果进行比较并讨论了拟静力反应在总反应中的贡献，结果表明，在对三塔斜拉桥进行抗震设计时，应重视行波效应对边塔的不利影响。

关键词

行波效应，三塔斜拉桥，地震反应，一致激励，拟静力反应

Traveling Wave Effects on Seismic Responses of Three-Pylon Cable-Stayed Bridges

WU Taojing^* WANG Binbin

(Department of Bridge Engineering, Tongji University, Shanghai 200092, China)

Abstract

The dynamic equilibrium equation of structures considering traveling wave effects in the form of absolute displacement was deduced. The advanced finite element analysis software SAP2000 was successfully used to simulate traveling wave excitation in time history analysis of seismic responses of three-pylon cable-stayed bridges. The effect of apparent wave velocity on seismic responses of three-pylon cable-stayed bridges was investigated. The traveling wave result was compared with the uniform excitation result and the contribution of pseudo-static response to the whole response was discussed. The result showed that the adverse influence on side tower should be emphasized in seismic design of three-pylon cable-stayed bridges.

Keywords

traveling wave effect, three-pylon cable-stayed bridge, seismic response, uniform excitation, pseudo-static response

PDF BibTeX

1 引言

地震引起的地面运动在时间和空间上都具有高度的变化性，地震时从震源释放出来的能量以地震波的形式传至地表，而地表各点接收到的地震波是经由不同的路径、不同的地形地质条件到达的，因而反映到地表的地震动必然存在差异。对于大跨度桥梁，可能因地震波沿桥纵轴向先后到达的时间差，引起各支承处输入地震时程的相位差，简称行波效应。国内外许多学者研究表明行波效应对大跨斜拉桥地震反应有一定的影响（Abdel-Ghaffar¹,²,³、范立础⁴、秦权⁵等），但以上研究都是针对传统的两塔斜拉桥，而对于大跨多塔斜拉桥这一新型结构的研究较少。为了揭示行波作用下大跨多塔斜拉桥的地震反应规律，本文以某三塔斜拉桥为工程背景，分析了行波效应对大跨三塔斜拉桥地震反应的影响，探讨了行波效应对大跨三塔斜拉桥地震反应的影响机理，对三塔斜拉桥地震反应特性进行了研究。

2 考虑行波效应的运动方程

根据D'Alembert原理在惯性参照系中建立结构整体振动的以绝对位移表达的动力平衡方程⁶：

\begin{bmatrix} M_{ss} & M_{sg} \\ M_{gs} & M_{gg} \end{bmatrix} \begin{Bmatrix} \ddot{U}_s \\ \ddot{U}_g \end{Bmatrix} + \begin{bmatrix} C_{ss} & C_{sg} \\ C_{gs} & C_{gg} \end{bmatrix} \begin{Bmatrix} \dot{U}_s \\ \dot{U}_g \end{Bmatrix} + \begin{bmatrix} K_{ss} & K_{sg} \\ K_{gs} & K_{gg} \end{bmatrix} \begin{Bmatrix} U_s \\ U_g \end{Bmatrix} = \begin{Bmatrix} 0 \\ R_g \end{Bmatrix} \tag{1}

即

[M]\{\ddot{U}\}+[C]\{\dot{U}\}+[K]\{U\}=\{R\} \tag{2}

式中，[M],[C],[K] 分别为桥梁结构的质量矩阵、阻尼矩阵与刚度矩阵；\{\ddot{U}\}, \{\dot{U}\}, \{U\} 分别是节点的加速度矢量、速度矢量与位移矢量；\{R\} 是外荷载矢量。

若以角标 s 表示结构的自由度，角标 g 表示基础与结构相接触的自由度。相对于惯性参照系的各节点位移可以表示为如下两部分之和：

\begin{Bmatrix} U_s \\ U_g \end{Bmatrix} = \begin{Bmatrix} U_s^d \\ 0 \end{Bmatrix} + \begin{Bmatrix} U_s^* \\ U_g \end{Bmatrix} \tag{3}

式中，右边的第一项代表振动位移，第二项是拟静力位移，分别以上标 d 与 * 表示。拟静力位移的实质是超静定结构由于支座的不均匀沉降引起的结构位移，即使在一致激励时，拟静力位移也存在，但是由于所有支承处的拟静力位移都相等，对结构来说是刚体位移，不产生结构内力；而在非一致激励的情况下，各支承处的拟静力位移并不相等，从而在结构中产生内力。振动位移则是由于结构的惯性力引起的。

将式(3)代入式(2)并略去与振动有关的项，可得到结构的拟静力位移 U_s^*：

U_s^* = R_s U_g \quad R_s = -K_{ss}^{-1} K_{sg} \tag{4}

如果采用集中质量模型并略去阻尼的影响，得到求解振动位移 U_s^d 的方程：

M_{ss} \ddot{U}_s^d + C_{ss} \dot{U}_s^d + K_{ss} U_s^d = -M_{ss} R_s \ddot{U}_g \tag{5}

利用式(4)与式(5)求得拟静力位移 U_s^* 和振动位移 U_s^d 后，即可由式(3)求得结构的总位移 U_s，进而可以求出结构的内力。

将结构的绝对反应分成拟静力反应量和动力反应量时利用了叠加原理，由公式(3)可以看出，拟静力反应和动力反应均与结构刚度有关系，而结构进入非线性状态后，结构刚度与结构的绝对反应有关，此时拟静力反应和动力反应则不能分别单独求解，亦即叠加原理不再适用。因此，方程只能用于线性结构，而对于非线性结构则须直接采用结构的绝对位移为基本参量。

在多点输入的情况下，必须以不同支点的绝对地面运动的形式来反映，因此一般采用绝对位移法来建立动力方程。对于一个集中质量系统，动力平衡方程用结构内未知的节点位移 U_s、基础与结构相接触的节点指定绝对位移 U_g 的形式可写为

\begin{bmatrix} M_{ss} & 0 \\ 0 & M_{gg} \end{bmatrix} \begin{Bmatrix} \ddot{U}_s \\ \ddot{U}_g \end{Bmatrix} + \begin{bmatrix} C_{ss} & C_{sg} \\ C_{gs} & C_{gg} \end{Bmatrix} \begin{Bmatrix} \dot{U}_s \\ \dot{U}_g \end{Bmatrix} + \begin{bmatrix} K_{ss} & K_{sg} \\ K_{gs} & K_{gg} \end{bmatrix} \begin{Bmatrix} U_s \\ U_g \end{Bmatrix} = \begin{Bmatrix} 0 \\ R_g \end{Bmatrix} \tag{6}

只对结构共同平衡方程在基底结点指定的绝对位移可写成：

M_{ss} \ddot{U}_s + C_{ss} \dot{U}_s + K_{ss} U_s = -K_{sg} U_g - C_{sg} \dot{U}_g \tag{7}

通常忽略方程右边的阻尼力项，于是绝对位移运动方程简化为

M_{ss} \ddot{U}_s + C_{ss} \dot{U}_s + K_{ss} U_s = -K_{sg} U_g \tag{8}

式(8)即为多点非一致输入下结构的运动平衡方程，采用直接积分法进行非线性时程分析即可求得结构的绝对位移。采用结构绝对位移为基本参量的结构动力平衡方程由于没有采用叠加原理，因此其适用于非线性的地震反应分析。

3 分析模型与地震波

图1所示为某主跨为 418\text{m} 三塔斜拉桥的有限元模型，主梁在中塔处与塔柱固结，边塔、过渡墩和辅助墩处均采用滑动摩擦支座。计算时采用了结构分析软件SAP2000，其中，利用空间梁单元模拟主梁、主塔和墩柱，用空间杆单元模拟拉索；主塔和拉索均考虑恒载引起的几何刚度的影响。桥墩、桥塔与地面连接按“m”法计算得到的六向土弹簧进行处理。滑动支座用非线性连接单元模拟，其动力滞回曲线类似于理想弹塑性材料的应力-应变关系，如图2所示。

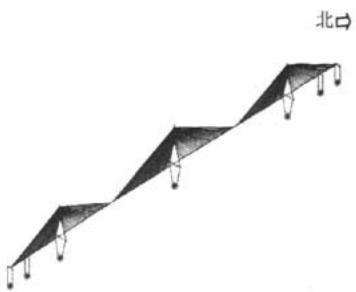
图1 某三塔斜拉桥分析模型

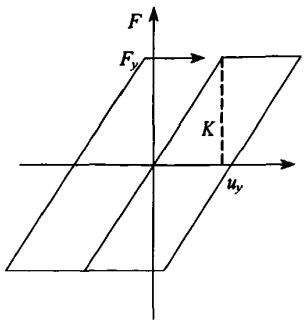
图2 滑板支座回复力模型

由于地震动的随机性，根据不同的地震动参数（震级、加速度峰值（PGA）、特征周期等）选取表1所示的7条地震波，并将加速度峰值调整到 0.4g，沿结构纵向输入。所选地震波的特征周期覆盖范围较大，在 0.12\sim0.88\text{s} 之间变化。

表 1 计算所用地震波

地震记录	震级	PGA/g	T_g/s	调幅系数
Northridge	6.7	0.25	0.88	1.63
Northridge	6.7	0.57	0.26	0.70
Kobe	6.9	0.50	0.44	0.80
Kobe	6.9	0.21	0.58	1.89
Loma Prieta	7.1	0.48	0.64	0.83
Whittle	6.0	0.30	0.34	1.34
San Fernando	6.6	0.17	0.12	2.30

为较全面地分析地震行波效应的影响，地震行进视波速依次取 500\text{m/s}, 750\text{m/s}, 1000\text{m/s}, 1500\text{m/s}, 2000\text{m/s}, 2500\text{m/s}, 3250\text{m/s} 和 4000\text{m/s} 对结构进行分析，由于结构的对称性较好，本次分析仅考虑地震波从南端向北端传播。

4 行波效应对三塔斜拉桥地震反应的影响

4.1 地震动行进波速对主塔内力反应的影响

图3给出了地震动行进波速的变化对各主塔塔底截面内力的影响。图中，纵坐标表示考虑行波效应与不考虑行波效应时地震反应的比值，\mu 为7条波的平均值，\sigma 为7条波的标准差。

从图3可以看出：当波速不断变化时，南塔塔底截面剪力比平均值变化区间为 0.889\sim1.070 弯矩比平均值变化幅度为 0.894\sim1.061；中塔塔底截面剪力比平均值变化幅度为 1.000\sim1.063，弯矩比平均值变化幅度 0.927\sim1.034；北塔塔底截面剪力比平均值变化幅度为 0.979\sim1.164，弯矩比平均值变化幅度为 0.969\sim1.224。考虑地震波的变异性，南塔塔底截面剪力最大增大 10\%，弯矩最大增大 15\%；中塔塔底截面剪力最大增大 16\%，弯矩最大增大 19\%；北塔塔底截面剪力最大增大 21\%，弯矩最大增大 19\%。

由图示结果可知，行波效应对不同部位的影响是不同的。其中，对边塔的影响比对中塔的影响显著；且行波效应倾向于减小地震动首先到达的边塔地震反应，增大地震动后到达的边塔地震反应。

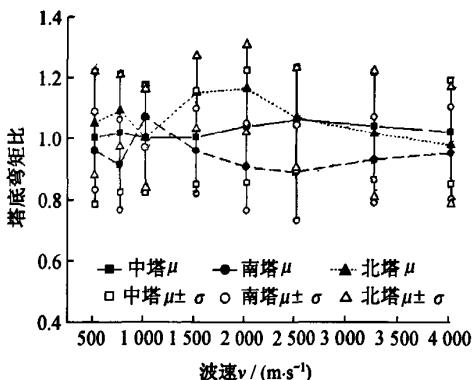
(a)

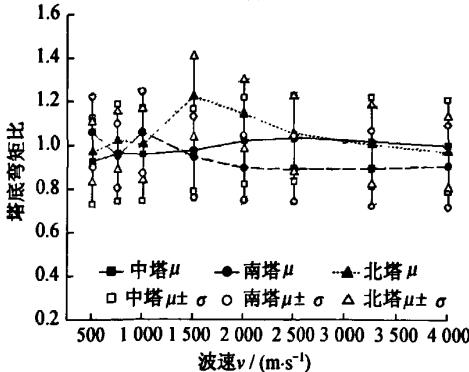
图3 地震行进波速对各主塔塔底截面内力的影响

4.2 地震动行进波速对基础地震反应的影响

图4分别给出了地震动行进波速的变化对各主塔承台底反力的影响。图中，纵坐标表示考虑行波效应与不考虑行波效应时地震反应的比值，\mu 为7条波的平均值，\sigma 为7条波的标准差。

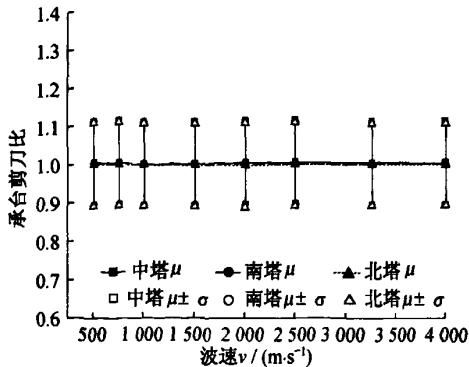
(a)

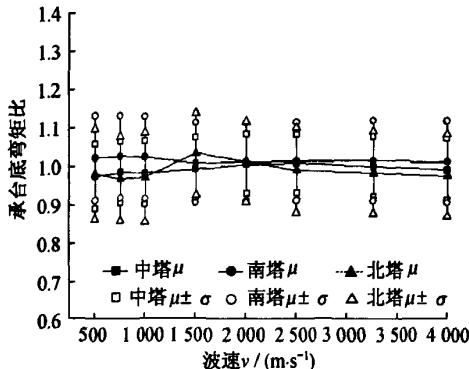
图4 地震行进波速对基础反力的影响

对比图3与图4可以看出，行波效应对各塔承台底基础所受剪力和弯矩的影响与对各塔塔底所受剪力和弯矩的影响规律基本一致，但影响程度均不大，即使考虑行波效应的变异性，剪力比平均值最大增大仅有 12\%，弯矩平均值最大增大仅有 14\%。

5 拟静力位移的贡献

对于线性结构，行波效应对结构反应的影响可以分为两部分：一为拟静力位移引起的反应；二为动力相对位移引起的反应。下面分析拟静力位移对结构的贡献。

图5显示了随着地震动行进波速的变化，拟静力位移对各主塔塔底地震反应的影响。从图5中可以看出：无论对剪力还是弯矩，拟静力位移对结构的影响随波速的增大而减小，并且所占比例很小，相比而言，剪力的影响更小。因此，大跨三塔斜拉桥这类较柔的结构来说，拟静力位移的影响是微弱的，也就是说行波效应对大跨三塔斜拉桥地震反应的影响主要由动力相对位移引起的。

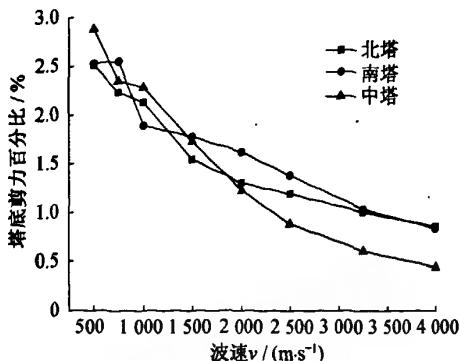
(a)

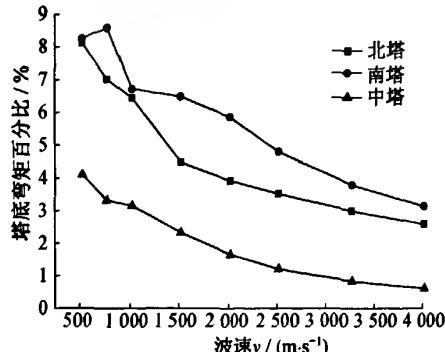
图5 拟静力分量对各主塔底截面内力的贡献

6 结论

行波效应对结构反应的影响机理是非常复杂的，它与地震动的频谱特性、结构的振动特性以及视波速等多个因素密切相关。通过以上分析可以得出以下结论：

（1）行波效应对边塔的地震反应有一定的影响，在个别波速情况下，行波效应使得边塔塔底反应增加 20\% 左右；而行波效应对中塔的地震反应影响不大。因此，应当重视行波效应对边塔的不利影响。
（2）行波效应对基础地震反应影响很小，因此，基础设计时可以不考虑行波效应对基础地震反应的影响。
（3）拟静力位移引起的反应对大跨三塔斜拉桥这类较柔的结构影响很小，行波效应对大跨三塔斜拉桥地震反应的影响主要由动力相对位移引起的。

参考文献

Nazmy A S, Abdel-Ghaffar A M. Effects of ground motion spatial variability on the response of cable-stayed bridges [J]. Earthquake Engineering and Structural Dynamics, 1992(21):1-21. ↩
Abdel-Ghaffar A M, Nazmy A S.3-D nonlinear seismic behavior of cable-stayed bridges [J]. Journal of Structural Engineering, 1991, 117(11):3456-3476. ↩
Abdel-Ghaffar A M, Nazmy A S. Seismic design of cable-stayed bridges: evaluation and research needs [C]. Proceedings ASCE Structures Congress, San Francisco, California, 1989. ↩
范立础, 衰万城, 胡世德. 上海南浦大桥纵向地震反应分析[J]. 土木工程学报, 1992, 25(3): 2-8. ↩
秦权, 孙晓燕, 贺瑞, 等. 苏通桥对非一致地震地面运动的反应和人工波质量的讨论[J].工程力学, 1992, 25(3):2-8. ↩
Clough R W, Penzien J. Dynamics of Structures [M]. New York: McGraw-Hill, 1960. ↩
李正农, 楼梦麟. 大跨度桥梁结构地震动输入问题的研究现状[J]. 同济大学学报, 1999, 27(5): 592-597.
陈幼平, 周宏业. 斜拉桥地震反应的行波效应[J]. 土木工程学报, 1996, 29(6): 61-68.
李忠献, 黄健, 丁阳, 等. 不同地震激励下大跨度斜拉桥的地震反应分析[J]. 中国公路学报, 2005, 18(3):48-53.