王靖程1, 叶爱君1, 王晓伟1, 李越2
(1. 同济大学土木工程防灾国家重点实验室,上海 200092;
- 凯斯西储大学土木与环境工程系,美国俄亥俄州克利夫兰市 44106)
摘要:在地震作用下,倾斜场地液化及其引起的侧向大变形会导致桥梁下部结构出现明显的残余变形,造成竖向承载能力损失,进而导致桥梁通行功能下降,因此很有必要对桥梁震后竖向承载能力的损失展开量化研究。本文首先介绍了典型的液化大变形场地桩柱式墩桥梁及其数值模拟方法,考虑结构、土体共 16 个参数的不确定性随机抽取了 80 个桥梁样本用于研究;然后,提出了增量动力分析 (IDA) 与竖向推覆 (Pushdown) 分析相结合的桥梁震后竖向承载能力损失分析方法;随后,结合典型工况的计算结果,分析了桥梁震后竖向承载能力损失的机理;最后,建立了基于桥墩残余漂移率的震后竖向承载能力损失量化回归模型和概率评估模型,并提出了面向震后承载能力损失的桥墩多级性能指标。结果表明:桩柱式墩的震后残余变形主要由砂土液化诱发的上覆土层侧向大变形引起;震后残余变形和 Pushdown 竖向加载过程中的 P-Δ 效应,是导致桥梁竖向承载能力损失的根本原因;竖向承载能力损失 5\% 、 20\% 、 35\% 和 50\% 对应的桥墩残余漂移率均值分别为 0.1\% 、 1.5\% 、 4.3\% 和 8.5\% 。研究成果可为我国液化大变形场地桩柱式墩桥梁的震后竖向承载能力评估与决策提供依据。
关键词:桥梁工程;桩柱式墩桥梁;竖向承载能力;损失评估;液化;增量动力分析;竖向推覆分析
中图分类号:TU473.1
文献标志码:A
doi: 10.6052/j.issn.1000-4750.2023.02.0073
LOSS ASSESSMENT OF POST-EARTHQUAKE VERTICAL LOAD-CARRYING CAPACITY FOR PILE-COLUMN BRIDGES IN LIQUEFIED GROUND WITH LARGE DEFORMATION
WANG Jing-cheng^1, YE Ai-jun^1, WANG Xiao-wei^1, LI Yue^2
(1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
- Department of Civil and Environmental Engineering, Case Western Reserve University, Cleveland, OH 44106, USA)
Abstract: Soil liquefaction and associated lateral deformation would trigger apparent residual deformation of pile foundations of the prevalent pile-column bridges, leading to a loss of vertical load-carrying capacity (VLC) and the degradation of serviceability. Therefore, it is necessary to investigate the loss of VLC after earthquakes. This study firstly introduces the typical pile-column bridges in liquefied ground with large deformation and the validated numerical modelling technique. In light of acknowledged high levels of uncertainties in soils, structures as well as ground motions, 80 bridges are sampled considering uncertainties of 16 structural and soil parameters. After that, a novel approach for quantifying the loss of VLC of bridges is proposed based on the incremental dynamic analysis (IDA) and Pushdown analysis. Then, the mechanism for the loss of VLC is investigated according to the results of an indicative case. Finally, based on the residual column drift ratio, a regression model and a probabilistic evaluation model, together with multi-level limit states are developed for estimating the loss of VLC. Results show that the significant post-earthquake residual column drift ratio is mainly triggered by the large soil deformation; this phenomenon together with the significant P- \Delta effect during the pushdown analysis results in the loss of VLC. Moreover, 5\% , 20\% , 35\% , and 50\% loss of VLC correspond to residual column drift ratios of 0.1\% , 1.5\% , 4.3\% , and 8.5\% , respectively. The research outcomes can be used for evaluating and decision-making of post-earthquake VLC loss of pile-column bridges in liquefiable ground with large lateral deformation.
Key words: bridge engineering; pile-column bridge; vertical load-carrying capacity; loss assessment; liquefaction; incremental dynamic analysis; pushdown analysis
我国沿海、沿江河地区存在大量桩柱式墩桥梁,桥址场地多为软土地基,含有饱和可液化砂土层1,2。历史震害3,4表明,砂土液化及其伴随的场地侧扩 (或通俗地称为液化大变形)5,6会导致桥梁桩基础出现明显的结构损伤和震后残余变形,造成桥梁的竖向承载能力损失。桥梁的震后竖向承载能力直接关系到桥梁的震后通行功能7,与人民的生命财产安全紧密相关。目前,桥梁震后通行决策主要是基于震后结构损伤的勘察结果做出的经验性判断8,具有高度不确定性,且桩柱式墩基础的结构损伤位于土面以下9,难以快速、准确地进行观察和测量。因此,有必要对液化大变形场地桩柱式墩桥梁的震后竖向承载能力损失进行快速定量评估,为更准确、可靠、高效的桥梁震后通行决策作支撑。
目前已有不少学者通过离心机试验10,11,12,13,振动台试验14,15,16,17,18,19,20,21,22,23,24,以及数值分析25,26,27,28,29,30,31,32,33,34等手段研究了液化大变形场地桥梁的抗震性能,但这些研究主要关注液化土体 - 桩相互作用以及桥梁构件的损伤和变形,专门针对桥梁震后竖向承载能力损失的研究极少。MACKIE 和 STOJADINOVIC 等7研究了美国加州非液化场地高速公路跨线桥的震后竖向承载能力;ARDAKANI 和 SAIIDI35发现,近断层地震作用下,桥墩在 1.2\% 的残余漂移率下仍可以承受较大的交通荷载;TERZIC 和 STOJADINOVIC36通过水平结合竖向拟静力试验发现,墩柱的位移延性系数为 4.5 时,竖向承载能力下降约 20\% 。然而,以上研究中桥墩墩底均作固结处理,没有考虑土 - 桩之间的竖向摩擦相互作用和地基的承载能力,不能反映桩基桥梁的真实竖向承载能力。鉴于此,ZHOU 等37,38展开了针对均匀干砂场地桩基础震后竖向残余承载能力的拟静力试验。WANG 等39采用数值分析手段揭示了液化侧扩流场地桩柱式墩桥梁震后损伤评估的最优工程需求参数 (EDP),即桩柱式墩的残余漂移率(震后墩顶与墩底位移差除以墩高)与桩身曲率具有较高的相关性。总体而言,现有研究缺乏针对液化大变形场地桩柱式墩桥梁震后承载能力损失的量化研究,难以支撑其震后承载能力评估和通行决策。
本文首先介绍典型液化大变形场地桩柱式墩桥梁及其有限元模型。然后,给出了一种基于增量动力分析 (IDA) 和竖向推覆 (Pushdown) 分析的震后竖向承载能力损失分析方法,并结合典型工况揭示承载能力损失的机理。最后,基于桥墩残余漂移率建立了震后竖向承载能力损失的量化回归模型和概率评估模型,并提出了液化大变形场地桩柱式墩面向震后竖向承载能力的多级性能指标。
1 研究对象及有限元模型
1.1 液化大变形场地桩柱式墩桥梁
本文研究对象为沿江沿海典型可液化微倾场地的桩柱式墩梁式桥,通常作为城市快速高架路 (如图 1(a)),抗震设防类别上一般属于 B 类(乙类) 或 C 类 (丙类) 桥梁。这类桥梁的场地和结构特征为:
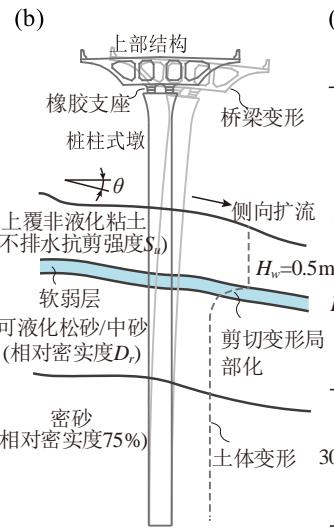
场地方面,自上而下通常由上覆非液化土层、可液化松砂 / 中砂层、以及密砂层构成,如图 1(b) 所示。地震下饱和砂土孔隙水上升,但由于上覆非液化土层的渗透系数很低,致使孔隙水聚集在上覆层与可液化层的交界面,形成抗剪强度很小的软弱层,导致上覆层在横桥向形成侧扩灾害。
结构方面,桩柱式墩埋置于密砂层中足够深度,即使在松砂 / 中砂层液化也不会出现明显的基础下沉现象26。出于设计和施工便利性,土面以下桩径与墩径相同,且由于桥梁跨径较小,各墩的场地条件、墩高和截面尺寸很接近,即各墩的动力特性相近。因此,此类桥梁的横桥向可简化为单墩模型进行抗震分析,主梁的惯性力通过固定型板式橡胶支座传递给桩柱式墩。

(a)

典型沿海沿江城市高架桥
(c)
图 1 研究对象及有限元建模
Fig.1 Study object and numerical modeling
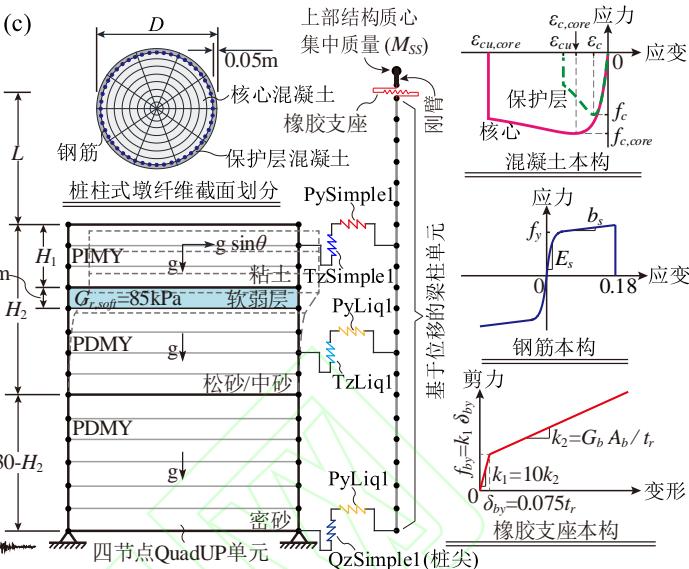
(a) 沿江沿海高架桥实例;(b) 液化大变形场地桩柱式墩桥梁单墩模型;(c) 有限元模型图示
1.2 有限元模型
基于 OpenSees 平台40建立的典型液化场地 - 桩柱式基础桥梁结构一体化有限元模型如图 1(c) 所示。土体采用基于平面应变理论的四节点 QuadUP 单元模拟,相同深度处土体节点共自由度,模拟土层的竖向压缩和水平剪切变形。土体底部节点约束水平与竖向自由度,作为假想基岩面输入地震波,故地震波应选取特征周期短、尽量接近岩石或坚硬场地特性的地震记录 (详见第 2 节)。粘土和砂土的力学本构分别采用 OpenSees 材料库中的 PIMY 和 PDMY 材料进行模拟,出于行文简洁考虑,土体材料本构的参数确定方法详见文献41。场地倾斜效应采用上覆粘土层的重力水平分力模拟,需要特别说明的是,WANG 等41基于三组不同离心机试验的数值模拟验证研究发现,软弱土层的厚度 h_w = 0.5\mathrm{m} ,参考剪切模量 G_{r,\text{soft}} = 85\mathrm{kPa} 可有效模拟上覆土层的侧扩位移。粘土与桩之间的侧向和竖向相互作用分别采用 PySimple1 以及 TzSimple1 材料模拟,而砂土与桩之间的侧向和竖向相互作用则分别采用可考虑孔隙水压影响的 PyLiq1 以及 TzLiq1 材料模拟,桩尖竖向土弹簧采用 QzSimple1 材料模拟。
主梁采用位于其质心处的集中质量进行模拟,质量通过墩柱截面面积、材料强度、轴压比计算确定。桩柱式墩采用基于位移的纤维梁柱单元模拟,每个单元设置 5 个积分点。纤维截面划分如图 1(c) 所示,钢筋和混凝土分别采用 Steel02 以及 Concrete04 材料模拟,钢筋受拉断裂应变为 0.18,采用 MinMax 本构模拟;核心混凝土本构参数根据 Mander 模型42确定,不考虑钢筋与混凝土之间的粘结滑移效应43。板式橡胶支座的本构采用双线性模型模拟,考虑了橡胶类支座拟静力试验中常见的初始大刚度效应;初始刚度 k_{1} 、弹性刚度 k_{2} 、刚度转换处的强度 f_{by} 和位移 \delta_{by} 的计算公式如图 1(c) 所示,其中橡胶支座总厚度 t_r = 76\mathrm{mm} 和剪切模量 G_{b} = 1200\mathrm{kN / m^{2}} 根据我国工程经验确定,支座面积 A_{b} 根据文献44计算确定。结构全局与局部坐标轴的转换采用可考虑大位移及 P-\Delta 效应的 Corotational 转换40。上述数值建模方法已通过多组离心机试验验证41,限于篇幅,验证结果在此不再赘述。
1.3 结构、场地参数不确定性
考虑到我国幅员辽阔,场地和桥梁各参数具有不同程度的不确定性,因此,本文全面考虑了场地和结构共 16 个参数的不确定性,涉及土层倾角、厚度、土体强度、截面尺寸、钢筋混凝土材料本构等参数,以尽可能覆盖工程实践中的常见情况。表 1 列出了不确定性参数的概率分布模型以及相应的均值、变异系数和参考文献。采用拉丁超立方抽样技术抽取了 80 个样本用于 IDA 和 Pushdown 分析,以建立基于桥墩残余漂移率的桥梁震后竖向承载能力损失的量化回归模型、概率评估模型、以及面向震后竖向承载能力的桩柱式墩多级性能指标。
Table 1 Uncertainty consideration of geotechnical and structural parameters
表 1 土体、结构不确定性参数
| 类别 | 参数 | 描述 | 概率分布模型 | 均值 | 变异系数(%) | 参考文献 |
|---|---|---|---|---|---|---|
| 场地 | Su/kPa | 粘土不排水剪切强度 | 对数正态分布 | 55 | 32 | 45 |
| Dr/(%) | 液化土相对密实度 | 正态分布 | 37 | 19 | 45 | |
| H1/m | 粘土层底部深度 | 对数正态分布 | 3.1 | 56 | 46 | |
| H2/m | 液化土层底部深度 | 对数正态分布 | 5.2 | 30 | 46 | |
| \theta/(^\circ) | 土面倾角 | 均匀分布 | (0°,6°)* | 47 | ||
| 结构 | D/m | 墩柱直径 | 正态分布 | 2 | 10 | 48 |
| L/m | 墩柱土面以上高度 | 正态分布 | 6.5 | 26 | 49 | |
| \alpha | 墩柱轴压比 | 正态分布 | 0.06 | 12 | 49 | |
| \rho_l/(\%) | 纵筋配筋率 | 正态分布 | 1.5 | 27 | 49 | |
| \rho_s/(\%) | 箍筋配筋率 | 正态分布 | 0.5 | 42 | 50 | |
| fc/MPa | 保护层混凝土强度 | 对数正态分布 | 34 | 18 | 51 | |
| \varepsilon_c | 保护层混凝土峰值应变 | 对数正态分布 | 0.002 | 20 | 51 | |
| \varepsilon_{cu} | 保护层混凝土极限应变 | 对数正态分布 | 0.005 | 20 | 51 | |
| fy/MPa | 钢筋屈服强度 | 对数正态分布 | 400 | 5 | 52 | |
| Es/GPa | 钢筋弹性模量 | 对数正态分布 | 200 | 3.3 | 51 | |
| bs | 钢筋硬化率 | 对数正态分布 | 0.01 | 20 | 51 |
*: 均匀分布参数 \theta 的上、下限
2 基于IDA和Pushdown的震后竖向承载能力损失分析方法
本文提出一种 \mathrm{IDA}53与 Pushdown 分析相结合的桥梁震后竖向承载能力损失评估方法,分析框架如图 2 所示。
IDA 是将地震动输入调至不同强度分别对结构进行动力时程反应分析以获得结构不同程度地震损伤的分析方法。回顾 1.2 节,输入地震波应选取特征周期短、接近岩石或坚硬场地特征的地震记录,因此,本文采用 BAKER 等54选取的 80 条岩石或坚硬场地实际地震记录作为 IDA 的地震动输入,其加速度反应谱、均值谱与我国规范55 \mathrm{I}_0 类 (坚硬) 场地设计反应谱的比较如图 3 所示。80 条实际地震记录反应谱基本介于本文研究对象 E2 设防等级的最大 (9 度区 B 类桥梁)、最小(6 度区 C 类桥梁) 设计反应谱之间,中位值与研究对象最常见的 7 度区 B 类桥梁设计反应谱很接近。将 80 条地震记录与 80 个桥梁样本进行随机匹配,开展 IDA。基于文献中液化场地桥梁概率地震需求模型的最优地震动强度指标 (IM) 相关研究56,57,58,采用峰值地面速度 (PGV) 作为 IM 对 IDA 中所需的地震动输入进行缩放,即将加速度地震记录的 PGV 分别缩放至 2.5\mathrm{cm/s}、5\mathrm{cm/s}、10\mathrm{cm/s}、15\mathrm{cm/s}、20\mathrm{cm/s}、25\mathrm{cm/s}、30\mathrm{cm/s}、35\mathrm{cm/s}、40\mathrm{cm/s}、50\mathrm{cm/s}、60\mathrm{cm/s} 以及 80\mathrm{cm/s}。缩放以 PGV=80\mathrm{cm/s} 为止的理由:一是该地震动强度已是历史震害中的较高值59,二是该强度可诱发桩柱的塑性变形。具体地,为获得目标 PGV 下的加速度地震动,先通过积分方法求出原始地震记录的 PGV,再计算达到目标 PGV 需要的缩放系数,最后将原始地震记录乘上该缩放系数。
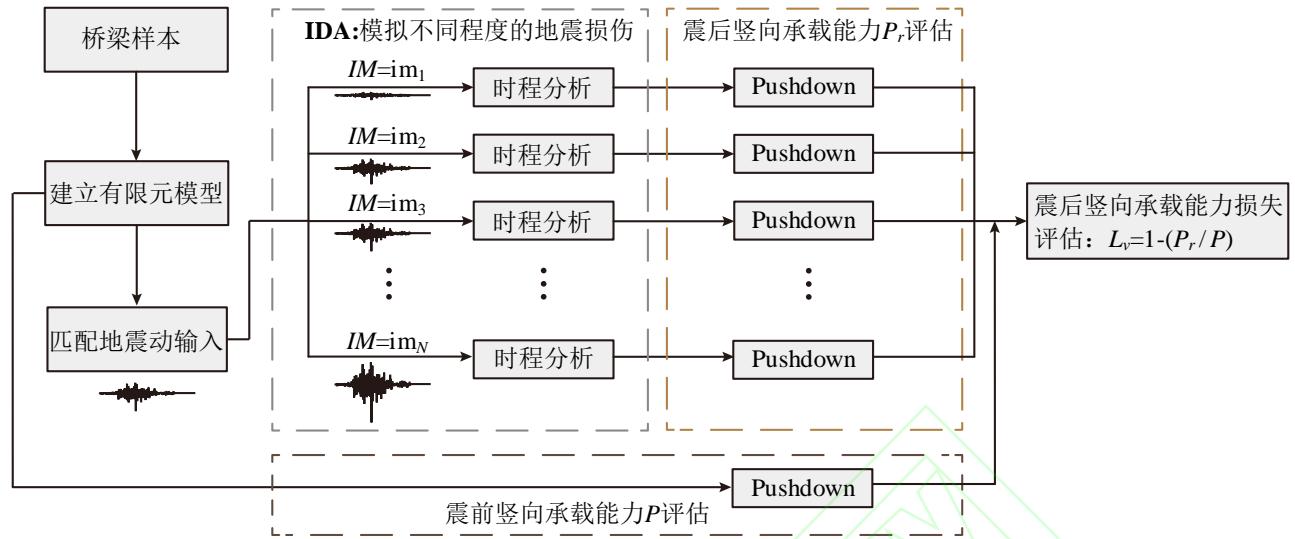
图 2 桥梁震后竖向承载能力损失分析框架
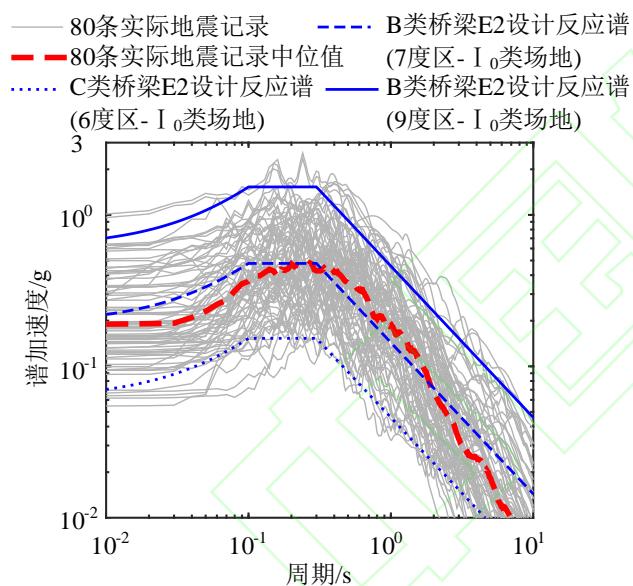
图 3 选用的 80 条地震记录加速度反应谱及其与我国规范中 \mathrm{I_0} 类场地设计反应谱的比较
Fig.2 Analysis framework for loss estimates of post-earthquake vertical load-carrying capacity of bridges
Fig.3 Spectral accelerations of adopted 80 ground motion records and their comparisons with design response spectra for type I _0 soil in Chinese Seismic Design Code
在 IDA 中的每一个时程分析结束后,对处于震后残余状态桥梁施加不断增加的竖向荷载,即进行 Pushdown 分析,此时桥梁能承受的最大竖向荷载即为震后竖向残余承载能力,记为 P_{r} 。值得一提的是,为了保证 Pushdown 分析在稳定的震后残余状态 (即不再振动的静止状态) 下进行,IDA 的时程分析中每条地震动后增加了 60s 零加速度值39;此外,以往的试验和理论研究表明10,18,60,液化土体的超孔隙水压往往会在震后很短的时间内消散。因此,本文不考虑土体液化 (即超孔隙水压的发展) 对桥梁震后竖向承载能力的影响。
为了分析地震引起的竖向承载能力损失,还需要获得桥梁在地震前的竖向承载能力。为此,重新建立数值模型,直接对无损伤状态的桥梁进行 Pushdown 分析,此时桥梁能承受的最大竖向荷载即为震前桥梁的竖向承载能力,记为 P 。桥梁竖向承载能力百分比损失 L_{\nu} 可作为桥梁震后通行决策的关键指标,按下式计算:
3 震后竖向承载能力损失机理
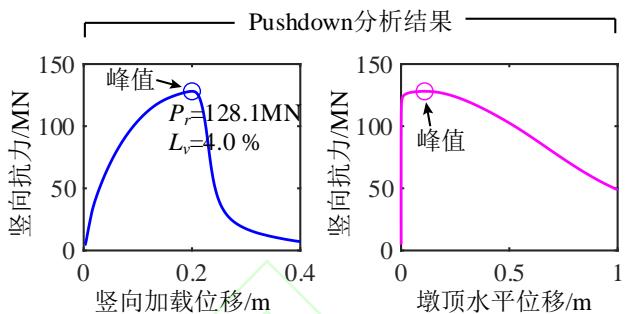
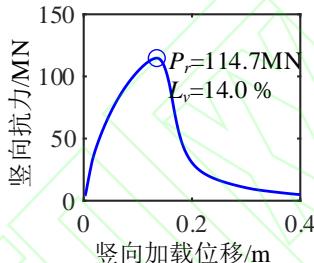
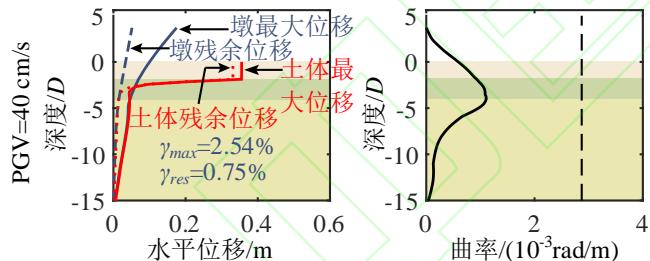
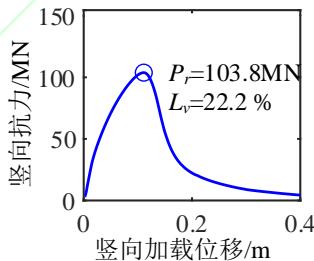
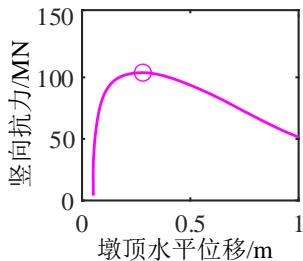
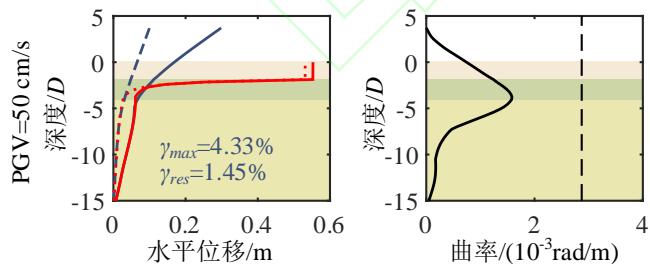
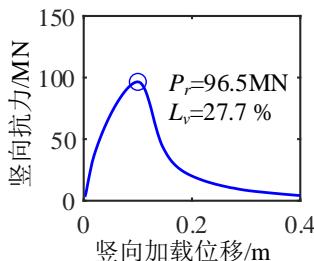
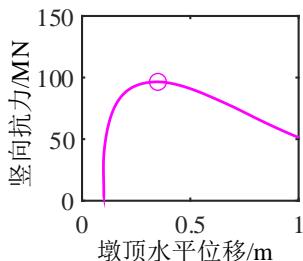
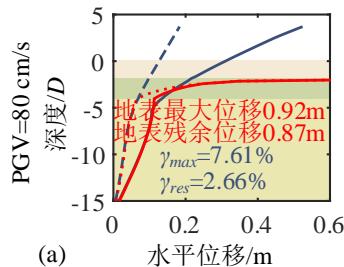
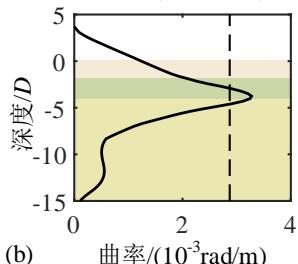
为了深入分析液化大变形场地桩柱式墩桥梁震后竖向承载能力损失的机理,图 4 给出了一个典型代表工况的完整计算结果。该工况墩柱的直径为 1.86\mathrm{m},墩高 6.9\mathrm{m},轴压比 5.3\%,纵筋配筋率 2\%,配箍率 0.52\%;钢筋屈服强度、弹性模量和硬化率分别是 430.7\mathrm{MPa}、202.4\mathrm{GPa} 和 0.0146;保护层混凝土抗压强度、抗压强度对应的应变和极限应变分别是 36.3\mathrm{MPa}、0.003 和 0.0063;核心混凝土抗压强度、抗压强度对应的应变和极限应变分别是 43.6\mathrm{MPa}、0.0061 和 0.0176;土面倾角 1.7^\circ,上覆粘土层厚 3\mathrm{m},不排水剪切强度 37.5\mathrm{kPa};可液化砂土层厚 4\mathrm{m},相对密实度 53.9\%。地震动输入为 Loma Prieta 地震记录 (NGA 数据库的 RSN 编号61为 769)。图 4 中至上而下分别给出了 PGV 为 5\mathrm{cm/s} 、 10\mathrm{cm/s} 、 30\mathrm{cm/s} 、 40\mathrm{cm/s} 、 50\mathrm{cm/s} 以及 80\mathrm{cm/s} 的结果,从左到右依次为桩柱式墩及土体地震位移包络,桩柱式墩地震曲率包络,Pushdown 曲线 (竖向力 - 位移曲线),以及竖向加载过程中墩顶水平位移的发展曲线。
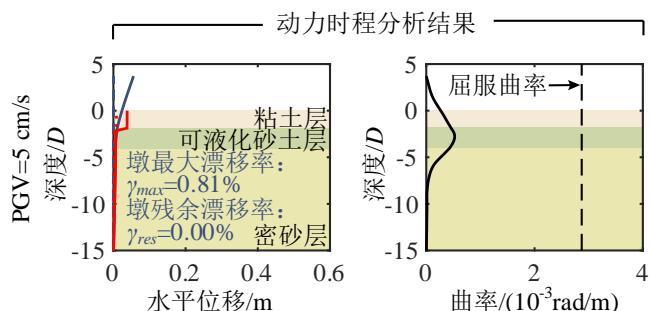
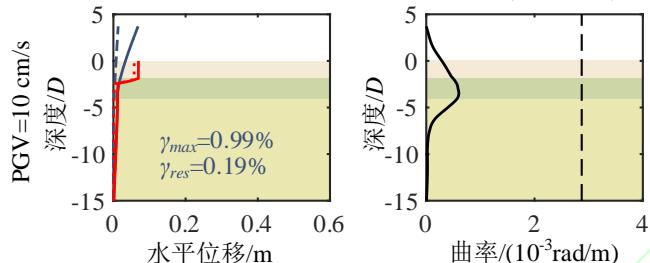
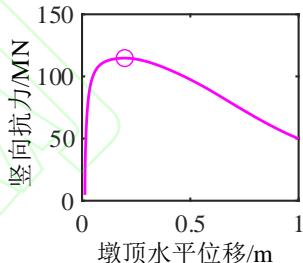
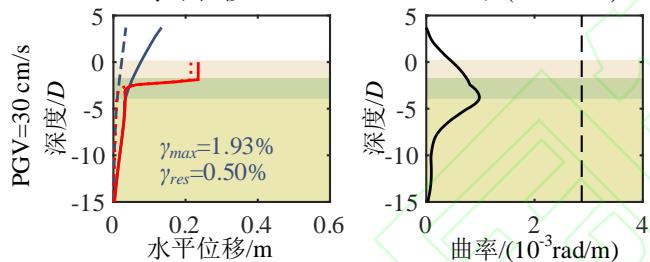
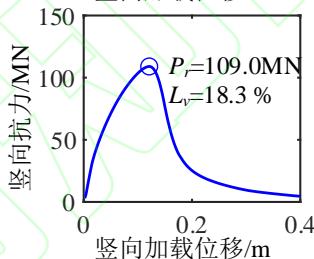
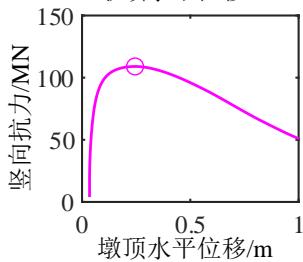
(a) 地震位移包络分布
(b) 地震曲率包络分布
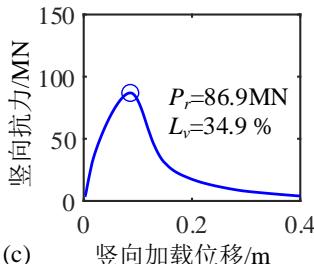
(c)Pushdown 曲线
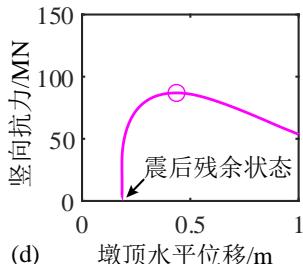
(d) 竖向加载时水平位移的发展
由图 4(a) 可知,随着地震动强度的增加,墩柱和土体的最大、残余变形均逐渐增大。当地震动强度较小时,土层侧扩位移较小,结构保持弹性,几乎没有残余变形。随着地震动强度的增长,液化侧扩现象开始出现,即上覆粘土层的残余变形迅速增加,导致墩柱的残余变形迅速增加,逐渐达到了最大变形的三分之一。当 PGV 为 80\mathrm{cm/s} 时,地表的最大、残余位移分别高达 0.92\mathrm{m} 和 0.87\mathrm{m} (超出了图 4(a) 的水平轴范围,未画出 ),墩柱的最大、残余漂移率分别高达 7.61\% 和 2.66\%。
震后墩柱截面钢筋、混凝土的损伤通过曲率分布表征。由图 4(b) 可知,墩柱的最大曲率发生在土下约 3.7 倍墩径处,接近松砂与密砂的分界线,这与以往现场震害调研62、室内试验研究63以及理论分析58的结论相符。尽管地震下桩柱式墩的侧向位移较大,但直到 PGV 达到 80\mathrm{cm/s} 、地表侧向滑移高达近 1\mathrm{m} 的情况下才屈服,即液化场地桩柱式墩的侧向变形主要由场地变形引起,而非桩柱截面本身的塑性损伤。
由图 4(c) 可知,桩柱式墩的竖向抗力随竖向位移荷载的增加而增大,在达到峰值后迅速下降。由图 4(d) 可知,在竖向加载的初期,墩柱的水平位移几乎不变,当竖向抗力接近峰值时墩柱的水平位移迅速增加。地震动越强,墩柱震后竖向承载能力越小,对应的墩柱竖向位移越小,水平位移越大。这是因为地震动越强,墩柱的震后残余变形越大,在竖向加载过程中 P-\Delta 效应越显著,墩柱的水平位移发展越快,P-\Delta 效应引起的弯矩越大,最终导致墩柱截面的抗压承载能力降低。此工况桥梁的震前竖向承载能力为 133.4\mathrm{MN},桥梁竖向承载能力的损失由 PGV 为 5\mathrm{cm/s} 时的 4\% 增长至 PGV 为 80\mathrm{cm/s} 时的 34.9\%。值得一提的是,只要支座与上、下部结构的连接可靠,传力路径稳定,其在竖向加载过程中变形很小,故可不考虑支座变形对桥梁竖向承载能力的影响。
为了进一步分析液化大变形场地桩柱式墩桥梁震后竖向承载能力损失的机理,图 5 给出了所有工况中震后墩柱残余漂移率与地表残余变形以及墩柱曲率延性系数之间的关系。其中曲率延性系数常用于墩柱塑性损伤等级划分,定义为截面的地震曲率需求除以等效屈服曲率 (通过对截面的弯矩 - 曲率关系曲线按能量进行双线性等效获得)。由图 5 可知,墩柱的残余漂移率与地表的残余位移在对数空间存在明显的线性相关性 ( 拟合优度 R^2 为 0.54,标准差 \beta 为 0.8),而根据以往研究中对墩柱损伤等级的划分64, 87\% 工况墩柱在震后处于无损伤或轻微损伤的状态。以上分析结果进一步验证了墩柱的残余变形主要是砂土液化诱发的上覆非液化土层大变形导致,墩柱的竖向承载能力损失应归因于震后残余变形下竖向加载引起的 P-\Delta 效应,而非墩柱截面本身的塑性损伤。
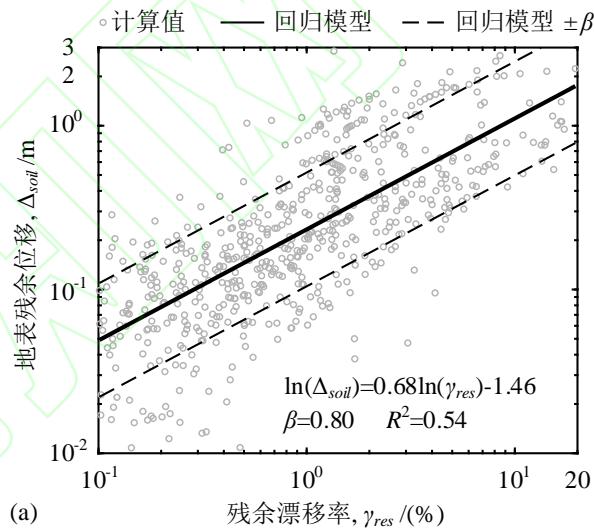
图 4 典型结果
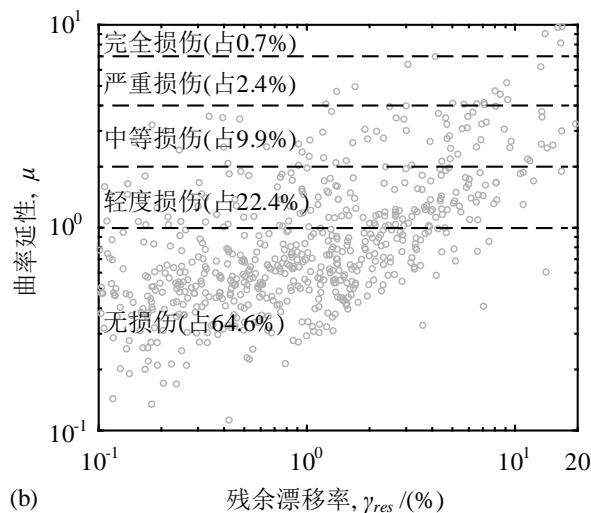
Fig.4 Indicative results
图 5 震后墩柱残余漂移率与 (a) 地表残余位移以及 (b) 墩柱曲率延性之间的关系
Fig.5 Relationships between the residual drift ratio of pile-column and the: (a) residual displacement of ground soil; (b) curvature ductility of pile-column
4 震后竖向承载能力损失评估模型
4.1 量化回归模型
相较于地震中桥墩的最大变形,桥墩震后的残余变形是更易测量的指标39。由上节可知,液化场地桩柱式墩桥梁的震后竖向承载能力与桥墩残余变形有着紧密联系。因此,可以通过建立两者的关联关系,根据震后桥墩残余漂移率,对竖向承载能力的损失进行快速评估。
在实际工程中,墩柱的残余漂移率低于 0.1\% 时很难准确测量,因此本文仅对残余漂移率大于 0.1\% 的工况的竖向承载能力损失进行统计分析。图 6 给出震后竖向承载能力的损失与墩柱残余漂移率之间的回归关系,如下式:
式中: \overline{L_{\nu}} 为给定桥墩残余漂移率 \gamma_{res} 下震后竖向承载能力损失的均值; \beta 为回归模型的标准差; L_{\nu i} 为第 i 个样本的桥梁震后竖向承载能力损失计算值,N 为计算样本数量。由式 (2) 可知,液化大变形场地桩柱式墩桥梁的震后竖向承载能力损失与桥墩的残余漂移率呈幂函数的关系。
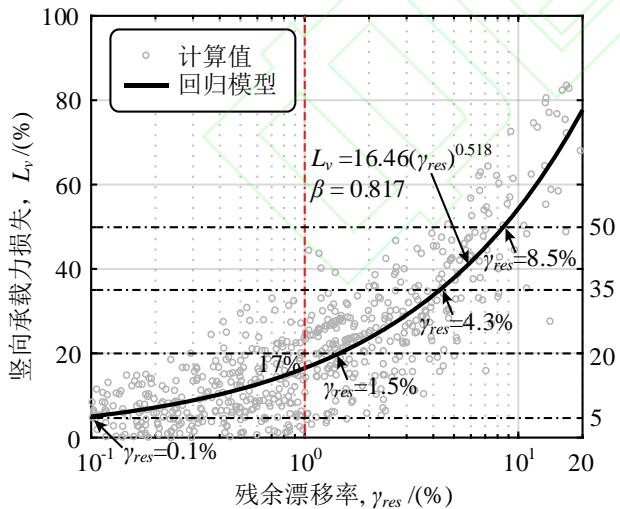
图 6 震后竖向承载能力损失量化回归模型
Fig.6 Regression models for estimating the loss of vertical load-carrying capacity after earthquake
Mackie 和 Stojadinović7推荐了美国加州高速公路跨线桥的限重通行、单车道通行、紧急通行、以及关闭状态对应的竖向承载能力损失阈值 L_{vc} 分别为 5\% 、 20\% 、 35\% 、以及 50\% 。尽管该阈值对我国桥梁的适用性有待商榷,但仍值得探究此阈值对应的桥墩残余漂移率。由式 (2) 的回归模型可得对应的平均残余漂移率分别为 0.1\% 、 1.5\% 、 4.3\% 以及 8.5\% ,可作为桩柱式墩多级性能指标,为桥梁震后竖向承载能力损失的快速评估提供依据。
1995 年日本阪神地震后,将残余漂移率超过 1.75\% 的桥墩进行拆除重建65,并在之后修订的桥梁抗震设计规范中偏保守地规定桥墩最大容许残余漂移率为 1\% 66。根据本文的回归模型 (图 6), 1\% 残余漂移率下,桥梁震后竖向承载能力损失的均值为 17\%,但离差较大, 1\% 残余漂移率附近的计算结果范围约为 2\% \sim 45\%。
4.2 概率评估模型
考虑到前述回归模型的离差较大,本文提出了基于概率的桥梁震后竖向承载能力损失评估模型。由于研究对象各参数的不确定性模型多数为正态或对数正态分布 (表 1),可合理地假定桥梁震后竖向承载能力损失满足对数正态分布。据此,结合条件概率和随机变量累积分布概率求解的相关理论67,可采用标准正态累积分布函数 (\Phi) 确定某一残余漂移率 \gamma_{res} 下桥梁的竖向承载能力损失 (L_{v}) 超过某一限值 (L_{vc}) 的条件概率:
图 7 给出了不同承载能力损失限值、不同残余漂移率下,桥梁震后承载能力损失的超越概率。可知,当桥墩的残余漂移率为日本规范规定的最大容许值 1\% 时,桥梁震后竖向承载能力损失超过 5\% 、 20\% 、 35\% 、以及 50\% 的概率分别为 93\% 、 41\% 、 18\% 、以及 9\% 。该概率评估模型可作为前述量化回归模型 (式(2)) 的补充,提供更可靠的评估结果。
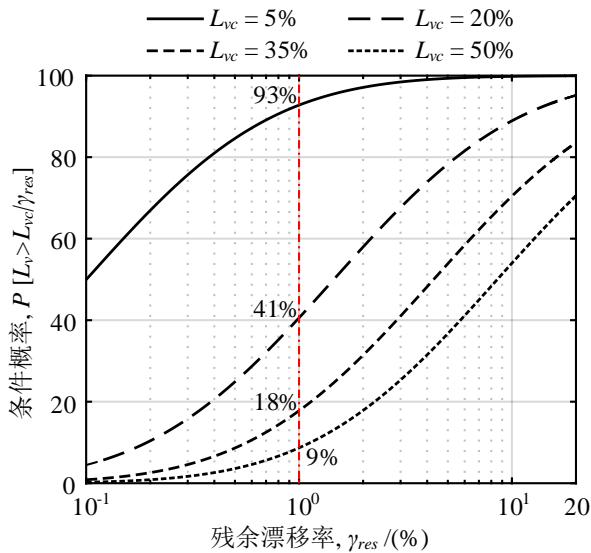
图 7 不同残余漂移率下震后竖向承载能力损失超越不同阈值的概率
Fig.7 Probability of vertical load-carrying capacity exceeding different thresholds given different residual drift ratios
5 结论
本文提出了一种基于 IDA 与 Pushdown 的桥梁震后竖向承载能力损失分析方法,并针对液化大变形场地桩柱式墩桥梁开展了承载能力损失评估研究,给出了基于桥墩残余漂移率的竖向承载能力损失量化回归模型和概率评估模型,并提出了面向震后竖向承载能力损失的桩柱式墩多级性能指标。主要结论如下:
(1) 桩柱式墩的震后残余变形主要由砂土液化诱发的上覆土层侧向大变形引起,而桩柱本身的塑性损伤次之。震后竖向承载能力损失的机理是桩柱残余变形加之竖向加载过程中的 P-\Delta 效应。
(2) 桩柱式墩桥梁的震后竖向承载能力损失与桥墩的残余漂移率呈幂函数关系;竖向承载能力损失 5\% 、 20\% 、 35\% 和 50\% 对应的残余漂移率分别为 0.1\% 、 1.5\% 、 4.3\% 和 8.5\% ,可作为面向震后承载能力评估的液化大变形场地桩柱式墩多级性能指标。
(3) 从概率上讲,当桥墩残余漂移率为日本规范规定的最大容许值 1\% 时,桥梁震后竖向承载能力损失超过 5\% 、 20\% 、 35\% 以及 50\% 的概率分别为 93\% 、 41\% 、 18\% 以及 9\% 。
须说明的是,本文主要从震后应急的角度探讨桥梁的竖向承载能力损失,结论主要基于所考虑的场地、结构、地震动强度参数范围,对于超过此范围的情况,应用时应特别注意,但相关结论仍有参考价值。
参考文献:
凌贤长, 唐亮. 液化侧扩流场地桥梁桩基抗震研究进展 [J]. 地震工程与工程振动, 2015, 35(1): 1-10. ↩
王晓伟, 李闯, 叶爱君, 等. 可液化河谷场地简支梁桥的地震反应分析 [J]. 中国公路学报, 2016, 29(4): 85-95. ↩
LIN S S, TSENG Y J, CHIANG C C, et al. Damage of piles caused by lateral spreading — back study of three cases[C]/Seismic Performance and Simulation of Pile Foundations in Liquefied and Laterally Spreading Ground. Reston, VA: American Society of Civil Engineers, 2005: 121-133. ↩
BHATTACHARYA S, TOKIMATSU K, GODA K, et al. Collapse of Showa Bridge during 1964 Niigata earthquake: A quantitative reappraisal on the failure mechanisms[J]. Soil Dynamics and Earthquake Engineering, 2014, 65: 55-71. ↩
陈志雄, 李康银, 王成龙, 等. 液化侧向扩展场地刚性排水管桩群桩振动台试验研究 [J]. 工程力学, 2022, 39(9): 141-152. ↩
张鑫磊, 衣睿博, 纪展鹏, 等. 循环荷载作用下饱和砂土的性质演化规律及液化阶段性特征 [J]. 工程力学, 2023, 40(2): 157-167. ↩
MACKIE K R, STOJADINOVIĆ B. Post-earthquake functionality of highway overpass bridges[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(1): 77-93. ↩ ↩ ↩
O'CONNOR J S. Post-earthquake bridge inspection guidelines[R]. Buffalo, NY: Multidisciplinary Center for Earthquake Engineering Research, SUNY University at Buffalo, 2010: C-06-14. ↩
HUTCHINSON T C, CHAI Y H, BOULANGER R W, et al. Inelastic seismic response of extended pile-shaft-supported bridge structures[J]. Earthquake Spectra, 2004, 20(4): 1057-1080. ↩
BRANDENBERG S J, BOULANGER R W, KUTTER B L, et al. Behavior of pile foundations in laterally spreading ground during centrifuge tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(11): 1378-1391. ↩ ↩
王睿, 张建民, 张嘎. 侧向流动地基单桩基础离心机振动台试验研究 [J]. 工程力学, 2012, 29(10): 98-105. ↩
ZHANG S, WEI Y, CHENG X, et al. Centrifuge modeling of batter pile foundations in laterally spreading soil[J]. Soil Dynamics and Earthquake Engineering, 2020, 135: 106166. ↩
李雨润, 闫志晓, 张健, 等. 饱和砂土中直群桩动力响应离心机振动台试验与简化数值模型研究 [J]. 岩石力学与工程学报, 2020, 39(6): 1252-1264. ↩
凌贤长, 王东升. 液化场地桩 - 土 - 桥梁结构动力相互作用振动台试验研究进展 [J]. 地震工程与工程振动, 2002, 22(4): 53-59. ↩
徐鹏举, 胡庆立, 凌贤长. 液化场地单桩 - 土 - 桥梁结构地震相互作用大型振动台试验研究 [J]. 土木工程学报, 2010, 43(S2): 327-332. ↩
张鑫磊, 王志华, 许振巍, 等. 土体液化大位移条件下群桩动力反应振动台模型试验 [J]. 工程力学, 2016, 33(5): 150-156. ↩
EBEIDO A, ELGAMAL A, TOKIMATSU K, et al. Pile and pile-group response to liquefaction-induced lateral spreading in four large-scale shake-table experiments[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(10): 04019080. ↩
WANG X, YE A, SHANG Y, et al. Shake-table investigation of scoured RC pile-group-supported bridges in liquefiable and nonliquefiable soils[J]. Earthquake Engineering & Structural Dynamics, 2019, 48(11): 1217-1237. ↩ ↩
苏雷, 唐亮, 凌贤长, 等. 液化侧扩流场地桩基动力反应振动台试验数值模拟 [J]. 防灾减灾工程学报, 2019, 39(2): 227-235. ↩
徐丹, 杜春波, 王涛. 可液化场地高桩桥梁振动台模型试验研究 [J]. 工程力学, 2020, 37(S): 168-171. ↩
贾科敏, 许成顺, 杜修力, 等. 液化侧向扩展场地 - 群桩基础 - 结构体系地震破坏反应大型振动台试验方案设计 [J]. 工程力学. doi:10.6052/j.issn.1000-4750.2021.11.0922 ↩
WANG X, JI B, YE A. Seismic behavior of pile-group-supported bridges in liquefiable soils with crusts subjected to potential scour: Insights from shake-table tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(5): 04020030. ↩
MOHANTY P, XU D, BISWAL S, et al. A shake table investigation of dynamic behavior of pile supported bridges in liquefiable soil deposits[J]. Earthquake Engineering and Engineering Vibration, 2021, 20(1): 1-24. ↩
JIA K, XU C, EL NAGGAR M H, et al. Large-scale shake table testing of pile group-bridge model in inclined liquefiable soils with overlying crusts[J]. Soil Dynamics and Earthquake Engineering, 2022, 163: 107555. ↩
ZHANG J, HUTCHINSON T C. Inelastic pile behavior with and without liquefaction effects[J]. Soil Dynamics and Earthquake Engineering, 2012, 36: 12-19. ↩
KHOSRAVIFAR A, BOULANGER R W, KUNNATH S K. Effects of liquefaction on inelastic demands on extended pile shafts[J]. Earthquake Spectra, 2014, 30(4): 1749-1773. ↩ ↩
王晓伟, 叶爱君, 罗富元. 液化场地桩柱式基础桥梁结构地震反应的敏感性分析 [J]. 工程力学, 2016, 33(8): 132-140. ↩
李钟雄, 徐略勤, 李建中. 砂土液化分析方法对连续梁桥地震响应的影响对比研究 [J]. 结构工程师, 2017, 33(3): 88-96. ↩
王晓伟, 叶爱君, 李闯. 可液化河谷场地不同形式梁式桥的地震反应 [J]. 同济大学学报 (自然科学版), 2018, 46(6): 759-766. ↩
QIU Z, LU J, EBEIDO A, et al. Bridge in narrow waterway: seismic response and liquefaction-induced deformations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2022, 148(8): 04022064. ↩
古泉, 俞至权, 邱志坚. 考虑碎石桩加固的液化场地桥梁地震风险分析 [J]. 湖南大学学报(自然科学版), 2022, 49(7): 178-185. ↩
董召先, 孙治国, 李宏男, 等. 液化场地钢筋混凝土桥墩残余位移分析 [J]. 工程力学. doi: 10.6052/j.issn.1000-4750.2022.01.0083 ↩
WANG X, LUO F, YE A. A holistic framework for seismic analysis of extended pile-shaft-supported bridges against different extents of liquefaction and lateral spreading[J]. Soil Dynamics and Earthquake Engineering, 2023, 170: 107914. ↩
QIU Z, YU Z, SU L, et al. Longitudinal seismic fragility assessment of an integral bridge-ground system in liquefaction-induced lateral spreads[J]. Soil Dynamics and Earthquake Engineering, 2023, 168: 107838. ↩
ARDAKANI S M S, SAIDI M S. Design of reinforced concrete bridge columns for near-fault earthquakes[R]. Reno, NV: University of Nevada, Reno, 2013: CCEER 13-13. ↩
TERZIC V, STOJADINOVIC B. Evaluation of post-earthquake axial load capacity of circular bridge columns[J]. ACI Structural Journal, 2015, 112(1): 23-34. ↩
ZHOU L, YE A, CHEN F. Postearthquake vertical load-carrying capacity of extended pile shafts in cohesionless soils: quasi-static test and parametric studies[J]. Journal of Bridge Engineering, 2022, 27(8): 04022071. ↩
ZHOU L, BARBATO M, YE A. Experimental investigation of postearthquake vertical load-carrying capacity of scoured reinforced concrete pile group bridge foundations[J]. Journal of Bridge Engineering, 2021, 26(12): 04021091. ↩
WANG X, SHAFIEEZADEH A, YE A. Optimal EDPs for post-earthquake damage assessment of extended pile-shaft-supported bridges subjected to transverse spreading[J]. Earthquake Spectra, 2019, 35(3): 1367-1396. ↩ ↩ ↩
MCKENNA F. OpenSees: A framework for earthquake engineering simulation[J]. Computing in Science & Engineering, 2011, 13(4): 58-66. ↩ ↩
WANG X, LUO F, SU Z, et al. Efficient finite-element model for seismic response estimation of piles and soils in liquefied and laterally spreading ground considering shear localization[J]. International Journal of Geomechanics, 2017, 17(6): 06016039. ↩ ↩ ↩
MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826. ↩
高健峰, 李建中, 梁博. 考虑粘结滑移效应的墩柱低周往复加载模拟方法 [J]. 工程力学, 2023, 40(2): 74-84. ↩
AASHTO, LRFD bridge design specifications[S]. Washington, DC: American Association of State Highway and Transportation Officials, 2020. ↩
JONES A L, KRAMER S L, ARDUINO P. Estimation of uncertainty in geotechnical properties for performance-based earthquake engineering [R]. Berkeley, CA: Pacific Earthquake Engineering Research Center, 2002. ↩ ↩
WANG X. Empirical probability distribution models for soil-layer thicknesses of liquefiable ground[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147(6): 06021005. ↩ ↩
GRANT A, WARTMAN J, ABOU-JAOUDE G. Multimodal method for coseismic landslide hazard assessment[J]. Engineering Geology, 2016, 212: 146-160. ↩
WANG X, YE A, JI B. Fragility-based sensitivity analysis on the seismic performance of pile-group-supported bridges in liquefiable ground undergoing scour potentials[J]. Engineering Structures, 2019, 198: 109427. ↩
BRANDENBERG S J, KASHIGHANDI P, ZHANG J, et al. Fragility functions for bridges in liquefaction-induced lateral spreads[J]. Earthquake Spectra, 2011, 27(3): 683-717. ↩ ↩ ↩
PANG Y, WU X, SHEN G, et al. Seismic fragility analysis of cable-stayed bridges considering different sources of uncertainties[J]. Journal of Bridge Engineering, 2014, 19(4): 04013015. ↩
BARBATO M, GU Q, CONTE J P. Probabilistic push-over analysis of structural and soil-structure systems[J]. Journal of Structural Engineering, 2010, 136(11): 1330-1341. ↩ ↩ ↩ ↩ ↩
CELAREC D, DOLŠEK M. The impact of modelling uncertainties on the seismic performance assessment of reinforced concrete frame buildings[J]. Engineering Structures, 2013, 52: 340-354. ↩
VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491-514. ↩
BAKER J W, LIN T, SHAHI S K, et al. New ground motion selection procedures and selected motions for the PEER transportation research program[R]. Berkeley, CA: Pacific Earthquake Engineering Research Center, 2011. ↩
JTG/T 2231-01—2020, 公路桥梁抗震设计规范 [S]. 北京: 人民交通出版社, 2020. ↩
WANG Z, DUEÑAS-OSORIO L, PADGETT J E. Optimal intensity measures for probabilistic seismic response analysis of bridges on liquefiable and non-liquefiable soils[C]//Structures Congress 2012. Reston, VA: American Society of Civil Engineers, 2012: 527-538. ↩
WANG X, SHAFIEEZADEH A, YE A. Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground[J]. Bulletin of Earthquake Engineering, 2018, 16: 229-257. ↩
WANG X, SHAFIEEZADEH A, PADGETT J E. FOSID: a fractional order spectrum intensity for probabilistic seismic demand modeling of extended pile-shaft-supported highway bridges under liquefaction and transverse spreading[J]. Bulletin of Earthquake Engineering, 2021, 19: 2531-2559. ↩ ↩
SUZUKI A, IERVOLINO I. Italian vs. worldwide history of largest PGA and PGV[J]. Annals of Geophysics, 2017, 60(5): S0511. ↩
HA I S, PARK Y H, KIM M M. Dissipation pattern of excess pore pressure after liquefaction in saturated sand deposits[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003, 1821: 59-67. ↩
POWER M, CHIOU B, ABRAHAMSON N, et al. An overview of the NGA project[J]. Earthquake Spectra, 2008, 24(1): 3-21. ↩
ARULMOLI K, MARTIN G, GASPARRO M, et al. Design of pile foundations for liquefaction-induced lateral spread displacements[C]//Geotechnical Engineering for Transportation Projects. Reston, VA: ASCE, 2004: 1673-1681. ↩
BRANDENBERG S J. Behavior of pile foundations in liquefied and laterally spreading ground[D]. Davis, California: Ph.D. dissertation, University of California, Davis, 2005. ↩
CHOI E, DESROCHES R, NIELSON B. Seismic fragility of typical bridges in moderate seismic zones[J]. Engineering Structures, 2004, 26(2): 187-199. ↩
KAWASHIMA K, MACRAE G A, HOSHIKUMA J, et al. Residual displacement response spectrum[J]. Journal of Structural Engineering, 1998, 124(5): 523-530. ↩
JRA, Specifications for highway bridges, Part V Seismic design[S]. Tokyo: Japan Road Association, 2002. ↩
ANG A H, TANG W H. Probability concepts in engineering: Emphasis on applications to civil and environmental engineering[M]. Hoboken, NJ: Wiley, 2006. ↩