Xiaowei Wang, Aff.M.ASCE^1; and Aijun Ye^2
^1 Assistant Professor, Dept. of Civil Engineering, Hohai Univ., 1 Xikang Rd., Nanjing 210024, China. E-mail: x.wang@hhu.edu.cn
^2 Professor, State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji Univ., 1239 Siping Rd., Shanghai 200092, China. E-mail: yeaijun@tongji.edu.cn
ABSTRACT
Characterizing the effect of varying design parameters on the seismic performance of bridges can assist in optimum seismic design, especially for those in complex geotechnical conditions where scour and liquefaction hazards occur. This paper presents results of sensitivity analyses on the seismic performance of pile-group-supported bridges under combined effects of scour and liquefaction hazards. A fragility-based tornado diagram method is proposed for the sensitivity analyses. The studied parameters include the column height, diameter and axial compressive ratio, pile diameter and center-to-center distance, and relative densities of loose and dense sands. Special attention is paid to the influence of scour depth on the sensitivity-ranking of the parameters. Main findings are that the pile diameter and center-to-center distance show increasing sensitivity with the increase of scour depth. These two parameters should be treated carefully in the seismic design of scoured bridges in liquefaction ground. On the contrary, relative densities of loose and dense sands that show significant influences for the scenario without scour turn to be the least sensitive parameters for scoured scenarios.
INTRODUCTION
Scour is reported to be one of the most severe hazards causing river-crossing bridge failures in the United States 8. Fig. 1 shows a typical river-crossing multi-span bridge that was subjected to scour hazard. The upper portion of the pile-group foundation was exposed without surrounding soils due to scour. Meanwhile, saturated sands in scoured bridge sites may liquefy under strong earthquakes. Soil liquefaction-induced damage to piles and associated failure of bridges have been witnessed in several historical earthquakes 3. Previous studies, regardless of experiments or numerical analyses, on the seismic performance of bridges always considered the effect of liquefaction or scour separately 4,15,19. However, in practice, it is a common scenario that bridges are located in flood-induced scour sites where the saturated sands may liquefy under earthquakes. The prediction of seismic performance of bridges in such complex geotechnical conditions requires special attention for both engineers and academic scholars.
Numerical predictions on the seismic performance of soil-bridge systems may be susceptible to varied design parameters. From a predictive point of view, it is desirable to characterize impacts of these parameters, which can assist in optimum seismic design of bridges. Using parametric or sensitivity analyses, previous studies mainly quantify these impacts on the seismic response or performance of bridges in scour or liquefiable conditions, separately 5,10,14,16. To the best knowledge of the authors, sensitivity analyses on the seismic performance of bridges under combined effects of scour and liquefaction hazards are not well documented, let alone the impact of scour depth on sensitivities of the design parameters. These issues provide the motivation for the present study.

This study performs sensitivity analyses to identify bridge design parameters that have the most and least significant effects on the seismic performance of bridges under combined effects of scour and liquefaction hazards. A fragility-based Tornado diagram method for the sensitivity analyses is introduced first. Then, coupled soil-bridge finite element (FE) models are built, which represent typical multi-span reinforced concrete bridges supported by pile-group foundations in scoured ground that may undergo liquefaction under earthquakes. Real site unscaled ground motions are selected for probabilistic seismic demand analyses, which are used to generate fragility curves. Finally, sensitivity results are discussed to provide insights into the seismic design of bridges under combined effects of scour and liquefaction.
PROPOSED METHOD FOR SENSITIVITY ANALYSES
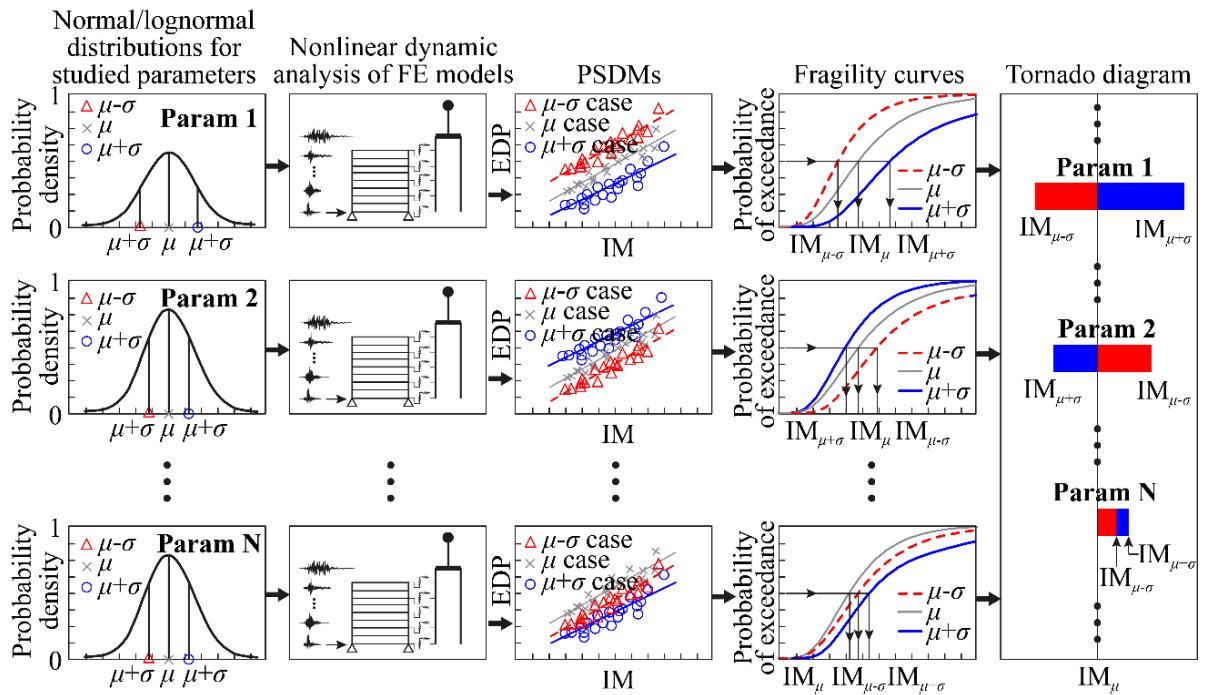
There are several techniques for sensitivity analyses, mainly including Tornado diagram, First-Order Second-Moment, and Monte Carlo simulation. Among them, the Monte Carlo simulation often requires heavy computational efforts, especially for this study where complex soil-foundation-structure interactions are involved for the nonlinear dynamic analyses. By comparison, Tornado diagram is an efficient solution from a practical view. On the other hand, this study concentrates on the seismic performance assessment, rather than the seismic response merely. Hence, fragility analyses are used to rigorously estimate the seismic performance of bridges. In addition, fragility analyses can efficiently reveal the performance at multi-level damage states. Considering these merits, a fragility-based Tornado diagram method is proposed in the present study for the sensitivity analyses. Fig. 2 illustrates the main process of this method, which is further described as follows.
For a parameter supposing a normal or lognormal distribution, two extreme values at 16th and 84th percentiles (i.e., mean, \mu, minus and plus standard deviation, \sigma)are adopted as lower and upper bounds, respectively. A set of ground motions is used for dynamic analyses of three FE models where parameters with the lower, mean, and upper values are involved, respectively. Probabilistic seismic demand analyses are performed to establish the corresponding three probabilistic seismic demand models (PSDMs). Accordingly, based on the mathematical basis for fragility curves 7, as well as the established PSDMs and pre-defined probabilistic capacity models, three fragility curves that reflect the impact of this parameter on the seismic performance of the bridges are generated using Eq. (1):
where \Phi(\cdot) is the standard normal cumulative distribution function, D is the demand, C is the capacity, S_D and S_C are median values of the demand and capacity, respectively, \beta_D and \beta_C are logarithmic standard deviations of the demand and capacity, respectively. Based on the fragility curves, intensity measure values at a given level of probability of exceedance (e.g., P_r = 50\%, the so-called median fragility values) are obtained as "performance indices" (i.e., IM_{\mu-\sigma}, IM_{\mu}, and IM_{\mu+\sigma}, as shown in Fig. 2) for this parameter in the Tornado diagram. Note that blue bars in the Tornado diagram indicate IM_{\mu+\sigma} while red bars represent IM_{\mu-\sigma}. Bars on the right side of the Tornado diagram represent cases with lower P_r. Repeating the above process for every studied design parameter, the obtained performance indices are sorted based on their ranges (from high to low) to fulfill the Tornado diagram. It is worth noting that for some parameters, the fragility curve derived from the model with the mean value (\mu) may not lie between the upper (\mu+\sigma) and lower (\mu-\sigma)values-based fragility curves. In this regard, the "ranges of performance indices" are defined using Eq. (2):
where |\cdot| is the absolute value operator.
NUMERICAL MODELS
A coupled multi-scale soil-bridge FE model is built in the OpenSees platform 11. Fig. 3 shows the schematic illustration of the FE model. A two-dimensional plane-strain soil model is linked to a three-dimensional simplified pile-group-supported bridge model using Winkler-foundation-based p\text{-}y, t\text{-}z, and q\text{-}z springs. This simplified multi-scale modelling technique has been validated by the authors 17 using three centrifuge tests in the literature. Elastic rubber bearings (ERBs) are used to connect the single column with the lumped mass that represents the superstructure. Abutments are not considered in this study. More specifically, each bent consists of a single column supported by a commonly used 3 \times 2 pile-group foundation embedded into saturated sands (loose sand overlying dense sand) that may undergo scour and earthquake-induced liquefaction hazards.
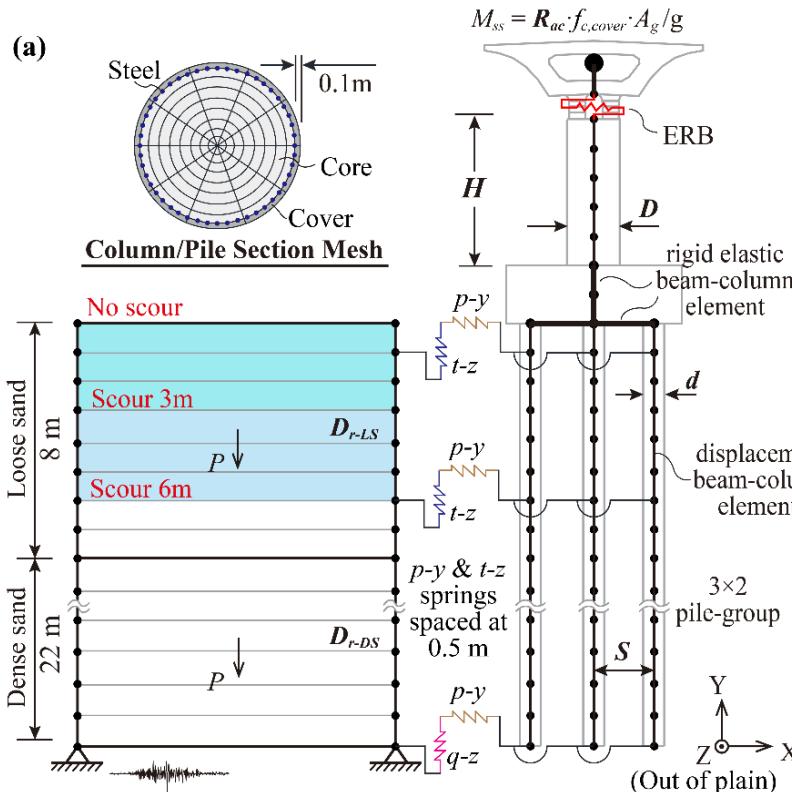
To assess the impact of scour depth on the sensitivity of seismic performance to design parameters, three scenarios are considered: 0\text{m} ("no scour"), 3\text{m}, and 6\text{m} (Fig. 3(a)). Table 1 lists the studied seven parameters that are assumed to follow normal distributions.
Table 1. Studied design parameters and their normal distribution properties
| Parameters | Notation (Unit) | Mean | COV | Lower | Upper |
|---|---|---|---|---|---|
| Column-related | |||||
| Height | H (m) | 6.5 | 0.26^a | 4.8 | 8.2 |
| Diameter | D (m) | 2 | 0.10^b | 1.8 | 2.2 |
| Axial compressive ratio | R_{ac} | 10% | 0.20^b | 8% | 12% |
| Pile-related | |||||
| Diameter | d (m) | 1 | 0.10^b | 0.90 | 1.10 |
| Center-to-center distance | S (m) | 3d | 0.15^b | 2.5d | 3.5d |
| Soil-related | |||||
| Loose sand relative density | D_{r-LS} | 0.37 | 0.19^c | 0.30 | 0.44 |
| Dense sand relative density | D_{r-DS} | 0.75 | 0.19^c | 0.61 | 0.89 |
^a 6; ^b Assumed based on engineering judgment; ^c 9.
The column axial compressive ratio (R_{ac})is defined using Eq. (3):
where M_{ss} is the superstructure mass, g is gravity, f_{c,\text{cover}} is the peak strength of concrete cover, and A_g is the gross area of the section.
The PDMY constitutive model in OpenSees 11 is used to model the saturated sands. p\text{-}y and t\text{-}z springs are spaced at 0.5\text{m} consistent with the soil element mesh. Group efficiency factors of 0.7, 0.8, and 0.9 are selected for S = 2.5d, 3d, and 3.5d, respectively 12.
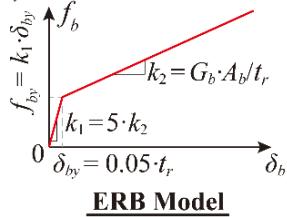
The 3 \times 2 piles and single column are modeled using displacement-based beam-column elements with fiber sections. Concrete fibers use the Concrete04 material (Table 2), and steel fibers use the Steel02 material (Table 3). The ERBs are modeled using a bilinear relationship 21, with G_b = 1200\text{kN/m}, t_r = 0.07\text{m}, and A_b following AASHTO 1.
Table 2. Model input variables of the Concrete04 material for concrete
| Component | f_{c,\text{cover}} (MPa) | \epsilon_{c,\text{cover}} | \epsilon_{cu,\text{cover}} | f_{c,\text{core}} (MPa) | \epsilon_{c,\text{core}} | \epsilon_{cu,\text{core}} |
|---|---|---|---|---|---|---|
| Column | 34 | 0.002 | 0.005 | 40.58 | 0.0039 | 0.0147 |
| Pile | 34 | 0.002 | 0.005 | 39.20 | 0.0035 | 0.0132 |
Table 3. Model input variables of the Steel02 material for rebars
| f_y (MPa) | E_s (GPa) | b | R_0 | CR_1 | CR_2 | a_1 | a_2 | a_3 | a_4 |
|---|---|---|---|---|---|---|---|---|---|
| 400 | 200 | 0.01 | 20 | 0.925 | 0.15 | 0 | 1 | 0 | 1 |
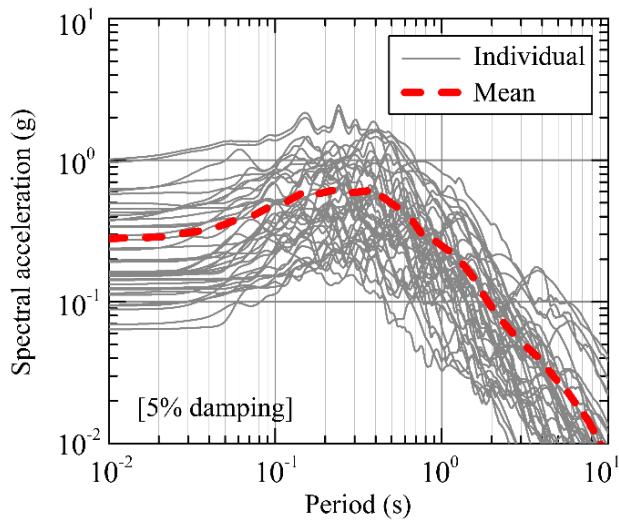
Forty real site unscaled ground motions 2 are adopted for each case. Fig. 4 shows the acceleration spectra. A total of 40 \times 15 = 600 dynamic analyses were performed.
Three engineering demand parameters (EDPs) are considered: bearing deformation, peak column curvature, and peak pile curvature (Table 4).
Table 4. Capacity values and dispersions for EDPs at slight damage states
| EDP | Unit | Capacity | Dispersion |
|---|---|---|---|
| Bearing deformation | m | 0.07 | 0.25^a |
| Column curvature | 1/m | 1.714 \times 10^{-3 \dagger} | 0.59^b |
| Pile curvature | 1/m | 3.556 \times 10^{-3 \dagger} | 0.59^b |
^a 14; ^b 13; ^\dagger Base case values.
RESULTS AND DISCUSSION
Fig. 5 displays the impact of scour depth on fragility curves for the base case. S_{a-2.0} (spectral acceleration at 2.0\text{s}) is adopted as the IM 18.
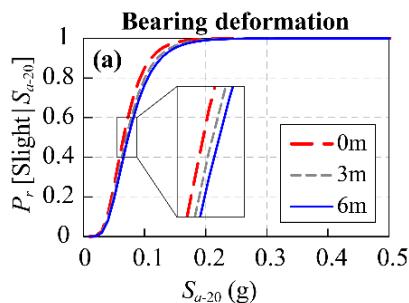
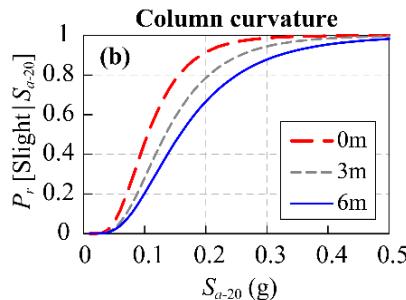
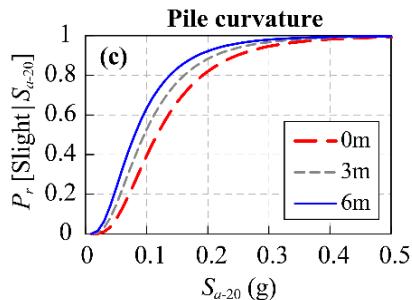
Scour depth has a minor impact on bearing performance but significant impacts on column and pile curvatures. The probability of exceedance (P_r)for column curvature decreases with scour depth (Fig. 5(b)) due to the isolation effect from elongated periods. Conversely, P_r for pile curvature increases with scour depth (Fig. 5(c)), indicating that scour transfers damage from columns to piles. This is consistent with studies on nonliquefiable ground 20.
Figs. 6 to 8 show Tornado diagrams for sensitivity-ranking. For bearing deformation (Fig. 6), R_{ac} and H are the most sensitive. Relative densities (D_{r-LS} and D_{r-DS})are sensitive without scour but least sensitive for scoured scenarios. For column curvature (Fig. 7), H and D are most sensitive. For pile curvature (Fig. 8), D_{r-LS} and D_{r-DS} dominate without scour, but pile-related parameters (d and S) show increasing sensitivity with scour depth.
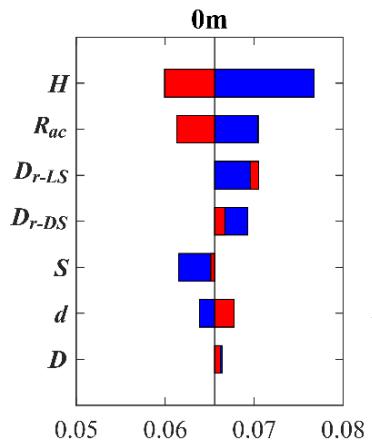
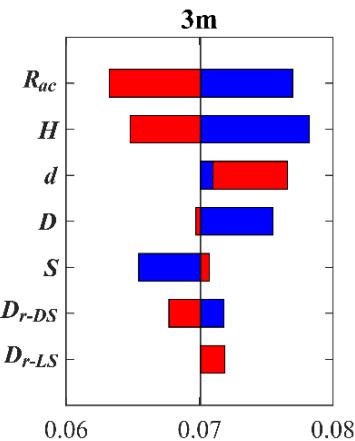
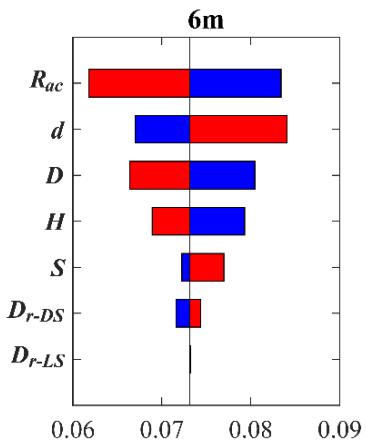
Fig. 6 Impact of scour depth (0 m, 3 m, 6 m) on Tornado diagram for bearing curvature
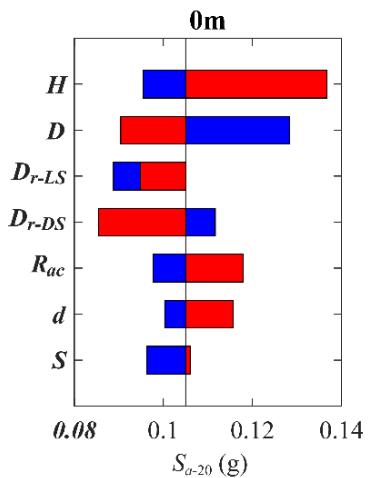
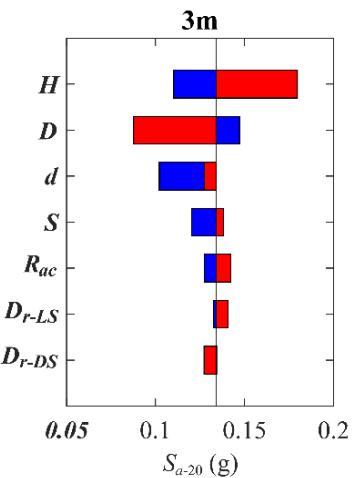
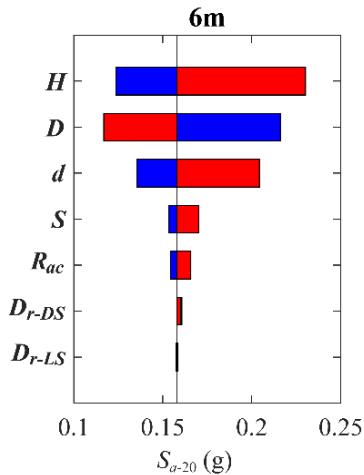
Fig. 7 Impact of scour depth (0 m, 3 m, 6 m) on Tornado diagram for column curvature
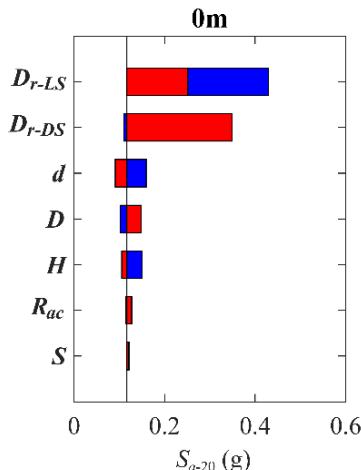
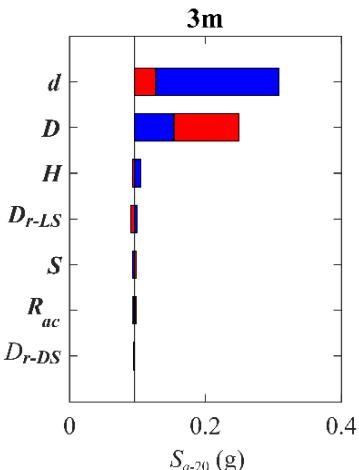
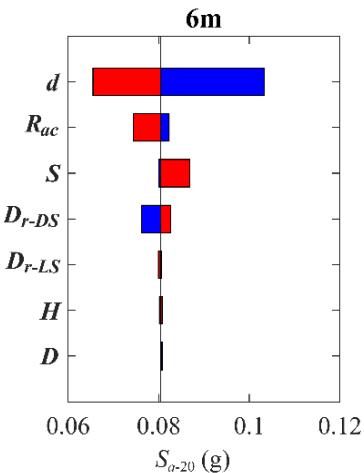
Fig. 8 Impact of scour depth (0 m, 3 m, 6 m) on Tornado diagram for pile curvature
SUMMARY AND CONCLUSIONS
This paper investigates the sensitivity of seismic performance of bridges under combined effects of scour and liquefaction. A fragility-based Tornado diagram method is proposed. It is found that R_{ac} and H are most sensitive for bearing performance. For column performance, D and H have the most significant effects. Pile-related parameters (d and S) show increasing sensitivity with scour depth, particularly for pile performance. Conversely, soil relative densities (D_{r-LS} and D_{r-DS}) are sensitive only for the no-scour scenario.
ACKNOWLEDGMENT
This work is supported by the National Nature Science Foundation of China (51778469) and the China Postdoctoral Science Foundation.
REFERENCES
AASHTO. AASHTO LRFD bridge design specifications. American Association of State Highway and Transportation Officials (AASHTO), Washington, D.C.; 2012. ↩
Baker J, Lin T, Shahi S, Jayaram N. New ground motion selection procedures and selected motions for the PEER transportation research program. Pacific Earthquake Engineering Research Center, Berkeley, CA; 2011. ↩
Bhattacharya S, Tokimitsu K, Goda K, Sarkar R, Shadlou M, Rouholamin M. "Collapse of Showa bridge during 1964 Niigata earthquake: A quantitative reappraisal on the failure mechanisms." Soil Dynamics and Earthquake Engineering, 65, 55-71; 2014. ↩
Brandenberg SJ, Boulanger RW, Kutter B, Chang D. "Behavior of pile foundations in laterally spreading ground during centrifuge tests." Journal of Geotechnical and Geoenvironmental Engineering, 131(11), 1378-1391; 2005. ↩
Brandenberg S, Kashighandi P, Zhang J, Huo Y, Zhao M. "Sensitivity study of an Older-Vintage Bridge subjected to lateral spreading." Geotechnical Earthquake Engineering and Soil Dynamics IV, ASCE, Reston, VA; 2008. ↩
Brandenberg S, Kashighandi P, Zhang J, Huo Y, Zhao M. "Fragility functions for bridges in liquefaction-induced lateral spreads." Earthquake Spectra, 27(3), 683-717; 2011. ↩
Cornell CA, Jalayer F, Hamburger R, Foutch D. "Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines." Journal of Structural Engineering, 128(4), 526-533; 2002. ↩
Deng L, Wang W, Yu Y. "State-of-the-art review on the causes and mechanisms of bridge collapse." Journal of Performance of Constructed Facilities, 30(2), 04015005; 2016. ↩
Jones A, Kramer S, Arduino P. Estimation of uncertainty in geotechnical properties for performance-based earthquake engineering. PEER Report, Pacific Earthquake Engineering Research Center, Berkeley, CA; 2002. ↩
Klinga J, Alipour A. "Assessment of structural integrity of bridges under extreme scour conditions." Engineering Structures, 82, 55-71; 2015. ↩
McKenna F. "OpenSees: A framework for earthquake engineering simulation." Computing in Science and Engineering, 13(4), 58-66; 2011. ↩ ↩
Mokwa R. "Investigation of the resistance of pile caps to lateral loading." Ph.D. dissertation, Virginia Tech, Blacksburg, VA; 1999. ↩
Nielson B, DesRoches R. "Analytical seismic fragility curves for typical bridges in the central and southeastern United States." Earthquake Spectra, 23(3), 615-633; 2007. ↩
Padgett J, Ghosh J, Dueñas-Osorio L. "Effects of liquefiable soil and bridge modelling parameters on the seismic reliability of critical structural components." Structure and Infrastructure Engineering, 9(1), 59-77; 2010. ↩ ↩
Wang S, Liu K, Chen C, Chang K. "Experimental investigation on seismic behavior of scoured bridge pier with pile foundation." Earthquake Engineering and Structural Dynamics, 44(6), 849-864; 2015. ↩
Wang X, Ye A, Luo F. "Sesamic response sensitivity analysis of pile supported bridge structures in liquefiable ground." Gongcheng Lixue/Engineering Mechanics; 2016a. (in Chinese) ↩
Wang X, Luo F, Su Z, Ye A. "Efficient finite-element model for seismic response estimation of piles and soils in liquefied and laterally spreading ground considering shear localization." International Journal of Geomechanics, 17(6), 06016039; 2017. ↩
Wang X, Shafieezadeh A, Ye A. "Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground." Bulletin of Earthquake Engineering, 16(1), 229-257; 2018. ↩
Wang X, Ye A, He Z, Shang Y. "Quasi-static cyclic testing of elevated RC pile-cap foundation for bridge structures." Journal of Bridge Engineering, 21(2), 04015042; 2016b. ↩
Wang Z, Dueñas-Osorio L, Padgett J. "Influence of scour effects on the seismic response of reinforced concrete bridges." Engineering Structures, 76, 202-214; 2014. ↩
Zhang J, Huo Y. "Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method." Engineering Structures, 31(8), 1648-1660; 2009. ↩