PDF BibTeX

Comparison and analysis on the new bridge seismic design codes between China and America

YIN Pengcheng (State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092)

Abstract: The design philosophy, design approaches, structure measures, implementation of the regulations and many other aspects of Chinese bridge seismic specifications. , drop behind the Europe and America design specifications. Recent years, the earthquakes through the world bring severe damages to bridges and also accelerate the revising work on bridge seismic design. which has been revised recently is a real set of structure design specifications on the basis of performance requirement. It represents the developing direction of the bridge seismic design specification in the future. Aiming at the revising work of China specifications, this paper has completely compared and analyzed the provisions related to seismic fortification criterion, design methods and flow process between the revising bridge seismic design codes of China and AASHTO. Based on these analyses, some reasonable proposals for the modification are presented.

(Paragraph Translate)本段译文

中国现行的桥梁抗震规范，在设计理念、设计方法、构造措施及规范可执行性等诸多方面均落后于欧美设计规范。近年来，世界范围内发生的地震对桥梁造成了严重破坏，这也加速了桥梁抗震设计规范的修订工作。近期修订完成的《AASHTO桥梁抗震设计指南》是一套真正基于性能要求的结构设计规范，代表了未来桥梁抗震设计规范的发展方向。本文着眼于我国规范的修订工作，全面对比并分析了正在修订中的中国公路桥梁抗震设计规范与《AASHTO桥梁抗震设计指南》在抗震设防标准、设计方法及设计流程等方面的规定。在这些分析的基础上，为我国规范的修订提出了一些合理的建议。

Keywords: bridge; seismic design; code; AASHTO

0. 引言

随着我国90年代经济起飞，交通事业迅猛发展，特别是高速公路的兴建、跨越大江大河的大跨桥梁、大型立交工程以及城市中大量高架桥的兴建，现行的《公路工程抗震设计规范》(JTJ0047-89)已表现出越来越多的不适应性。目前我国正着手制订《公路桥梁抗震设计规范》（现已有征求意见稿，以下简称为《公桥规》），对现有规范做了大量的修订，在抗震设计思想和方法上都对现行规范进行了较大的颠覆。美国是一个多地震的国家，抗震工作开展的较早，且由于地震震害资料比较充分，科学技术高度发达，科研投入幅度较大，工程抗震理论的发展一直走在世界前列，所以从美国规范中汲取经验和先进的研究成果是有着重要意义的。最近美国根据 NCHRP 20-07/Task 193, Task 6 报告修订了规范，出版了《The AASHTO Guide Specifications for LRFD Seismic Bridge Design》（以下简称为《AASHTO》），并即将增补到《AASHTO LRFD Bridge Design Specifications》中。将两本规范进行比较可为《公桥规》的修订工作提供指导，且为下阶段的研究提供参考。

本文根据桥梁抗震设计的基本步骤，从抗震设防标准，抗震体系选择，抗震设计方法，需求和能力的计算和比较以及能力设计等各方面对两本规范进行了全面的比较。

1. 抗震设防标准

抗震设防标准问题是工程抗震设计中需要解决的首要问题。需要通过合理地工程抗震设防，使工程既能有效地减轻地震破坏和损失，又能合理地使用有限的资金。抗震设防标准不仅与设防地震大小有关，而且与桥梁结构的抗震性能要求也是相关的。而抗震性能要求是要通过一定的设计方法以及相应的验算标准来实现的。因此抗震设防标准在整个规范中起到了提纲契领性的作用。

从表1中可以看出，二者对结构的性能目标在基本要求上是一致的，即都把结构在地震事件中不倒塌作为对桥梁结构的最低性能目标。不同的是，《公桥规》采用了两水准设防，并对桥梁的重要性进行了区分，给出了不同的性能目标，且对不同重要性的桥梁的设防等级采用重要性系数 (0.23∼1.7) 来体现。而《AASHTO》由于主要适用于普通桥梁，所以只提出了最低性能标准，对于更高的性能标准以及适用于关键桥梁和重要桥梁的性能目标，则要求业主具体提出。

虽然是单水准，但《AASHTO》通过详细的延性抗震设计和验算以及比我国规范更高的设计地震动水平来保证其性能目标的充分实现，且实际上已将E1阶段即小震不坏的性能要求隐含的包含在其性能目标当中。

表1 抗震设防标准对比

规范	性能目标
公桥规	遭受设计期内发生概率较高的地震影响E1（50年63.2%的超越概率，重现期100年）时，各类桥梁一般不受损坏或者不需修复就可继续使用；遭受设计期内发生概率较低的地震影响E2（50年10%的超越概率，重现期475年）时，A类桥梁一般不受损坏或不需修复可继续使用，B、C类桥梁应保证不致倒塌或产生严重结构损伤，经加固修复后仍可继续使用。D类可倒塌。
AASHTO	对于普通桥梁在75年基准期7%超越概率（1000年重现期）的设计地震作用下要保障生命安全性能目标，即桥梁倒塌的概率很小，但是可能遭受重大的损伤和交通的中断；对于关键桥梁和重要桥梁的可修性或者最小损伤等更高水准的性能应当由业主指定额外的条款。

2. 抗震体系

良好的抗震体系对桥梁的抗震性能是起到决定性作用的。在《公桥规》中没有明确提出抗震体系的概念，只是在动力概念设计中对于塑性铰的布置做了一定的交代。而在《AASHTO》中不仅明确给出了抗震体系，且规定所有抗震设计类别属于SDC C和D即对应于设计地震的基于一秒周期的设计谱加速度系数大于0.3的桥梁及其基础都必须选择一个明确的抗震体系来满足桥梁的生命安全性能要求，这就将桥梁抗震体系的选择作为桥梁抗震设计中的关键环节，突出了抗震体系的作用。

抗震单元是完成抗震体系功能的重要组成部分。《AASHTO》根据业主预期的性能要求将抗震单元分为容许使用；经过业主同意后允许使用以及不建议在新桥上使用三种类型。第一类抗震单元希望把桥梁结构的损伤控制在最小范围，且塑性变形都位于易于检测和修复的位置，可保障桥梁在震后的修复工作以迅速恢复桥梁的通行能力。第二种需向业主协商的抗震单元，塑性变形发生于不容易检测和修复的位置，但仍能有效进行耗能，实际上保证了桥梁震后的有限通行能力。对于第三种不建议使用的抗震单元，这种系统的破坏模式会直接影响到桥梁震后的服务性。

同我国规范相比，《AASHTO》对桩的地下有限延性反应，基础的摇摆和滑动等抗震单元不再简单的规定不允许使用，而是允许在业主的授意下进行更高水平的分析工作来评估单元的性能。即使对可能会影响震后服务性的抗震单元，《AASHTO》也只是不建议在新桥上使用，但同时又规定在不影响桥梁的生命安全性能的情况下，在充分考虑了各种潜在行为模式以及能抑制各种潜在的不被期望的破坏机制，则在业主同意的情况下也允许使用。这就给业主提供了很大的选择空间，充分考虑了业主的需要，即要求业主提供预期的损伤水平，实际上是将由业主来选择可承担的风险水平通过耗能机制和耗能部位的选择过程来得到实现，也就是体现了对桥梁的最优抗震性能即保障震后服务性的考虑，反应了基于性能设计的内涵。

3. 抗震设计方法

由于我国现行规范采用的基于强度的设计方法在设计过程中只进行设计地震作用下的强度验算，未考虑桥梁结构的变形能力和耗能能力，从而导致钢筋混凝土墩柱在强烈地震作用下，往往因设计弯曲延性不足或塑性铰区设计抗剪强度不足而发生破坏。

表2 抗震设计方法对比

规范	设计方法
公桥规	基于位移的设计方法，两阶段设计，E1地震作用下验算强度，E2地震作用下验算强度和变形，采用能力设计方法设计能力保护构件。
AASHTO	基于位移的设计方法，一阶段设计。只在设计地震下验算结构位移，采用能力设计方法设计能力保护构件。

由于强度抗震设计方法的局限性，在设计方法上，《公桥规》采用了与《AASHTO》基本一致的基于位移的设计方法，即都把与以应变为基础的损伤极限状态相联系的位移作为控制结构行为的参数，把位移作为允许结构履行所需功能的地震损伤度量的设计方法。两个规范还通过能力设计方法进行能力保护构件的设计即对主要抗侧力体系构件应用恰当的设计和构造细部设计使之成为强震下的延性耗能机构，其它构件则依据耗能结构的延性确定的强度进行设计。另外，同抗震设防标准相一致，两个规范分别采用的是两阶段设计和一阶段设计。具体对比如表2所示。

4. 抗震设计过程

4.1 抗震设计类别

类似于《公桥规》的烈度分区，《AASHTO》根据全国抗震风险变化进行了抗震设计类别（SDC）的分类。抗震风险水平被定义为地表震动量级的函数，表达为

SD1​=Fv​S1​

，为对应设计地震的基于一秒周期的设计谱加速度系数。表3 AASHTO抗震设计类别要求

SDC	设计要求
A	不需要确定抗震体系；不需要进行需求分析；不需要进行隐性能力检查；不要求进行能力设计；满足支承长度和上下部结构连接设计荷载的最小构造要求
B	不需要确定抗震体系；进行需求分析；进行隐性能力检查；只对墩柱的剪力需求进行能力设计；SDC Ⅱ 水平的构造要求
C	需要确定抗震体系；进行需求分析；进行隐性的能力检查；进行包含墩柱剪力需求的能力设计；SDC Ⅱ 水平的构造要求
D	需要确定抗震体系；进行需求分析；用Pushover分析位移能力；进行包含墩柱剪力需求的能力设计；SDC Ⅱ 水平构造要求

《AASHTO》中每座桥梁都应被指定四种SDC中的一种，详见表3。与《公桥规》类似，《AASHTO》中不同的SDC对应着不同水平的构造措施和抗震措施，但《AASHTO》中对每类SDC还规定了不同的分析方法和设计程序，这是在《公桥规》中所未得到体现的。

4.2 抗震验算指标

由于采用的是位移设计方法，设计的首要问题便是确定位移需求和位移能力。但两本规范在所使用的验算指标上有所区别。如表4所示，《公桥规》对规则桥梁和非规则桥梁规定了不同的验算指标。对于非规则桥梁，在设计地震E2作用下，采用潜在塑性较区域的转角作为位移验算指标。对于规则桥梁，则在设计地震E2作用下采用墩顶位移作为验算指标。当然在本质上墩顶位移还是根据塑性较区的塑性转角以及等效塑性较长度来确定的。而《AASHTO》中，直接采用上部结构质量中心处的位移作为验算指标。另外，除了变形验算，《公桥规》还要进行强度验算，即将地震E1和恒载效应组合后，按现行公路桥涵设计规范有关偏心受压构件规定对构件进行验算。《AASHTO》则对属于不同SDC的桥梁采用不同的验算指标。对于单跨桥和SDC A，《AASHTO》只进行最小支承长度和连接部位的荷载验算。对于SDC B、C、D则要进行位移验算。需要注意的是，对于SDC D，还要增加对于单元延性需求的验算。其中单元延性需求被定义为单元塑性位移需求与理想屈服位移（同理想屈服曲率相关）之和同理想屈服位移的比值。

表4 验算指标对比

规范	验算类型	子类型	验算指标
公桥规	强度验算	抗弯强度验算	地震E1和恒载效应组合后，按现行公路桥涵设计规范有关偏心受压构件的规定进行验算
	变形验算	规则桥梁	墩顶位移：Δ≤Δu​
		非规则桥梁	塑性区纵向和横桥向塑性转动能力：θo​≤θu​
AASHTO	单跨桥	最小支承长度和连接部位的荷载限制	桥跨与桥台在横向和纵向的连接力应大于有效峰值加速度系数A与附属恒载之积；满足最小支承长度要求
	SDC A	最小支承长度和连接部位的荷载限制	A<0.05时，水平设计连接力不小于0.15倍的由附属恒载产生的竖向反应；A>0.05时，水平设计连接力不小于0.25倍的由附属恒载和混凝土产生的竖向反应；满足最小支承长度要求。
	SDC B、C、D	位移需求/能力	ΔtD​≤ΔtC​
	SDC D	单元延性需求	对于单柱框架：μD​≤5；对于多柱框架：μD​≤6；对于墙式墩的弱方向：μD​≤5；对于墙式墩的强方向：μD​≤1

4.3 位移需求计算

确定位移需求时，《公桥规》和《AASHTO》所使用的分析方法是基本一致的，都包含了等效静力法，多模态反应谱法以及时程分析法。但也存在一些差别。《AASHTO》在等效静力法中推荐了两种方法，即均有荷载方法和单模态谱分析方法，而《公桥规》中只包含单模态谱分析方法。《公桥规》中时程分析方法则包含了线性时程分析方法和非线性时程分析方法，而在《AASHTO》中只考虑非线性时程方法。另外，在《公桥规》中还新增补了功率谱方法，这也是《AASHTO》中所没有涉及的。

4.3.1 分析方法选择

在分析方法选择上，《公桥规》和《AASHTO》基本一致，即都需要通过判别桥梁的规则性来确定分析方法。

不同的地方有两点：一是二者对于桥梁规则性的定义不尽相同。二者在跨数，最大圆心角，跨跨间的最大跨长比，跨跨间的排架/墩最大刚度比等指定值上都大体类似，但《公桥规》又增加了对单跨最大跨径，单墩高度与直径或宽度比，轴压比，支座类型，下部结构类型，地基条件等参数的规定。

二是《公桥规》中对分析方法的选择不仅同桥梁的规则性相关，还与桥梁的重要性及所选取的地震作用相关。值得注意的是，《公桥规》规定在A类桥梁和B、C类非规则桥梁中使用时程分析方法，并在设计地震E1作用下采用线性时程分析方法，在E2作用下则采用非线性时程分析方法。另外，对于新加入规范的功率谱方法则规定在A类桥梁和B、C类规则桥梁中使用，其适用范围与多模态反应谱法是基本一致的。

表5 公桥规中桥梁抗震分析方法选择

桥梁类别	规则/非规则	地震E1作用	地震E2作用
A类	规则	-----	TH/MM/SW
	非规则	-----	TH/MM/SW
B类	规则	SM/MM/SW	SM/MM/SW
	非规则	MM/TH	TH
C类	规则	SM/MM/SW	SM/MM/SW
	非规则	MM/TH	TH
D类	规则	SM/MM	-----
	非规则	MM	-----

TH—代表线性和非线性时程计算方法；SM—单模态反应谱方法；MM—多模态反应谱方法；SW—功率谱法。

而《AASHTO》对分析方法的选择则与SDC相关。对SDC A，规范规定不需要进行位移需求分析。对SDC B、C和D，规则桥梁可选用等效静力方法或多模态反应谱方法，而不规则桥梁则只能使用多模态反应谱方法。由于《AASHTO》主要适用于普通桥梁，规范规定非线性时程分析应用于SDC D中使用隔震装置和能量耗散装置的桥梁以及几何形式较为复杂或临近断层的桥梁。对某些被确定为关键或重要的桥梁，应经业主同意后使用非线性时程分析方法。

4.3.2 多模态反应谱计算

进行分析方法选择后，就要根据选定的计算方法来进行位移需求的计算。从表6中可以看出，对于《公桥规》和《AASHTO》主要使用的多模态反应谱分析方法，二者都是根据等位移原理来进行位移需求的计算，且在计算中都考虑了阻尼修正，方向组合以及竖向地震动的影响。

另外，由于使用的是等位移原则，对预期以非弹性形式反应的短周期结构会产生较大偏差，所以《AASHTO》通过位移放大系数

Rd​

对短周期结构的位移计算结果作了相应的调整。在《公桥规》中则没有进行相应的考虑。但在《公桥规》中，反应谱最大适用周期为10s，考虑了长周期反应谱，这比《AASHTO》中的适用周期要长的多。表6 多模态反应谱计算对比

项目	公桥规	AASHTO
阻尼修正	用阻尼调整系数C0修正设计反应谱	直接对反应谱计算结果使用阻尼折减系数Rp
质量参与系数	纵向和横桥向获得90%的质量参与系数	纵向和横桥向获得90%的质量参与系数
短周期调整	位移放大系数Rp调整	无
模态组合	SRSS：对两个振动模态的自振周期接近时，CQC	CQC
竖向地震动	设防烈度为8度和9度时的拱式结构、长悬臂结构和大跨度结构，考虑竖向地震作用，由水平分量的设计加速度反应谱乘以规范给出的修正谱系数得出竖向分量的设计加速度反应谱	一：对于断层6英里内的普通桥梁，当桥梁场地基岩峰值加速度大于0.5g时，对上部结构均匀施加2.5%的加载大小的竖直向上和向下的等效静力荷载以评估竖向地震度影响。二：对于长的，柔性的，在竖向荷载的传力路径上存在其他形式大偏心的桥梁，直接在时程分析中包含竖向地震动。
方向组合	30%法则：Ex+0.3Ey+0.3Ez；0.3Ex+0.3Ey+Ez；0.3Ex+Ey+0.3Ez；	30%法则：Ex+0.3Ey+Ez；0.3Ex+Ey+Ez；

4.4 位移能力计算

两本规范中，位移能力都是和材料的应变极限状态相关的。但在位移能力的具体计算方法上二者是有差别的。如表7所示，在《公桥规》中，位移能力的计算是同桥梁的规则性相关的。对于非规则桥梁，由于使用塑性铰区的塑性转角作为验算指标，所以计算的位移能力也就是计算塑性铰区的最大容许转角。对于规则桥梁，位移能力为桥墩墩顶的容许位移。另外在规则桥梁中，单柱墩和多柱墩的位移能力确定方法也不相同。

表7 公桥规位移能力确定方法

桥梁类型	墩类型	位移能力确定方法
规则	单柱墩	Δu​=31​H2ϕv​+(H−0.5Lp​)Kp​(ϕu​−ϕv​)
	双柱墩，排架墩	纵桥向与单柱墩相同，横桥向要求在盖梁处施加水平力进行非线性静力分析。墩柱塑性铰达到容许转动能力时的盖梁处横向水平位移为容许位移。
非规则	-	ϕp​=ϕu​−ϕv​, ϕu​=KLp​ϕp​​，ϕu​为截面屈服曲率，ϕy​为极限破坏状态的曲率能力，K为安全系数，L为等效塑性铰长度。

如表8所示，在《AASHTO》中，位移能力的计算是与SDC相关的。对于在SDC B和C中属于抗震设计策略一型的即预期反应形式为上部结构完全弹性下部结构延性的结构，每个排架的位移能力是根据近似公式来确定的。对于不满足等式要求及不属于一型抗震设计策略的结构，则通过满足更高的SDC的构造要求来增加允许位移能力或调整桥梁动力特性的方式来满足等式要求。对于SDC D，则需要使用非线性静力分析，即使用pushover分析来确定结构达到稳定性极限时可靠的位移能力。

表8 AASHTO位移能力确定方法

SDC	抗震设计策略	位移能力计算	注释
B	一型	ΔC​=0.12H⋅(−1.27ln(x)−0.32)≥0.12H	x=ΔBo​/H
	不满足等式要求或者不是1型结构	满足更高SDC构造要求来增加允许位移能力或调整桥梁动力特性以满足等式
C	一型	ΔC​=0.12H⋅(−2.32ln(x)−1.22)≥0.12H	Ho=墩柱的净高度 Bo=墩柱直径或者考虑中的平行于位移方向所测量的宽度 Δ=墩柱端部限制条件因子
	不满足等式要求或者不是1型结构	满足更高SDC构造要求来增加允许位移能力或调整桥梁动力特性以满足等式
D	-	pushover分析

还有一点需要注意的是，《AASHTO》在进行位移能力确定时，对SDC C和D考虑了

P−Δ

效应的影响，对SDC B则不考虑

P−Δ

效应。在SDC C和D内属于一型抗震设计策略结构中，当

Pdl​Δl​≤0.25Ml​

时，即施加于柱上的重力荷载与柱的反弯点和塑性铰最远端间的相对侧向偏移之积不大于0.25倍的基于期望材料性质的钢筋混凝土墩柱的名义弯矩能力时，可以忽略

P−Δ

效应。若不能满足该要求，则需要通过调整桥梁的动力特征以满足上述要求达到忽略

P−Δ

效应的目的。这些要求在《公桥规》中都没有进行考虑。

4.5 需求/能力比较

在得到了位移需求和位移能力之后，就可以进行需求和能力的比较。在《公桥规》中，如果不能满足位移需求小于位移能力的要求，则要进行重新设计。但没有给出具体的重新设计的细节。而在《AASHTO》中，则做了较为详细的规定。如前所述，桥梁首先应当根据场地地震风险被归类为抗震设计类别中的一种。对于SDC A和单跨桥是不需要进行位移分析的。对余下的SDC B、C和D，则根据相应的抗震设计类别进行位移需求和位移能力计算。当无法满足位移需求小于位移能力的要求时，则提高抗震设计类别，通过提高相应的构造要求水平来提高结构的位移能力，若仍不能满足要求，则继续提高直至SDC D。如果还是无法满足位移需求小于位移能力的要求，则调整桥梁的动力特性，并继续在SDC D下验证结构的位移要求，直至验算通过为止。具体流程可参看图1。

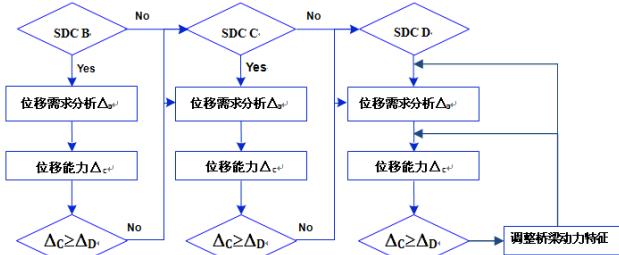
在《AASHTO》中，动力特性的调整包括了对超大型管桩的应用；调整有效桩长（如降低基脚、采用隔离套管等）；使用修正的端部固定；减少/重新分配上部结构的质量；改变柱的截面和纵向配筋率；增加或者重新定位墩柱；调整铰/伸缩缝的位置；引入隔震支座或阻尼器（反应调节装置）；重新设计连接等诸多措施。

4.6 能力保护设计

4.6.1 超强系数

由于抗剪验算和能力保护构件的设计都要根据考虑了结构超强的塑性铰处的弯矩能力来进行计算，所以在进行能力保护设计前，首先要确定超强弯矩的取值。在《公桥规》和《AASHTO》中，超强弯矩能力都是通过超强系数与墩柱的塑性弯矩能力的乘积来确定的。但是二者关于超强系数和塑性弯矩能力的取法都是不同的。在《公桥规》中，超强系数统一的取为1.2。在《AASHTO》中，对于钢筋混凝土墩柱，超强系数根据使用的钢筋不同而有所区别。对于ASTM A706钢筋，超强系数取为1.2。对于ASTM A615 Grade60钢筋，超强系数则取为1.4。

另外，在《公桥规》中规定塑性弯矩能力根据可能出现的塑性铰处按安配钢筋，采用材料标准强度值和相应轴压力计算。在《AASHTO》中则是通过基于期望的材料特性的弯矩-曲率（

M−ϕ

）分析来计算。通过把

M−ϕ

曲线理想化为完全弹塑性曲线，使理想化曲线的弹性部分通过

M−ϕ

曲线上标志第一根钢筋屈服的点，并使可以通过第一根钢筋屈服点后的真实

M−ϕ

曲线与理想化完全弹塑性曲线所包围的面积相等的原则来确定理想化的塑性弯曲能力。

4.6.2 抗剪验算

确定了超强弯矩，就可以利用超强弯矩来确定墩柱剪力需求和能力保护构件的设计荷载。《公桥规》和《AASHTO》对于墩柱抗剪设计的要求同样是通过计算墩柱的剪力需求和能力并进行比较来实现的。

如表9所示，在《公桥规》中，剪力需求取为按能力设计方法计算的同超强弯矩相关的沿纵桥向或横桥向的剪力设计值和地震E2作用下得到的纵向或横向剪力中的较小者。

表9 墩柱抗剪能力计算对比

贡献	规范	公式	注释
钢筋	公桥规	Vx​=0.1Ak​bRg​	fC​为混凝土圆柱体抗压强度；A为核芯混凝土的面积；A为截面上箍筋总面积；S为箍筋间距(cm)；R为箍筋抗拉设计值；b为沿计算方向的墩柱宽度；
		Vx​≤0.67fC​​A
	AASHTO	螺旋或环形箍筋：Vx​=2π​(nAp,fy​Ds​)	A为螺旋或环形箍筋面积；fC​为箍筋的屈服应力；D为柱核心的直径；B为矩形柱的宽度；S为箍筋或系筋间距；A为荷载方向的箍筋面积；d为荷载方向截面有效深度；Ae​为单元毛截面面积；Pc​为截面上的极限压力；D为螺旋或环形箍筋直径；fC​为混凝土名义抗压强度；μ为单元的最大位移延性率；
		矩形箍筋：Vx​=sAfyk​d​
		Vx​≤0.25fC​​A
混凝土	公桥规	Vc​=0.0023×fC​​×Ae​
	AASHTO	Vc​=νc​Ae​	Ae​=0.8Ae​
		νc​=0.032α′(1+2As​Pd​​)	对螺旋或者环形箍筋：0.3≤α′=0.15+3.67−μD​fC​​≤3, ρy,fy​fC​​≤0.35, ρy​=sD4Ae​​
			对矩形箍筋：0.3≤α′=0.15+3.67−μD​fC​​≤3, 2ρy,fy​fC​​≤0.35, ρy​=sD4Ae​​
			μD​=ρy,fy​≤0.35, ρy​=sD4Ae​​
			μD​=2ρy,fy​≤0.35, ρy​=sD4Ae​​

与《公桥规》不同，《AASHTO》的剪力需求的计算是同抗震设计类别相关的。对于SDC B，墩柱的剪力需求取为线弹性地震分析获得的内力以及同墩柱塑性铰相关的包含超强系数的内力中的较小值。对于SDC C和D，则直接取为同超强弯矩相关的剪力。

至于抗剪能力，《公桥规》和《AASHTO》都考虑了混凝土和箍筋对抗剪的共同贡献，如表9所示。

当确定箍筋对于墩柱的抗剪能力贡献时，两个规范给出的公式的基本形式是一致的，且为了保证界面内的混凝土在箍筋屈服前不至于被压碎，两个规范都给定了最大抗剪钢筋的取值。《公桥规》中取了0.25的系数，而《AASHTO》中取了0.67的系数，这可能与二者对于墩柱有效抗剪面积以及混凝土的抗压强度的取值不同是相关的。在确定混凝土的抗剪能力时，由于混凝土剪切强度在塑性铰区域内随着延性需求的增加而退化，且随着横向约束的加强而增加，《AASHTO》通过系数

α

考虑了构件的局部延性能力以及箍筋的含箍率对混凝土剪切能力的影响。对SDC B，

μD​

取为2；对SDC C，

μD​

取为3；而对SDC D，则根据规范给定公式，按单元的塑性位移需求与理想屈服位移（同理想屈服曲率相关）之和同理想屈服位移的比值来得到。得出墩柱的抗剪需求和抗剪能力后，就需要进行需求和能力的比较。两个规范都通过抗剪强度折减系数

ΦS​

考虑了对抗剪能力的折减，即

ΦS​Vn​≥Vu​

的形式。

4.6.3 能力保护构件设计和构造措施

能力保护构件主要包括基础，盖梁以及墩柱与基础和盖梁的节点。能力保护构件的设计荷载也是根据超强弯矩计算的。其中对于基础的抗震设计，在《AASHTO》中提供了详细的桥梁基础抗震设计条文，而《公桥规》在这个方面仍处于一片空白，基础的抗震设计仍然是沿用静力设计方法；至于构造措施，虽然相比于现行规范，《公桥规》做了一定的修订，但通过两本规范的对比，显然《AASHTO》的构造细节要求更为细致，箍筋和纵筋的构造要求不仅同抗震设计类别相关，且在塑性铰区域内和塑性铰区域外还考虑不同的构造措施，可保证桥梁结构的延性能够得到充分发挥。另外《AASHTO》对纵筋的搭接和锚固要求也进行了更加详尽的规定。限于篇幅，关于这几点的详细对比在本文中不再作详细讨论。

5. 结语

近十几年发生在世界各地的大地震给桥梁结构造成了重大破坏，同时也促进了桥梁抗震设计规范的修订工作。应该说经过修订的《公桥规》已在很多方面借鉴和吸收了近来的地震震害经验以及现代抗震研究领域的最新研究成果，但仍在很多方面与美国规范有着一定的差距，故提出以下建议：

（1）​抗震设防标准​。这是桥梁抗震设计中的基本问题。同现行规范相比，《公桥规》提出了明确的性能目标，即满足“小震不坏，大震不倒”。但同《AASHTO》相比，《公桥规》的设防地震水平还是偏低，这可能同我国的经济发展水平是相关的。但是今年发生的汶川大地震显示出在设防地震动水平的确定上仍存在一定的问题。这就需要对合理的抗震设防标准进行进一步的研究。

（2）​抗震体系​。良好的抗震体系能提供良好的抗震性能和抗震整体性。在规范中给定合理的抗震体系对工程师的抗震设计是具有良好的指导作用的。

（3）​抗震单元​。我国的抗震单元仍只局限于墩柱塑性铰以及隔震支座，以期使结构的损伤都处于易发现和检修的部位。但是在很多情况下，这种目标的实现是相当困难和耗资巨大的。AASHTO将抗震单元分为了允许，经业主同意后允许和不建议三类，将桩的有限延性反应，桥台的抗力作用等以前在抗震设计中不希望出现的反应引入了抗震单元的定义，给予了业主充分的选择权，体现了对桥梁的最优抗震性能也就是保障震后服务性的考虑，反应了基于性能设计的内涵。这一点是值得我国规范充分借鉴的。

（4）​抗震设计类别​。我国规范根据地震风险按照度对结构进行了分区，并对不同烈度区的桥梁提供不同的抗震措施。但这种做法是不具有设计上的连续性的。应当借鉴《AASHTO》中，对具有不同抗震风险的桥梁，不仅提供不同水平的抗震措施，还要提供不同的设计水平，从设计层面就保证了具有不同风险水平桥梁的性能。

（5）​反应谱的短周期调整​。由于反应谱计算中使用的是等位移原则，对预期以非弹性形式反应的短周期结构会产生较大的偏差。所以应该在反应谱计算中考虑短周期调整。

（6）​动力特性调整​。确定位移需求/能力比后，当不满足要求时应给出具体的动力特性调整的措施。应当尽可能加强条文的可操作性，给予工程师更多的设计细节和正确的指导。

（7）​超强系数​。超强概念是随着能力设计原理的提出和发展而逐渐被认识的。设计中一般希望能力保护构件中发生弹性反应，故必须充分估计塑性铰区截面的超强现象，即要确定合适的超强系数，否则，按能力设计原则进行抗震设计的有效性将大大降低。应对超强系数的取值进行更为深入的研究，考虑超强系数的各种影响因素。

（8）​桥梁基础的抗震设计​。从历次大地震震害可以看出，基础破坏是导致桥梁结构地震破坏的主要原因。应当给予基础的抗震设计足够的重视，制定相关的抗震条文。

（9）​构造措施​。仅仅依靠定量计算还不能完全解决桥梁结构抗震设计中的许多问题。应当汲取美国规范的经验，制定更为细致的构造细节要求，保证桥梁结构的延性能够得到充分发挥。

参考文献

[1] AASHTO Guide Specifications for LRFD Seismic Bridge Design, Subcommittee for Seismic Effects on Bridges T- 3, 2007
[2] AASHTO.2007. LRFD Bridge Design Specifications, 4th Ed., American Association of State Highway and Transportation Officials, Washington, DC.
[3] Caltrans seismic design criteria. version 1.4[S].
[4] ATC- 32, Improved Seismic Design Criteria for California Bridge: Provisional Recommendations[R]. California: Applied Technology Council(ATC),1996.
[5] NCHRP 12- 49 (2001). Recommended LRFD Guidelines for the Seismic Design of Highway Bridges, Part I: Specifications and Part II: Commentary and Appendixes, NCHRP 12- 49 Project Team, MCEER, State University of New York at Buffalo, Buffalo, NY.
[6] JTJ 004- 89. 中华人民共和国交通部部标准:公路工程抗震设计规范[S].
[7] 公路桥梁抗震设计规范（征求意见稿）.
[8] 范立础, 胡世德. 叶爱君. 大跨度桥梁抗震设计. 人民交通出版社, 2001.
[9] 范立础, 王君杰. 桥梁抗震设计规范的现状与发展趋势. 地震工程与工程振动, 2001,21(3):70~77
[10] M.J.N.普瑞斯特雷等著, 袁万诚等译. 桥梁抗震与加固. 北京: 人民交通出版社, 1997.
[11] 叶爱君. 桥梁抗震人民交通出版社, 2002.