1 引言

桥梁抗震区别于一般建筑结构物抗震的一个显著特征是: 如果在地震中桥梁工程遭到严重破坏, 切断了震区交通生命线, 将会造成救灾工作的巨大困难, 使次生灾害加重, 导致巨大的经济损失。随着现代化城市人口的大量聚集和经济的高速发展, 对交通线的依赖性越来越强, 而一旦地震使交通线遭到破坏, 可能导致的生命财产以及间接经济损失也将会越来越巨大。几次大地震一再说明了桥梁工程遭到破坏的严重后果, 也一再说明对桥梁工程进行抗震设防的重要性。

目前, 国内外公认的减轻地震灾害的最有效措施是对工程结构进行合理而又经济的抗震设防。如何合理地进行工程抗震设防, 使其既能有效地减轻工程的地震破坏和损失, 又能合理地使用有限的资金, 就成为工程抗震设计中需要解决的首要问题。这就是抗震设防标准问题。所谓工程抗震设防标准是指根据地震动背景, 为保证工程结构在寿命期内的地震损失不超过规定的水平或社会可接受的水平, 规定工程结构必须具备的抗震能力。

谢礼立²等认为: 决定工程抗震设防标准的因素有三个, 即社会经济状况、地震危险性和工程结构的重要性。确定工程抗震设防标准时, 需要综合考虑工程的设防原则、设防目标、设防环境、设防参数、设防水准、设防等级。确定最优设防标准的核心问题是正确地解决设防标准与设防原则及目标之间的关系。这种关系可以被抽象为一个多变量、多目标、多约束的动态最优决策问题。对一般结构和工程的设防标准建立决策模型时, 模型中的基本变量应当是抗震设防水准, 目标函数应力求最大限度地反映设防原则和目标的要求, 使为减灾目的的防灾投入与采取措施后的潜在地震损失之和为最小。桥梁抗震设防标准包含两方面的内容: 抗震设防水准和相对应的抗震性能目标。

大型桥梁工程的投资大, 在交通网络中所处的地位重要, 一旦受损后修复的难度也大, 而造成的经济损失更是难以估计, 因此目前, 大型桥梁工程具体采用的抗震设防标准, 一般由业主参考其他大型桥梁工程已采用的抗震设防标准, 并根据工程的重要性、自身的经济能力以及所能承受的风险水平, 进行决策并报批。针对大型桥梁工程, 由于其所处区域的地震危险性、社会经济状况和其在交通网络中的重要性具有其个体的特殊性; 其抗震设防标准需要进行单独的量化的研究。

2 桥梁工程抗震设防标准的总体思路

2.1 最优决策模型的目标函数

最优决策就是要从所有可能的方案中找出最满意的方案, 即在满足约束条件的情况下使得目标函数取最佳值的方案。因此, 最优决策模型中目标函数的确定是一个十分重要的问题。

在抗震设防标准的最优决策模型中, 目标函数应当最大限度地反映设防原则和设防目标的要求, 一般说来目标函数可以是: ① 期望的总损失取最小; ② 工程造价取最小; ③ 抗震设防后的长远效益取最大。

抗震设防标准决策模型的合理目标函数应该是使按某一地震重现期(T_R 或其它地震动参数)建造的工程结构的抗震投入与该结构在各种不同重现期地震作用下的期望损失之和为最小, 才能在地震作用下的损失和抗震投入之间取得最佳平衡, 从而确定合理的抗震设防标准。因此, 抗震设防标准最优决策模型的目标函数可用下列公式表示:

式中: T_R 为地震重现期;

S(T_R) 为某桥按 T_R 设防的结构抗震投入与该桥在各种可能发生的重现期地震作用下的期望损失之和;

C(T_R) 为该桥以 T_R 作为设防地震重现期的工程造价与不设防时结构的初始造价之差, 即工程结构为抗震设防所增加的投入, 简称为结构抗震投入, 是地震重现期 T_R 的增函数;

L_P(T_R) 为该桥以 T_R 作为设防地震重现期时, 总损失的期望值, 是 T_R 的减函数;

P(T_R) 为该桥址 T_R 的发生概率, 由地震危险性分析结果给出;

L(T_R) 为该桥以 T_R 作为设防地震重现期时, 各种可能发生的重现期地震作用下的损失(包括直接损失、间接损失)。

由上式可得出最优设防地震重现期的决策图, 如图1所示。其中, T_R^* 为 S(T_R) 最小值处所对应的最优设防地震重现期。

对于桥梁工程, 抗震设防标准的科学决策非常困难, 因为桥梁工程的 L(T_R) 中的间接损失的不确定性, 所以定量的地震损失分析比房屋结构要困难得多。

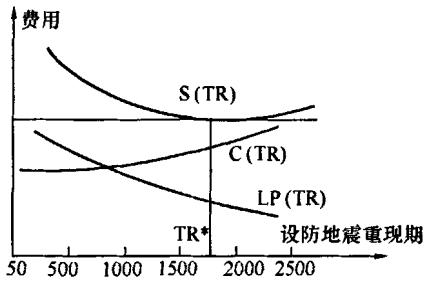
图1 决策模型示意图

2.2 最优决策模型的约束条件

严格说来, 凡目标函数未能反映的设防原则和设防目标都应当作为决策模型的约束条件。但由于数学处理上的困难, 这往往是不可能的, 但是下列约束条件必须加以考虑:

(1) 确保地震后的人员伤亡数、政治影响不超过社会可接受的水平;

(2) 根据结构的使用功能, 实现其性能要求。应保证抗震设计规范JTJ044—89所规定的"小震不坏、中震可修、大震不倒"的多级设防的思想和原则得到体现和贯彻。

2.3 最优决策的数学模型和分析框图

抗震设防标准的最优决策应该使按某一设防地震重现期建造的桥梁结构的抗震投入与该结构在各种不同重现期地震作用下的期望损失之和为最小, 目标函数取最小值在数学上相当于求解下式:

满足上式的设防地震重现期对应的就是最合理的设防地震重现期, 即最优的设防地震重现期 T_R^*。由于抗震设防投入 C(T_R) 随设防地震重现期 T_R 的增加而增加, 但所造成的地震损失 L_P(T_R) 却随设防地震重现期 T_R 的增加而减小, 因而存在一个使总费用 S(T_R) 为最小的最佳设防地震重现期 T_R^*。

由上述分析可知, 抗震设防最优设防地震重现期的确定本质上是一个以减轻地震灾害损失、减少抗震设防投入为主要目标的多约束最优决策问题。决策时需要解决的主要问题有: 1) 某地区设防地震重现期发生概率的确定; 2) 结构破坏概率的确定; 3) 地震预期经济损失; 4) 抗震设防投入及工程造价分析。设防标准决策分析框图见图2。

2.4 经济最优设防地震重现期的决策分析

所谓"经济最优设防地震重现期"是指不考虑人员伤亡和社会影响问题, 仅满足抗震投入与经济损失的和 S(T_R)=C(T_R)+L_P(T_R) \to \min 所求得的地震参数。而最优设防地震重现期则是指一方面满足投入与经济损失的和为最小, 另一方面满足"人员伤亡、交通瘫痪导致的救灾迟缓满足社会可接受的水平"这一约束条件时所确定的设防地震参数。

因为人员伤亡和社会影响的复杂性, 我们一般采用在获得经济最优设防地震重现期后, 再用人员伤亡和社会影响进行修正来优化设防地震重现期, 从而使得最优设防地震重现期成为一个可解的数学模型。

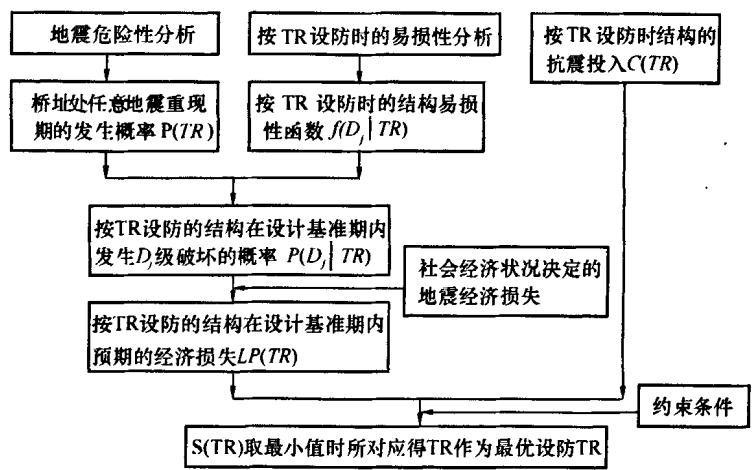
图2 设防标准决策分析框图

3 桥梁工程抗震设防标准基本环节决策流程

3.1 地震危险性曲线及危险性特征研究

地震危险性是指某一场地在一定时期内可能遭受到的地震作用的大小和频次, 可用烈度、地震动参数或地震重现期来表示。对未来某个地区中将要遭遇地震动重现期的大小、或不同地震动水平重现期的概率、或超过给定地震动重现期水平的概率进行预测估计的工作, 叫做地震危险性分析。

地震危险性分析的结果: 地震危险性曲线——烈度、地震重现期或其它地震动参数的超越概率 P(T \ge T_R), 画出危险性曲线。

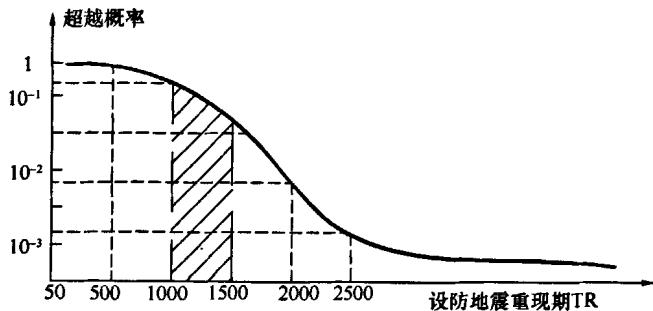
图3 设防地震重现期超越概率曲线

3.2 抗震设防标准研究中的地震易损性分析

(1) 地震易损性分析的基本概念

结构的地震易损性是指结构在地震作用下, 发生某种破坏程度的概率或可能性。易损性可采用从0(无破坏)到1(完全破坏)的标量形式来表达。

(2) 破坏程度——震害等级划分

破坏程度实际上是一个连续函数, 但是因为对于破坏程度的定量研究目前还没有很好的方法, 这也成为易损性研究的难点。所以大多将破坏程度简化为破坏等级; 而破坏等级划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌五个等级。

各级破坏的宏观划分标准如下:

1. 基本完好(含完好): 承重构件完好, 个别非承重构件轻微破坏, 附属构件有不同程度的破坏, 不加修理可继续使用。
2. 轻微破坏: 个别承重构件出现可见裂缝, 个别非承重构件有明显裂缝, 附属构件有不同程度的破坏, 不需要修理或稍加修理即可继续使用。
3. 中等破坏: 多数承重构件出现轻微裂缝, 部分有明显裂缝, 个别非承重构件破坏严重, 需要一般修理。
4. 严重破坏: 多数承重构件严重破坏, 或有局部倒塌, 需要大修, 个别桥梁修复困难。
5. 倒塌: 多数承重构件严重破坏, 结构濒于崩溃或已倒毁, 已无修复可能。

上面的描述中, 模糊量词的大致范围是: "多数"指 50% 以上, "部分"指 30% 以下, "个别"指 5% 以下。

在本文中, 我们采用符号 D_j 来表示第 j 级震害等级, 即:

(3) 易损性分析的结果

易损性函数 f(D_j \mid T_R): 表示在地震重现期 T_R 的条件下, 破坏等级 D_j 的连续概率函数, 表示了结构的易损性。

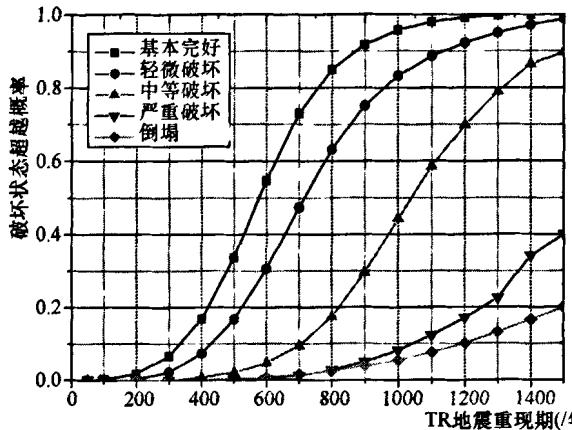
图4 易损性函数曲线

3.3 设防标准研究中的结构破坏概率

根据地震危险性分析和易损性分析的结果得出:

按 T_R 设防的结构在设计基准期内发生 D_j 级破坏的概率 P(D_j \mid T_R):

3.4 设防标准研究中的地震经济损失估计

在地震经济损失分析中, 区别于房屋建筑, 间接经济损失在桥梁中处于主要地位。为了简化模型, 在本文中桥梁的地震经济间接损失主要用经济效果来评估。桥梁的间接经济损失主要是由其在交通网络中的重要性决定的。桥梁相当于交通网络中的节点, 如果因为震害导致交通中断, 即交通网络中的某节点不能通行; 交通必然通过其他网络节点进行疏通, 由此产生的附加费用为地震经济损失的间接经济损失主要部分。如桥梁为通向某灾区的唯一关键节点, 则其在交通网络中处于最关键的地位, 决定着整个交通网络的通行, 无疑客观上要求大大提高此桥的抗震设防标准。

桥梁的地震经济损失中的间接经济损失主要体现为:

1. 增加的运输成本费。
   因为震害导致的桥梁交通的中断, 从而导致车辆必须绕行, 从而增加的运输费用。
   包括燃料、轮胎、保养护理、车辆折旧等, 这些与道路状况及行车里程有关。
2. 增加的运输时间。
   因为震害导致的桥梁交通的中断, 从而导致车辆必须绕行, 从而增加的运输时间。
   时间费用的计算方法是先算出改道绕行而增加的行驶时间, 然后把时间换算成货币价值。车辆乘员及旅客的时间应区别出工作时间和非工作时间。前者用一个人的平均工资计算, 后者用本人所得时间价值评估。为此选用有关单位以往的调查结果。非工作时间的价值, 约取平均工资的 25% 。从各种车辆平均工作时间、非工作时间的比例和旅客人数得出一辆车平均时间价值, 计算时间效益。时间价值通常按一定的增长率, 增长率取决于国民经济的发展水平。运输时间增加为各种损失中的主要部分。
3. 因为交通中断导致的受灾区域经济损失
   因为交通不便, 导致的企业的经济损失以及整个区域的GDP损失。

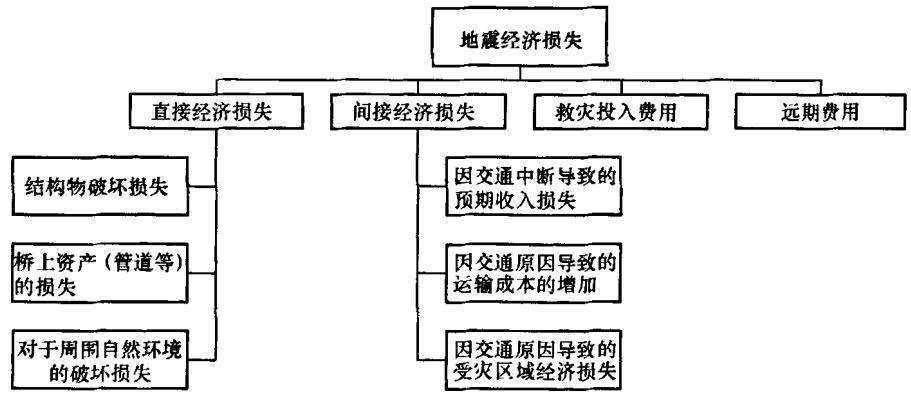
可见, 桥梁的地震经济损失中的间接经济损失涉及范围很广, 难于精确估计, 此点也构成了整个决策流程的难点。

3.5 经济最优设防地震重现期的决策分析

根据工程概预算结果得到按 T_R 设防时结构的工程抗震投入 C(T_R); 结合3.4得到的按 T_R 设防的结构在设计基准期内预期的经济损失 L_P(T_R), 即可按照下式得到经济最优设防地震重现期:

3.6 考虑约束条件的最优设防地震重现期的决策分析

在抗震设防标准的研究中, 人员伤亡和社会影响是评价设防标准无法回避而又难以解决的问题。从研究抗震设防标准的角度来看, 研究人员伤亡估计方法的目的在于探究设防标准的高、低对地震死亡数量的影响, 及如何确定合理的设防标准来控制地震的死亡数量两方面。因此在抗震设防标准的研究中, 人员伤亡和社会影响的期望结果是: 得到适合于制定设防标准用的利用不同破坏状态与人员死伤率的关系、结构易损性分析结果及地震危险性分析的结果的估算人员伤亡期望值的公式。然后依照此结果来修正所得到的经济最优设防地震重现期。

结语

大型桥梁工程抗震设防标准的科学决策是一个非常复杂的问题, 还需要进行大量的研究工作。而其关键在于桥梁在交通网络中的重要性所决定的桥梁的性能目标。而某个大型桥梁工程具体采用的抗震设防标准, 应高于最低设防标准, 由业主根据工程的重要性、自身的经济能力以及所能承受的风险水平, 按照上述流程来进行决策。

参考文献